随着我国社会经济的发展，电力需求持续增长，清洁低碳成为我国能源转型发展的重要特征.如何在保证电力系统安全、稳定运行的同时，最大程度地消纳各种清洁能源成为当前电网转型发展亟待解决的问题[1].与传统的被动式运营管理配电网相比，主动配电网可以充分利用各种先进信息与管理技术，实现对分布式能源灵活有效的控制[2-3].
主动配电网的优化控制是实现可再生能源消纳的关键技术，国内外学者对此开展了广泛的研究[4-6].刘东等[7]提出了主动配电网分层能量管理体系，该方案在上层控制区域信息交互的基础上，利用功率扰动预测信息，结合下层电网的运行状态信息，实现了不同控制模式之间的主动切换；戴志辉等[8]提出了“微网
配网”两步控制策略，采用粒子群算法对含有多微网的主动配电网进行仿真分析，有效降低了对上级电网的依赖；谢文强等[9]基于虚拟电压和自律分散控制的思想，以动态跟踪各母线换流器出口电压的方式实现了微电网的均流控制；王琛等[10]使用分散控制和集中控制相结合的方式，避免微网中蓄电池的深度充放电过程，并实现了对电能质量的改善；侯文庭等[11]在已有的核电运行经验基础上，采用阶段调度方法，将核电引入配网的优化运行中，解决了风电、光伏出力不确定性问题.
目前关于主动配电网的优化控制研究多是基于能量管理系统的角度，较少涉及主动配电网供需两侧的组合优化问题[12-13].本文针对主动配电网的多源协同问题，充分考虑可再生能源以及负荷需求，构建了以节约系统调度成本、提升可再生能源利用率及提高用户满意度为目标的多源协同主动配电网优化调度模型.利用改进微分进化算法对模型进行求解，实现了对各类资源的有效利用.
1 多源协同优化模型
1.1 配电网模型
主动配电网中分布式电源的出力预测与负荷预测是实现对其优化控制的基础，因此首先建立了包含风力发电、光伏发电、电动汽车动态充放电等多种电源的配电网模型.
由统计数据可知，风力发电机的输出功率与风速之间关系式[14-15]为
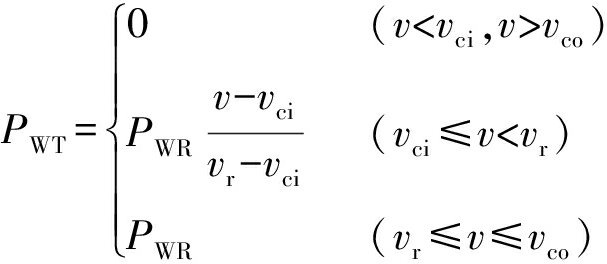
（1）
式中：PWT为风力发电机的实际输出功率；PWR为风机的最大功率；v、vci、vco、vr分别为风机所处位置的风速、切入风速、切出风速与额定风速.
光伏发电输出功率表达式[16]为
PM=ARη
（2）
式中：PM为光伏发电输出功率；R为光照强度；A为方阵面积；η为光电转换效率.
电动汽车的日行驶里程md服从对数正态分布，其概率密度函数表达式为
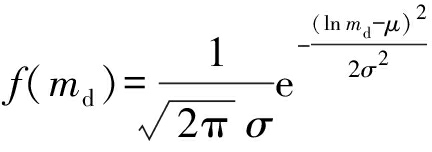
（3）
电动汽车充电时间与离网时间的概率密度函数表达式为
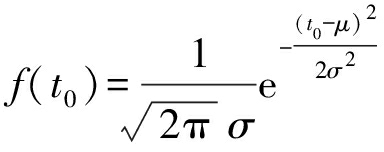
（4）
（5）
式中，t0、t1分别为电动汽车接入电网时间与脱离电网时间.计算过程中，通过计算机产生随机数的方法模拟电动汽车的充放电行为.
负荷概率密度函数可用正态分布表示为
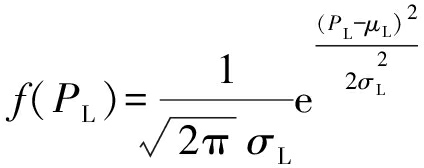
（6）
式中：PL为负荷功率；μL为负荷功率期望；σL为负荷功率标准差.则负荷的累计分布函数为
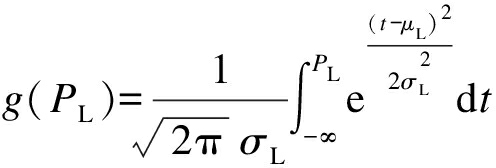
（7）
1.2 优化调度模型
文中从配网调度的经济性、清洁能源的利用率及用户满意度三个方面，建立了多源协同的主动配电网优化控制模型，在满足系统功率平衡约束条件下，采用改进的微分进化算法对其进行求解.
1） 调度的经济性.主动配电网运行总成本主要由调度成本C1、购电成本C2、分布式电源运维成本C3，清洁能源发电补贴C4与电动汽车充电收入C5构成，其表达式为
C0=C1+C2+C3-（C4+C5）
（8）
除去成本外，配电网向用户售电的总收益F表示为
（9）
式中：PL，t为主动配电网在t时刻的负荷；CEX，t为当前时刻的电价；Sum为统计周期的总数.则关于调度成本的目标函数表达式为
（10）
2） 清洁能源利用率.定义清洁能源利用率为调度周期内清洁能源的消纳量占其发电出力的比例，则清洁能源利用率表达式为
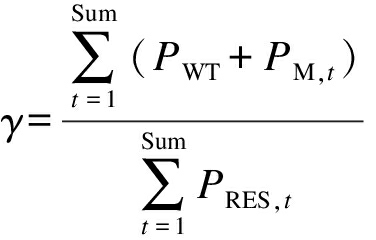
（11）
式中，PRES，t为t时刻清洁能源的总发电功率.则目标函数可表示为
max f2=γ
（12）
3） 用户满意度.用户满意度属于用户的一种用电体验，为对其进行量化衡量，本文从用户用电时间β1、用电量β2及电动汽车的荷电状态β3构建的满意度函数为
max f3=β1+β2+β3
（13）
其中，β1、β2、β3分别表示为
（14）
式中：S1、S2分别为削减负荷、可转移负荷参与调度的时间段；ΔQD，t、QDT，t为可削减负荷在t时刻的削减量和总用电量；ΔQS，t、QST，t为可转移负荷在t时刻内的转移量与总用电量.
（15）
式中：Us为用户总数；ΔTD，y、TDT，y为可削减负荷用户y的负荷削减时间和可削减总时间；ΔTS，y、TST，y为可转移负荷用户y的负荷转移时间与可转移总时间.
（16）
式中：NEV为电动汽车总数；SocE，y、SocB，y分别为汽车现有电量与满电量.
综合目标函数f1、f2、f3，则总的目标函数可表示为
（17）
1.3 微分进化算法
本文建立的优化调度模型属于非线性规划问题，因此采用微分进化算法对其进行求解.
1） 初始化.假设共有N个种群，自变量的个数为D，第n代的种群为Xn.
2） 变异操作.为了使自变量的值产生变化，满足目标函数的要求，需要在自变量中加入变异量
变异量的维数与自变量的个数相等，元素产生方式为
（18）
式中：
为在第n代种群中随机选择的3个自变量；α为控制差分量影响的缩放因子，是介于0～2之间的常数.
3） 交叉操作.交叉操作通过变异量与目标量之间的随机重组，将变异量引入自变量的解集中.交叉过程表示为
（19）
式中：i=1，2，…，N；j=1，2，…，D；φ为0～1之间的随机数；cR为交叉因子，用于指定下一代种群的变化率；r为交叉概率，是一个在0～D中的随机整数.
4） 选择操作.假设待求优化函数为min f（x），则选择操作表达式为
（20）
根据实际运行经验，本文在计算过程中选择种群个数为500，缩放因子为0.6，cR取0.7.
5） 算法改进.微分进化算法在进化过程中，变异与交叉过程是随机的，在寻找最优解的过程中会导致收敛速度较慢.因此本文在保持种群多样性的同时，通过将种群的最优个体引入变异量中，以提高算法的收敛速度，算法改进表达式为
（21）
式中，
为种群中最优个体.
变异量中的缩放因子与交叉因子用于控制算法的搜索速度与范围.寻优过程中，较大的缩放因子有利于完成全局快速搜索，但不利用算法的局部寻优.本文对缩放因子进行动态控制，令其值在0.5～0.75范围内动态变化，控制表达式为
（22）
式中，αn为第n代缩放因子，缩放因子初值α1取0.75.
交叉因子用于控制算法的局部搜索能力，交叉因子越小局部搜索能力越好，在初期可采用较小的交叉因子以提高局部搜索能力；在后期通过增大交叉因子防止算法陷入局部最优.本文对交叉因子进行动态控制，令其值在0.3～0.6内变化，控制表达式为
（23）
式中，
为第n代交叉因子，交叉因子的初值
取0.3.
2 算例分析
文中以IEEE 11节点网络为例，对算法进行验证.图1为电网结构，表1为线路基本参数，其值为标幺值.
图1中，L1～L5为配电网负荷.其中固定负荷所占比例为75%，可转移负荷与可削减负荷所占比例分别为15%和10%.各负荷用户参与转移或削减调度过程中实行阶梯型补偿机制.补偿费用如表2所示.
假设该配电网所有负荷的用户数为20，某一时刻参与负荷削减调度的用户数量服从均值为12，方差为1.25的正态分布，负荷削减量服从均值为10，方差为2.5的正态分布；某一时刻参与转移负荷调度的用户数量服从均值为12，方差为1.4的正态分布，转移负荷量服从均值为6，方差为2.5的正态分布，转移负荷目标时间服从均值为3，方差为1.2的正态分布.
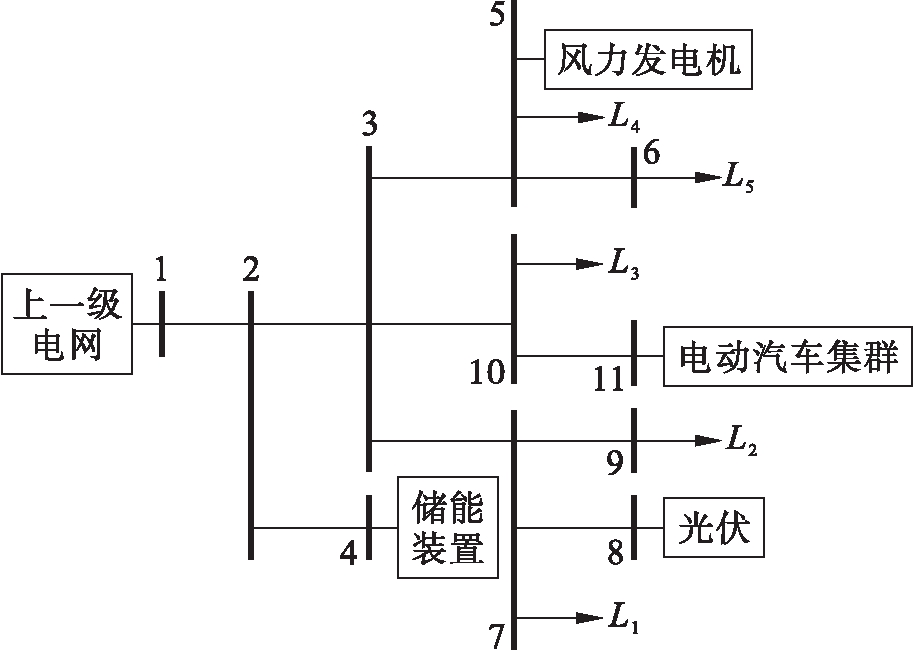
图1 配电网结构
Fig.1 Distribution network structure
表1 配电网线路阻抗参数
Tab.1 Line impedance parameters of distribution network
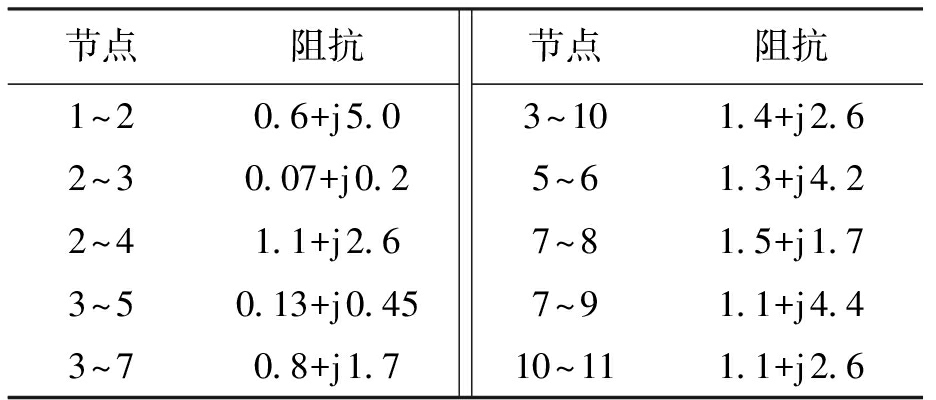
节点阻抗1～20.6+j5.02～30.07+j0.22～41.1+j2.63～50.13+j0.453～70.8+j1.7节点阻抗3～101.4+j2.65～61.3+j4.27～81.5+j1.77～91.1+j4.410～111.1+j2.6
表2 负荷阶梯型补偿费用
Tab.2 Compensation cost of load stages
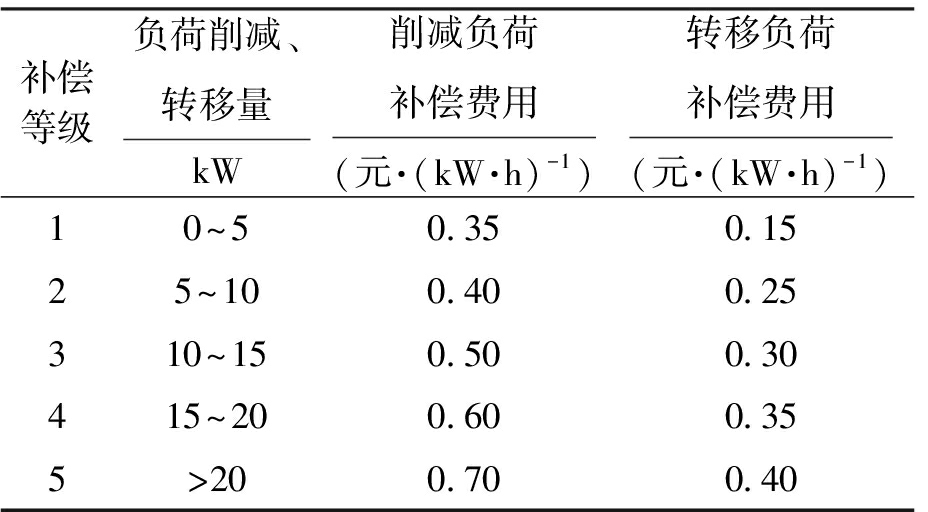
补偿等级负荷削减、 转移量 kW削减负荷补偿费用（元·（kW·h）-1）转移负荷补偿费用（元·（kW·h）-1）10～50.350.1525～100.400.25310～150.500.30415～200.600.355>200.700.40
参与调度的电动汽车为30辆，补偿价格为0.6元/kW·h，每台电动汽车的充电容量为80 kW·h，额定充电功率为10 kW，期望行驶里程500 km.假设电动汽车每天充、放电各一次，开始充电时间服从均值为18，方差为3.5的正态分布；结束充电时间服从均值为8，方差为3.5的正态分布.
电网电价采用三费率分时电价.峰时段（10∶00～15∶00；18∶00～21∶00）电价为0.8元/kW·h；平时段（7∶00～10∶00；15∶00～18∶00；21∶00～23∶00）电价为0.45元/kW·h；低谷时段（23∶00～7∶00）电价为0.25元/kW·h.
利用本文提出的风力、光伏及负荷预测模型得到可再生能源日内典型出力与负荷曲线如图2所示.
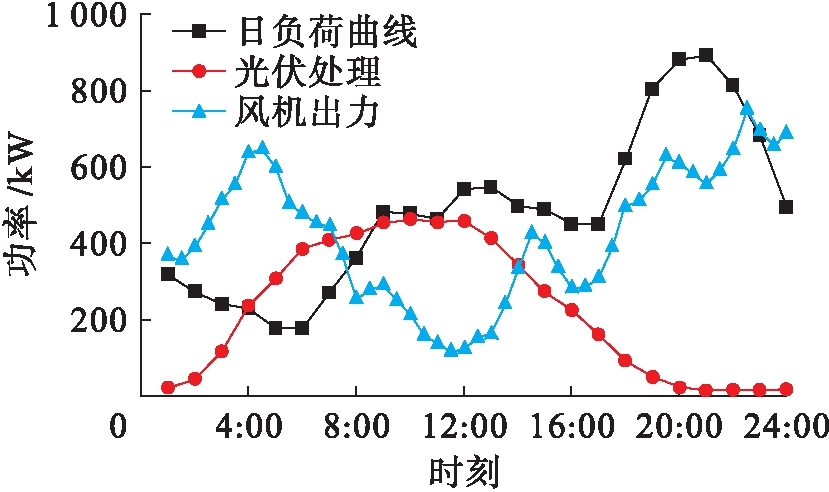
图2 可再生能源出力及负荷预测模型
Fig.2 Prediction model of renewable energy output and loads
为验证调度策略的有效性，本文采用静态优化调度与动态优化调度方法，即常规微分进化算法与改进的微分进化算法对配电网进行优化控制，仿真结果如图3所示.
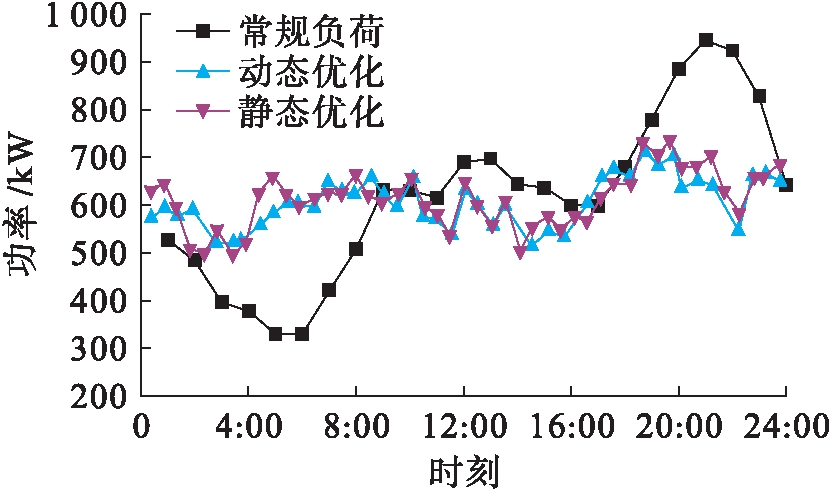
图3 优化控制仿真结果
Fig.3 Simulation results of optimal control
由图3可知，通过对供给侧与需求侧资源的优化调度，负荷曲线相比于优化前有明显的改善.优化前负荷曲线的极差为615.6，标准差为175.5；采用静态优化后的负荷曲线极差为238.6，标准差为59.0；采用动态优化后的负荷曲线极差为195.8，标准差为51.8.由此可见，基于本文所提优化算法得出的负荷曲线具有较为明显的削峰填谷特性，且动态优化的效果优于静态优化.
图4为两种优化算法的结果比较，由图4可知，相比于优化前，静态优化与动态优化模式下分别节约调度成本15.3%、18.9%.优化前为了满足用户的用电需求，不仅需要额外的调度成本，同时存在大量的弃风弃电现象.优化后，可再生能源的利用率由优化前的85%提高到优化后的90%以上，动态优化清洁能源利用率较静态优化提高3.12%.通过对主动配电网的优化控制，减小了弃风弃光成本与购电成本，具有显著的环保效益与经济效益.
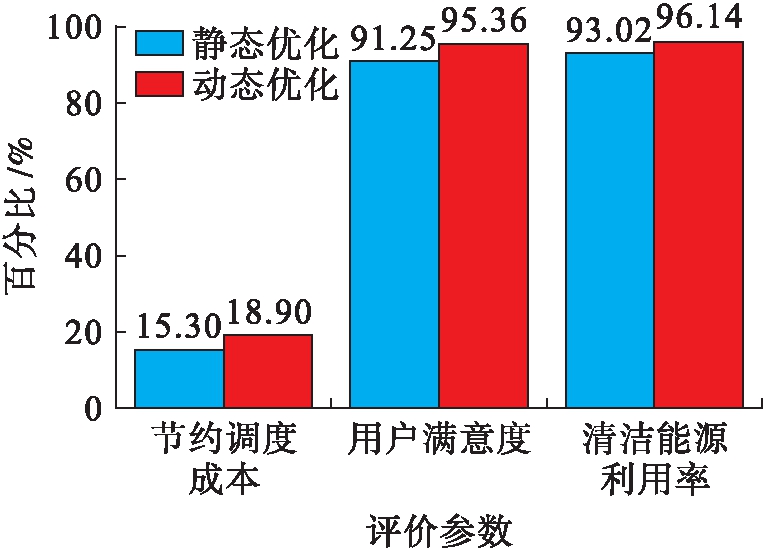
图4 两种模式参数比较
Fig.4 Comparison of parameters between two modes
图5为优化后配网各微电源的输出功率.由图5可知，光伏出力主要集中在6∶00～16∶00区间内，基本为满负荷出力.风力发电机输出功率主要集中在18点后，覆盖了晚间用电的高峰时段，充分实现了清洁能源的有效利用.18∶00～22∶00为一天的用电高峰期，仅依靠风力发电难以满足负荷需求，此时也有部分储能电源开始向电网输出功率.此外，按照本文的调度策略以及负荷的削减与转移原则，23∶00～10∶00为用电低谷与平时段，电动汽车和储能电池陆续充电，既可以节约成本，同时又消纳了多余的风电.
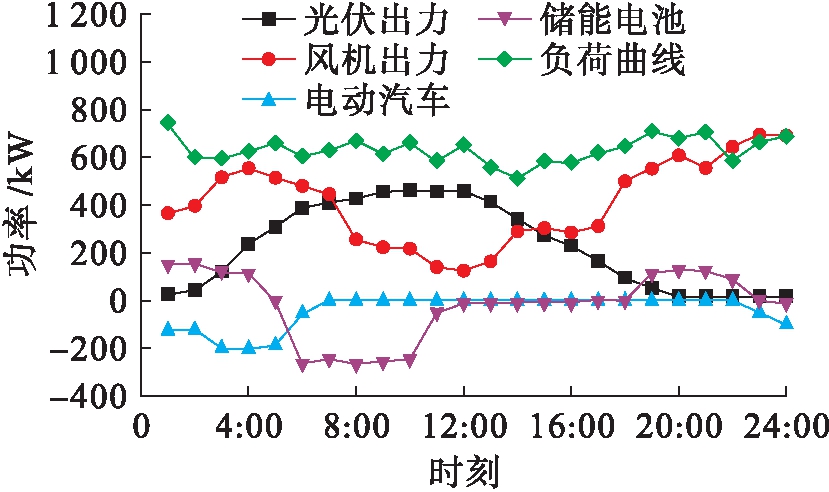
图5 各电源输出功率
Fig.5 Output power of each power supply
综上所述，采用基于微分进化算法的多源协同主动配电网优化控制策略能够在不降低用户满意度的前提下，有效节约调度成本，达到削峰填谷目的，同时有力促进了清洁能源的消纳及综合能源的利用效率.
3 结 论
本文研究了一种基于微分进化算法的多源协同主动配电网优化控制策略.在微分进化算法的基础上，通过引入动态缩放因子与交叉因子，对多源协同的主动配电网进行负荷预测和控制.仿真结果表明，采用动态优化比传统微分进化算法节约成本3.6%，用户满意度提高4.11%，清洁能源利用率提高3.12%.以此为基础，通过协调需求侧与供给侧资源的互动机制，建立了多源协同的主动配电网优化控制模型.优化后配网调度成本可节约15%以上，清洁能源利用率可达90%以上.
[1]葛维春，刘前卫，刘富家，等.高比例清洁能源电网灵活调节方法 [J].沈阳工业大学学报，2018，40（5）：481-485.
（GE Wei-chun，LIU Qian-wei，LIU Fu-jia，et al.Fle-xible adjustment method for power grid with high-proportion clean energy [J].Journal of Shenyang University of Technology，2018，40（5）：481-485.）
[2]潘霄，张明理，刘凯，等.分散式风电并网规划方法 [J].沈阳工业大学学报，2018，40（6）：601-606.
（PAN Xiao，ZHANG Ming-li，LIU Kai，et al.Planning method for dispersed wind power grid-connection [J].Journal of Shenyang University of Technology，2018，40（6）：601-606.）
[3]高强，陈刚，王天群，等.基于线性规划的源网荷储协调控制系统 [J].电子设计工程，2019，27（21）：27-31.
（GAO Qiang，CHEN Gang，WANG Tian-qun，et al.Source network load-storage coordination control system based on linear programming [J].Electronic Design Engineering，2019，27（21）：27-31.）
[4]黄伟，熊伟鹏，华亮亮，等.基于动态调度优先级的主动配电网多目标优化调度 [J].电工技术学报，2018，33（15）：3486-3498.
（HUANG Wei，XIONG Wei-peng，HUA Liang-liang，et al.Multi-objective optimization dispatch of active distribution network based on dynamic schedule priority [J].Transactions of China Electrotechnical Society，2018，33（15）：3486-3498.）
[5]王甜婧，许阔，朱永强.主动配电网的源网荷多层博弈经济调度策略 [J].电力系统保护与控制，2018，46（4）：10-19.
（WANG Tian-jing，XU Kuo，ZHU Yong-qiang.Economic dispatch strategy of active distribution network based on source-network-load multi-layer game [J].Power System Protection and Control，2018，46（4）：10-19.）
[6]孙建军，张世泽，曾梦迪，等.考虑分时电价的主动配电网柔性负荷多目标优化控制 [J].电工技术学报，2018，33（2）：401-412.
（SUN Jian-jun，ZHANG Shi-ze，ZENG Meng-di，et al.Multi-objective optimal control for flexible load in active distribution network considering time-of-use tariff [J].Transactions of China Electrotechnical Society，2018，33（2）：401-412.）
[7]刘东，陈云辉，黄玉辉，等.主动配电网的分层能量管理与协调控制 [J].中国电机工程学报，2014，34（31）：5500-5506.
（LIU Dong，CHEN Yun-hui，HUANG Yu-hui，et al.Hierarchical energy management and coordination control of active distribution network [J].Proceedings of the CSEE，2014，34（31）：5500-5506.）
[8]戴志辉，陈冰研，谢军，等.含多微网的主动配电网分层调度策略 [J].电力系统保护与控制，2018，46（18）：121-127.
（DAI Zhi-hui，CHEN Bing-yan，XIE Jun，et al.Hierarchical scheduling strategy for active distribution network with multi-microgrids [J].Power System Protection and Control，2018，46（18）：121-127.）
[9]谢文强，韩民晓，王皓界，等.基于虚拟电压的直流微电网多源协调控制策略 [J].中国电机工程学报，2018，38（5）：1408-1418.
（XIE Wen-qiang，HAN Min-xiao，WANG Hao-jie，et al.Multi-source coordinated control strategy of DC micro-grid based on virtual voltage [J].Proceedings of the CSEE，2018，38（5）：1408-1418.）
[10]王琛，孟建辉，王毅，等.考虑蓄电池荷电状态的孤岛直流微网多源协调控制策略 [J].高电压技术，2018，44（1）：160-168.
（WANG Chen，MENG Jian-hui，WANG Yi，et al.Multi-source coordinated control strategy considering battery’s SOC for islanded DC microgrid [J].High Voltage Engineering，2018，44（1）：160-168.）
[11]侯文庭，韦化.考虑核电可调度性的风光核水火多源协调短期优化调度 [J].电工技术学报，2018，33（12）：2873-2882.
（HOU Wen-ting，WEI Hua.A multi-source coordinated short-term dispatch model considering the dispatchability of nuclear power plants [J].Transactions of China Electrotechnical Society，2018，33（12）：2873-2882.）
[12]傅晓飞，纪坤华，廖天明，等.含间歇性DG的主动配电网动态重构研究 [J].浙江电力，2018，37（11）：70-78.
（FU Xiao-fei，JI Kun-hua，LIAO Tian-ming，et al.Study on dynamic reconfiguration of active distribution network considering intermittent DG [J].Zhejiang Electric Power，2018，37（11）：70-78.）
[13]张世达，孙永辉，卫志农，等.考虑可控光伏系统概率模型的主动配电网日前优化调度 [J].电网技术，2018，42（1）：247-257.
（ZHANG Shi-da，SUN Yong-hui，WEI Zhi-nong，et al.Day-ahead optimal scheduling for active distribution network considering controllable photovoltaic system via probability model [J].Power System Technology，2018，42（1）：247-257.）
[14]姜兆宇，贾庆山，管晓宏.多时空尺度的风力发电预测方法综述 [J].自动化学报，2019，45（1）：51-71.
（JIANG Zhao-yu，JIA Qing-shan，GUAN Xiao-hong.A review of multi-temporal-and-spatial-scale wind power forecasting method [J].Acta Automatica Sinica，2019，45（1）：51-71.）
[15]于智超，刘帅，杜克文.基于神经网络的风力发电并网控制研究 [J].电子科技，2018，31（8）：89-91.
（YU Zhi-chao，LIU Shuai，DU Ke-wen.Study on control of wind power generation grid connection based on neural network [J].Electronic Science and Technology，2018，31（8）：89-91.）
[16]戴锦，肖文波，胡芳雨，等.光伏发电性能物理预测模型的研究 [J].电源技术，2018，42（2）：262-266.
（DAI Jin，XIAO Wen-bo，HU Fang-yu，et al.Research of photovoltaic prediction model [J].Chinese Journal of Power Sources，2018，42（2）：262-266.）