由于分布式发电机(distributed generators,DG)能够作为持续停电期间的紧急备用电源,同时具有降低配电网电压骤降概率、提高配电网可靠性等功能而被广泛应用.目前,将DG直接连接到配电系统已成为业界的普遍做法,然而,DG的接入给配电网的结构带来了大幅的变化.其在电网中的容量和位置对电网保护系统具有较大的影响,为配电网的控制与保护带来了挑战[1-4].
目前有关分布式发电并网的标准大多是遵循分布式发电不影响电力保护和控制系统正常运行的原则[5-7].当DG连接到配电网中时,短路水平发生变化,因此继电器设置应改变;若DG断开,则继电器设置应恢复到以前的状态.为此,较多通信链路在分布式配电网络中无法使用[8-10].为了降低分布式发电机对电网控制保护系统的影响,本文分析了分布式电源对配电系统的影响因素,并提出了一种确定分布式发电机容量的方法,其能够使电网在插入分布式发电机的同时不会导致电网继电器失去协调性.
1 电网继电保护
图1为一个简单的径向配电系统,其中,GS是电网系统,A、B、C、D、E是系统的节点,其对应的负载分别为负载1~负载5.当电网发生故障时,系统采用反向过流保护.
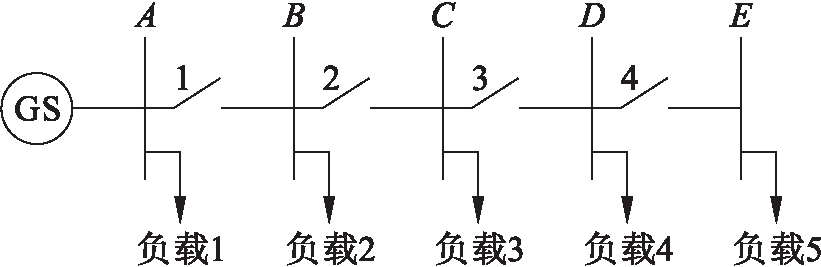
图1 简单的径向配电电源系统
Fig.1 Simple radial distribution power system
继电器1~4的一般运行特性可表示为
(1)
式中:Ki为继电器i(i=1,2,3,4)的时间常数;Idz,i为继电器i的吸合电流;IR,i为继电器i的电流.
当节点D发生故障时,继电器4的动作时间集可以是瞬时的,这是继电器的固有参数.其原理是:当CD部分中出现最大电流,即在节点C发生故障时,继电器3的运行时间至少比继电器4的运行时间长一个特定时间间隔Δt.Δt取决于断路器分闸时间、测量元件的延迟和返回时间等因素.
2 DG互连模式
不同的DG互连模式(即不同数量、位置与容量等)会使继电器的协调性发生变化.图2显示了带有DG的配电网络,由于互连DG的加入,继电器之间的协调关系发生了变化[11-14].
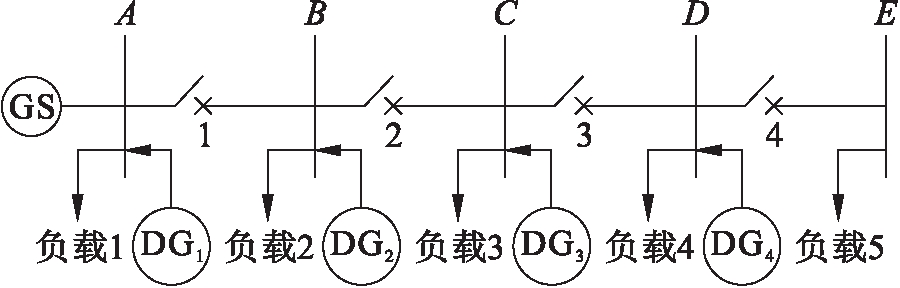
图2 DG配电系统
Fig.2 Distribution system with DG
2.1 单个DG互连
注入DG1后,对于下游故障(例如DE段故障),继电器1、2、3、4将看到下游故障电流,该电流大于没有DG1时的电流,继电器4将消除故障,较大的故障电流将提高系统灵敏度.对于AB、BC或CD段中的给定故障,情况类似.对于上游故障,即在节点A之前发生故障,继电器1~4无法看到上游故障电流,也不会动作.同时,DG1的过流保护装置将检测到故障电流,然后将DG1与公用系统分开,因此,继电器1~4的选择性和协调性将保持不变.
注入DG2后,对于下游故障,继电器1~4将检测到下游故障电流.继电器2~4的故障电流大于无DG时的故障电流,继电器1的故障电流小于无DG时的故障电流.对于AB段的故障,继电器2~4将永远看不到上游故障电流,而继电器1将检测到下游故障电流并运行.在节点A之前发生故障时,继电器1将看到反向故障电流,当故障电流值大于设定值时,继电器1将动作.同时,DG2与下游负荷形成孤岛进而降低平衡率,直至其失衡.该场景与其他位置的DG互连类似.
注入DG1后,对于节点D处的故障,继电器4需要在继电器3之前运行.在这种情况下,如果故障电流大于检测电流,理论上,继电器3和继电器4将同时运行,进而失去协调.事实上,故障电流很少达到检测电流,但由于DG的故障电流贡献,继电器3和继电器4之间的操作时间间隔将缩短.考虑到继电器的固有时间不同,继电器3可能有误动作,为了保持协调,继电器3和继电器4之间的操作时间间隔应保持一个余量ε.如果间隔超过ε,继电器3永远不会在继电器4之前工作.
线性化时间间隔表达式[15]为
t(IR3f)=a1IR3f+b1
(2)
t(IR4f)=c1IR4f+d1
(3)
式中:IR3f为继电器3检测到的故障电流;IR4f为继电器4检测到的故障电流;a1、b1、c1和d1为常数.
进一步可得到余量表达式为
t(IR3f)-t(IR4f)=ε
(4)
将式(2)和式(3)代入式(4),可得故障电流表达式为
(5)
式中,M为常数.
图3描述了节点D处三相故障电流的等效电路.图3中,ZS为系统阻抗;ZDG1为DG1阻抗;Uf|0|为故障点的正常电压;ZAB、ZBC、ZCD分别为AB、BC、CD段的线阻抗,它们等于ZL,If为故障电流.
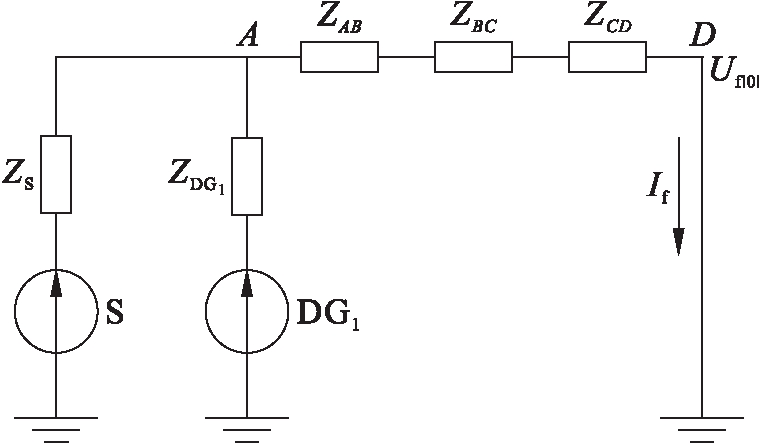
图3 D节点三相故障等效电路
Fig.3 Equivalent circuit for a three-phase fault at node D
如果基本容量为SB,且电源的额定电压等于参考电压UB,则参考电流可写成针对单位计算系统,将故障电流代入式(5)并重新排列,即可得出故障电流为
(6)
从故障位置看到的总阻抗、DG1阻抗和电源阻抗可以相应地表示为
(7)
(8)
ZS*=ZSSB/SS
(9)
根据式(6)~(9)可以导出
因此,节点D处三相故障的DG1最大容量可表示为
对于节点D的相间故障,在节点D发生三相故障的相同条件下,继电器3的故障电流将小于M,继电器3永远不会动作.可以对继电器2进行类似的计算,继电器2永远不会在节点C发生三相故障时运行,继电器1永远不会在节点B发生三相故障时动作,因此,可以确定最大容量SDG1max.注入DG2后,还应限制DG2的容量以确保下游故障的正确操作.
在相同条件下,节点A之前的三相故障电流有![]() 图4为节点A之前三相故障的等效电路.
图4为节点A之前三相故障的等效电路.
由图4可知故障电流为
(10)
式中,![]() 因此,DG2的最小容量可以表示为
因此,DG2的最小容量可以表示为
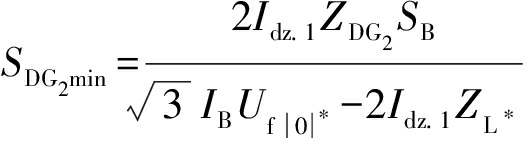
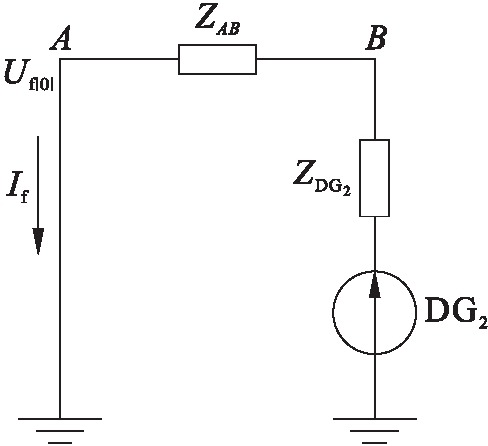
图4 A节点前三相故障等效电路
Fig.4 Equivalent circuit for a three-phase fault before node A
同理可确定DG容量的边界值.
2.2 多个DG互连
DG1和DG2注入,对于DG2的下游故障,继电器1~4的选择性和协调性将保持不变;对于DG1的上游故障,继电器1将运行.然后,DG1将与系统断开,而DG2和下游负载将形成孤岛运行模式.
DG2和DG3注入后,对于DG3的下游故障,继电器1~4的选择性和协调性将保持不变;AB段故障,继电器1动作;对于节点A之前的故障,继电器1、2将获得由DG2和DG3贡献的反向故障电流.在这种情况下,上游电流与DG2和DG3的容量成正比,因此继电器1、2对应的动作时间与DG2和DG3的故障注入能力有关.
在DG1、DG2和DG3注入情况下,对于下游故障,情况类似.继电器2将在BC区发生故障,继电器1将在AB区发生故障.对于节点A之前的故障,继电器1、2的运行时间取决于DG2和DG3的容量大小.显然,如果DG1接在节点D,继电器1~3的动作时间将与DG1、DG2和DG3的容量有关.
DG下游故障情况下,系统选择性和协调性依然存在,灵敏度有所提高;而对于DG上游故障,系统可能会失去协调.
随着DG2和DG3的注入,对于节点D处的三相故障总阻抗可表示为
ZCD*
(11)
根据式(6)和式(11)可得
NZDG3SB-ZDG3SB
(12)
式中,![]()
对于节点A之前的三相故障,继电器1和继电器2将有反向故障电流,分别称为IR1f和IR2f,等效电路如图5所示.
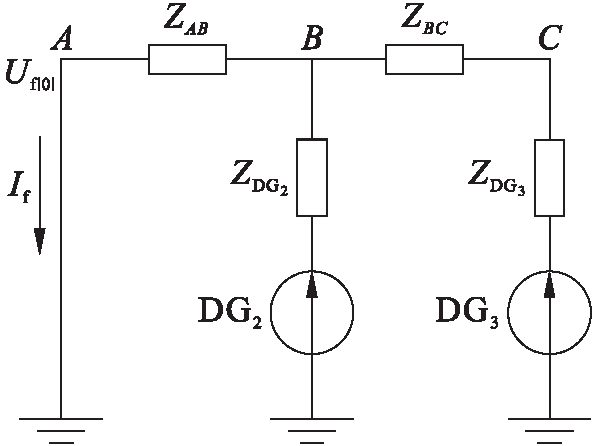
图5 A节点前上游三相故障
Fig.5 An upstream three-phase fault before node A
根据图5可得
(13)
(14)
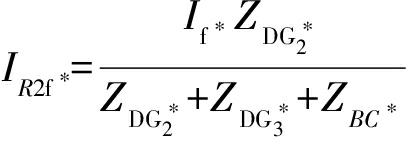
(15)
在这种情况下,继电器1应该在继电器2之前运行.可以通过线性化式(1)减小计算任务,并进一步得到
b2-d2+ε
(16)
式中:A=ZDG2SB;B=ZDG3SB;
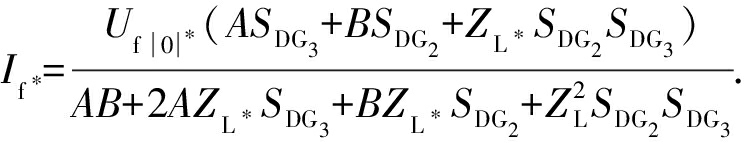
类似地,对于节点A之前的相间故障,可以得到
b2-d2+ε
(17)
式中:ZDG2+、ZDG3+和ZL+分别为DG2、DG3和线路的正序阻抗;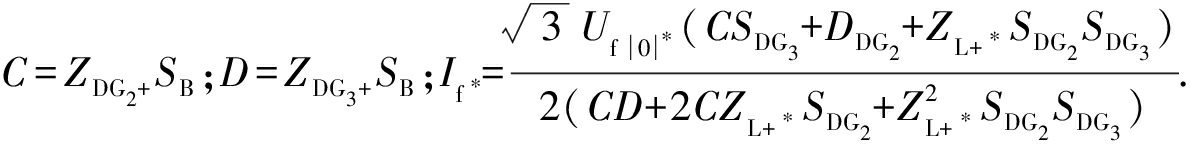
假设正序阻抗等于本文中的负序阻抗.根据式(13)、(16)和(17)可以选择DG2和DG3的容量.
3 仿真实验
考虑具有图1所示的典型拓扑11 kV径向配电系统,所有总线负载均为1 MW,DG的功率因数为0.9.对于每个馈线段,R=0.25 Ω/km.继电器1~4的吸合电流分别为650、500、300及180 A.继电器4被设置为瞬时运行,t4=0.03 s,Δt=0.6 s,K1=0.36,K2=0.26,K3=0.17.
在本文中,3个DG分别位于总线A点、B点与C点,每个DG的容量可以为0.01、0.1、1、2、5、7与10 MW.首先,计算所提及总线的DG最小与最大容量,例如,位于节点B上的DG与继电器4前面的三相故障.记录通过继电器3与4的故障电流,直至继电器3与4之间的动作时间间隔大于或等于余量.
表1显示了继电器4前面的三相故障动作结果,表2显示了继电器3前面的三相故障的动作结果.在表1中,t3与t4是继电器3和4的动作时间,Δt是两个继电器的工作时间之差.当将DG安装在节点D上时,ICD是线路CD上的故障电流.在表2中,t2是继电器2的动作时间.
表1 继电器4前三相故障继电器动作结果
Tab.1 Operation results of relays for three-phase fault in front of relay 4
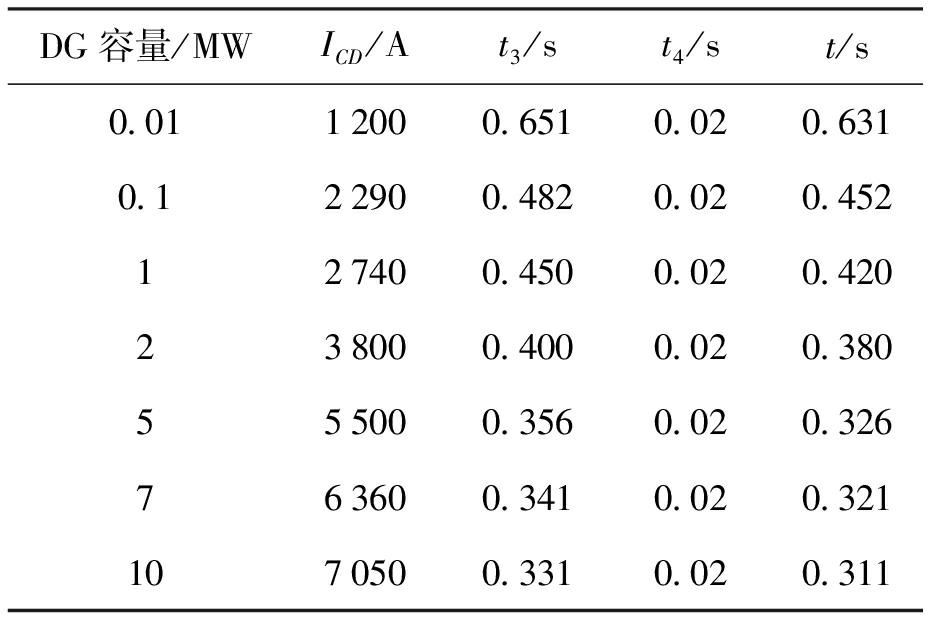
DG容量/MWICD/At3/st4/st/s0.0112000.6510.020.6310.122900.4820.020.452127400.4500.020.420238000.4000.020.380555000.3560.020.326763600.3410.020.3211070500.3310.020.311
表2 继电器3前三相故障继电器动作结果
Tab.2 Operation results of relays for three-phase fault in front of relay 3
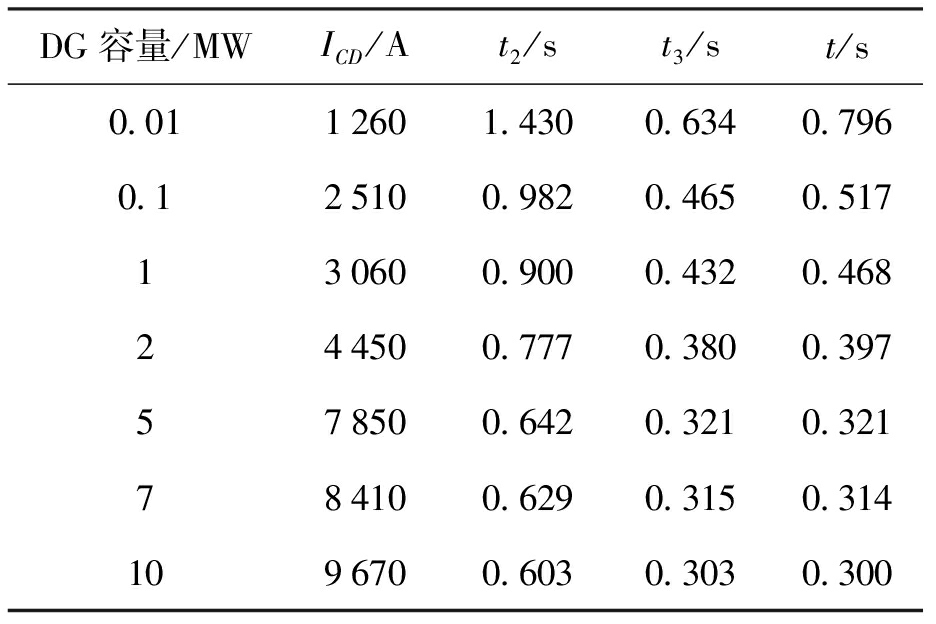
DG容量/MWICD/At2/st3/st/s0.0112601.4300.6340.7960.125100.9820.4650.517130600.9000.4320.468244500.7770.3800.397578500.6420.3210.321784100.6290.3150.3141096700.6030.3030.300
根据表1与表2可以看出,总线的最大容量为10 MW.为了确定总线节点B上DG的最小容量,需考虑节点A的相间故障.表3中显示了不同DG容量下继电器1的操作,其中,操作动作“0”表示操作,“1”表示不操作,IBA是线路BA上的故障电流.由表3可知,总线节点B处的DG最小容量为0.1 MW,对节点A与节点C重复上述过程.表4显示了位于总线节点A、节点B和节点C上的DG最大与最小容量.
表3 A节点单相故障不同DG容量下继电器动作
Tab.3 Relay action of single-phase fault under different DG capacity at node A
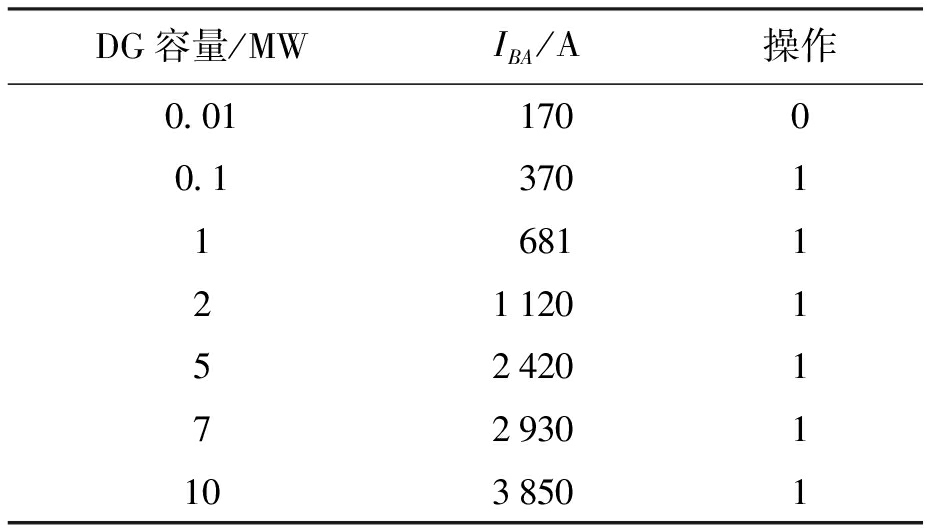
DG容量/MWIBA/A操作0.0117000.13701168112112015242017293011038501
表4 DG容量
Tab.4 DG capacity MW
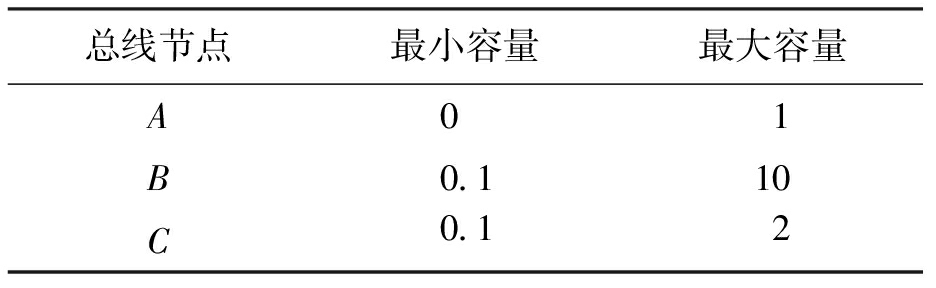
总线节点最小容量最大容量A01B0.110C0.12
将本文计算所得到的DG最大、最小容量与实际容量相比,可知计算值与实际值偏差在5%左右,表明计算结果是可靠的.
4 结 论
配电网络中存在的分布式发电机会导致继电器失去协调性.为了解决该问题,本文提出了一种确定分布式发电机容量的方法,实验和分析结果证明:1)最大和最小容量可以根据单个DG互联的故障电流要求计算;2)对于下游故障,考虑到故障电流不应该引起误动作,可以考虑使用所有容量计算其表达式;3)对于上游故障,考虑相邻继电器的协调,可以考虑使用DG容量计算其表达式.方法可以准确计算出不同模式下保持中继协调时的DG容量.
[1]Nikjoo R,Taylor N,Edin H.Effect of superimposed impulses on AC partial discharge characteristics of oil-impregnated paper [J].IEEE Transactions on Dielectrics and Electrical Insulation,2017,23(6):3602-3611.
[2]Filipe D,Oliveira A D,Xavier G R,et al.Analysis of alternative parameters of dynamic resistance measure-ment in high voltage circuit breakers [J].High Voltage,2019,4(3):197-202.
[3]Bernal E,Spiryagin M,Cole C.Onboard condition monitoring sensors,systems and techniques for freight railway vehicles [J].IEEE Sensors Journal,2019,19(1):4-24.
[4]Aparna N,Vasa N J,Ramanujam S.Optical sensing techniques for condition monitoring of transformer insulation material [J].INAE Letters,2018,2:1-8.
[5]Mitiche I,Morison G,Hughes M,et al.Classification of partial discharge signals by combining adaptive local iterative filtering and entropy features [J].Sensors,2018,18(2):406-420.
[6]Hekmati A,Hekmati R.Optimum acoustic sensor placement for partial discharge allocation in transformers [J].IET Science Measurement & Technology,2017,11(5):581-589.
[7]Peng X S,Wen J Y,Li Z H,et al.Rough set theory applied to pattern recognition of partial discharge in noise affected cable data [J].IEEE Transactions on Dielectrics and Electrical Insulation,2017,24(1):147-156.
[8]Strachan S M,Rudd S,Mcarthur S,et al.Knowledge-based diagnosis of partial discharges in power transformers [J].IEEE Transactions on Dielectrics & Electrical Insulation,2008,15(1):259-268.
[9]Siegel M,Beltle M,Tenbohlen S,et al.Application of UHF sensors for PD measurement at power transfor-mers [J].IEEE Transactions on Dielectrics & Electrical Insulation,2017,24(1):331-339.
[10]Dukanac D.Application of UHF method for partial discharge source location in power transformers [J].IEEE Transactions on Dielectrics and Electrical Insulation,2018,25(6):2266-2278.
[11]Siegel M,Beltle M,Tenbohlen S,et al.Application of UHF sensors for PD measurement at power transfor-mers [J].IEEE Transactions on Dielectrics & Electrical Insulation,2017,24(1):331-339.
[12]Lujano J M,Dufo R,Bernal J L,et al.Probabilistic perspective of the optimal distributed generation integration on a distribution system [J].Electric Power Systems Research,2019,167(2):9-20.
[13]Wei K,Wang D,Chen J Q,et al.Research on distri-buted magnetic circuit calculation of halbach magne-tized permanent magnet generators [J].Applied Mechanics and Materials,2014,70(2):1237-1242.
[14]Lubin M,Dvorkin Y,Backhaus S.A robust approach to chance constrained optimal power flow with renewable generation [J].IEEE Transactions on Power Systems,2016,31(5):3840-3849.
[15]Wilson A,Webster R,Hayes B P,et al.Comparison of two energy storage options for optimum balancing of wind farm power outputs [J].IET Generation,Transmission & Distribution,2016,10(3):832-839.