基站流量精准预测对推进5G无线通信系统的智能化意义重大[1],其中基站流量精准预测一直以来都是一个具有挑战性的问题[2].对5G通信网络流量预测研究采用的大多是一些浅层学习算法,这些算法通常忽略了流量序列蕴含的变化趋势与数据之间的关联性,使得现有流量预测结果通常不能满足实际流量数据原本的特性,造成预测结果与用户需求不符、不准确等一系列问题[3].现有通信网络流量的分析方法主要包括:1)用统计方法对蜂窝网络流量序列进行内在时间模式提取研究;2)对流量序列的空间分布尝试模型拟合的研究;3)通过对时空因素拆分重组进行时空相关性的聚类研究[4-5].
LSTM神经网络算法是一种具有非线性特征以及较强学习能力的神经网络算法[6],该算法具有可通过增加用于控制对过去信息的访问关联,有效解决梯度消失或梯度爆炸现象的优势.压缩感知[7]是一种将信号的采样与压缩过程合二为一,以远低于理想奈奎斯特采样速率进行数据表征并完成数据重构的高效通信技术[8].文中拟基于不同基站的流量时空相关性,首先利用时间序列采集大量通信流量数据,根据低秩特征建立具有块状特性的流量稀疏矩阵;然后再结合时间序列LSTM进行5G通信流量的预测训练,提出基于压缩感知的改进长短时记忆神经网络的基站流量全局建模,精准提升单个基站未来流量值的预测.
1 网络流量预测理论
在信号中,取值较大的数值只占少数,其余多数是取值为0或近似为0的信号,具有该特点的信号称之为可压缩信号[9].在通信信息流中,由于基站提供的通信数据具有时间间隔规律性,使得产生的信号具有较大冗余.因此对提高信号采集效率而言,可采用该流量信号的较大数值用于关联时间信息,即用较小信息量来表征整个流量矩阵.考虑到其满足稀疏特性,所以可用压缩感知的方法对通信数据流做预处理,通过低维度采样匹配原始信息流.
1.1 5G通信网流量信息压缩感知理论
在时间序列预测中,对单个时间序列建模然所采用的方法通常是AR[10]或RNN、LSTM等机器学习方法.虽然这些方法是通过将历史值输入到时间序列以训练获取序列的时间关联性,但当时间序列较多时,该方法工作量较大.为此,引入流量矩阵时间结构特征约束条件建立信息流的高采样压缩感知.
1.1.1 流量时域特性及时间约束条件建立
5G通信网络流量在时间维度上与用户行为具有紧密关联性,在时间上可体现为以日和小时为周期的周期往复性,而当前大部分基站设备并不具备随流量变化的动态跟踪性能.考虑到分层蜂窝网络,假设某小区基站位于多个蜂窝中心,在整个蜂窝网络通信流量稳定的前提下,保证网络基站所有流量均能在工作状态取最大值时满足正常接收,所以得到的约束条件[11]为
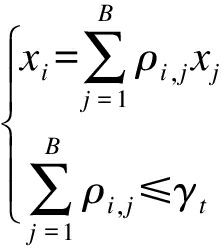
(1)
式中:xi为网络流量;ρi,j为从第i个蜂窝转移到第j个时的用户流量;γt为第t个蜂窝承载的流量峰值的阈值.
5G通信网络下的流量最优化表达式为
(2)
式中:PM和Pm分别为宏蜂和微蜂基站功率消耗;sgn为符号函数,分别用0和1表示网络流量的正常和非正常工作状态;B、BM、Bm分别为满足总数之和的分层、宏、微蜂窝网络中的总基站数,并分别对应各自流量矩阵[12].时间约束条件式(1)反映了小区通信实际流量与预测流量之间的关系,也体现出优化时通信总流量应小于承载总流量的约束要求.
1.1.2 压缩感知约束矩阵建立
传统压缩感知使用的方法主要通过将矩阵按照行或列拆分建立相异向量,再依次叠加构建稀疏向量.但这种方法破坏了信号矩阵行列建立的先验线性约束,且无法满足基站通信网络信息流对时间特征的严重依赖,因此,需要重新提取信息流产生的结构特征,寻找流量矩阵关于时间的依赖条件.设![]() 表示基站流量数据从第i时刻到第j时刻的流量均值,因此,n个基站的通信网络在M个时间间隔中的流量矩阵表示为
表示基站流量数据从第i时刻到第j时刻的流量均值,因此,n个基站的通信网络在M个时间间隔中的流量矩阵表示为
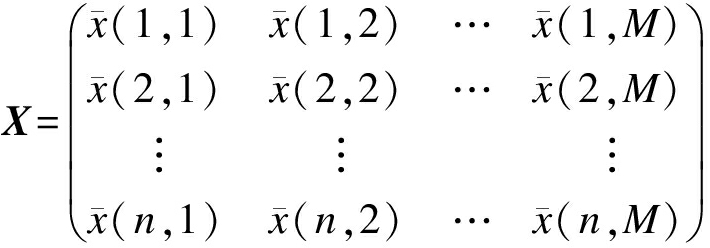
(3)
选定一个阈值,在式(3)所示的矩阵中,将取值低于阈值的划归为0.行向量为基站在不同时间间隔的流量体现;列向量为第j个时间间隔基站的流量均值,行列间约束体现为零值,对应未来预测值.对于低秩矩阵,矩阵求解通常采用近似矩阵尝试奇异值分解的方法,但该方法无法体现矩阵在某个分量上的权重价值,因此文中尝试通过Frobenius范数求低秩矩阵的近似解.
考虑到通信流的时间特性,将上述最优问题式(2)转化为关于时间约束的形式,即
(4)
式中:u为正确观测的权重;![]() 和
和![]() 为原始矩阵近似分解的低秩矩阵特性;α为正则化权重系数;β为倾向于低秩的权重;
为原始矩阵近似分解的低秩矩阵特性;α为正则化权重系数;β为倾向于低秩的权重;![]() 为原始矩阵不同时隙流量约束关系;
为原始矩阵不同时隙流量约束关系;![]() 为网络局部流量观测值约束.
为网络局部流量观测值约束.
1.2 改进算法设计流程
基于压缩感知的LSTM基站流量预测算法的设计流程如图1所示,主要步骤如下:
1) 采集基站流量时间序列,首先进行预处理,然后利用约束条件建立稀疏矩阵.
2) 基于TensorFlow框架,搭建LSTM神经网络.将采集到的大量通信流量时间序列作为该类簇预测模型的训练输入.
3) 评测并选择网络模型权值等参数及暂定模型超参数,并在训练中进行调整.
4) 输入已处理好的基站流量序列数据到LSTM模型,并根据梯度下降算法训练网络.
5) 观察与更改训练模型的迭代次数,计算得到预测输出.如进一步提高精度,可将预测输出值进行反馈及模型调整,从而得到高精度预测输出.
2 基于改进长短时记忆神经网络算法
本文使用Python语言对所提出的基于流量数据压缩感知的LSTM基站流量预测算法进行仿真,并与常规LSTM通信流量算法进行性能对比.
2.1 网络流量预测性能指标
预测精度是算法设计性能优劣的主要指标.为直观体现不同模型下的算法精度,采用预测均值归一化绝对误差进行定量表述,即
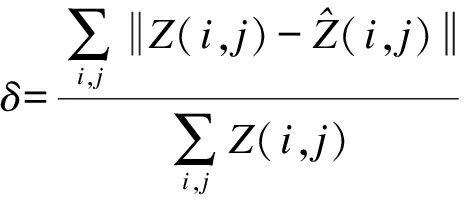
(5)
式中,![]() 分别为观测流量和预测流量数据.
分别为观测流量和预测流量数据.
2.2 实验环境搭建及测试数据生成
TensorFlow是Google公司于2015年11月发布的,目前最为常用且模块可灵活组合的一款深度学习和机器学习框架.本实验通过Tensor-Flow框架[13-16]搭建LSTM神经网络模型生成流量预测模型.实验中使用以下步骤在TensorFlow中生成基站数据的LSTM网络:
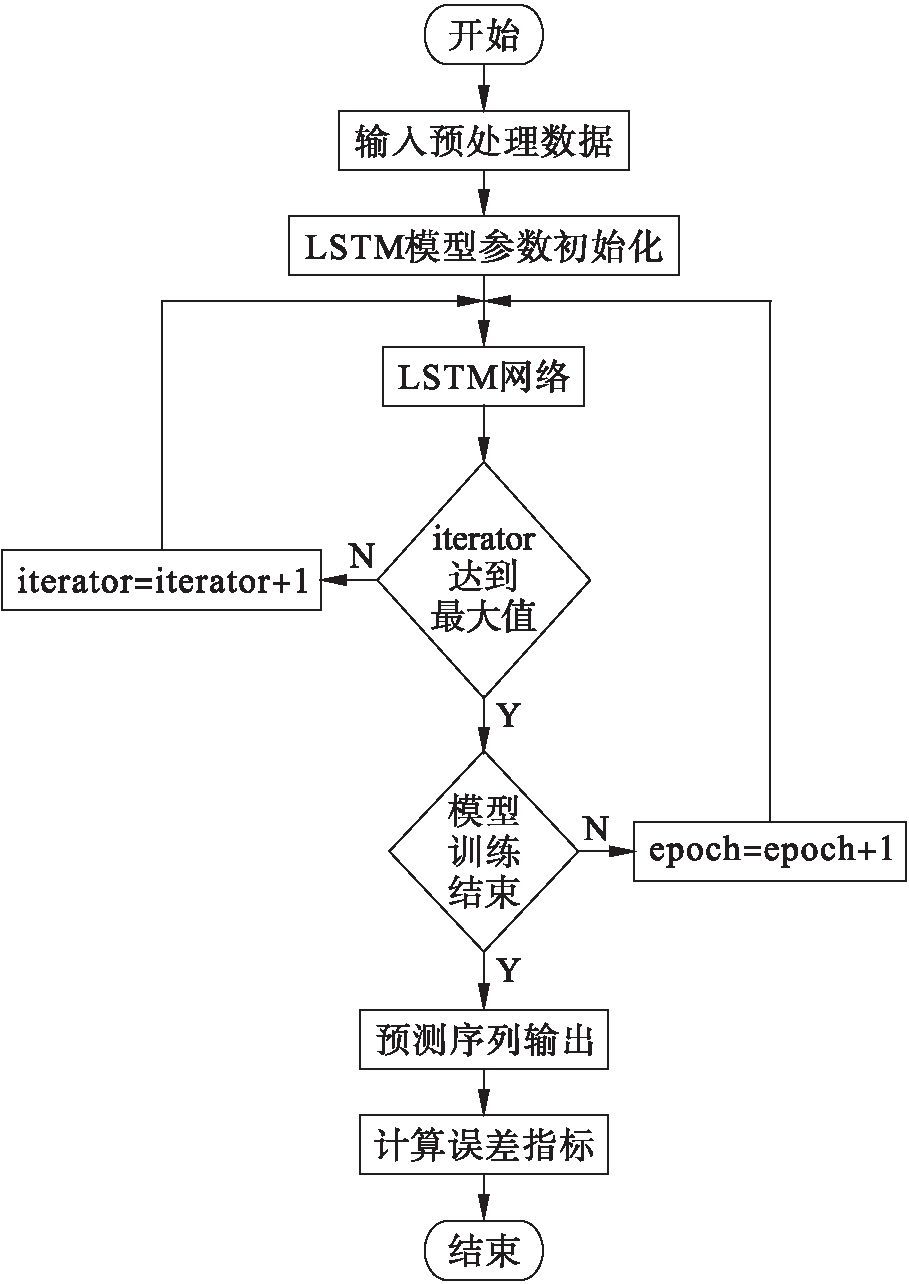
图1 基于压缩感知的LSTM基站流量预测算法的设计流程
Fig.1 Design flow chart of LSTM base station flow prediction algorithm based on compressed sensing
1) 定义x和y的参数和占位符.
batch_size=128
n_x=5#输入单词的数量
n_y=1#输出单词的数量
n_x_vars=1#在其文本中,每个时间步长只有一个变量
n_y_vars=text8.vocab_len
state_size=128
learning_rate=0.001
x_p=tf.placeholder(tf.float32,[None,n_x,n_x_vars],name=’x_p’)
y_p=tf.placeholder(tf.float32,[None,n_y_vars],name=’y_p’)
2) 创建长度为n_x的张量列表.
x_in=tf.unstack(x_p,axis=1,ame=’x_in’)
3) 从输入单元中创建LSTM单元和静态RNN.
cell=tf.nn.rnn_cell.LSTMCell(state_size)
rnn_outputs,final_states=tf.nn.static_rnn (cell,x_in,dtype=tf.float32)
4) 定义最终网络层权重、偏差,最后一层设置为第6个数据选择输出.
5) 创建损失函数和优化器.
loss=tf.reduce_mean(tf.nn.softmin_entropy_logits (logits=x_out,labels=x_p))
optimizer=tf.train.Optimizer (learn_rate=learn_rate).minimize(loss)
6) 创建会话框中运行的精度函数,以检查训练模式的精确性.
7) 考虑到LSTM网络需要在有大量迭代周期的数据集上训练才能够获得更为理想的结果,所以尝试加载完整的数据集重复迭代1 000次训练模型,且每隔100次迭代输出一次结果.
2.3 仿真测试及性能对比分析
2.3.1 仿真测试
本文选取某市中心作为测量地点,随机选取20个基站在近两个月内的流量数据作为文中预测算法的输入对象.按照1.1.2节构造时间间隔为0.5 h的压缩感知特征矩阵,利用距离范式计算相邻基站流量序列的时空相关性,并选取相关性高的前12个基站流量数据值序列作为LSTM的输入数据进行训练.抽取2020年7月至8月共45 d的数据,并将前40 d的基站流量数据作为模型的训练集,训练一个LSTM神经网络预测模型,用以预测后5 d的基站流量.文中将Epoch设为110,隐藏层设为60,最大迭代次数为200次.压缩感知的LSTM流量预测数值与实际流量数值的比较结果如图2所示,其中,横轴时间范围在170 h以前的为训练数据,170~200 h为预测数据;纵轴表示通信网络中流量值的大小.由图2可知,基于时间序列压缩的LSTM流量预测方法更精准地恢复了基于流量的压缩感知数据矩阵,无论是在原始流量数据阶段还是在预测阶段均有较优的体现,且随着时间的增加,预测值与实际测量数据更具有一致性.
2.3.2 算法性能对比
文中首先对每小时通信流量数据做归一化处理,然后基于压缩感知采样平滑数据,提高算法对突变数据的容忍性,从而保持时隙数据变化趋势的一致性.对比测试中,保持2.3.1节中参数取值不变,其他参数选值为:取常数线性关系PM=10Pm,Pm为2 200 W,基站规模Bm、BM、B分别取30、30、60,流量参数ρi,j为2 000 W,γt取2 900 W,对比测试结果如图3所示.常规LSTM方法仅依赖于通信数据流的时间关系,因此造成的归一化误差通常会达到20%.而文中所采用的基于压缩感知的LSTM方法体现了通信数据流在时间与空间方面的序列特性,使得对数据异常点具有更高容忍度及精度.通过归一化的仿真结果表明,其误差估计均值可控制在5%~10%,绝对误差均值在3%~8%.该结果较好地规避了传统基于LSTM通信流量预测方法的不足.与常规LSTM通信流量算法的预测结果相比,平均测量精度可提高近5%.
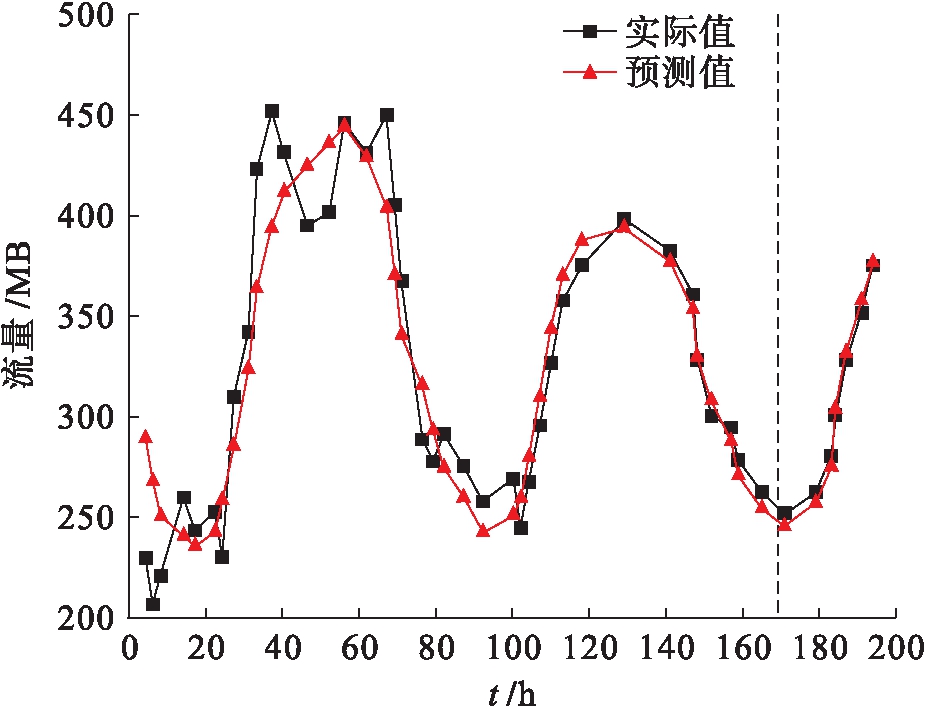
图2 基于压缩感知的LSTM通信网络流量预测数值与实际流量数值的比较
Fig.2 Comparison between predicted and actual flow values for LSTM communication networks based on compressed sensing
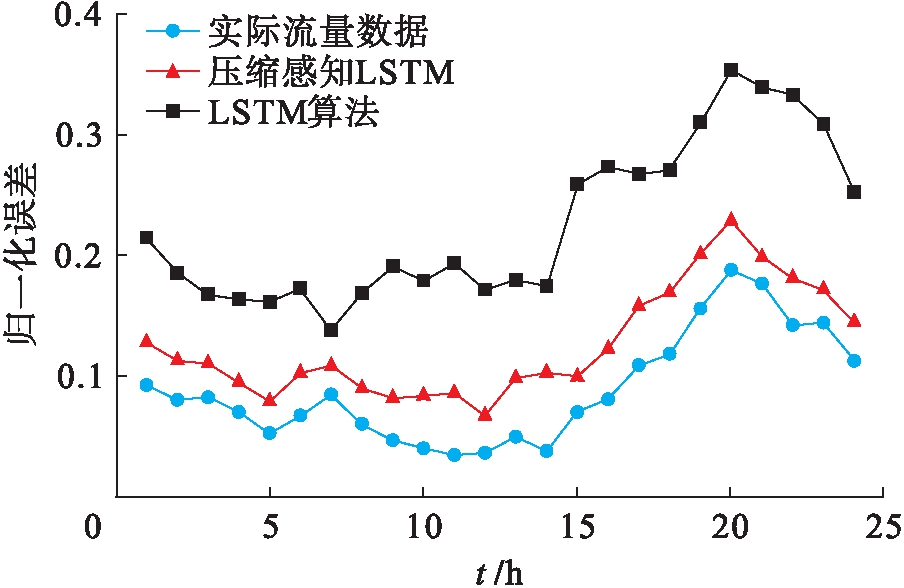
图3 基于压缩感知的LSTM网络流量预测与常规LSTM网络性能对比
Fig.3 Performance comparison for flow prediction between LSTM network based on compressed sensing and conventional LSTM network
3 结 论
本文选取与待预测基站时空相关性较高的基站,并基于压缩感知算法对该基站通信流量数据进行高保真采样,建立具有一致收敛约束条件的稀疏矩阵,最终实现对未来流量数据值的预测.实验仿真表明,本文所提出的改进LSTM算法对通信网络数据流的预测误差均值可控制在5%~10%,绝对误差均值在3%~8%,较常规LSTM通信流量算法预测结果平均精度提高近5%,有效提高了生成模型的准确性.需要注意的是,随着处理器性能的不断提高与改善,若要生成更高精度的预测结果,则可以尝试增加LSTM单元/隐藏层的数量、在较大的数据集上迭代运行模型,这也是未来的研究方向.
[1]宋春雪,文萍,张学晨.基于5G无线通信的稀疏码多址接入系统的FPGA实现 [J].电子技术应用,2016,42(7):8-12.
(SONG Chun-xue,WEN Ping,ZHANG Xue-chen.FPGA implementation of the sparse code multiple access system based on 5G wireless communication [J].Application of Electronic Technique,2016,42(7):8-12.)
[2]段华琼,唐宾徽.基于线性多尺度模型的计算机网络数据流量预测 [J].沈阳工业大学学报,2017,39(3):322-327.
(DUAN Hua-qiong,TANG Bin-hui.Prediction of data flow in computer network based on linear multi-scale model [J].Journal of Shenyang University of Technology,2017,39(3):322-327.)
[3]Roughan M,Zhang Y,Willinger W,et al.Spatio-temporal compressive sensing and Internet traffic matrices (extended version) [J].IEEE/ACM Transactions on Networking,2012,20(3):662-676.
[4]胡铮,袁浩,朱新宁,等.面向5G需求的人群流量预测模型研究 [J].通信学报,2019,40(2):1-10.
(HU Zheng,YUAN Hao,ZHU Xin-ning,et al.Research on crowd flows prediction model for 5G demand [J].Journal on Communications,2019,40(2):1-10.)
[5]徐勇军,彭瑶,余晓磊,等.面向5G协作通信系统的资源分配技术综述 [J].重庆邮电大学学报(自然科学版),2019,31(2):143-157.
(XU Yong-jun,PENG Yao,YU Xiao-lei,et al.Survey on resource allocation techniques for 5G cooperative communication networks [J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition),2019,31(2):143-157.)
[6]李校林,吴腾.基于PF-LSTM网络的高效网络流量预测方法 [J].计算机应用研究,2019,36(12):3833-3836.
(LI Xiao-lin,WU Teng.Efficient network traffic prediction method based on PF-LSTM network [J].Application Research of Computers,2019,36(12):3833-3836.)
[7]Eldar Y C,Kutyniok G.Compressed sensing [M].Cambridge:Cambridge University Press,2009.
[8]Zoha A,Saeed A,Farooq H,et al.Leveraging intelligence from network CDR data for interference aware energy consumption minimization [J].IEEE Transactions on Mobile Computing,2018,17(7):1569-1582.
[9]Malandrino F,Chiasserini C F,Kirkpatrick S.Cellular network traces towards 5G:usage,analysis and generation [J].IEEE Transactions on Mobile Computing,2018,17(3):529-542.
[10]Arvanitakis G,Spyropoulos T,Kaltenberger F.An ana-lytical model for flow-level performance in heterogeneous wireless networks [J].IEEE Transactions on Wireless Communications,2018,17(3):1488-1501.
[11]Bai L,Yao L N,Kanhere S S,et al.Passenger demand forecasting with multi-task convolutional recurrent neural networks [C]//Advances in Knowledge Discovery and Data Mining.Boston,USA,2019:36-51.
[12]Farooq H,Imran A.Spatiotemporal mobility prediction in proactive self-organizing cellular networks [J].IEEE Communications Letters,2017,21(2):370-373.
[13]Thar K,Tran N H,Oo T Z,et al.DeepMEC:mobile edge caching using deep learning [J].IEEE Access,2018,6:78260-78275.
[14]An K,Yan X J,Liang T,et al.Mobility prediction based vehicular edge caching:a deep reinforcement learning based approach [C]//2019 IEEE 19th International Conference on Communication Technology.Xi’an,China,2019:1120-1125.
[15]姜猛,王子牛,高建瓴.基于异构数据联合训练的中文分词法 [J].电子科技,2019,32(4):29-32.
(JIANG Meng,WANG Zi-niu,GAO Jian-ling.Chinese word segmentation based on joint training of hete-rogeneous data [J].Electronic Science and Techno-logy,2019,32(4):29-32.)
[16]许绘香,曹敏,马莹莹.基于大数据分析的非线性网络流量组合预测模型 [J].沈阳工业大学学报,2020,42(6):670-675.
(XU Hui-xiang,CAO Min,MA Ying-ying.Combined prediction model for nonlinear network flow based on big data analysis [J].Journal of Shenyang University of Technology,2020,42(6):670-675.)