深度图像在目标检测、故障检测、轨迹规划、灾害预防、地质勘测、人体姿态估计等众多研究领域中具有重要作用.通过激光雷达、TOF相机以及Kinect等采集深度图像,利用计算机等工具从中获取有用信息,从而为决策指标提供数据支撑[1].但现有的深度图像采集设备受测距原理所限,往往存在分辨率低、有无效像素以及噪声等问题,导致图像边缘不匹配,影响了深度图像的质量,造成区域信息缺失.因此,如何解决深度图像不匹配,增强边缘信息,得到一幅高质量、高分辨率的深度图像成为了计算机视觉领域研究亟待解决的重点问题[2].
国内外相关专家经过多年的研究,从多个角度提出了解决方法.刘金荣等[3]提出了基于联合双边滤波的深度图像边缘增强方法,通过寻找彩色图像与深度图像边缘像素之间的差异,利用联合双边滤波的插值算法进行去噪,引入空洞填充原理进行图像增强.该方法虽然可以避免噪声对边缘的影响,但无法完好地保留细节特征,而且一旦边缘两侧的强度相近,边缘就会变得模糊,造成图像边缘信息失效.孟恬等[4]提出了基于快速行进算法的深度图像边缘增强方法.通过计算各像素与邻域像素之间的多尺度结构相似性,估算深度图像空洞区域像素信息,并进行边缘修复和增强.该方法虽然保留了深度图像边缘的细节特征,但无法填补大面积的图像空洞.李少敏等[5]提出了基于高斯混合模型的Kinect深度图像增强算法.利用高斯混合模型将深度图像分为前景与背景两个部分,分别进行空洞填补与去除噪声处理.该方法虽然速度快,但没有考虑连通区域内部像素与像素之间的差异性,容易造成图像边缘模糊.
针对上述问题,本文提出了基于各向异性扩散算法的深度图像不匹配边缘增强方法,并采用仿真实验,对所提方法的有效性进行了充分验证.
1 深度图像的获取与插值计算
1.1 基于被动测距的深度图像获取
深度图像,又称距离图像,是指将从图像采集器到场景中各点的距离(深度)作为像素值的图像,它直接反映了景物可见表面的几何形状[6].获取深度图像的方法主要分为主动测距和被动测距两种,根据测距方法的不同,获取到深度图像的清晰度不同.
目前研究的深度图像获取方法通常采用主动测距,通过测量工具系统发射光源(电磁波、声波等),然后利用接收反射光获取深度图像,而被动测距通过接收目标物体发射或反射信息,形成深度图像.被动测距技术主要分为单目成像测距与双目立体视觉测距两种,其中双目立体视觉测距技术[7]通过多个摄像机获得同一目标物体的不同角度图像,采用立体匹配算法找到两幅图像中对应的像素点,再依据三角原理计算出各像素点深度值,以获取物体的深度图像.被动测距打破了主动测距中对测量场景的限制,可以在任意场合进行测距,其精度较高,应用范围较小.本文采用被动测距中的双目立体数据测距技术获取深度图像,并对获取后的深度图像不匹配边缘进行增强方法研究.
1.2 深度图像插值计算
由于获取的深度图像与原图像之间存在视觉误差,因此在对深度图像不匹配边缘增强之前,需先对深度图像进行插值计算[8].
深度图像由稀疏像素点组成,这些像素点在排列时,无法避免会出现无效像素,导致图像出现黑色孔洞,而孔洞会在一定程度上使得图像边缘模糊,因此需要计算深度图像孔洞处的像素点灰度值,并进行插值,以此提高深度图像的质量.目前,图像插值算法主要有最近邻插值、双线性插值以及双三次插值三种[9],且后一种均为前一种的优化改进,如表1所示.
表1 图像插值算法
Tab.1 Image interpolation algorithms
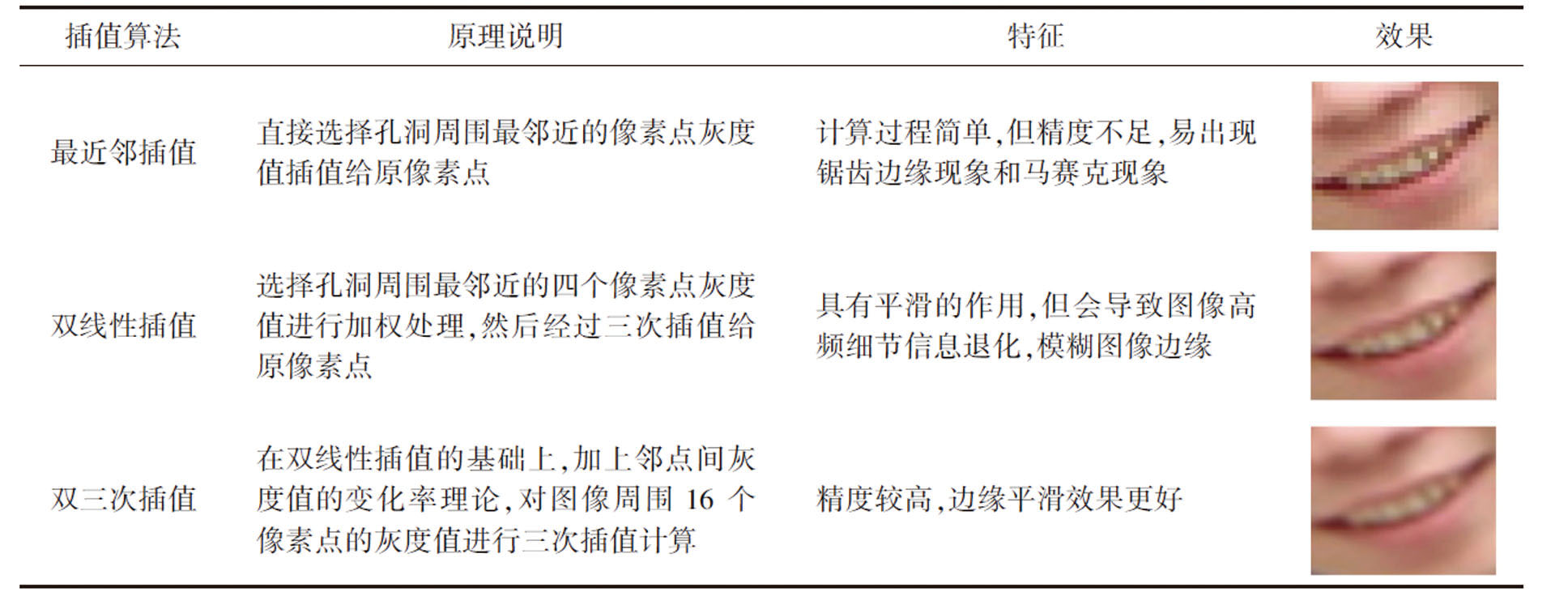
插值算法原理说明特征效果最近邻插值直接选择孔洞周围最邻近的像素点灰度值插值给原像素点计算过程简单,但精度不足,易出现锯齿边缘现象和马赛克现象双线性插值选择孔洞周围最邻近的四个像素点灰度值进行加权处理,然后经过三次插值给原像素点具有平滑的作用,但会导致图像高频细节信息退化,模糊图像边缘双三次插值在双线性插值的基础上,加上邻点间灰度值的变化率理论,对图像周围 16 个像素点的灰度值进行三次插值计算精度较高,边缘平滑效果更好
本文采用双三次插值法对获取后的深度图像进行插值计算,利用邻点间灰度值的变化率求导出深度图像孔洞处的像素点灰度值,实现深度图像质量的增强,以确保后续图像不匹配边缘的增强精度.
1.3 基于加权中值滤波的深度图像滤波
插补后的深度图像边缘像素点的灰度值会存在突变以及不连续的现象,因此还需要对其进行滤波处理,增强深度图像不匹配边缘的对比度.本文采用加权中值滤波法对深度图像进行滤波.
先取得任意一像素点周围所有像素灰度值的中值来代替该点灰度值,从而消除被孤立的噪声点[10].假设h(k,l)为初始图像内任意一像素点的灰度值;∂为h(k,l)的权重系数,Nf(i,j)为f(i,j)的一阶实心,得到中值灰度值的同时保留深度图像中不匹配边缘的细节信息,表达式为
v(i,j)=median{h(k,l)|f(i,j)∈Nf(i,j)}
(1)
该方法排除了深度图像的空洞、噪声等干扰,能够提高后续不匹配边缘增强的准确度和精度.
2 深度图像不匹配边缘增强
2.1 深度图像不匹配边缘检测
不匹配边缘检测是深度图像边缘增强的关键步骤.以往深度图像不匹配边缘检测都是基于局部图像信息实现的,检测效果并不好,因此为寻找深度图像中不匹配边缘轮廓的组成点,在梯度算子基础上[11],采用深度优先遍历[12]的方式进行不匹配边缘检测,具体过程如下:
1) 对待检测不匹配边缘像素点数据结构进行重新构造.
2) 随机选择图像不匹配边缘中任意一点像素点作为出发点.
3) 计算该像素点的灰度值.
4) 在此基础上,估算该像素点周围8个邻域方向上的像素点梯度值.
5) 以此调整该点的灰度值.
6) 判断该像素点是否满足不匹配边缘点特征,若满足,则将该点入栈;否则重新进行计算该像素点周围梯度值,直到满足特征条件为止.
7) 以该像素点为出发点,深度遍历寻找垂直于梯度方向上的边缘点,并标记该点为已访问过的点.遍历过程如下:①判断垂直于梯度方向上的边缘点是否满足图像边缘点特征,若满足,则不断把边缘点入栈,并修改该点相关数据结构;若不满足,则需要原路返回,将该路线中的边缘点出栈处理,直到能从某个小于最大梯度值的方向继续遍历时结束.②当回退到原始出发像素点后,需要按照从上到下、从左到右的顺序搜索判断是否存在没有被访问过的像素点.若存在,则需要重新遍历;若没有,则说明全图遍历结束.
8) 按照遍历顺序,将各像素点连接在一起,形成图像不匹配边缘.
不匹配边缘检测结束后,计算检测到的不匹配边缘像素点到边缘空洞的距离,可得
(2)
式中:S(t)为该像素点位于深度图像不匹配边缘的位置;R(t)为该像素点与不匹配边缘空洞之间的距离;t为像素点.
2.2 基于各向异性扩散算法的不匹配边缘增强
检测到的不匹配边缘中存在空洞,因此,对不匹配边缘空洞进行填补是深度图像不匹配边缘增强方法的中心环节,通过该环节可以使深度图像的不匹配边缘变得平滑,从而达到增强不匹配边缘清晰度的目的.采用各向异性扩散算法进行图像边缘增强[13],其基本原理如下:各向异性扩散算法可通过偏微分方程来表示,即
(3)
式中:f0为初始条件;Δfi为梯度算子;p为散度算子;w(x)为扩散系数,取w(x)=g(Δfi);g(x)为梯度强度;x为各向异性扩散因子.
将式(3)改写为
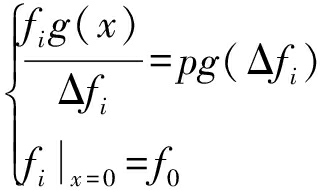
(4)
该方程可以表示为原深度图像在定义域内的媒介,并以非恒定的速度在图像上扩散,而扩散所经过的区域不匹配边缘会变得平滑[14].
当Δfi取0时,满足g(0)=1,g(∞)=0,保证了图像在不匹配边缘区域停止扩散时,不匹配边缘像素点的完整性,此时扩散系数为
(5)
基于上述各向异性扩散算法,构建一种深度图像不匹配边缘增强模型.该模型以完整的深度图像为引导,根据得到的像素点与空洞之间的距离值Y(t),填补空洞像素的缺失,具体过程如下:假定深度图像中某空洞点为m=(i,j),其到深度图像不匹配边缘的最大距离和最小距离分别为C和D;深度图像中目标边缘有效像素点集为Z,以此作为热源,则深度图像不匹配边缘增强可以转换为有效像素点集的热量传导问题[15],用偏微分方程可表示为
![]() =pw(x)Δd(t)
=pw(x)Δd(t)
(6)
式中:λ为时间步长;Δd(t)为单位时间步长的像素点t到空洞点m=(i,j)热量传导深度值;d(t)为深度图像不匹配边缘像素点t到空洞点m=(i,j)的热量传导深度值.
为了增强图像边缘,把各向异性扩散因子x放弃,可得
pw(x)Δd(t)=0
(7)
由此构建深度图像不匹配边缘增强模型,则其增强权重系数为
(8)
式中,U为深度图像不匹配边缘中相邻像素点集.
根据式(7)和(8)得出最终深度图像不匹配边缘增强模型为
(9)
上述方法完成了深度图像不匹配边缘的平滑处理,且得到了不匹配边缘增强模型,根据模型可实现不匹配边缘的增强.整合上述基于各向异性扩散算法的深度图像不匹配边缘增强方法的流程,如图1所示.
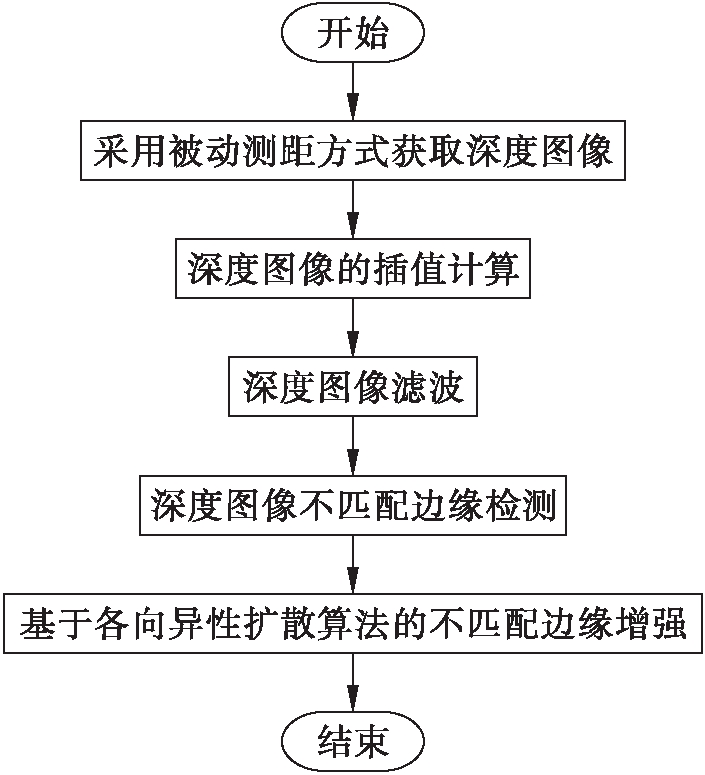
图1 深度图像不匹配边缘增强方法
Fig.1 Mismatched edge enhancement method for depth images
3 仿真实验与结果分析
为验证本文方法的有效性,设计了一组仿真对比实验,将基于联合双边滤波、基于快速行进算法和基于高斯混合模型三种传统深度图像不匹配边缘增强方法作为对比方法,与基于各向异性扩散算法的深度图像不匹配边缘增强方法进行对比测试.
3.1 测试平台
图2为测试平台.具体的实验参数设置为:Δfi=0,g(0)=1,g(∞)=0,步长为2,扩散系数为0.13.利用测试平台中的Xition PRO LIVE和摄像机采集人体姿态原始场景图像和深度图像,其原始场景图像的像素为640×480,如图3所示.

图2 测试平台
Fig.2 Test platform

图3 深度图像获取
Fig.3 Acquisition of depth images
3.2 深度图像不匹配边缘增强效果对比
利用所提方法与三种传统方法对图3b的深度图像不匹配边缘进行增强,得到的增强效果对比结果如图4所示.由图4可以看出,基于高基混合模型的增强方法,增强后图像边缘依然模糊,增强效果最差.基于快速行进算法的增强方法,其增强效果优于前者,基于联合双边滤波的增强方法优于基于快速行进算法的增强方法,而本文所提的增强方法,其图像边缘最为清晰,增强效果最佳.
3.3 深度图像不匹配边缘增强匹配度与清晰度对比
图像边缘增强匹配度与清晰度是测试不同算法性能的重要指标.图像边缘匹配度是增强后深度图像边缘与原始图像边缘之间的契合程度.契合程度越高,增强效果越好,其计算公式为
(10)

图4 不同算法的不匹配边缘增强效果对比
Fig.4 Comparison of mismatched edge enhancement effects among different algorithms
式中:q为契合的边缘像素点数量;qz为总体边缘像素点数量.
图像边缘清晰度可以通过图像边缘的峰值信噪比值来表示,峰值信噪比值越大,图像越清晰,增强效果越好.利用MATLAB分别采用4种不同的方法对图3b的深度图像不匹配边缘进行增强,将增强结果分别与图3a的原始图像进行对比,并对4种不同方法的增强结果进行对比分析,得到4种不同方法的增强匹配度和清晰度对比结果,如表2所示.
表2 不同算法的不匹配边缘增强匹配度与清晰度
Tab.2 Matching degree and clarity of mismatched edge enhancement by different algorithms
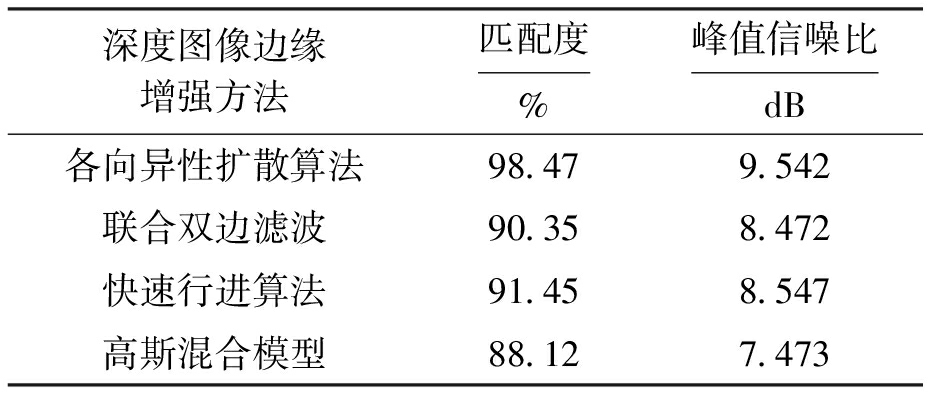
深度图像边缘增强方法匹配度%峰值信噪比dB各向异性扩散算法98.479.542联合双边滤波90.358.472快速行进算法91.458.547高斯混合模型88.127.473
由表2可以看出,利用所提方法对深度图像不匹配边缘进行增强,增强后深度图像边缘匹配度为98.47%,峰值信噪比为9.542 dB.而利用基于联合双边滤波、基于快速行进算法、基于高斯混合模型3种方法对深度图像不匹配边缘进行增强,其增强后深度图像边缘匹配度分别为90.35%、91.45%、88.12%,峰值信噪比分别为8.472、8.547、7.473 dB.上述结果对比可知,所提方法的匹配度最高,峰值信噪比最大,充分说明所提方法的边缘契合程度最高,去噪效果最好,能更有效地增强图像边缘清晰度,使得深度图像中的细节信息更完整.
3.4 深度图像不匹配边缘增强的稳定性
从图像数据库中提取1 200幅图像,测试不同算法处理图像的稳定性,以验证本文算法的实用性能,得到的实验结果如图5所示.
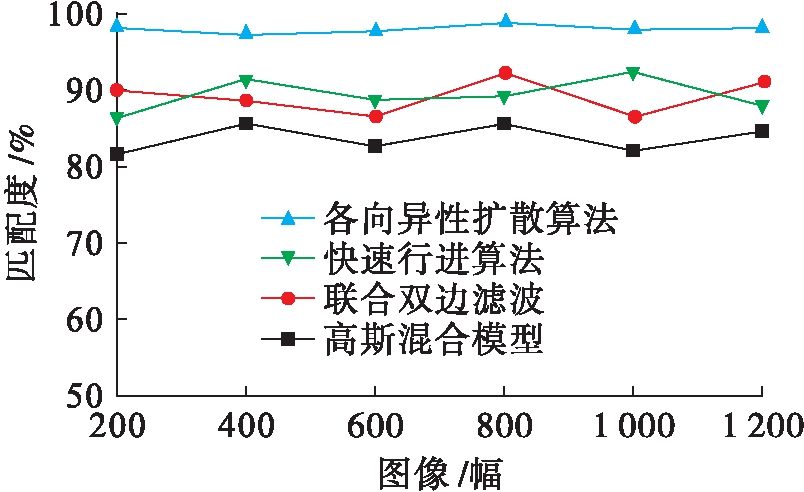
图5 不同算法的不匹配边缘增强的稳定性对比
Fig.5 Stability comparison of mismatched edge enhancement among different algorithms
分析图5可知,依据快速行进算法、联合双边滤波、高斯混合模型处理图像的匹配度均值分别为91.68%、90.51%、88.63%,其处理图像的匹配度变化趋势均较大,稳定性不好,而依据本文所提各向异性扩散算法处理图像的匹配度均值为98.81%,其处理图像的匹配度最高,变化趋势较小,稳定性好.
4 结 论
深度图像是计算机视觉研究中的重点课题之一,深度图像不匹配边缘增强是其中的难点和重点.本文针对三种传统图像边缘增强方法存在的问题,提出一种基于各向异性扩散算法的深度图像不匹配边缘增强方法.该方法利用各向异性扩散实现深度图像不匹配边缘的增强,填补深度图像不匹配边缘的空洞是整个方法的核心步骤.经仿真实验验证,采用该方法时,图像边缘匹配度和峰值信噪比均有了极大改善,由此说明所提方法增强效果更好,提高了图像边缘的清晰度,弥补了边缘信息缺失.
[1]张芳芳,李良福,肖樟树.基于边缘信息引导滤波的深度图像增强算法 [J].计算机应用与软件,2017,34(8):197-200.
(ZHANG Fang-fang,LI Liang-fu,XIAO Zhang-shu.Depth image enhancement algorithm based on edge information guidance filter [J].Computer Applications and Software,2017,34(8):197-200.)
[2]陈洁,周圆,王爱华,等.一种联合重建彩图和深度图的超分辨率重建算法 [J].小型微型计算机系统,2017,38(10):2177-2181.
(CHEN Jie,ZHOU Yuan,WANG Ai-hua,et al.Super-resolution reconstruction algorithm based on joint dictionary learning [J].Journal of Chinese Computer Systems,2017,38(10):2177-2181.)
[3]刘金荣,李淳芃,欧阳建权,等.基于联合双边滤波的深度图像增强算法 [J].计算机工程,2014,40(3):249-252.
(LIU Jin-rong,LI Chun-peng,OUYANG Jian-quan,et al.Depth image enhancement algorithm based on joint bilateral filtering [J].Computer Engineering,2014,40(3):249-252.)
[4]孟恬,全红艳.基于快速行进算法的深度图像增强算法 [J].计算机应用与软件,2017,34(8):225-230.
(MENG Tian,QUAN Hong-yan.Depth image enhancement algorithm based on fast marching method [J].Computer Applications and Software,2017,34(8):225-230.)
[5]李少敏,张倩,王沛,等.基于高斯混合模型的Kinect深度图像增强算法 [J].上海师范大学学报(自然科学版),2016,45(1):28-33.
(LI Shao-min,ZHANG Qian,WANG Pei,et al.Kinect sensor’s depth image enhancement based on Gaussian mixture model [J].Journal of Shanghai Normal University (Natural Sciences),2016,45(1):28-33.)
[6]刘娇丽,李素梅,李永达,等.基于TOF与立体匹配相融合的高分辨率深度获取 [J].信息技术,2016,40(12):190-193.
(LIU Jiao-li,LI Su-mei,LI Yong-da,et al.High-resolution depth maps based on TOF-Stereo fusion [J].Information Technology,2016,40(12):190-193.)
[7]孙深圳,孙洒.关于双目立体视觉图像目标精准匹配仿真 [J].计算机仿真,2018,35(11):413-416.
(SUN Shen-zhen,SUN Sa.Precision matching simulation of binocular stereo vision target [J].Computer Simulation,2018,35(11):413-416.)
[8]尉成勇,邓燕妮.基于改进边缘方向判定方法的图像插值算法 [J].科学技术与工程,2017,17(7):85-89.
(YU Cheng-yong,DENG Yan-ni.Image interpolation algorithm based on an improved judgment method of edge direction [J].Science Technology and Engineering,2017,17(7):85-89.)
[9]丁雪晶.实现图像缩放功能的Matlab插值算法研究与比较 [J].湖北大学学报(自然科学版),2018,40(4):396-400.
(DING Xue-jing.Research and comparison of Matlab interpolation algorithm for image scaling function [J].Journal of Hubei University (Natural Science),2018,40(4):396-400.)
[10]崔光茫,张克奇,徐之海,等.基于仿射重建和噪声散点直方图的图像噪声水平估计 [J].红外与激光工程,2018,47(增刊1):190-196.
(CUI Guang-mang,ZHANG Ke-qi,XU Zhi-hai,et al.Image noise level estimation based on affine reconstruction and noise sample histogram [J].Infrared and Laser Engineering,2018,47(Sup 1):190-196.)
[11]付万程,达飞鹏,黄源.基于分数阶梯度算子的图像匹配算法 [J].图学学报,2017,38(3):352-360.
(FU Wan-cheng,DA Fei-peng,HUANG Yuan.Image matching algorithm based on fractional-order gradient operator [J].Journal of Graphics,2017,38(3):352-360.)
[12]徐成司,董树锋,孙洲,等.基于网络简化和深度优先遍历的配电网路径搜索算法 [J].电力系统自动化,2017,41(24):170-176.
(XU Cheng-si,DONG Shu-feng,SUN Zhou,et al.A path searching algorithm for distribution network based on network simplification and depth first tra-versal [J].Automation of Electric Power Systems,2017,41(24):170-176.)
[13]陈文青,王佰玲,倪国强.基于各向异性扩散的单幅图像去雾算法 [J].光学技术,2017,43(4):354-358.
(CHEN Wen-qing,WANG Bai-ling,NI Guo-qiang.Single image dehazing using anisotropic diffusion [J].Optical Technique,2017,43(4):354-358.)
[14]宋淑红,王双虎.各向异性扩散方程的高精度算法 [J].数值计算与计算机应用,2017,38(4):312-326.
(SONG Shu-hong,WANG Shuang-hu.High accurate computation of diffusion equations with anisotropic coefficients [J].Journal on Numerical Methods and Computer Applications,2017,38(4):312-326.)
[15]周自顾,曹杰,郝群,等.保留边界特征的深度图像增强算法研究 [J].应用光学,2018,39(2):200-206.
(ZHOU Zi-gu,CAO Jie,HAO Qun,et al.Depth image enhancement algorithm for preserving boundary [J].Journal of Applied Optics,2018,39(2):200-206.)