滑移曲线呈现三阶段变化规律；减小钢绞线直径或相对锚固长度，或者增加ECC抗压强度，可以提高平均黏结强度；钢绞线在ECC中的临界保护层厚度为其直径的3.7倍.提出了考虑多因素的高强不锈钢绞线与ECC平均黏结强度及临界锚固长度计算公式，与试验结果吻合良好.摘 要： 为研究高强钢绞线与工程水泥基复合材料的黏结性能，考虑钢绞线直径、相对锚固长度、加固层厚度及ECC抗压强度的影响，对84个棱柱体与12个薄板试件进行单轴拉拔试验.结果表明：拉拔荷载滑移曲线呈现三阶段变化规律；减小钢绞线直径或相对锚固长度，或者增加ECC抗压强度，可以提高平均黏结强度；钢绞线在ECC中的临界保护层厚度为其直径的3.7倍.提出了考虑多因素的高强不锈钢绞线与ECC平均黏结强度及临界锚固长度计算公式，与试验结果吻合良好.
关 键 词： 高强钢绞线； 工程水泥基复合材料； 黏结性能； 拉拔试验； 黏结强度； 锚固长度； 黏结滑移关系； 临界保护层厚度
水泥基复合材料（engineered cementitious composites，ECC）具有优异的应变硬化特性、裂缝控制能力和耐久性等优点[1-4].但ECC自身抗拉强度有限，若采用高强筋材增强ECC可使材料综合性能提升.因此，众多学者相继开展钢筋网、纤维编织网等筋材增强ECC及其加固既有结构受力性能的研究.为使增强筋材与ECC协同工作形成优良的复合材料，许多学者对二者黏结性能进行了研究，包括钢筋、FRP筋、纤维编织网与ECC的黏结性能[5-7]，发现相比于混凝土，ECC与筋材具有更高黏结强度，且黏结破坏表现出更好的延性特征.
由于钢筋强度较低，屈服应变远小于ECC极限拉应变，当用作ECC的增强筋材时，不足以充分发挥ECC应变硬化特性.而FRP筋或编织网的价格相对较高，不利于推广使用于普通结构.高强钢绞线具有高强、耐腐蚀等优点，其极限拉应变（3%～4%之间）和ECC接近，同时较FRP有明显的经济性.因此，本文提出一种新型复合材料——高强钢绞线网增强ECC，并验证了其优越的抗裂、延性和高强度等性能[8].为使二者更好地协同工作，朱俊涛等[9]考虑横向钢绞线影响，研究了高强钢绞线网和ECC黏结性能，但尚未综合考虑ECC强度和保护层厚度等因素的影响.深入了解ECC与高强钢绞线的黏结性能，是对新型复合材料“高强钢绞线网增强ECC”受力性能分析的基础.因此，为推广高强钢绞线网增强ECC的工程应用，亟需进行ECC与高强钢绞线黏结性能的系统研究.本文考虑钢绞线直径、锚固长度、ECC的强度和保护层厚度4个影响因素，对高强钢绞线与ECC黏结性能进行了试验研究.
1.1.1 高强钢绞线在ECC棱柱体中拉拔试件设计
为研究钢绞线的公称直径d、钢绞线锚固长度la、ECC强度（通过改变ECC水胶比r来改变其强度）对高强钢绞线与ECC黏结性能的影响规律，设计5组试件（A*～E*组），每种同样规格试件制作3个，共84个棱柱体拉拔试件.试件详图如图1a所示（单位：mm）.所采用不同水胶比的ECC配合比如表1所示.各试件采用中心置筋，并在ECC试块两端各嵌入内径为8 mm的聚氯乙烯（PVC）管，其长度大于5d，以防止ECC与钢绞线黏结端部因应力集中发生锥形破坏.在5组试件中，B*组中锚固长度为25d的ECC试块以及C*、D*、E*组中锚固长度大于等于15d的ECC试块的尺寸均为100 mm×100 mm×150 mm，其余ECC试块尺寸均为100 mm×100 mm×100 m.
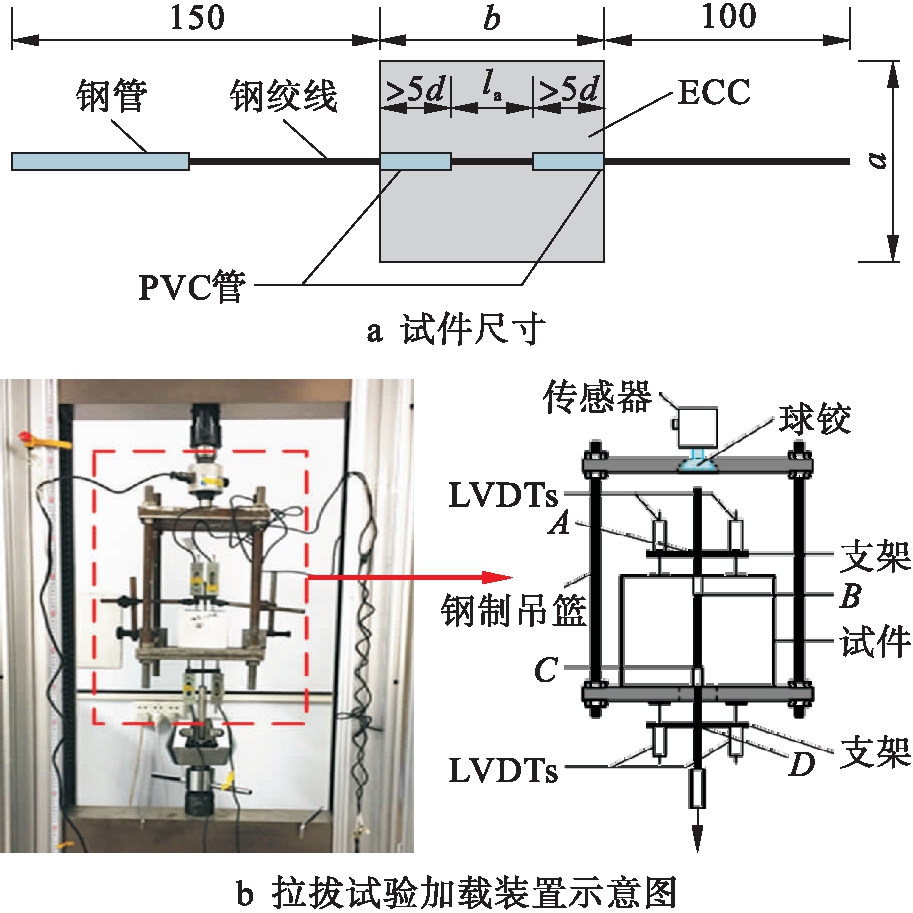
图1 试件尺寸及加载装置示意图
Fig.1 Schematic diagram of specimen size and loading device
表1 ECC配合比
Tab.1 ECC mix proportion
配方水胶比水泥砂粉煤灰微硅粉水减水剂PVA掺量（体积比）/%一0.28010.340.081.150.06752二0.25010.340.081.020.06622三0.23510.340.080.960.06562
1.1.2 高强钢绞线在ECC薄板中拉拔试件设计
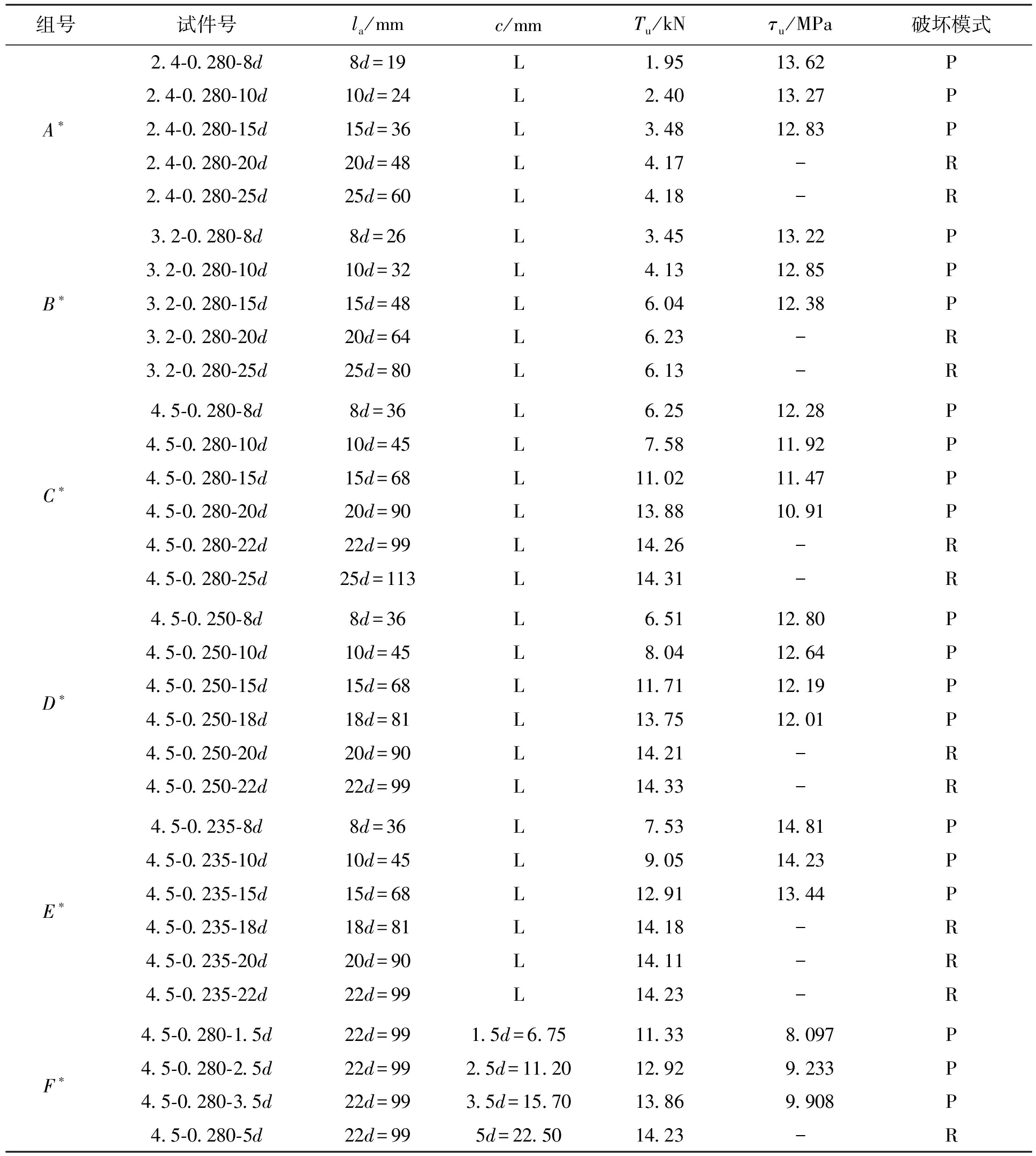
试验以钢绞线的保护层厚度c为试验参数，研究保护层厚度对黏结性能的影响.根据高强钢绞线在ECC棱柱体中拉拔试验结果（见表2），薄板拉拔试件的锚固长度取22d（大于试验确定的有效锚固长度），以防止黏结破坏.薄板试件（定义为F*组）设计为4种工况，每种同样规格的试件制作3个，共12个薄板试件.ECC薄板尺寸为150 mm×150 mm.表2中，试件号第一个数字代表钢绞线直径；第二个数字代表水胶比，第三个数字代表锚固长度；L表示ECC保护层厚度远大于临界保护层厚度；P表示从ECC拉出高强钢绞线；R表示钢绞线断裂；Tu为平均极限拉力；τu为平均结合强度.
表2 拉拔试件设计及试验结果
Tab.2 Design and results of pull-out test
组号试件号la/mmc/mmTu/kNτu/MPa破坏模式A∗B∗C∗D∗E∗F∗2.4-0.280-8d8d=19L1.9513.62P2.4-0.280-10d10d=24L2.4013.27P2.4-0.280-15d15d=36L3.4812.83P2.4-0.280-20d20d=48L4.17-R2.4-0.280-25d25d=60L4.18-R3.2-0.280-8d8d=26L3.4513.22P3.2-0.280-10d10d=32L4.1312.85P3.2-0.280-15d15d=48L6.0412.38P3.2-0.280-20d20d=64L6.23-R3.2-0.280-25d25d=80L6.13-R4.5-0.280-8d8d=36L6.2512.28P4.5-0.280-10d10d=45L7.5811.92P4.5-0.280-15d15d=68L11.0211.47P4.5-0.280-20d20d=90L13.8810.91P4.5-0.280-22d22d=99L14.26-R4.5-0.280-25d25d=113L14.31-R4.5-0.250-8d8d=36L6.5112.80P4.5-0.250-10d10d=45L8.0412.64P4.5-0.250-15d15d=68L11.7112.19P4.5-0.250-18d18d=81L13.7512.01P4.5-0.250-20d20d=90L14.21-R4.5-0.250-22d22d=99L14.33-R4.5-0.235-8d8d=36L7.5314.81P4.5-0.235-10d10d=45L9.0514.23P4.5-0.235-15d15d=68L12.9113.44P4.5-0.235-18d18d=81L14.18-R4.5-0.235-20d20d=90L14.11-R4.5-0.235-22d22d=99L14.23-R4.5-0.280-1.5d22d=991.5d=6.7511.338.097P4.5-0.280-2.5d22d=992.5d=11.2012.929.233P4.5-0.280-3.5d22d=993.5d=15.7013.869.908P4.5-0.280-5d22d=995d=22.5014.23-R
试验加载方案参考Canadian Standards Association（CSA）标准[10]，关于拉拔试验方法的规定，采用100 kN电伺服万能试验机对试件进行拉拔试验，试验加载装置及位移计（LVDT）布置如图1b所示.试验采用位移控制，速度为0.3 mm/min.直至发生如下现象时停止加载：1）钢绞线被拔出或者断裂；2）ECC试件破坏.试验过程中，由于钢绞线最大拉拔力仅为14 kN左右，因此可忽略ECC试块的变形.自由端伸出的AB段钢绞线在加载过程中没有变形，故把自由端的位移计所测得的数据SA即认为是自由端B点处钢绞线与ECC的相对滑移.下端位移计测量的是钢绞线的D点相对试件锚固段最底部C点的滑移，但CD段钢绞线的变形较大，不能忽略.试验中CD段钢绞线的变形为
SCD=PlCD/EsAs
（1）
式中：P为施加拉力；Es为钢绞线弹性模量；As为钢绞线截面面积；lCD为CD段钢绞线长度.加载端钢绞线相对ECC的实际滑移SL为
SL=SD-SCD
（2）
式中，SD为下端位移计测得的位移.平均滑移量计算公式为
S=（SL+SA）/2
（3）
式中，SA为自由端滑移量.锚固长度内的平均黏结应力τ计算公式为
τ=F/（πdla）
（4）
式中，F为平均极限拉拔力.
制作ECC采用的原料有普通硅酸盐水泥、粉煤灰、微硅粉、细沙、PVA纤维、水及高效减水剂.试验按照3种不同的水胶比r各浇筑5个试件，标准养护28 d（抗压试件为边长70.7 mm的立方体，受拉试件为13 mm×40 mm×280 mm薄板），并进行ECC的单轴受压和受拉试验，确定ECC抗压强度fcu、受拉开裂强度ftc、抗拉强度fet以及极限拉应变εu，试验结果如表3所示.对3种直径钢绞线试样各取3个进行受拉试验，测得的平均拉断力Pu、极限抗拉强度fy、平均弹性模量Es、极限拉应变εu如表3所示.
表3 ECC和高强钢绞线材料性能
Tab.3 Material properties of ECC and high-strength steel wire strands
ECCrfcu/MPaftc/MPafet/MPaεu/%高强钢绞线d/mmPu/kNfy/MPaEs/GPaεu/%0.28028.751.8092.6092.702.44.221502.75126.12.620.25032.762.2372.7600.673.26.261329.56123.72.390.23540.092.9273.2160.824.514.211476.82108.13.61
2.1.1 ECC棱柱体拉拔试验破坏模式
当锚固长度较小时，试件发生拔出破坏，其荷载达到峰值后突然下降，且滑移量迅速增加，荷载下降到一定程度后不再降低，而是出现小幅上下波动，滑移量仍继续增加，直到钢绞线拔出.拨出破坏模式如图2所示，可见ECC基体粉末嵌入钢绞线表面钢丝之间，说明钢绞线拔出过程中，其表面钢丝间的基体被挤碎切断.随着锚固长度增大，平均极限拉拔力也增加，当拉拔力增至钢绞线拉断力后试件发生钢绞线断裂破坏.所有试件ECC试块表面均未出现裂缝.各试件试验结果如表2所示.
图2 ECC棱柱体试件拔出破坏图
Fig.2 Failure mode of ECC prismatic specimens with pull-out failure
2.1.2 ECC棱柱体拉拔试验荷载滑移曲线及破坏机理
图3为部分典型试件的拉拔荷载平均滑移曲线.图3a中试件4.5-0.280-25d的荷载平均滑移曲线只有上升段，这是由于其锚固长度较大，界面黏结力大于钢绞线拉断力而导致拉断破坏.分析图3中具有拔出破坏模式试件的荷载平均滑移曲线，分为上升段、下降段、残余段.已有研究表明，筋材（钢筋、FRP筋、高强钢绞线）与ECC的黏结力主要由化学胶结力、摩擦力和机械咬合力组成，并在不同受力阶段这三种力的贡献不同，结合本文拉拔试验现象分析，可以揭示高强钢绞线与ECC黏结力在各受力阶段的变化规律如下：
上升段（OA段）.即从零点（O点）到峰值荷载A点；加荷初期，曲线呈线性上升，这是由于界面黏结力主要由化学胶结力提供，相对滑移较小；当荷载增至极限荷载的10%～20%时，曲线开始非线性上升，这是由于随着滑移量增大，化学胶结力从加载端向自由端逐渐丧失，界面力转由界面机械咬合力和摩擦力提供，使得滑移量增速加快，直至峰值荷载.
下降段（AB段）.即从峰值点A到荷载开始停止下降点B之间的阶段；达到峰值后曲线开始非线性快速下降，这是由于钢绞线表面钢丝间的基体被挤碎切断，咬合齿破坏导致荷载迅速下降，滑移量快速增大；且界面基体颗粒不断被磨细，导致摩擦力也不断下降.
残余段（BC段）.滑移量增至一定值后，基体颗粒被充分磨细后摩擦力不再下降，使荷载保持基本不变（残余承载力约为峰值荷载的50%～60%），但由于界面不均匀性发生小幅波动.
2.1.3 黏结性能影响因素分析
在图3a中，对于钢绞线拔出破坏试件，随着锚固长度增大，峰值拉拔荷载不断增大，峰值荷载对应的滑移量也不断增大，且在上升段内相同荷载对应的滑移量减小.这是由于增加锚固长度，可以提供更大的黏结面积，从而增加界面总黏结力和整体刚度.由图3b可知，随着钢绞线直径增大，试件峰值拉拔力增大，且在上升段内相同荷载对应的滑移量减小.这是由于随着钢绞线直径增大，黏结面积增加，从而提供更大界面整体黏结力和刚度.由图3c可知，随着ECC抗压（抗拉）强度提高，峰值荷载增大，但其对应滑移量几乎不变，且在上升段内相同荷载对应的滑移量减小.这是由于ECC强度越高（即水胶比越低），其与钢绞线的化学胶结力越大，且基体越不易被挤碎或切断，从而增加界面整体黏结力和刚度.
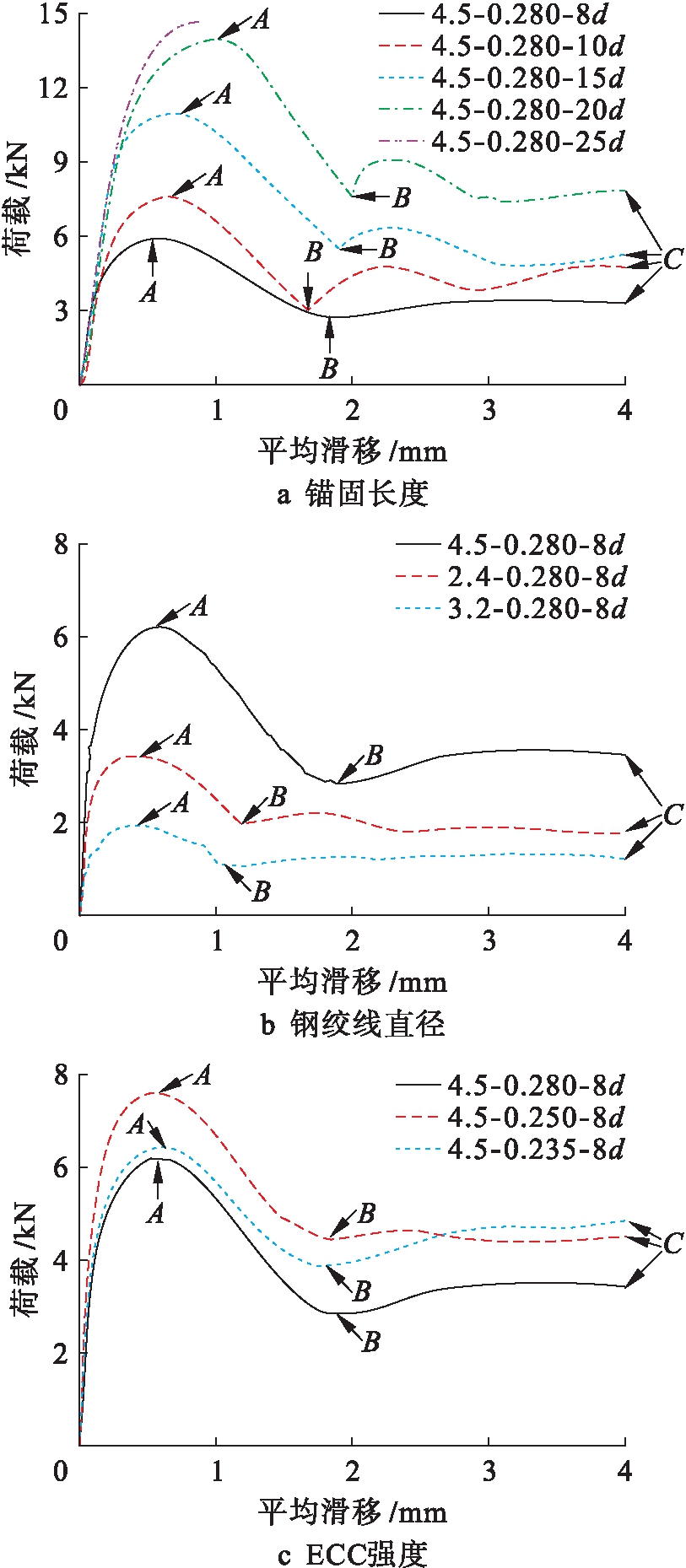
图3 参数对ECC棱柱体拉拔试件荷载滑移关系的影响
Fig.3 Influences of parameters on load-slip relationships of ECC prismatic pull-out specimens
2.2.1 ECC薄板拉拔试验现象分析
对于保护层厚度为1.5d、2.5d、3.5d的ECC薄板试件，加载至开裂荷载（分别为其峰值荷载的10%、15%、30%）时，试件加载端底部中间出现竖向细小裂缝；荷载增至峰值荷载的20%～30%时，试件上端开始出现滑移.随着荷载继续增加，裂缝向上延伸，且下部裂缝宽度也在增加.当达到峰值荷载时，伴随“砰”的响声，保护层厚度为1.5d、2.5d的试件竖向裂缝贯通，滑移迅速增大，荷载快速下降；当荷载降至一定值后不再单调降低，此时裂缝最大宽度达到约0.2 mm；之后荷载波动式下降至一定值（即残余承载力，分别约为其峰值荷载的30%、40%）后便维持在该值小幅波动，且裂缝宽度也不再增大，直至钢绞线拔出，如图4a、b所示.对于保护层厚度为3.5d的试件达到峰值荷载时，伴随“砰”的响声，其竖向裂缝延伸至约试件3/4高度处，并未贯通，之后荷载迅速下降，而滑移量快速增加；当荷载降至一定值后不再单调下降，此时最大裂缝宽度达到0.08 mm，之后荷载波动式下降至残余承载力，并小幅波动（残余承载力约为其峰值荷载的45%），且裂缝宽度也不再增大，直至钢绞线拔出，如图4c所示.保护层厚度为5d的试件均发生了钢绞线拉断破坏，且试验过程中ECC薄板都未出现裂缝，如图4d所示.
图4 薄板拉拔试件破坏图
Fig.4 Failure modes of thin plate pull-out specimens
综上所述，随着ECC保护层厚度增加，提供更大的横向约束力，试件由劈裂拔出破坏转变为钢绞线断裂破坏.当厚度增至3.5d时，荷载已增至约14 kN，接近钢绞线拉断力，裂缝并未贯通，说明此时的保护层厚度已接近临界保护层厚度.另外，由于ECC中短纤维的桥联作用，出现劈裂裂缝的试件是裂而不碎，仍保持良好的完整性，且裂缝宽度较小.
2.2.2 ECC薄板拉拔试验荷载滑移曲线及破坏机理
图5为不同保护层厚度试件的典型荷载平均滑移曲线.由图5可见，试件4.5-0.280-5d的荷载滑移曲线只有上升段，且峰值荷载与试件4.5-0.280-3.5d接近，说明保护层厚度大于3.5d后，黏结强度已变化不大.劈裂拔出破坏的ECC薄板试件的荷载滑移曲线可分为上升段、单调下降段、波动下降段、残余段4个阶段.上升段（OA段）：加载初期，曲线呈线性上升，该阶段界面力主要由化学胶结力承担；当达到峰值荷载的10%～20%时，曲线进入非线性变化，这是由于化学胶结力逐渐丧失，界面力主要由机械咬合力和摩擦力承担，但由于保护层厚度不足，导致ECC基体出现劈裂裂缝，且随荷载增加而不断扩展，从而使得滑移量随荷载的增速变大，直至达到峰值荷载.单调下降段（AB段）：当荷载达到峰值后，迅速降低，而滑移量快速增加，这是由于ECC的劈裂裂缝贯通（或者迅速扩展），导致钢绞线表面和ECC的贴合度降低，使得界面机械咬合力和摩擦力迅速下降，而滑移量突增.波动下降段（BC段）：当曲线下降到B点后，出现上下波动，但整体仍是下降趋势，这是由于随着钢绞线逐渐被拔出，界面ECC基体颗粒不断被磨细，导致摩擦力下降；同时由于界面的不均匀性而发生小幅波动.残余段（CD段）：滑移量增加到一定值后，基体颗粒被充分磨细，摩擦力不再下降，使残余荷载基本保持在一定数值.
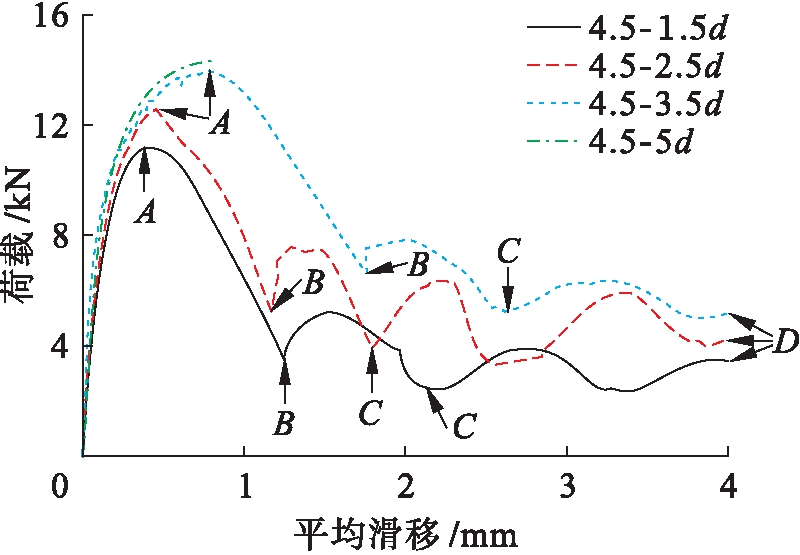
图5 不同保护层厚度ECC薄板拉拔试件荷载滑移曲线对比
Fig.5 Comparison of load-slip curves for ECC thin-plate pull-out specimens with different cover thickness
由图5可见，对于出现劈裂裂缝的试件，随着保护层厚度的增大，试件峰值拉拔荷载及对应滑移量越大，进入残余阶段时的残余承载力也越大.这是由于增加ECC保护层厚度，可提高ECC抗劈裂能力并约束劈裂裂缝的发展，从而提高抗拔承载力.另外，试件4.5-3.5d的荷载滑移曲线上升段与试件4.5-5d的曲线很接近，再次说明3.5d已接近临界保护层厚度.
图6为黏结强度与影响因素关系曲线.图6a为不同锚固长度试件的平均黏结强度τu与钢绞线直径的关系曲线.由图6a可见，在其他条件相同情况下，随着直径增加，钢绞线与ECC的最大平均黏结应力（即平均黏结强度）基本呈线性减小.分析其原因，由于泊松效应，钢绞线纵向拉伸时会导致径向收缩，从而降低钢绞线与ECC的贴合度，减弱两者间的机械咬合力和摩擦力，导致黏结强度降低.
图6b为不同钢绞线直径试件的平均黏结强度τu与相对锚固长度la/d的关系曲线，可以看出，在其他条件相同情况下，随着锚固长度的增加，峰值拉拔荷载增大，但高强钢绞线与ECC的平均黏结强度却逐渐降低，且基本呈线性减小.分析其原因，由于试件中存在应力拱而引起的黏结应力峰值效应现象，使得界面应力分布并不均匀，且锚固长度越长，应力分布越不均匀，高应力区占黏结总长度的比例较短，故平均黏结强度较低.
图6c为不同锚固长度试件的平均黏结强度τu与ECC抗压强度fcu平方根的关系曲线，可以看出，在其他条件相同的情况下，随着ECC强度等级的提高，高强钢绞线与ECC的平均黏结强度增大，且平均黏结强度与ECC抗压强度平方根基本呈线性关系.根据前文分析，界面化学胶结力、机械咬合力、摩擦力均随着ECC抗压强度增加而提高，从而使平均黏结强度得到了提高.
图6d为发生劈裂拔出破坏的薄板拉拔试件的相对平均黏结强度τu/τ0与相对保护层厚度c/d的关系曲线.τ0=10.15 MPa，为当薄板试件的拉拔力等于高强钢绞线平均拉断力时对应的平均黏结应力.由图6d可见，在其他条件相同的情况下，随着相对保护层厚度的增加，高强钢绞线与ECC的相对平均黏结强度呈线性增大.利用最小二乘法进行线性回归分析得到τu/τ0与c/d的关系式为
τu/τ0=0.091 3c/d+0.662
（5）
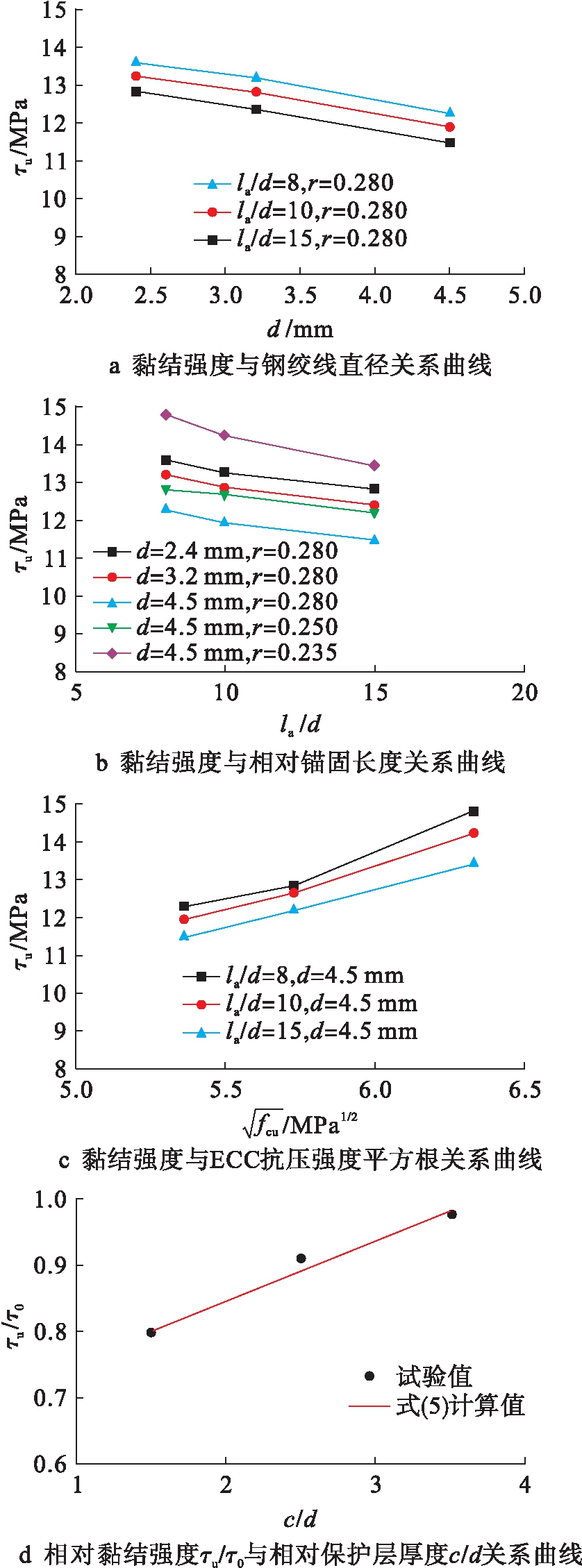
图6 黏结强度与影响因素关系
Fig.6 Relationship between bond strength and influencing factors
式（5）的相关系数为0.989.根据试验结果，当c/d>3.5时，增加保护层厚度对钢绞线与ECC的黏结强度影响较小.令式（5）等于1，可得到ECC相对临界保护层厚度为c/d=3.7，即当保护层厚度大于3.7d时，黏结强度不再增加，即不再出现劈裂裂缝.则式（5）的适用条件为：c≥3.7d时取c=3.7d.
根据上述分析，基于前文中对试验结果分析得到的高强钢绞线直径、锚固长度、保护层厚度以及ECC强度对黏结强度的影响规律，并参考文献[11]假定各因素的影响相互独立，对拉拔破坏试件（除试件4.5-0.280-20d和4.5-0.250-18d外）的平均黏结强度的试验结果进行了统计回归拟合，得到高强钢绞线与ECC平均黏结强度以及各影响因素的关系式为
（1.228-0.136d/d2.4）·
（2.458-0.018la/d）
（6）
式中：当c/d>3.7时，取c/d=3.7；d2.4为公称直径为2.4 mm的钢绞线.该拟合公式与试验结果的相关系数为0.996.
未参与拟合的试件4.5-0.280-20d和4.5-0.250-18d的平均黏结强度试验值τu，c分别为10.94 MPa、11.88 MPa，按照式（6）计算得到的平均黏结强度计算值τu，t分别为10.91 MPa、12.01 MPa.可以看出，式（6）能较准确地预测高强钢绞线与ECC的平均黏结强度.
为得到ECC保护层厚度大于临界保护层厚度的情况下高强钢绞线与ECC的临界锚固长度，令平均黏结强度乘以钢绞线与ECC的接触面积等于钢绞线的拉断力，即式（7），可以得到不同直径钢铰线在不同水胶比的ECC中的临界锚固长度lc的值，其表达式为
（2.458-0.018lc/d）πdlc=Pu
（7）
表4为临界锚固长度计算与试验结果对比.将表4中按式（7）计算的临界锚固长度值lc，7与各影响因素（包括ECC抗压强度fcu、钢绞线直径d和抗拉强度fy）的关系进行拟合分析，得到临界锚固长度简化计算公式为
（8）
将式（8）计算得到的临界锚固长度lc，8列于表4，可以看出，按式（8）与式（7）计算结果的比值lc，8/lc，7的平均值为1.0，变异系数为0.039.说明式（8）能较准确计算临界锚固长度.
表4 临界锚固长度计算与试验结果对比
Tab.4 Comparison between calculated and test results for critical anchorage lengths
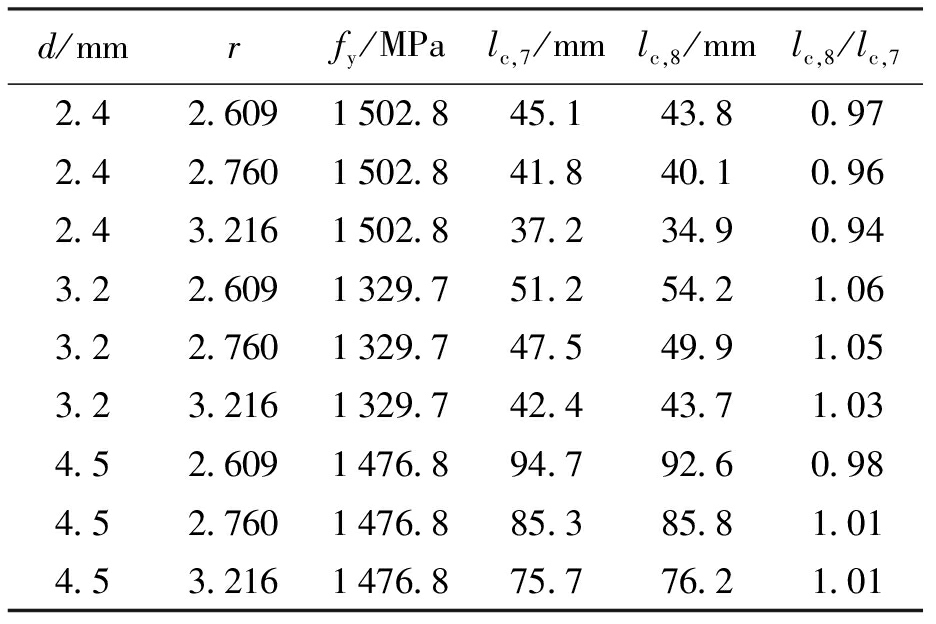
d/mmrfy/MPalc,7/mmlc,8/mmlc,8/lc,72.42.6091502.845.143.80.972.42.7601502.841.840.10.962.43.2161502.837.234.90.943.22.6091329.751.254.21.063.22.7601329.747.549.91.053.23.2161329.742.443.71.034.52.6091476.894.792.60.984.52.7601476.885.385.81.014.53.2161476.875.776.21.01
本文通过分析得出以下结论：
1） 当保护层厚度大于临界保护层厚度时，ECC不会出现劈裂裂缝，发生拔出破坏试件的荷载滑移曲线可分为上升段、下降段与残余段；当小于临界保护层厚度时，ECC出现劈裂裂缝，但裂而不碎，荷载滑移曲线可分为上升段、单调下降段、波动下降段与残余段.
2） 随着高强钢绞线直径或锚固长度增加，钢绞线在ECC中的峰值拉拔力及对应滑移值均增大，但平均黏结强度线性减小.随着ECC抗压（抗拉）强度增大，峰值拉拔力增大，但其对应滑移值基本不变，且平均黏结强度与ECC抗压强度的平方根线性正相关.
3） 高强钢绞线在ECC中的临界保护层厚度为钢绞线直径的3.7倍.在不大于临界保护层厚度值时，平均黏结强度随相对保护层厚度增加呈线性增加趋势，当其值大于临界保护层厚度值时，继续增大保护层厚度，平均黏结强度保持不变.
4） 考虑锚固长度、保护层厚度、ECC基体抗拉强度、高强钢绞线直径4个影响因素，提出高强钢绞线与ECC间的平均黏结强度及临界锚固长度计算公式，与试验结果吻合良好.但该公式是在有限试验数据基础上得到的，还需要进一步研究来验证其有效性.
[1]江世永，龚宏伟，姚未来，等.ECC材料力学性能与本构关系研究进展 [J].材料导报，2018，32（23）：4192-4204.
（JIANG Shi-yong，GONG Hong-wei，YAO Wei-lai，et al.A survey on mechanical behavior and constitutive model of engineered cementitious composite [J].Materials Review，2018，32（23）：4192-4204.）
[2]刘泽军，李艳，温丛格.PVA-ECC劈裂抗拉强度与变形性能试验研究 [J].建筑材料学报，2016，19（4）：746-751.
（LIU Ze-jun，LI Yan，WEN Cong-ge.Experimental study on strength and deformation performance of PVA-ECC under splitting tension [J].Journal of Building Materials，2016，19（4）：746-751.）
[3]杨建波，文辉，唐继辉，等.超高韧性水泥基复合材料研究综述 [J].青海交通科技，2020，32（2）：97-100.
（YANG Jian-bo，WEN Hui，TANG Ji-hui，et al.Review of research on ultra-high toughness cement-based composites [J].Qinghai Transportation Science and Technology，2020，32（2）：97-100.）
[4]鲍文博，王怀成，王东旭.PVA纤维及尾矿砂掺量对GTCC自愈合性能影响 [J].沈阳工业大学学报，2020，42（2）：226-230.
（BAO Wen-bo，WANG Huai-cheng，WANG Dong-xu.Effect of PVA fiber and tailing sand content on self-healing properties of GTCC [J].Journal of Shenyang University of Technology，2020，42（2）：226-230.）
[5]Deng M K，Pan J J，Sun H Z.Bond behavior of deformed bar embedded in engineered cementitious composites under cyclic loading [J].Construction and Building Materials，2019，197：164-174.
[6]Deng M K，Pan J J，Sun H Z.Bond behavior of steel bar embedded in engineered cementitious composites under pullout load [J].Construction and Building Materials，2018，168：705-714.
[7]Wang H L，Sun X Y，Peng G Y，et al.Experimental study on bond behaviour between BFRP bar and engineered cementitious composite [J].Construction and Building Materials，2015，95：448-456.
[8]王新玲，杨广华，钱文文，等.高强不锈钢绞线网增强工程水泥基复合材料受拉应力应变关系 [J].复合材料学报，2020，37（12）：3220-3228.
（WANG Xin-ling，YANG Guang-hua，QIAN Wen-wen，et al.Tensile stress-strain relationship of engineered cementitious composites reinforced by high-strength stainless steel wire mesh [J].Acta Materiae Compositae Sinica，2020，37（12）：3220-3228.）
[9]朱俊涛，李燚，王新玲.考虑横向钢绞线影响的钢绞线网/工程水泥基复合材料黏结性能试验研究 [J].工业建筑，2018，48（11）：143-148.
（ZHU Jun-tao，LI Yi，WANG Xin-ling.Experimental research on bonding performance of stainless steel wire mesh/ECC with horizontal steel wire [J].Industrial Construction，2018，48（11）：143-148.）
[10]Canadian Standards Association.CAN/CSA S806-12 Design and construction of building components with fibre-reinforced polymers [S].Ottawa：Canadian Standards Association，2012.
[11]林红威，赵羽习.变形钢筋与混凝土黏结性能研究综述 [J].建筑结构学报，2019，40（1）：11-27.
（LIN Hong-wei，ZHAO Yu-xi.Bond behavior between concrete and deformed steel bar：a review [J].Journal of Building Structures，2019，40（1）：11-27.）