由于钢管混凝土[1-4]自身的特点决定了其在土木工程中的巨大应用前景,各国学者利用内填混凝土的变化,分别对钢管普通混凝土、钢管再生混凝土、微膨胀钢管混凝土、钢管高强混凝土、钢管轻集料混凝土、钢管自密实混凝土、钢管赤泥混凝土等进行了深入的研究.同时,由于钢管与内填混凝土的粘结作用决定了钢管混凝土的工作性能,因此,1975年Virdi等[5]率先开展了钢管混凝土的粘结强度研究,之后又有大量的学者进行了各种类型内填混凝土的粘结滑移研究工作.其中,池建军[6]完成了34根钢管混凝土试件的推出试验,探讨了钢管混凝土界面抗剪粘结力并对影响因素进行了分析,得到了抗剪粘结强度计算公式;丁庆军等[7]进行了30根钢纤维微膨胀钢管混凝土试件推出试验,系统研究了核心混凝土与管壁的界面粘结性能,阐述了界面的粘结破坏特征;陈宗平等[8]进行了31根钢管再生混凝土试件的推出试验,分析了变化参数的影响,探讨了粘结强度的计算方法,推导了粘结剪力传递长度的计算公式;傅中秋等[9]通过对27根钢管轻集料混凝土试件的推出试验,研究了钢管轻集料混凝土粘结滑移的发展过程及破坏机理,对钢管轻集料混凝土粘结强度的影响因素进行了分析;申鑫[10]对22根方钢管混凝土试件进行了试验研究,在试验的基础上进行了非线性有限元分析,为方钢管混凝土短柱轴压承载力设计理论提供了参考;黄晖等[11]进行了14根圆钢管自密实混凝土的反复推出试验,分析了自密实钢管混凝土的界面粘结状况以及膨胀剂掺量对试件粘结滑移性能的影响;武斌等[12]制作了15个圆钢管赤泥混凝土短柱试件进行推出试验,得出了圆钢管赤泥混凝土的荷载滑移曲线,并对变化参数的影响进行了分析.
上述研究虽然得到了相应的粘结强度计算公式,但都是适用于各自类型内填混凝土的计算公式,尚未有一个统一的粘结强度简化计算方法.因此,本文通过收集国内外钢管混凝土的粘结滑移试验数据,对影响粘结强度的影响因素进行分析,并在此基础上拟合出钢管混凝土粘结强度统一计算方法,以此来补充钢管混凝土的粘结滑移理论.
1 粘结强度影响因素分析
1.1 混凝土强度的影响
由于混凝土浇筑的试验条件、钢管内壁的情况等不利因素的影响,从各国学者的研究来看,混凝土强度对粘结强度的影响程度尚不完全确定,但从本文查找的文献资料统计发现,大多数情况下,在径(宽)厚比、长径(宽)比、套箍系数不变的前提下,粘结强度随着钢管内填混凝土强度的提高而提高,如图1所示.由图1可见,虽然内填混凝土种类不同,但是粘结强度均随混凝土强度的提高而提高,只是提高程度有所不同.这主要是因为混凝土强度越高,其化学胶结力也相应提高,而化学胶结力正是钢管与混凝土界面粘结强度的重要组成部分.
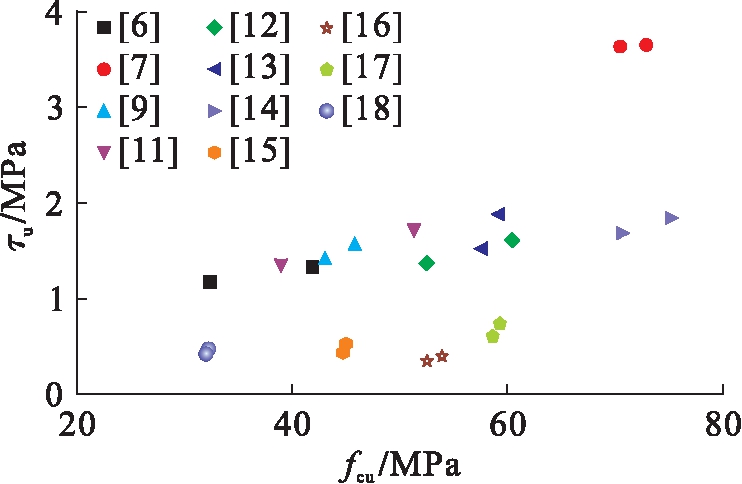
图1 混凝土强度与粘结强度的关系
Fig.1 Relationships of concrete strength coefficient and bond strength
1.2 长径(宽)比的影响
图2为钢管混凝土长径(宽)比与极限粘结强度的关系.由图2可见,在混凝土强度、径(宽)厚比、套箍系数相同的情况下,极限粘结强度与长径比呈正比例关系,即随试件长径(宽)比的提高而提高.这主要是因为随着长径(宽)比的提高,试件更容易产生偏心受压变形,由于产生了一定的弯曲变形,导致内填混凝土与钢管壁挤压程度提高,从而提高了界面的抗滑移能力.
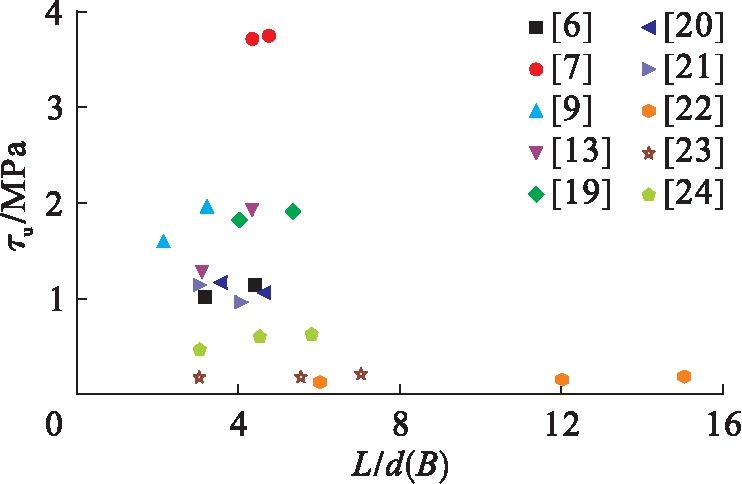
图2 长径(宽)比与粘结强度的关系
Fig.2 Relationships of L/d(B) and bond strength
1.3 径(宽)厚比的影响
图3为钢管混凝土径(宽)厚比与极限粘结强度的关系.由图3可见,在混凝土强度、长径(宽)比、套箍系数相同的情况下,试件的极限粘结强度与径(宽)厚比呈反比例关系,即试件极限粘结强度随径(宽)厚比的减小而增加,这主要是因为一方面随着径(宽)厚比的减小,套箍系数相应增大,提高了钢管对内填混凝土的约束,从而提高了界面的抗滑移能力;另一方面径(宽)厚比越小,内填混凝土体积越小,由于水化热的影响,内填混凝土的收缩小于径(宽)厚比大的试件,从而增加了混凝土与钢管壁的接触,提高了界面的挤压作用,也就提高了界面的抗滑移能力.
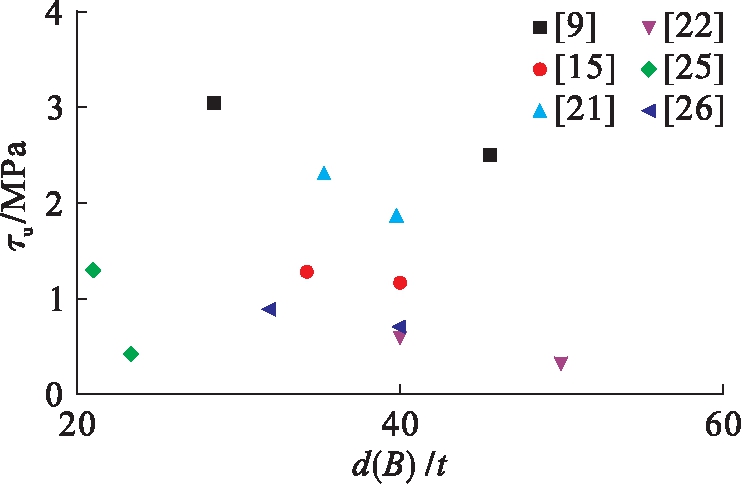
图3 径(宽)厚比与粘结强度的关系
Fig.3 Relationships of d(B)/t and bond strength
1.4 套箍系数的影响
由于钢管混凝土是通过钢管壁对内填混凝土进行约束,并提高其力学性能,因此套箍系数是钢管混凝土中重要的指标.图4为钢管混凝土套箍系数与极限粘结强度的关系.由图4可见,在混凝土强度、长径(宽)比、径(宽)厚比相同的情况下,试件的极限粘结强度与套箍系数呈正比例关系,即试件极限粘结强度随套箍系数的增加而增加,这主要是因为随着套箍系数的增大,钢管壁对内填混凝土的约束增强,提高了钢管壁与内填混凝土接触面上的挤压力,从而提高了界面的摩擦力,也就提高了极限粘结强度.同时通过套箍系数能够有效地回避混凝土强度对极限粘结强度影响的不确定因素.
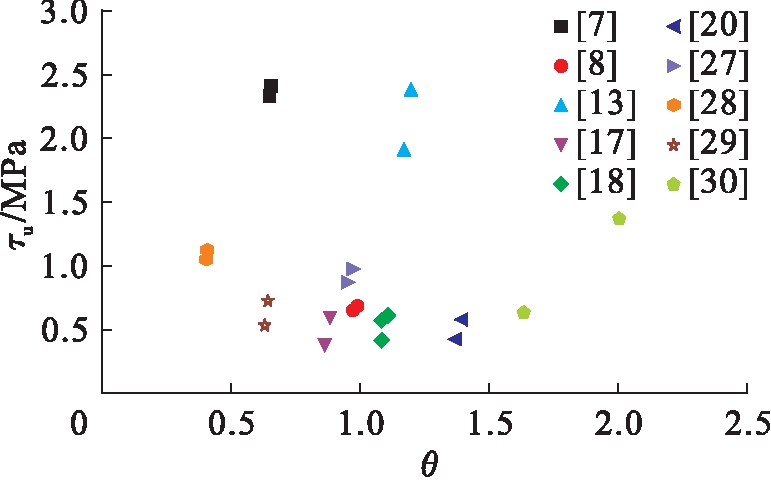
图4 套箍系数与粘结强度的关系
Fig.4 Relationships of confining factor and bond strength
2 极限粘结强度统一计算方法
2.1 极限粘结强度计算模型
不同学者对钢管混凝土极限粘结强度展开了大量的研究,取得了不同的结果.
2.1.1 圆钢管混凝土
1) 蔡绍怀[13]极限粘结强度计算模型为
(1)
式中:τu为极限粘结强度;fcu为混凝土抗压强度.
2) 康希良[14]极限粘结强度计算模型为
29.090 49α+0.034 39θ-7.360 37]
(2)
式中:γ为不确定影响系数,取0.96;k为钢管表面状况影响系数,建议取1.3;ft为混凝土抗拉强度;Le/d为长径比;d/t为径厚比;α为含钢率;θ为套箍系数.
3) Brett等[15]极限粘结强度计算模型为
τu=2.109-0.026d/t
(3)
4) 刘玉茜[16]极限粘结强度计算模型为
τu=1.485 7-0.021 7d/t
(4)
5) 胡波等[17]极限粘结强度计算模型为
(5)
式中:ks为截面影响系数,取2.0;kf为表面粗糙程度影响系数,取1.25;ke为荷载偏心率影响系数,取1.0.
6) 张晓天[18]极限粘结强度计算模型为
τu=0.05ft(-0.030 1L/d+0.006 1d/t+
35.349 9α+1.010 5θ-0.729 4)
(6)
为了验证以上各计算模型的精确性,利用本文搜集的457个圆钢管混凝土试件的粘结滑移试验数据分别按已有的各计算模型进行计算,并将计算结果与试验数据进行对比分析,结果如图5~10所示.
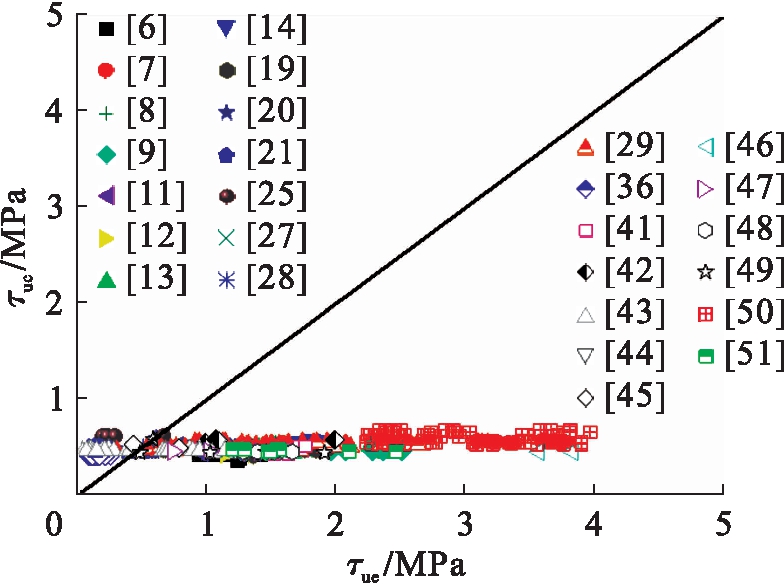
图5 公式(1)对比分析
Fig.5 Comparative analysis of formula (1)
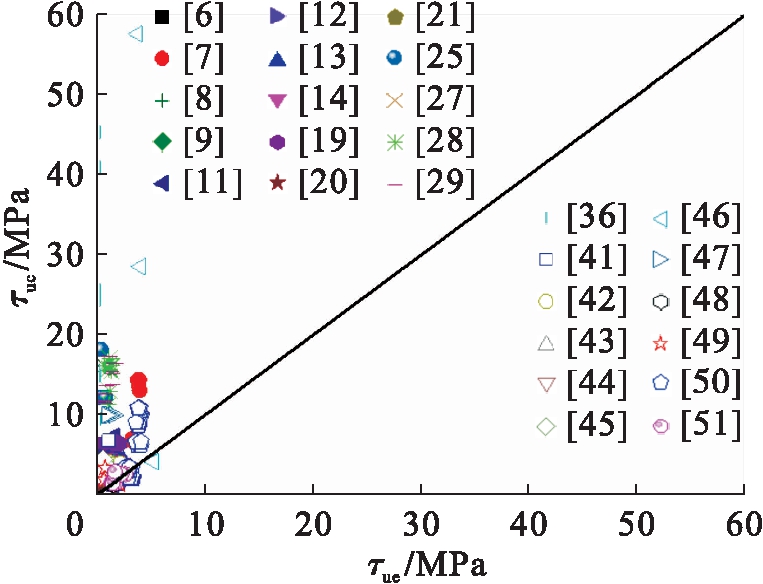
图6 公式(2)对比分析
Fig.6 Comparative analysis of formula (2)
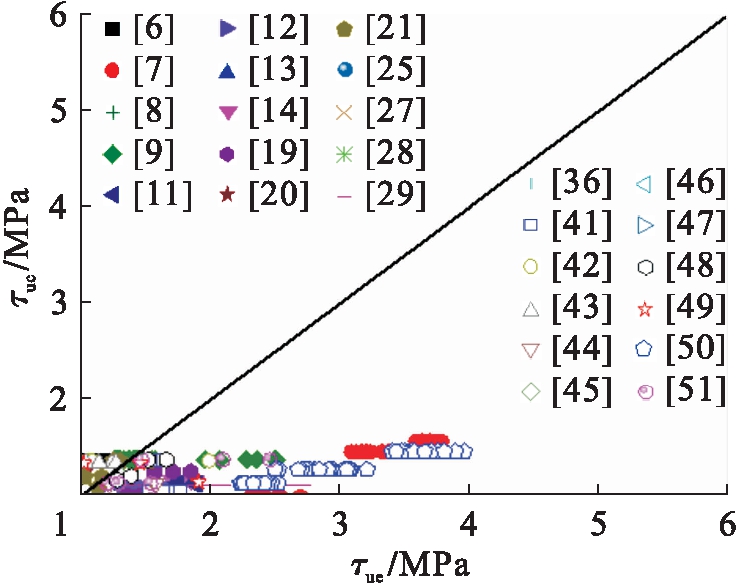
图7 公式(3)对比分析
Fig.7 Comparative analysis of formula (3)
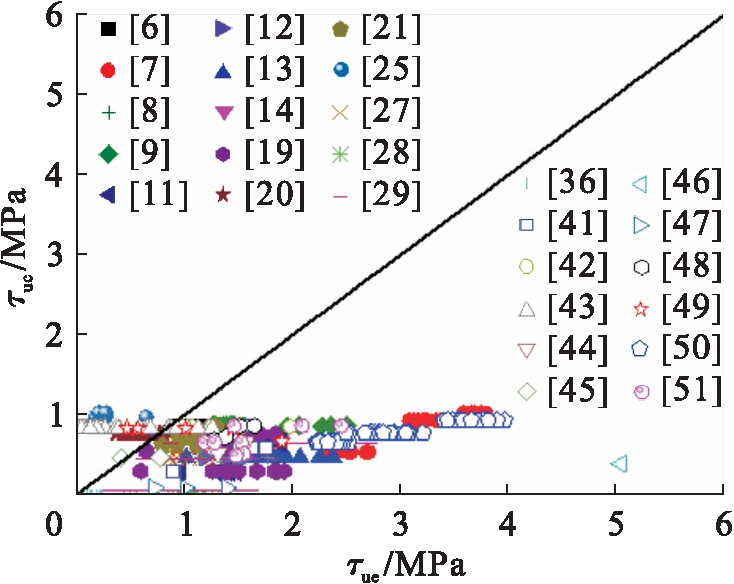
图8 公式(4)对比分析
Fig.8 Comparative analysis of formula (4)
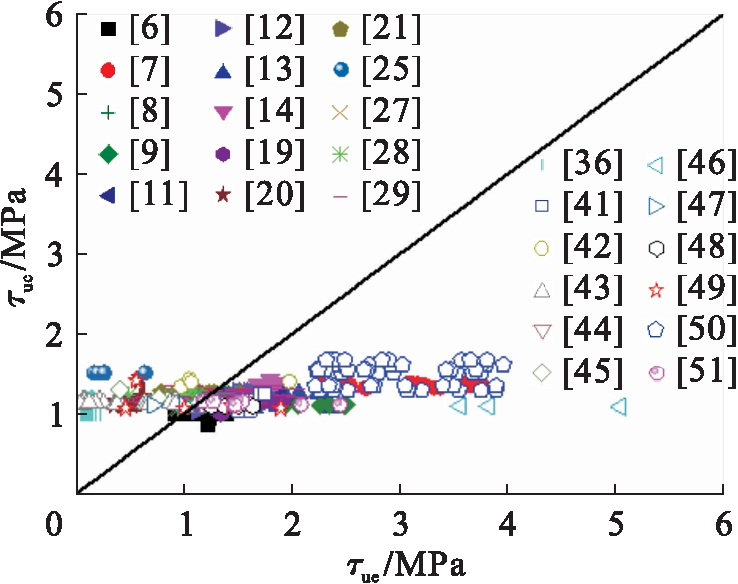
图9 公式(5)对比分析
Fig.9 Comparative analysis of formula (5)
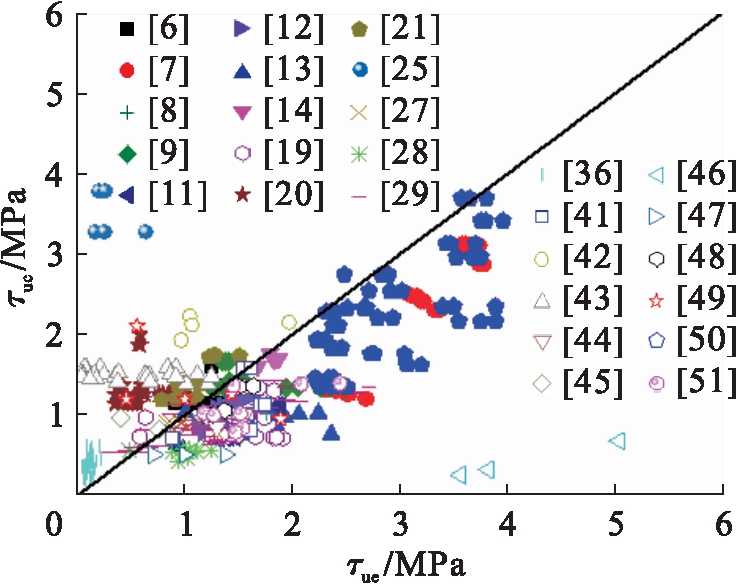
图10 公式(6)对比分析
Fig.10 Comparative analysis of formula (6)
图5~10分别给出了式(1)~(6)计算的圆钢管混凝土极限粘结强度τuc与试验值τue的比较.分析表明:式(1)中,τuc/τue的平均值、均方差分别为0.330、0.061;式(2)中,τuc/τue的平均值、均方差分别为4.424、9.768;式(3)中,τuc/τue的平均值、均方差分别为0.640、0.586;式(4)中,τuc/τue的平均值、均方差分别为0.351、0.489;式(5)中,τuc/τue的平均值、均方差分别为0.826、0.151;式(6)中,τuc/τue的平均值、均方差分别为0.877、0.717.总体上现有圆钢管混凝土极限粘结强度计算模型的理论计算值与试验值吻合不理想,不适合工程应用.
2.1.2 方钢管混凝土
1) 刘玉茜[16]极限粘结强度计算模型为
τu=0.891 42-0.013 02B/t
(7)
式中,B/t为宽厚比.
2) 胡波等[17]极限粘结强度计算模型为
(8)
式中:ks为截面影响系数,取1.0;kf为表面粗糙程度影响系数,取1.25;ke为荷载偏心率影响系数,取1.0.
3) 张晓天[18]极限粘结强度计算模型为
τu=0.06(0.021 4L/B-
0.025 3B/t+3.092 7)
(9)
式中,L/B为长宽比.
4) 仵建斌[19]极限粘结强度计算模型为
τu=(-0.127 7+0.001L/B-
0.149 5t/B+0.285 2θ)ft
(10)
式中,t/B为厚宽比.
5) 滑程耀[20]极限粘结强度计算模型为
(11)
式中:γ为不确定影响系数,取1.1;k为钢管表面状况影响系数,建议取1.3.
6) 赵耀灿等[21]极限粘结强度计算模型为
(12)
式中:α为表面系数,取1.3;β为安全系数,取1.26.
7) 张丽[22]极限粘结强度计算模型为
τu=1.485 7-0.021 7B/t
(13)
为了验证以上各计算模型的精确性,利用本文搜集的166个方钢管混凝土试件粘结滑移的试验数据分别按已有的各计算模型进行计算,并将计算结果与试验数据进行对比分析,结果如图11~17所示.
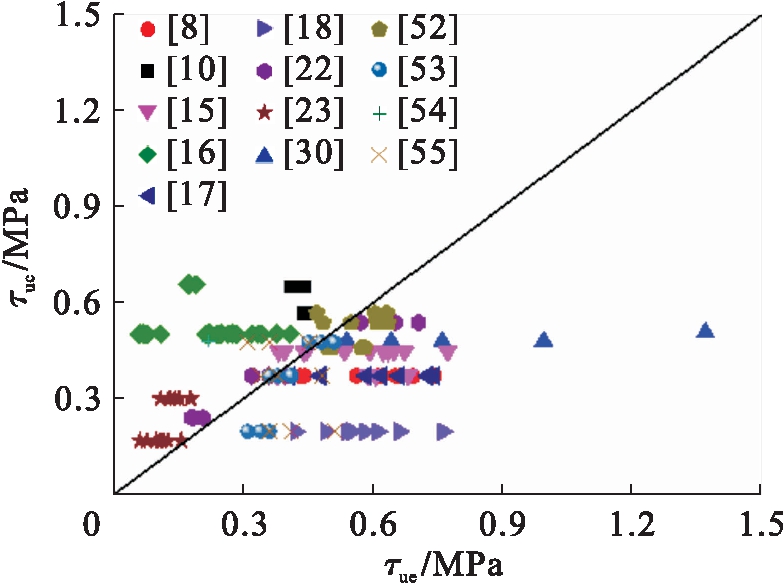
图11 公式(7)对比分析
Fig.11 Comparative analysis of formula (7)
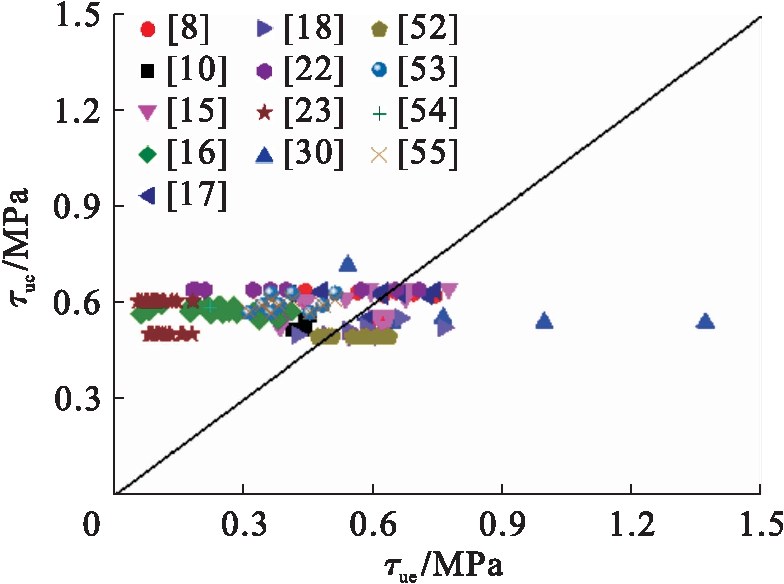
图12 公式(8)对比分析
Fig.12 Comparative analysis of formula (8)
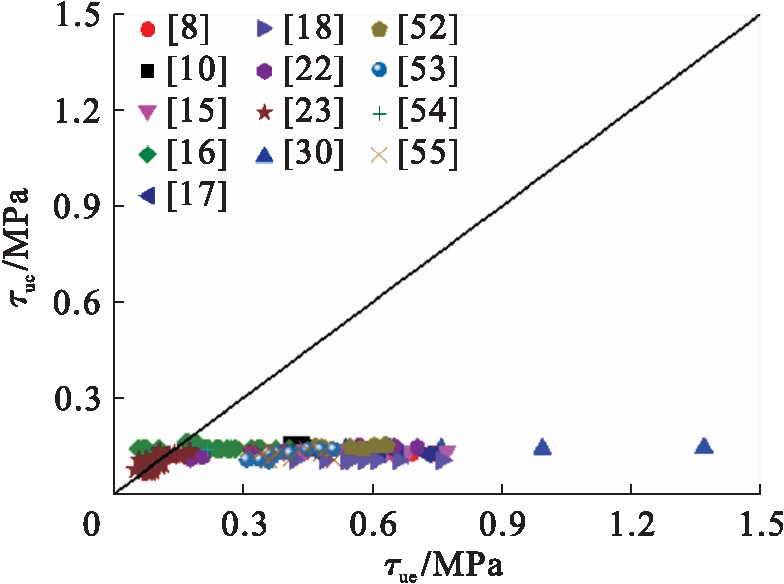
图13 公式(9)对比分析
Fig.13 Comparative analysis of formula (9)
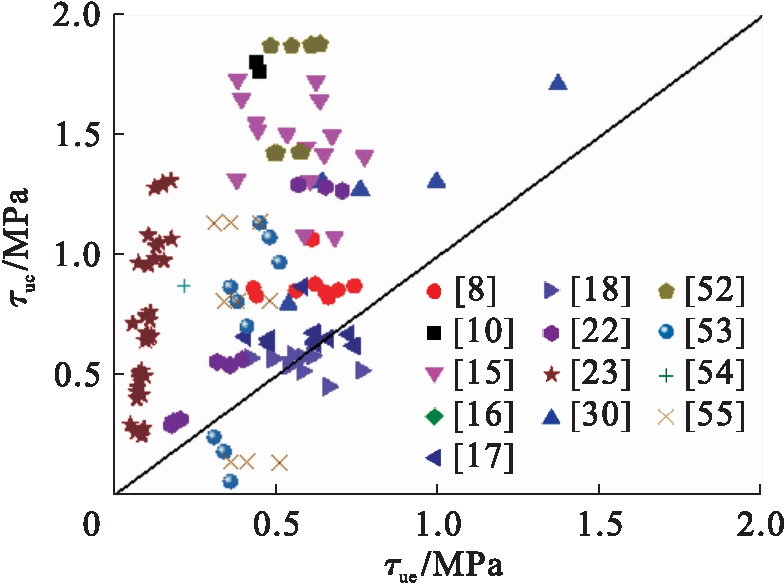
图14 公式(10)对比分析
Fig.14 Comparative analysis of formula (10)
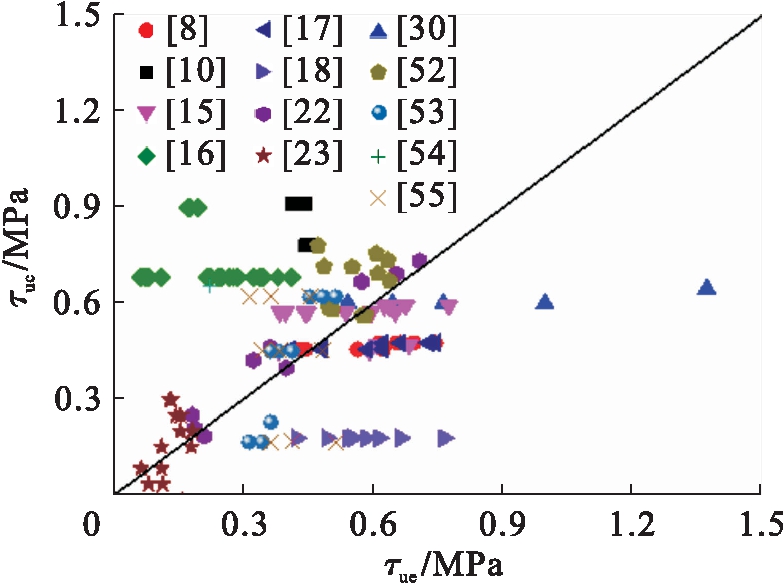
图15 公式(11)对比分析
Fig.15 Comparative analysis of formula (11)
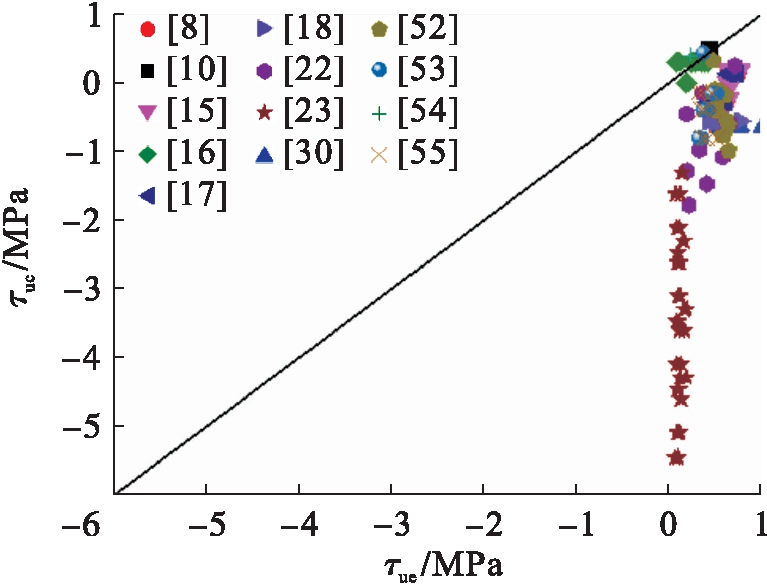
图16 公式(12)对比分析
Fig.16 Comparative analysis of formula (12)
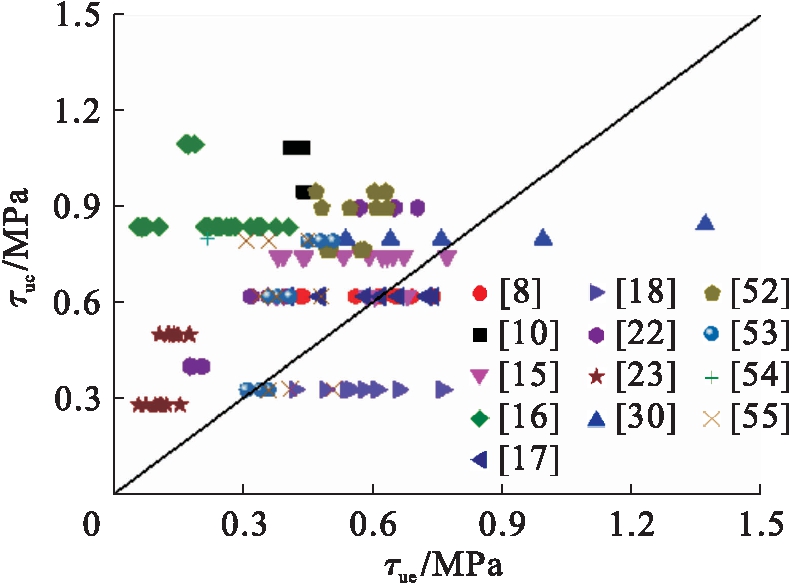
图17 公式(13)对比分析
Fig.17 Comparative analysis of formula (13)
图11~17分别给出了式(7)~(13)计算的方钢管混凝土极限粘结强度τuc与试验值τue的比较.分析表明:式(7)中,τuc/τue的平均值、均方差分别为3.362、0.770;式(8)中,τuc/τue的平均值、均方差分别为0.337、0.022;式(9)中,τuc/τue的平均值、均方差分别为1.107、0.372;式(10)中,τuc/τue的平均值、均方差分别为-1.936、1.441;式(11)中,τuc/τue的平均值、均方差分别为0.955、0.208;式(12)中,τuc/τue的平均值、均方差分别为1.591、0.346;式(13)中,τuc/τue的平均值、均方差分别为1.466、0.051.总体上现有方钢管混凝土极限粘结强度计算模型的理论计算值与试验值吻合不理想,不适合工程应用.
2.2 极限粘结强度统一计算模型
通过对粘结强度影响因素的分析,发现大多数试验试件为轴压短柱,偏压变形造成的界面挤压力的增加极小,因此,长径(宽)比是次要的影响因素.故钢管混凝土粘结强度的决定因素主要是径(宽)厚比和内填混凝土强度.通过对457个圆钢管混凝土试件及166个方钢管混凝土试件试验数据的拟合得出圆钢管混凝土及方钢管混凝土极限粘结强度的统一计算公式为
(14)
(15)
由于本文所得试验数据有限,依据参考文献试验数据得式(14)计算模型的适用范围为:混凝土强度C20~C100;径厚比20~100;长径比1.3~10;套箍系数0.3~3.3;界面为不经过人工处理的正常情况.式(15)计算模型的适用范围为:混凝土强度C30~C60;宽厚比18~85;长宽比2~15;套箍系数0.5~3.3;界面为不经过人工处理的正常情况.
2.3 试验验证
为了验证极限粘结强度统一计算模型的正确性,使用试验数据进行对比分析验证,验证理论公式的正确性.
图18~19分别给出了式(14)、(15)计算的极限粘结强度τuc与试验值τue的比较.分析表明:圆钢管混凝土极限粘结强度的理论计算值与试验值的比值τuc/τue的平均值、均方差分别为0.984、0.141;方钢管混凝土极限粘结强度的理论计算值与试验值的比值τuc/τue的平均值、均方差分别为0.962、0.187.总体上轴压承载力理论计算值与试验值吻合较好,且总体上偏于安全,适合工程应用.
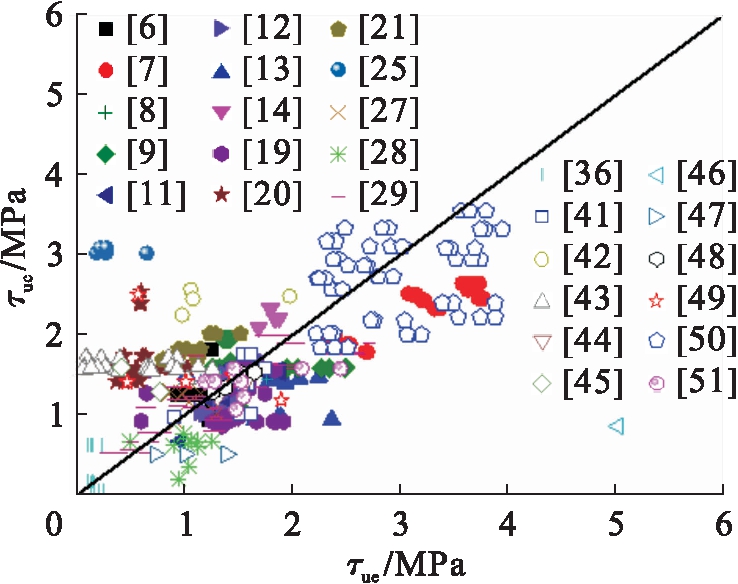
图18 公式(14)对比分析
Fig.18 Comparative analysis of formula (14)
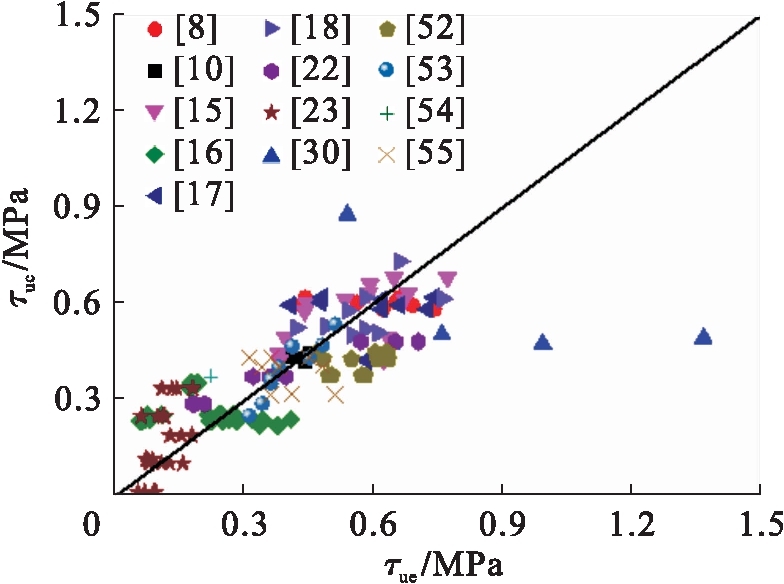
图19 公式(15)对比分析
Fig.19 Comparative analysis of formula (15)
3 结 论
通过以上研究,初步得出以下结论:
1) 钢管混凝土的极限粘结强度与长径(宽)比、套箍系数呈正比例关系,与径(宽)厚比呈反比例关系,混凝土强度的影响尚未完全确定.
2) 已有的钢管混凝土极限粘结强度的计算模型与试验值吻合不理想,不适合工程应用.
3) 界面未经人工处理的钢管混凝土的径(宽)厚比和内填混凝土强度是决定极限粘结强度的决定因素.
4) 将457个圆钢管混凝土试件及166个方钢管混凝土试件的试验数据与极限粘结强度统一计算模型的理论计算值进行了对比分析,两者吻合较好,τuc/τue的平均值、均方差分别为0.984、0.141及0.962、0.187,证明了极限粘结强度统一计算模型的正确性.
[1]武斌,谭卓英,车媛.圆钢管混凝土抗弯刚度研究 [J].混凝土,2018(12):34-39.
(WU Bin,TAN Zhuo-ying,CHE Yuan.Study on flexural stiffness of concrte-filled steel tubes with circular sections [J].Concrete,2018(12):34-39.)
[2]武斌,谭卓英,顾威.圆钢管混凝土受弯构件中性层偏移规律及承载力研究 [J].四川建筑科学研究,2017,43(5):17-21.
(WU Bin,TAN Zhuo-ying,GU Wei.Study on neutral layer migration law and flexural capacity about the concrete filled circular steel tubular flexural members [J].Sichuan Building Science,2017,43(5):17-21.)
[3]武斌,谭卓英,王舜,等.钢管赤泥混凝土粘结滑移影响因素 [J].沈阳工业大学学报,2021,43(1):98-104.
(WU Bin,TAN Zhuo-ying,WANG Shun,et al.Influencing factors of bond slip of red mud concrete filled steel tubes [J].Journal of Shenyang University of Technology,2021,43(1):98-104.)
[4]Wu B,Tan Z Y,Li F,et al.Influence of red mud proportion on circular concrete-filled steel tubular short columns [J].Advances in Materials Science and Engineering,2020(8):1-11.
[5]Virdi K S,Dowling P J.Bond strength in concrete filled circular steel tubes [J].IABSE Periodica,1975,3:125-139.
[6]池建军.钢管混凝土界面抗剪粘结性能的试验研究与有限元分析 [D].长沙:长沙理工大学,2004.
(CHI Jian-jun.Experimental study and FEA of the shear bond behaviors at the interface of concrete-filled steel tube [D].Changsha:Changsha University of Science & Technology,2004.)
[7]丁庆军,周孝军,牟廷敏,等.钢纤维增韧微膨胀钢管混凝土界面粘结性能研究 [J].功能材料,2013,44(6):809-813.
(DING Qing-jun,ZHOU Xiao-jun,MU Ting-min,et al.Bond properties at interface of steel fiber reinforced micro-expansion concrete filled steel tube [J].Journal of Functional Materials,2013,44(6):809-813.)
[8]陈宗平,徐金俊,郑华海.钢![]() 再生混凝土界面粘结机制及强度计算方法 [J].应用基础与工程科学学报,2014,22(2):350-363.
再生混凝土界面粘结机制及强度计算方法 [J].应用基础与工程科学学报,2014,22(2):350-363.
(CHEN Zong-ping,XU Jin-jun,ZHENG Hua-hai.Performance of interface bond mechanism and method of strength calculation between steel and recycled aggregate concrete [J].Journal of Basic Science and Engineering,2014,22(2):350-363.)
[9]傅中秋,吉伯海,陈晶晶,等.钢管轻集料混凝土组合界面黏结滑移性能 [J].河海大学学报(自然科学版),2009,37(3):317-322.
(FU Zhong-qiu,JI Bo-hai,CHEN Jing-jing,et al.Mechanical behaviors of bond slip at interface of lightweight aggregate concrete for steel tubes [J].Journal of Hohai University (Natural Sciences),2009,37(3):317-322.)
[10]申鑫.方钢管混凝土粘结性能试验研究 [D].天津:天津大学,2007.
(SHEN Xin.Experimental research on bond perfor-mance of concrete filled square steel tube [D].Tianjin:Tianjin University,2007.)
[11]黄晖,叶燕华,杜艳静,等.钢管自密实混凝土黏结滑移性能试验研究 [J].混凝土,2010(4):23-27.
(HUANG Hui,YE Yan-hua,DU Yan-jing,et al.Experimental study on the bond-slip between steel tube and self-compacting concrete [J].Concrete,2010(4):23-27.)
[12]武斌,谭卓英,王奇,等.圆钢管赤泥混凝土粘结滑移性能试验研究 [J].河南理工大学学报(自然科学版),2019,38(4):148-153.
(WU Bin,TAN Zhuo-ying,WANG Qi,et al.Experimental research on the bond-slip behavior of circular steel tubes filled with red mud concrete [J].Journal of Henan Polytechnic University (Natural Science),2019,38(4):148-153.)
[13]蔡绍怀.现代钢管混凝土结构 [M].北京:人民交通出版社,2003.
(CAI Shao-huai.Modern concrete filled steel tube structure [M].Beijing:People’s Communications Press,2003.)
[14]康希良.钢管混凝土组合力学性能及粘结滑移性能研究 [D].西安:西安建筑科技大学,2008.
(KANG Xi-liang.Study on compositing mechanical performance and bond slip performance of concrete filled steel tube [D].Xi’an:Xi’an University of Architecture and Technology,2008.)
[15]Brett C G,Cenk T,Jerome F H,et al.Synopsis of studies of the monotonic and cyclic;behavior of concrete-filled steel tube beam [R].Urbana:Department of Civil and Environmental Engineering,University of Illinois at Urbana Champaign,2008.)
[16]刘玉茜.钢管混凝土粘结滑移性能的理论分析及ANSYS程序验证 [D].西安:西安建筑科技大学,2006.
(LIU Yu-qian.Study on the basic theory of bond-slip between steel tube and concrete in CFT structures and numerical simulation by ANSYS program [D].Xi’an:Xi’an University of Architecture and Technology,2006.)
[17]胡波,王建国.钢管与混凝土粘结![]() 滑移相互作用的数值模拟 [J].中国公路学报,2009,22(4):84-91.
滑移相互作用的数值模拟 [J].中国公路学报,2009,22(4):84-91.
(HU Bo,WANG Jian-guo.Numerical simulation on bond-slip behavior of concrete-filled steel tubes [J].China Journal of Highway and Transport,2009,22(4):84-91.)
[18]张晓天.薄壁不锈钢管混凝土粘结滑移性能试验研究 [D].泉州:华侨大学,2017.
(ZHANG Xiao-tian.Experimental study on bond-slip behavior of thin walled concrete-filled stainless steel tube [D].Quanzhou:Huaqiao University,2017.)
[19]仵建斌.方钢管混凝土结构粘结滑移基本性能研究 [D].西安:西安建筑科技大学,2011.
(WU Jian-bin.Study on the performance of bond-slip between steel shape and concrete in CFSST structures [D].Xi’an:Xi’an University of Architecture and Technology,2011.)
[20]滑程耀.方钢管混凝土界面粘结性能的试验研究与理论分析 [D].西安:西安建筑科技大学,2007.
(HUA Cheng-yao.Experimental and theoretical study on the bond properties at the interface of concrete-filled square steel tubes [D].Xi’an:Xi’an University of Architecture and Technology,2007.)
[21]赵耀灿,刘佳.方钢管混凝土粘结强度的计算方法 [J].科技信息,2011(5):732-733.
(ZHAO Yao-can,LIU Jia.The compute method of concrete filled square steel tube bond stress [J].Science & Technology Information,2011(5):732-733.)
[22]张丽.钢管混凝土粘结:滑移性能试验研究及性能分析 [D].兰州:兰州交通大学,2010.
(ZHANG Li.Study on bond-slip performance of concrete filled steel tube and numerical analysis [D].Lanzhou:Lanzhou Jiatong University,2010.)