郑敏利, 马 卉, 杨 琳, 陈金国, 吴 迪
(哈尔滨理工大学 机械动力工程学院, 哈尔滨 150080)
摘 要:为了研究圆弧刃铣刀动态铣削过程中的过程阻尼情况,通过分析刀具结构的几何参数和工艺参数,对现有的模型进行整合优化,建立了圆弧刃铣刀过程阻尼的动态铣削数学模型.基于改进的数学模型,计算出后刀面侵入体积,并进行大量切削稳定极限实验,得到了高速下的极限切深.同时,应用Matlab和ANSYS软件解算得到铣削模态方程的过程阻尼系数,结合能量平衡方程,给出了淬硬钢耕犁力系数,进而预测极限切深.仿真结果表明,刀具后角和刃口半径对过程阻尼影响显著,预测极限切深与实验结果一致.
关 键 词:过程阻尼; 耕犁力系数; 极限切深; 圆弧刃铣削; 能量平衡法; 动态铣削; ANSYS仿真; 铣削稳定域
切削稳定性是切削领域中重要研究方向之一,切削颤振会影响生产效率和工件表面质量,对切削加工表面质量的预测和控制是优化工艺参数和提高表面质量的关键[1-2].在动态切削中,阻尼对于维持稳定起着非常重要的作用,阻尼来源于两方面:结构阻尼和过程阻尼,其中,结构阻尼是阻尼的主要来源,可以通过模态分析进行求解.由刀具后刀面和工件已加工表面之间相互作用而产生的阻尼称为过程阻尼,过程阻尼的存在会增大系统的稳定性,这一现象在低速切削下尤为明显[3-4].Tlusty和Ismail最先提出,由于过程阻尼的存在,颤振稳定性随着切削速度的降低而增大[5].由于测量阻尼力需要复杂的实验装置,数据采集较难困难,现有文献中数据很少有提到阻尼力.大多数文献中都忽略过程阻尼力的研究[5-8],而采用传统的线性动态模型使得预测出的低速下稳定极限误差较大,因此,建立和分析包含过程阻尼的非线性模型成为近年来学术界的研究热点和难点.
在早期研究中,Altintas和Weck[9]用动态切削力系数修正了过程阻尼模型;Sisson和Kegg[3]、Lee[10]等人研究了由于后刀面挤压工件表面所产生的耕犁力带来的整体阻尼增加对切削过程动态特性的影响;Sisson和Kegg[3]提出对过程阻尼影响最大的工艺参数是在切削速度方向上的刃口半径大小和刀具后角;在近期的研究中,Altintas等人[11]通过大量动态切削实验获得了动态切削力系数;Huang和Wang[12]建立在过程阻尼影响下的立铣刀模型,并对切削机理和过程阻尼机理分别进行时域仿真;李欣等[13]建立计算刀具后刀面与工件振动波纹的侵入面积以及干涉阻力模型,分析过程阻尼对系统稳定性极限的影响;李忠群[14]等考虑了过程阻尼的二自由度切削,建立颤振稳定性预测模型;杜红[15]等针对钛合金材料的特殊性,基于全离散法给出包含过程阻尼颤振影响的动力系统模型.
本文建立铣刀过程阻尼数学模型,提出了环形铣刀后刀面体积的计算方法,用能量法获得耕犁力系数,并带入到动态方程中.用Matlab解算铣削动态方程,获得过程阻尼系数和耕犁力系数,验证了刀具几何形状和切削条件对过程阻尼的影响,仿真结果与实验结果相符.该方法可用于预测不同切削条件下的过程阻尼和铣削稳定域,得到的数据较为满意.
圆弧刃铣刀在加工过程中产生的振动和旋转导致工件材料形成正弦表面,过程阻尼形成机理如图1所示.铣刀后刀面侵入工件,在切削层方向形成挤压力,即在刀具后刀面上形成切向耕犁力![]() 和法向耕犁力
和法向耕犁力![]() ,这就引起了阻尼现象.铣削系统为2自由度柔性系统,在x和y方向上建立正交坐标系,把作用于每齿径向和切向上的过程阻尼力求和即为x和y方向上的阻尼力,记为
,这就引起了阻尼现象.铣削系统为2自由度柔性系统,在x和y方向上建立正交坐标系,把作用于每齿径向和切向上的过程阻尼力求和即为x和y方向上的阻尼力,记为![]() 和
和![]() .引入过程阻尼系数
.引入过程阻尼系数![]() 和
和![]() ,分别表示在x和y方向上阻尼力
,分别表示在x和y方向上阻尼力![]() 和
和![]() 产生的阻尼影响.将该阻尼系数带入系统的运动方程,即更新传递函数.
产生的阻尼影响.将该阻尼系数带入系统的运动方程,即更新传递函数.
图1 过程阻尼形成机理
Fig.1 Formation mechanism of process damping
1.1 动态铣削模型的确定
在经典系统运动方程中加入过程阻尼系数,形成新的阻尼系数ct,则经典运动方程可表示为
![]()
(1)
式中![]() ;
;![]() ;m、c、k分别为系统模态的结构质量、结构阻尼和结构刚度.作用在刀具上的动态切削力Fx和Fy取决于动态切削厚度hj、轴向切深e、径向切深b和刀具几何形状.
;m、c、k分别为系统模态的结构质量、结构阻尼和结构刚度.作用在刀具上的动态切削力Fx和Fy取决于动态切削厚度hj、轴向切深e、径向切深b和刀具几何形状.
每个切削刃形成的切削表面随着前一次切削变化而变化,即当前时刻工件表面波形在上次切削表面上形成,则瞬时切削层厚度可表示为
hj(φ)=Δxsin φj+Δycos φj
(2)
式中,φj为第j个正在参与切削的刀齿与y轴沿顺时针方向的夹角,φj=φ+(j-1)φp-tan β0(1-cos θ),其中,β0为刀具螺旋升角,φp=2π/N,φ=2πnt/60,N为刀具齿数,n为主轴转速,θ为切削刃上某一点的位置角.
将动态切削力表示为
![]()
(3)
式中:Kt为切削力系数;Δx=x-xo,Δy=y-yo,(x,y)和(xo、yo)分别为内调制和外调制;axx、ayy、axy、ayx代表方向系数,受动态位移引起的动态切削力影响[6],其表达式为
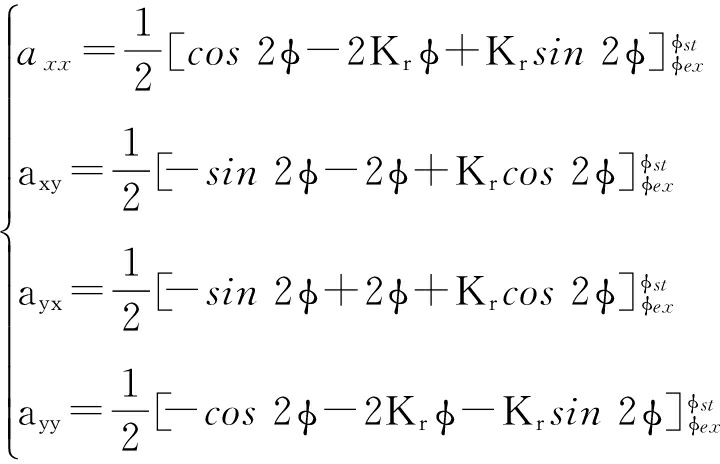
(4)
其中:Kr为轴向切削力系数;φst、φex分别为切入、切出角.
1.2 铣刀稳定性
式(3)经数学变换后,系统动态方程[6]可以在频域表示为
![]()
(5)
式中:A0为切削系统方向系数的矩阵;G为系统传递函数;ωc为系统固有频率;T为刀齿回转周期.
当行列式为0,方程有非零解时,系统稳定性转化为求解系统特征值问题,即
det[I+Λ[G0(iωc)]]=0
(6)
式中,G0(iωc)=A0G(iωc),解得式(6)的特征值[7]用工艺参数表示为
![]()
(7)
最终铣削系统的稳定极限切深可通过传递函数[16]的特征值Λ表示,即
![]()
(8)
![]()
(9)
![]()
(10)
式中:![]() ;
;![]() ;a0=Gxx(iωc)Gyy(iωc)(axxayy-axyayy);a1=axxGxx(iωc)+ayyGyy(iωc);ΛR为特征值Λ的实部部分;κ为特征值虚部和实部的比值;a0、a1为切入切出角度和径向切削力参数的函数,用Gxx、Gyy和axx、ayy、axy、ayx表示;k、ξ分别为铣削系统的结构刚度和阻尼比.引入过程阻尼系数这一参量到系统方程中,由于过程阻尼量尚待确定,则传递函数同样是未知数.反之,若通过实验测得稳定极限alim,则可算得系统特征值,计算过程阻尼,从而预测不同加工条件下的极限切深.
;a0=Gxx(iωc)Gyy(iωc)(axxayy-axyayy);a1=axxGxx(iωc)+ayyGyy(iωc);ΛR为特征值Λ的实部部分;κ为特征值虚部和实部的比值;a0、a1为切入切出角度和径向切削力参数的函数,用Gxx、Gyy和axx、ayy、axy、ayx表示;k、ξ分别为铣削系统的结构刚度和阻尼比.引入过程阻尼系数这一参量到系统方程中,由于过程阻尼量尚待确定,则传递函数同样是未知数.反之,若通过实验测得稳定极限alim,则可算得系统特征值,计算过程阻尼,从而预测不同加工条件下的极限切深.
不同切削速度下的极限切深如图2所示.刀具以一个恒定的频率振动,由于表面斜率降低、波长增大,则随着速度增加,刀具后刀面与工件的挤压体积减小.在较高速度切削时,过程阻尼影响减弱,导致实际稳定极限低于alim;而在低速切削时,过程阻尼影响增大,稳定极限大于alim.用实验测定稳定极限切深alim带入数学模型中,通过逆![]() 稳定分析法计算过程阻尼系数.Altintas和Budak[7]提出,分析稳定极限表达式是为了把实验测定的稳定极限切深alim和过程阻尼系数联系起来,用计算得到的过程阻尼系数来确定模型中的耕犁力系数.
稳定分析法计算过程阻尼系数.Altintas和Budak[7]提出,分析稳定极限表达式是为了把实验测定的稳定极限切深alim和过程阻尼系数联系起来,用计算得到的过程阻尼系数来确定模型中的耕犁力系数.
图2 不同切削速度下的极限切深
Fig.2 Limit cutting depth with different cutting speeds
包含过程阻尼系数的铣削系统传递函数为
![]()
(11)
式中![]() ;ωn为刀齿回转频率;i,j=x,y.
;ωn为刀齿回转频率;i,j=x,y.
在式(7)中带入实验测得稳定极限alim和固有频率ωc,可计算出包括全部阻尼的系统传递函数,即
![]()
(12)
为了确定系统总阻尼比![]() 和
和![]() ,令系统特征值Λ的函数值等于Λexp.由于无法求方程的显式解,因此可通过迭代求解法来获得阻尼比,得到过程阻尼的表达式为
,令系统特征值Λ的函数值等于Λexp.由于无法求方程的显式解,因此可通过迭代求解法来获得阻尼比,得到过程阻尼的表达式为
![]()
(13)
式中,ξs为系统结构阻尼比.
式(12)、(13)建立了过程阻尼系数![]() 和稳定极限alim的函数关系,即已知极限切深alim时,可求解此时的过程阻尼系数,反之,当过程阻尼系数已知时,就可预测此时的极限切深.
和稳定极限alim的函数关系,即已知极限切深alim时,可求解此时的过程阻尼系数,反之,当过程阻尼系数已知时,就可预测此时的极限切深.
预测不同条件的稳定极限切深首先要已知不同条件下的过程阻尼系数,而过程阻尼系数![]() 与压入体积Vj(t,q)和耕犁力系数Kd有关.
与压入体积Vj(t,q)和耕犁力系数Kd有关.
为了预测不同条件下的极限切深alim,首先需要通过实验测量获得具体极限切深下的过程阻尼系数,然后用阻尼能量分析法计算得到耕犁力系数.由于耕犁力系数不随着切削条件改变而改变,可将耕犁力系数用于不同切削条件下的仿真来预测不同条件下的过程阻尼系数和稳定极限.
3.1 确定耕犁力系数Kd
铣刀后刀面与工件已加工波形表面相互挤压形成耕犁力,耕犁力所做功与振动能量的耗散相抵消,使切削厚度上的振动能减小,即形成能量环现象,从而令切削过程趋于稳定,挤压过程如图3所示.
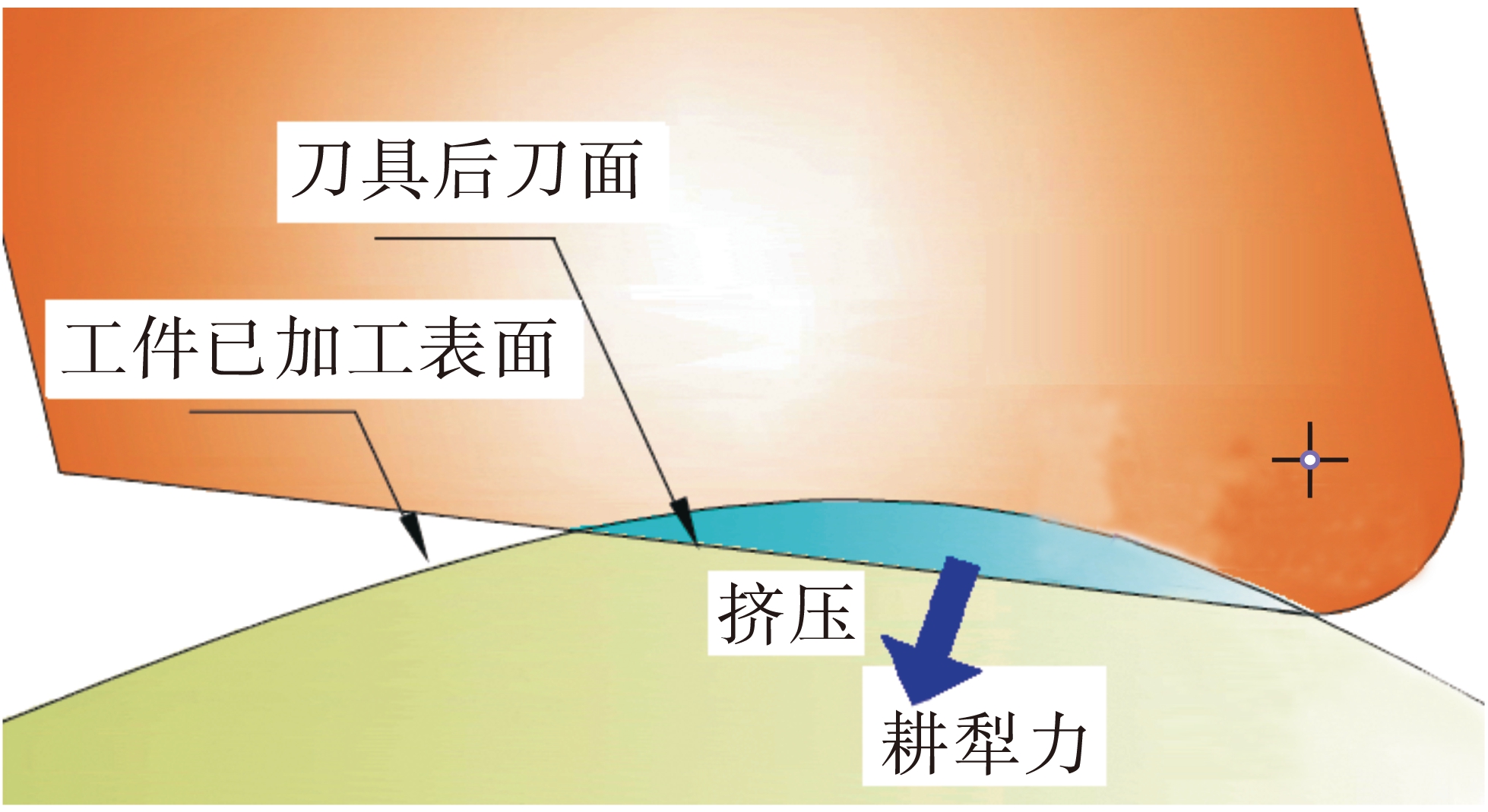
图3 耕犁力挤压后刀面过程
Fig.3 Process of plough force extruding flank face
铣削中耕犁力所做功等于振动耗散的能量,利用这一特性可求解耕犁力系数Kd,因此,需要建立和解算带有耕犁力的数学模型求得过程阻尼系数.在使用能量分析法时,将耕犁力看成一个跟压入体积Vj(t,q)和耕犁力系数Kd有关的函数[10,12].在稳定切削中,刀具系统以频率ωc振动,在x、y方向上的振幅分别为Ax和Ay.将切削刃在轴向上分成若干个微元,作用在切削刃上的耕犁力也在轴向上分成若干个微元,环形铣刀后刀面与工件的接触关系如图4所示.
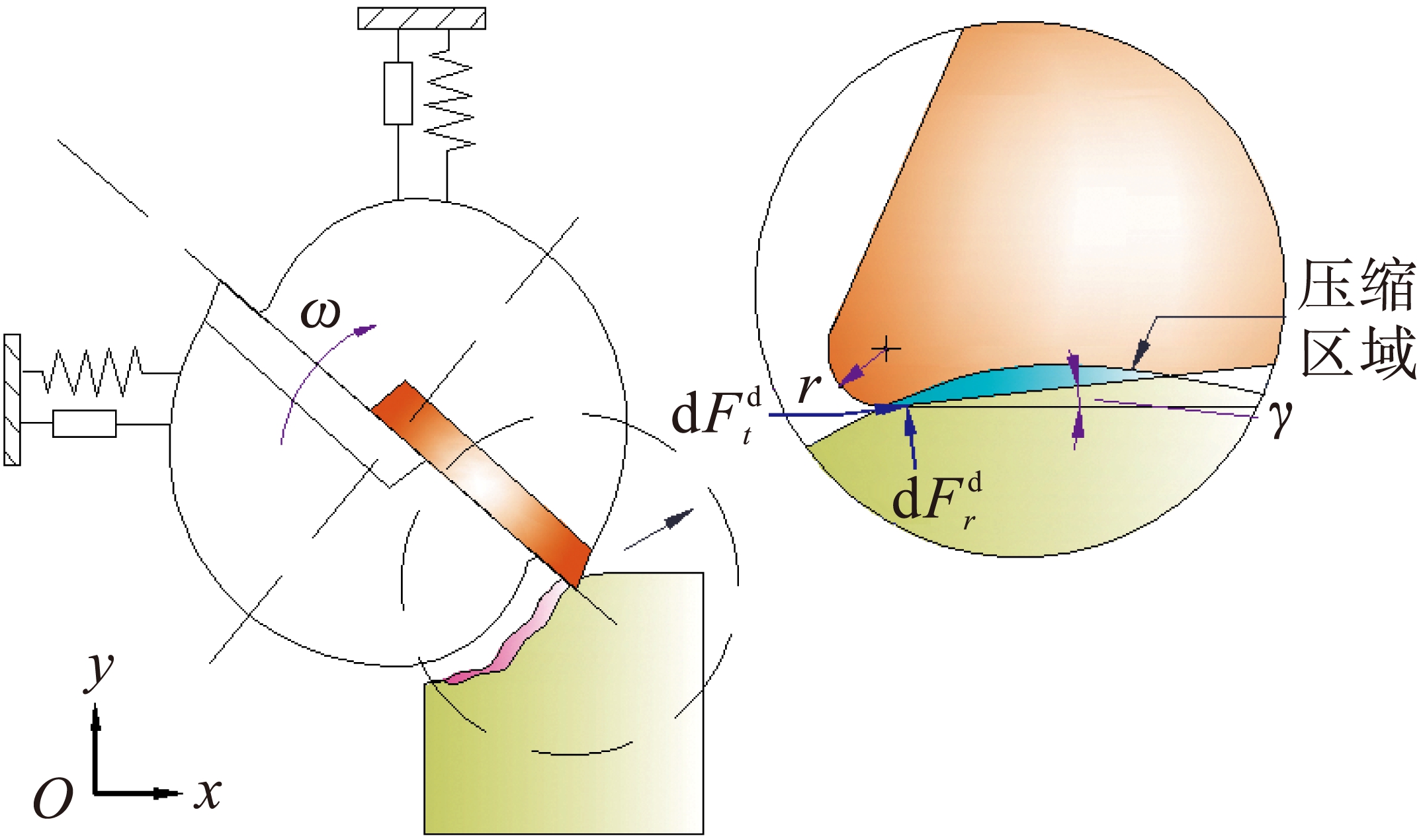
图4 环形铣刀后刀面与工件的接触关系
Fig.4 Corresponding position relationship between cutter blade and workpiece surface
在第j个切削刃上,微分的耕犁力作用于第q个轴向单元,切向力![]() 与法向力
与法向力![]() 表示为
表示为
![]()
(14)
式中:μ为工件和后刀面的接触摩擦系数,通常取0.3[10];Vj(t,q)为第j个刀刃上的单元q在t时刻后刀面的压入体积.由于后刀面![]() 工件表面之间挤压,在切削厚度方向产生阻尼力u,通过轴向s个单元力的求和,得到总阻尼功率
工件表面之间挤压,在切削厚度方向产生阻尼力u,通过轴向s个单元力的求和,得到总阻尼功率![]() ,其表达式为
,其表达式为
![]() γ+μsin γ)·
γ+μsin γ)·
(15)
式中,γ为后角.过程阻尼力耗散![]() 功率为
功率为
![]() φ
φ![]() φ)
φ)![]()
(16)
耕犁力所做功Ec,u与振动耗散的能量Eu相等,即
![]() γ+
γ+
μsin ![]()
式中,Tsp为主轴回转周期.
由式(15)、(16)可得到耕犁力的系数为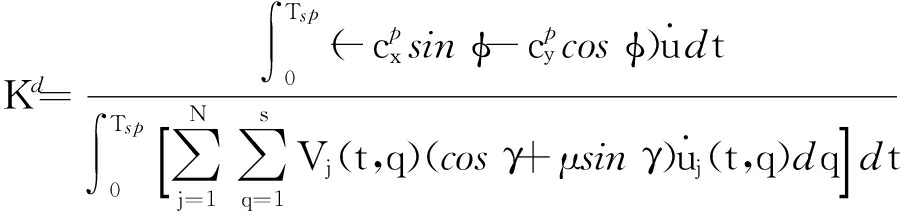
(17)
式(17)建立了过程阻尼系数![]() 、压入体积Vj(t,q)和耕犁力系数Kd的内在函数关系.当给出某一特定条件下的过程阻尼系数和压入体积时,可计算耕犁力系数.而耕犁力系数不随着条件(铣刀几何角度、切削用量等)改变而发生大幅变化,此时可把耕犁力系数看作恒定常数.当压入体积已知时,可用于预测不同切削条件下的过程阻尼系数,进而预测稳定极限.
、压入体积Vj(t,q)和耕犁力系数Kd的内在函数关系.当给出某一特定条件下的过程阻尼系数和压入体积时,可计算耕犁力系数.而耕犁力系数不随着条件(铣刀几何角度、切削用量等)改变而发生大幅变化,此时可把耕犁力系数看作恒定常数.当压入体积已知时,可用于预测不同切削条件下的过程阻尼系数,进而预测稳定极限.
3.2 计算压入体积
建立过程阻尼模型需要计算后刀面压入体积,将刀具切削刃在轴向上分成若干个微小单元,每一单元轴向上的压缩面积乘以单元高度可以得到压入体积.通常根据切削条件、振动频率和刀具几何形状等不同,后刀面上有多种压缩区域形式.刀片在切削厚度方向沿正弦波运动,刀片位置如图5所示.
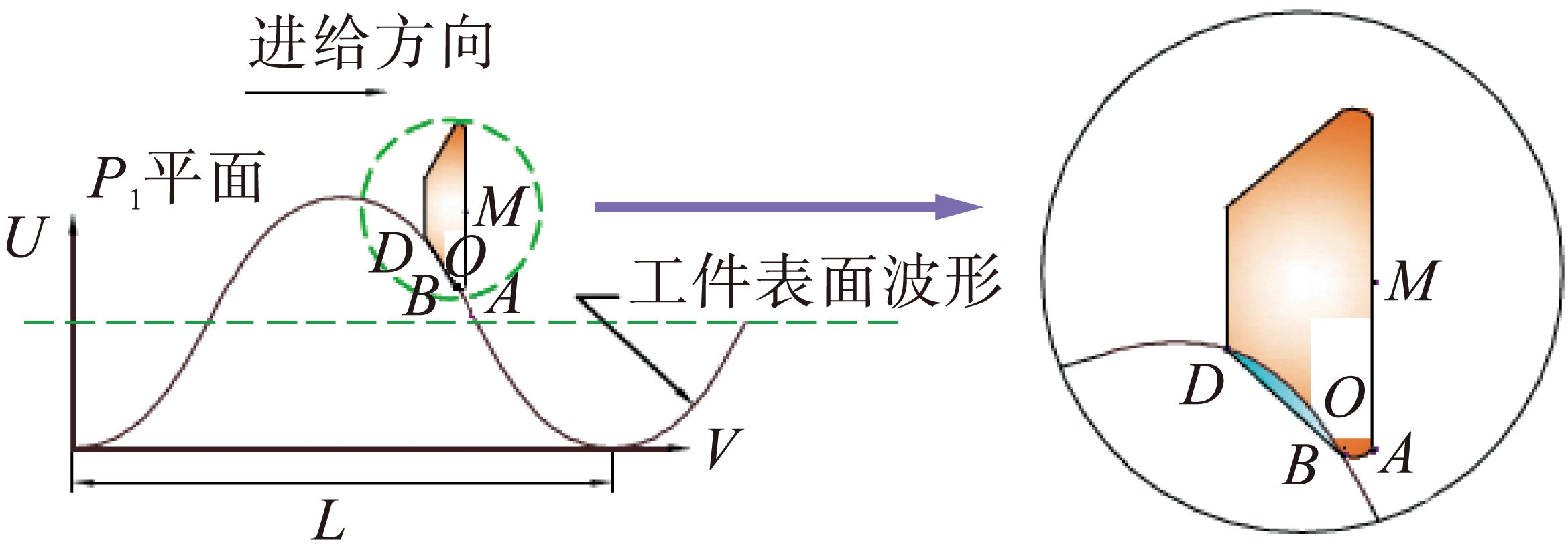
图5 刀片与工件表面的相对位置关系
Fig.5 Contact relationship between flank face and workpiece for ring mill cutter
根据图5给出的环形铣刀后刀面与工件的接触关系求解后刀面压入体积Vj(t,q).刀片在U-V平面上的投影如图6所示,工件已加工表面在P1平面内投影的曲线方程为
![]()
(18)
式中,v(t)为刀片在v轴上的投影值.
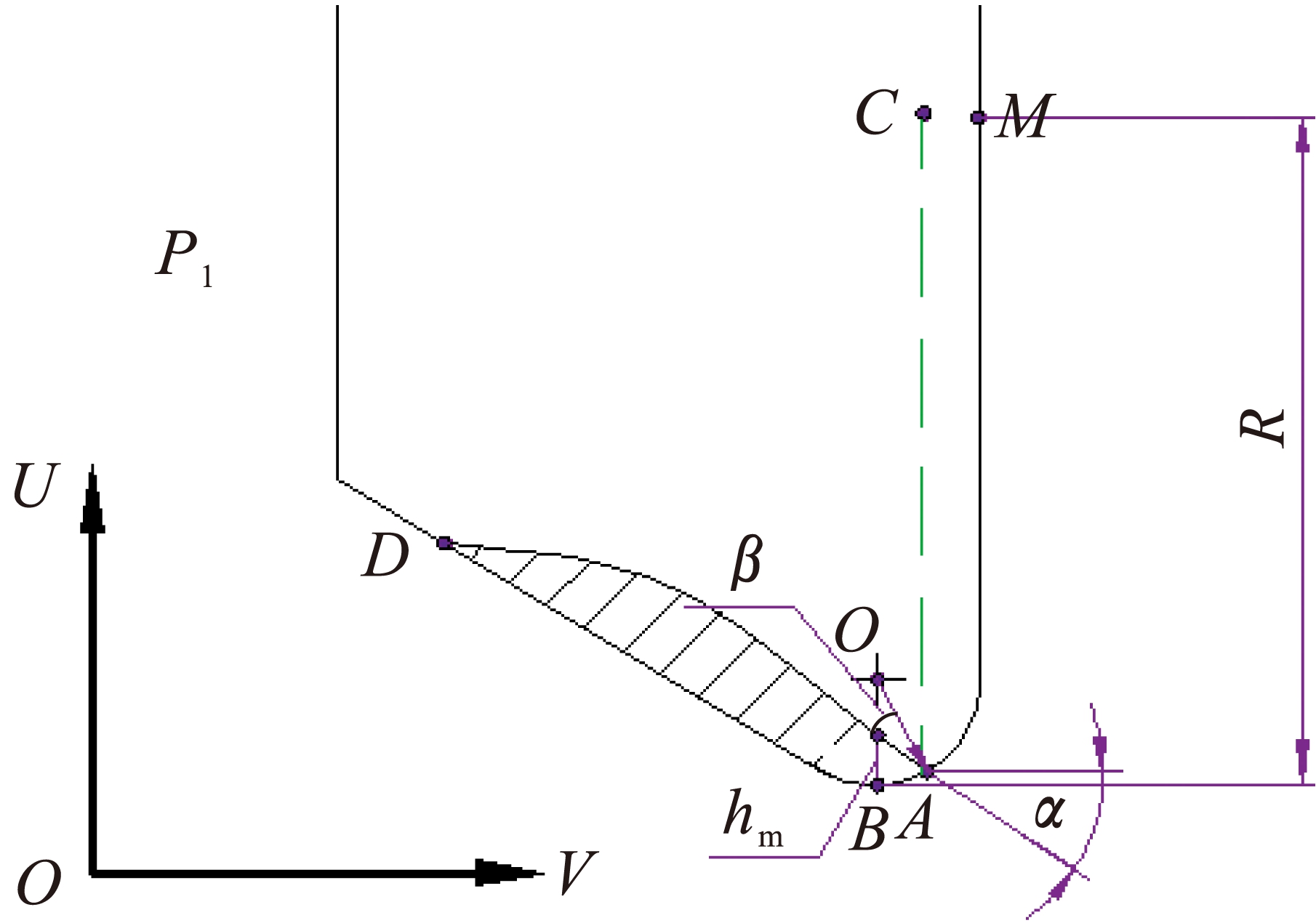
图6 刀片在U-V平面上的投影
Fig.6 Projection of cutter blade on U-V plane
平面内投影的曲线方程为
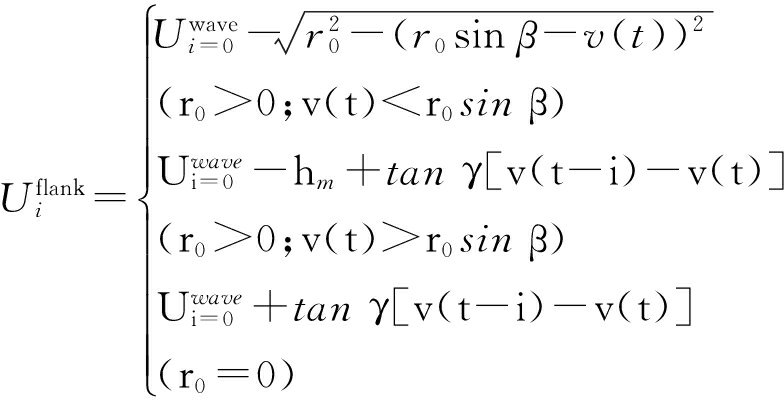
(19)
式中:hm≅![]() ;r0为刀片刃口半径;α、β为分离角,下一时刻工件与切削刃脱离接触.
;r0为刀片刃口半径;α、β为分离角,下一时刻工件与切削刃脱离接触.
刀片在U-V平面上的投影如图6所示,当前点A坐标为![]() ,
,![]() ,V(t)在P1平面上的瞬时截面面积为
,V(t)在P1平面上的瞬时截面面积为
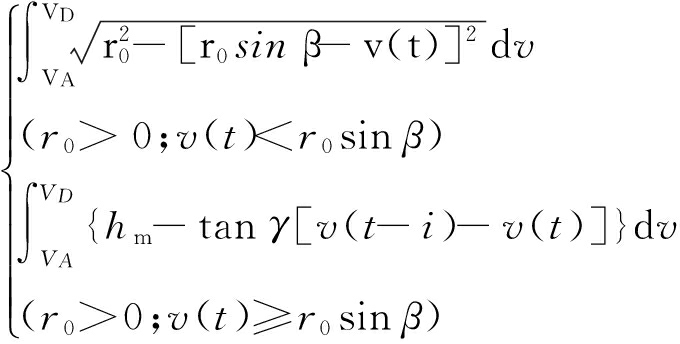
(20)
后刀面和工件间的压缩体积如图7所示,点C坐标为![]() r0+r0cos β,O),R为刀片半径.
r0+r0cos β,O),R为刀片半径.
S(t)沿以点C为圆心,以(R-r0+r0cos β)为半径的圆为轨迹积分,即S(t)沿圆C积分,其中圆C在P2平面内的投影轨迹方程为
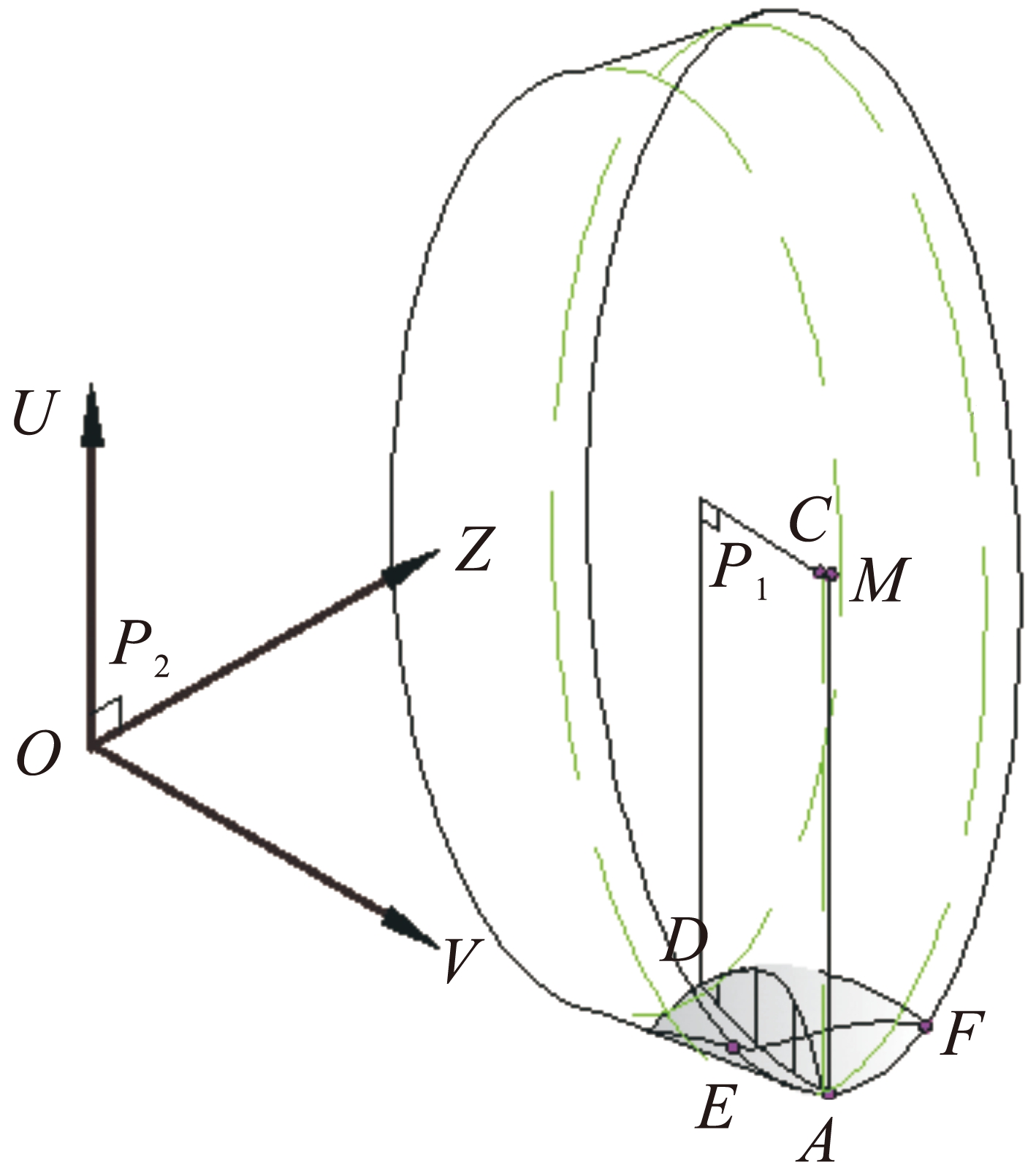
图7 后刀面和工件间的压缩体积
Fig.7 Compression volume betweenflank face and workpieceZ2+(U-UC)2=(R-r0+cos β)2
(21)
后刀面侵入体积
(22)
4.1 实验设计
铣削系统的极限切深反映了系统的稳定域范围,可以通过稳定域来判断铣削加工是否发生颤振,因此需要测定系统极限切削深度,同时观察影响系统极限切深的因素,找到稳定域变化规律.
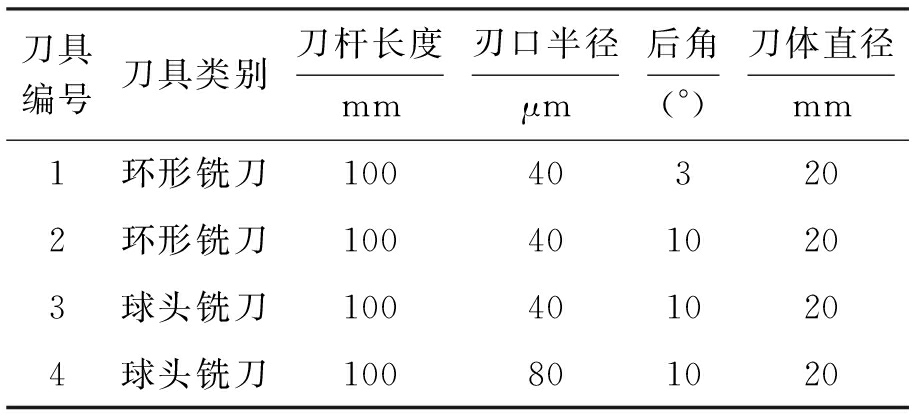
实验设备:机床,大连VDL1000立式加工中心;测试系统,东华动态信号测试分析系统;工件,切削材料为淬硬钢Cr12MoV,洛氏硬度为55HRC,尺寸为75 mm×75 mm×45 mm;刀具,硬质合金刀具4把,前角0°,2齿,具体参数如表1所示.
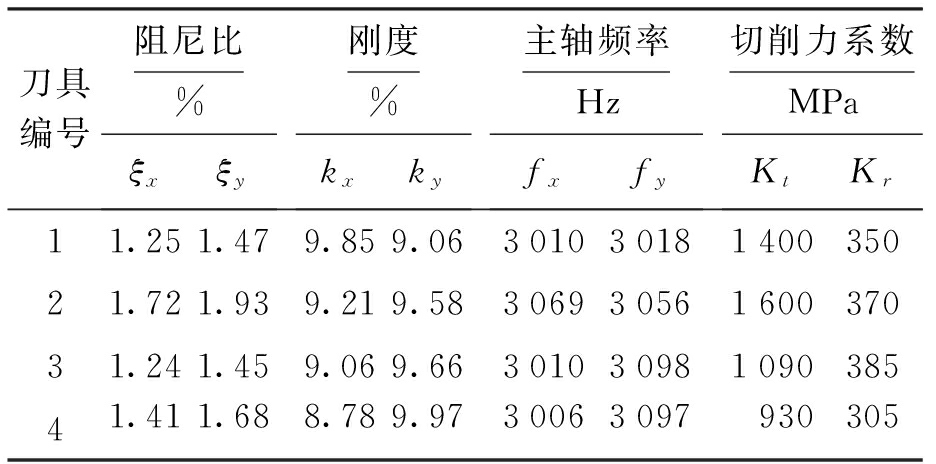
表1 刀具参数
Tab.1 Parameters for tool
实验装置如图8所示,径向切削宽度为0.2 mm,每齿进给量为0.1 mm,顺铣,采用干式切削.刀具![]() 主轴系统结构模态参数如表2所示,模态参数通过力锤敲击获得,切削力系数通过实验法获得[17].
主轴系统结构模态参数如表2所示,模态参数通过力锤敲击获得,切削力系数通过实验法获得[17].

图8 动态铣削实验装置
Fig.8 Device for dynamic milling tests
表2 刀具![]() 主轴系统结构模态参数
主轴系统结构模态参数
Tab.2 Structural modal parameters for tool-spindle system
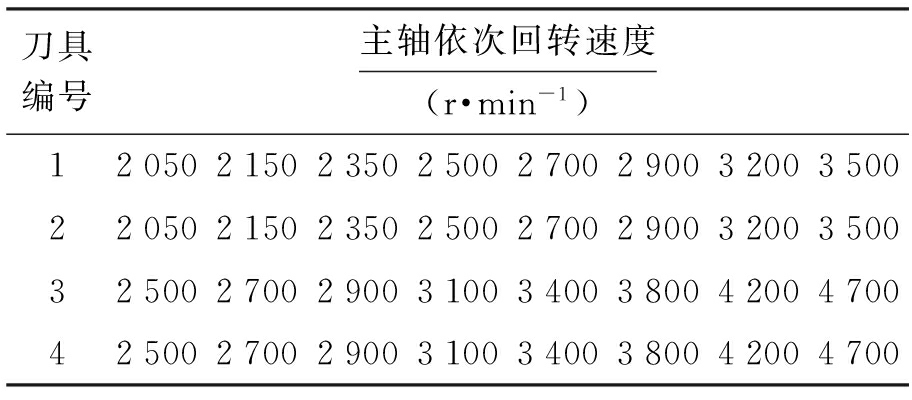
分别测定4把刀具在不同主轴回转速度下的极限切深,主轴速度如表3所示.在切削实验中,逐渐增加轴向切深以确定给定主轴回转速度下的绝对稳定极限,同时采集振幅和振动频率.一般情况下,切深增加到超过理论稳定极限后,振幅会大幅增加.而在过程阻尼影响下,由于后刀面![]() 工件间耕犁力增加,阻尼力增加,抑制了刀具振动,刀具振幅并没有明显增加,因此,用单标准来判别过程阻尼影响下的机床系统是否发生颤振会很困难.在实验中采用观察工件表面振纹和观察输出频谱图来判别颤振是否发生.
工件间耕犁力增加,阻尼力增加,抑制了刀具振动,刀具振幅并没有明显增加,因此,用单标准来判别过程阻尼影响下的机床系统是否发生颤振会很困难.在实验中采用观察工件表面振纹和观察输出频谱图来判别颤振是否发生.
表3 主轴速度
Tab.3 Spindle speed
4.2 实验结果分析
图9为主轴回转速度为2 050 r/min时,不同频谱图和工件表面示意图.可以看到轴向极限切深ap=1 mm时,进给痕迹清晰可见,振纹稳定,频谱图没有明显峰值,此时切削稳定;随着ap增加到2 mm,进给痕迹变小,频谱图峰值较小,此时仍认为切削稳定;当ap=3 mm时,难以辨识进给痕迹,同时频谱图峰值较大,刀具振动增加,此时认为切削不稳定.
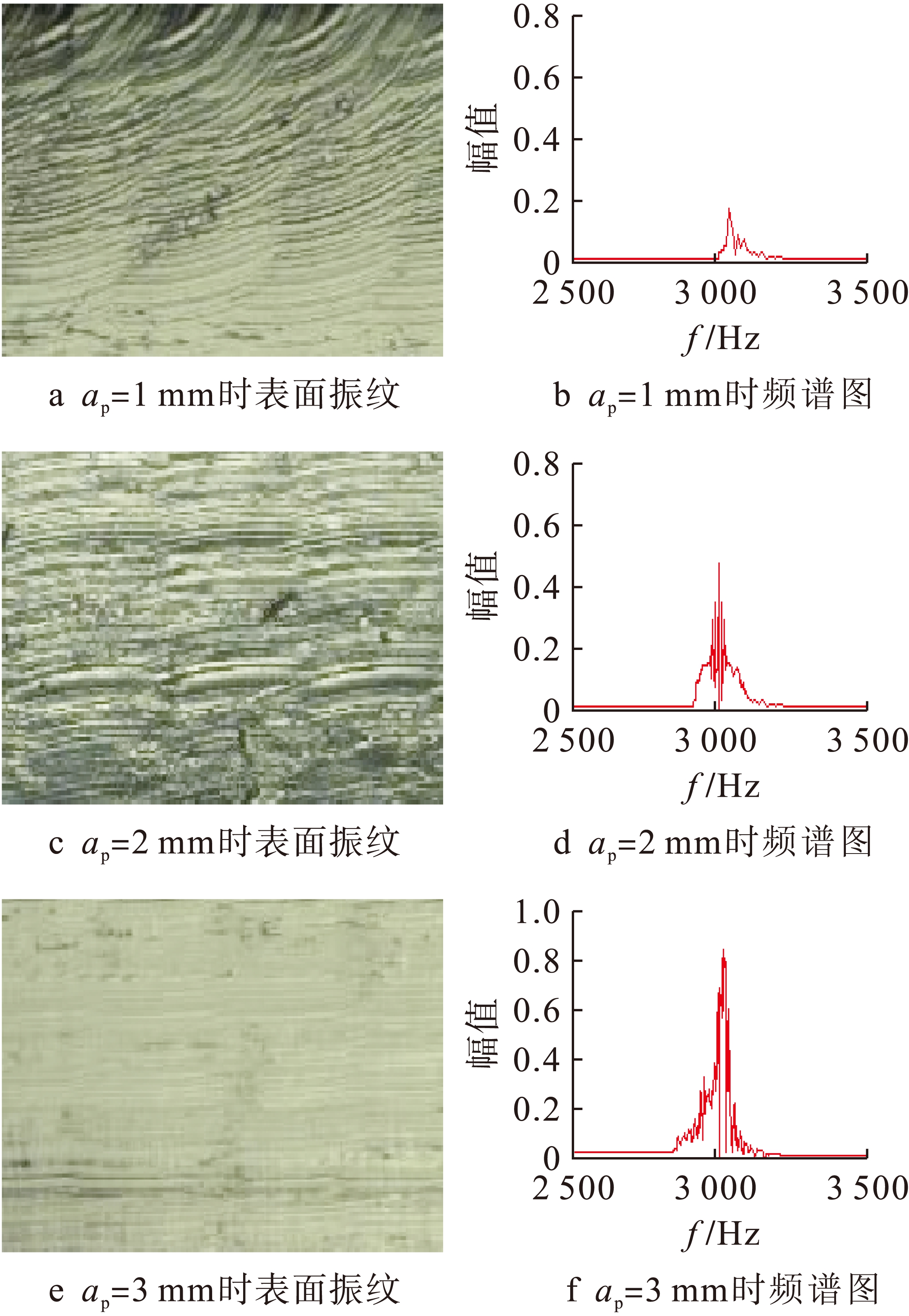
图9 不同频谱及工件表面示意图
Fig.9 Examples for chatter identification
图10为不同主轴转速下的极限稳定切深曲线.图10中,在低速区域可以明显观察到过程阻尼现象,此时系统的稳定极限切深较大;随着主轴回转速度增大,过程阻尼减小,系统稳定性减小,极限切深随之减小;高速时,过程阻尼现象几乎消失,系统极限切深趋于某一固定值.这是由于主轴转速增加时,已加工表面波形被拉伸,导致斜率减小,后刀面对工件表面的挤压减小,导致过程阻尼现象减小.对比10a、b两图可以知,随着后角增大,后刀面压缩工件表面程度减小,过程阻尼现象减弱,极限切深减小.对比10c、d两图知,随着刃口半径增大到80 μm,后刀面与工件表面之间的压缩体积变大,过程阻尼现象更加明显,极限切深增大.
将实验中获得的极限切深带入到式(12)、(13)中,可用Matlab解算得到4把刀具x、y方向上的过程阻尼系数如图11所示.
选取主轴转速为2 500、2 700、2 900 r/min时的过程阻尼系数带入到式(17)中可求解得到淬
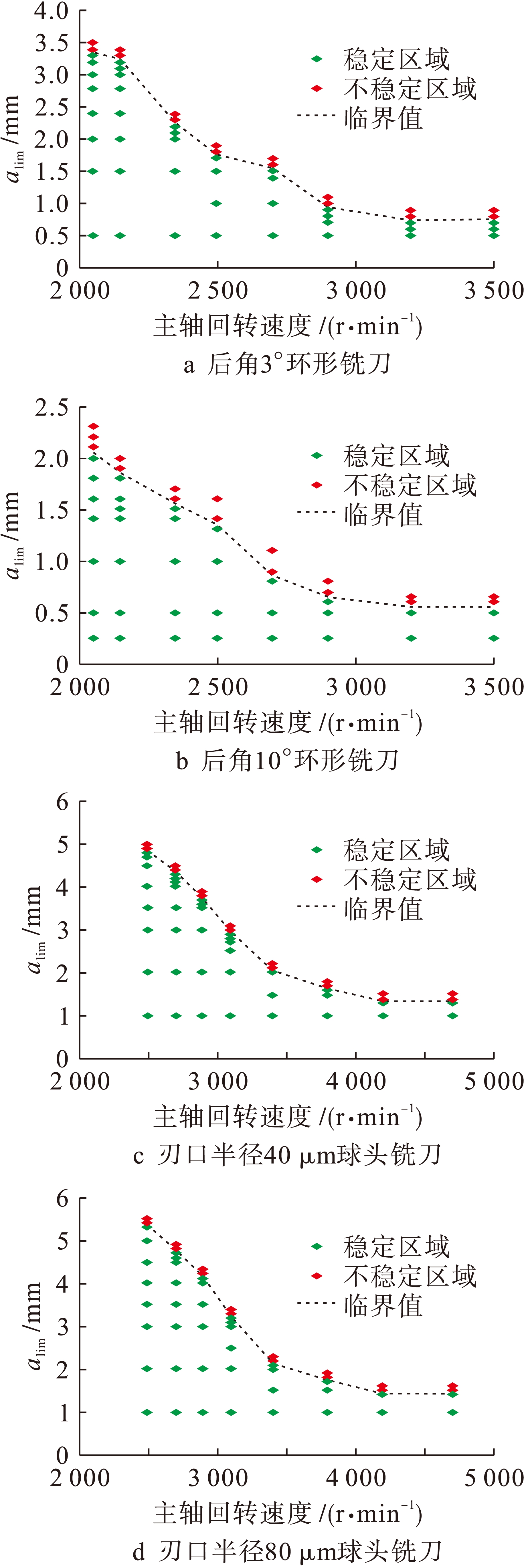
图10 不同主轴转速下的极限稳定切深曲线
Fig.10 Limit stable depth with different spindle speeds
硬钢耕犁力系数Kd曲线如图12所示.观察图12可知,主轴转速、轴向切深、刃口半径和后刀面形状改变时,耕犁力系数无明显变化.
选取后角3°环形铣刀的实验极限切深与Matlab仿真结果进行对比结果如图13所示.由图可知,在传统铣削系统模型中,系统无过程阻尼影响,主轴回转转速逐渐增大时,稳定极限切深无大幅变化;在含过程阻尼铣削系统模型中,由于过程阻尼影响,导致低速下系统极限切深明显增大,铣削系统稳定域增大;随着主轴转速增加,过程阻尼逐渐减小,高速时无法观测到过程阻尼现象,含有过程阻尼的仿真曲线和不含过程阻尼的仿真曲线在高速区域几乎重叠,仿真结果与实验结果相符.
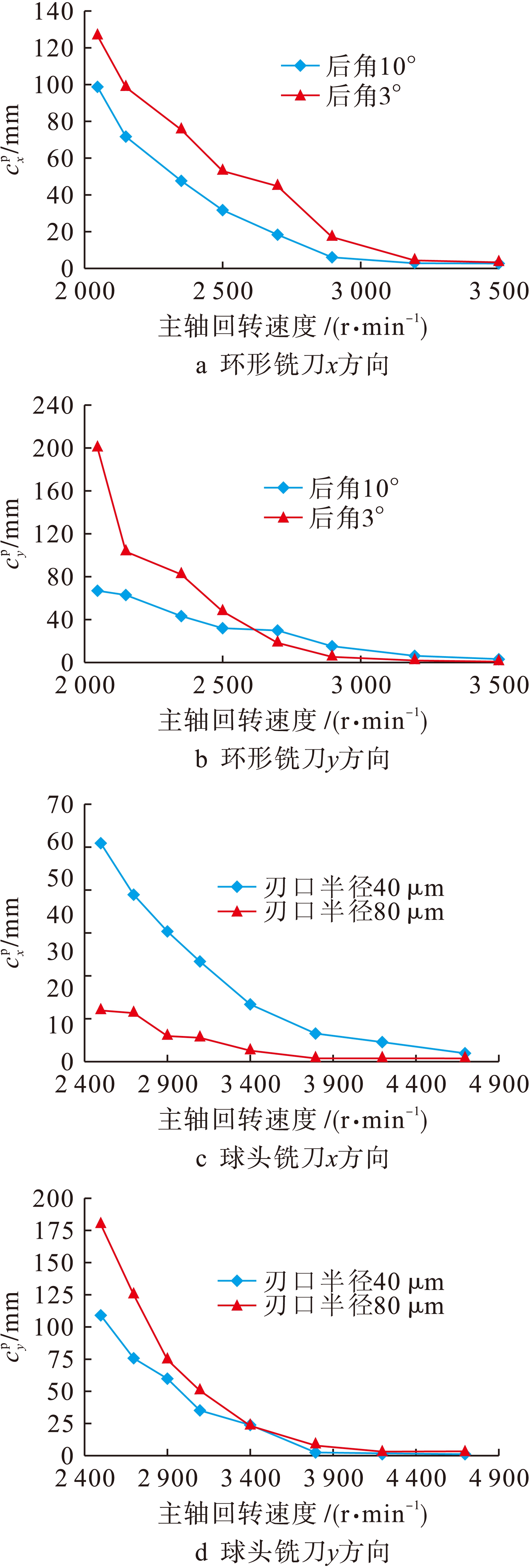
图11 不同主轴转速下的过程阻尼系数曲线
Fig.11 Process damping coefficient with different spindle speeds
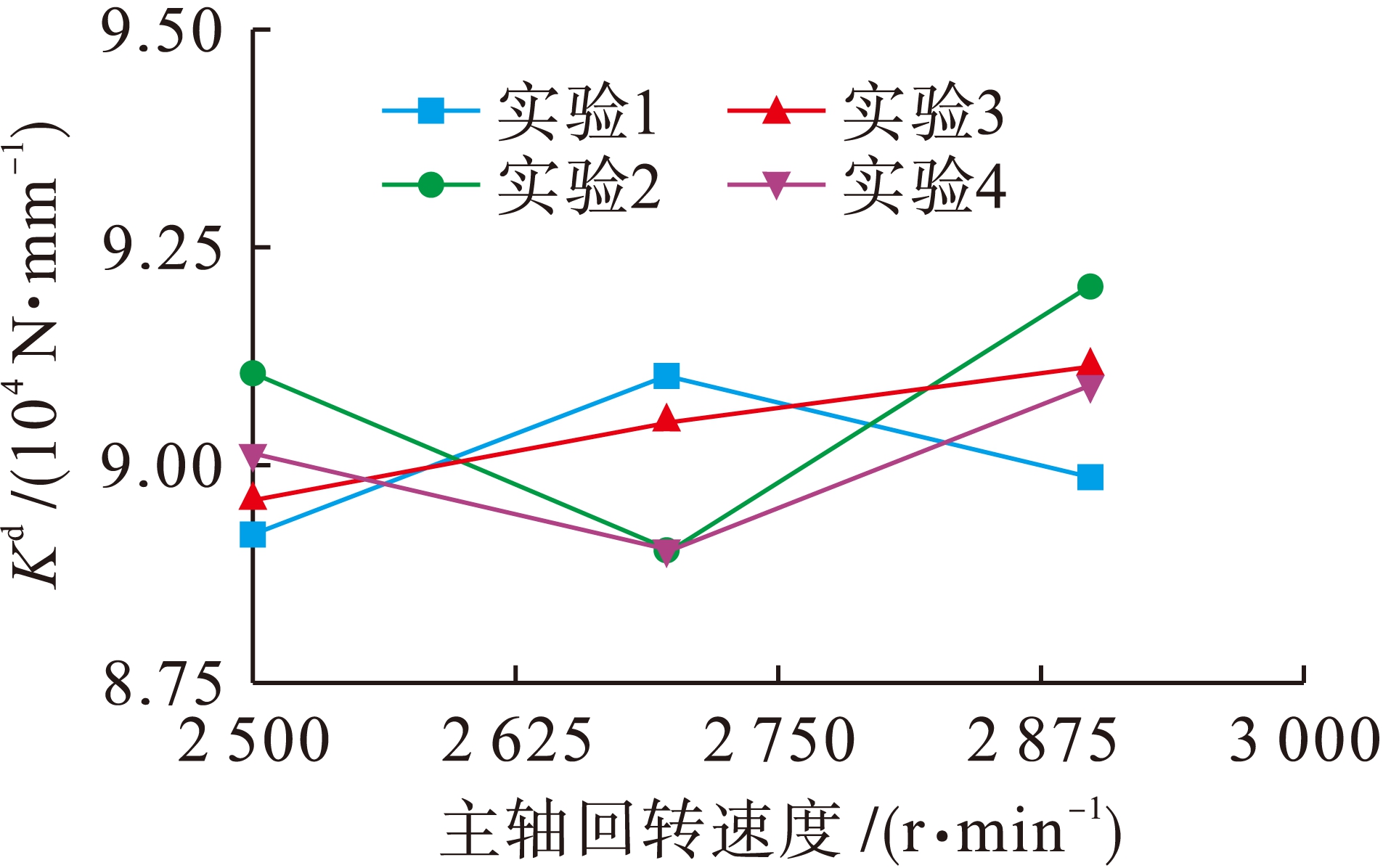
图12 淬硬钢耕犁力系数曲线
Fig.12 Plough force coefficient of hardened steel
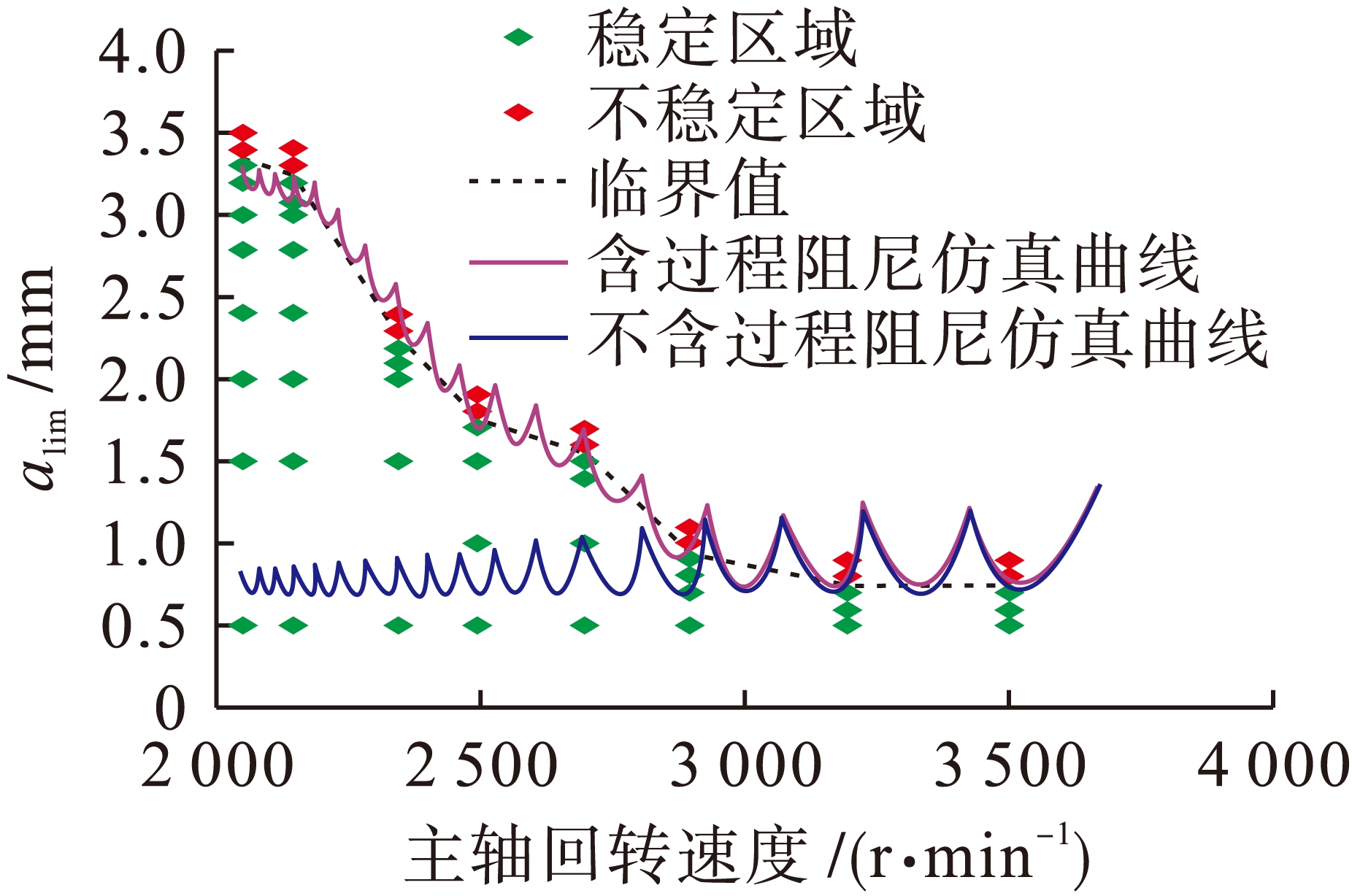
图13 仿真与实验数据对比曲线
Fig.13 Contrast curve for simulated and experimental data
通过以上分析,得出如下结论:
1) 本文建立了圆弧刃铣刀含有过程阻尼系数的动态铣削模型,提出了过程阻尼影响下的稳定叶瓣图的估算方法.通过实验测定圆弧刃铣刀稳定极限切深,带入数学模型中解算,得到过程阻尼系数,用能量等效代替法计算获得淬硬钢耕犁力系数.当已知某种材料的耕犁力系数时,可以预测不同刀具几何形状和切削条件下的过程阻尼系数和极限切深,预测出的过程阻尼系数可用于稳定叶瓣图的估算.
2) 在实验中可以看出,圆弧刃铣刀后角对端铣中的过程阻尼有显著影响.切削同一材料时,后角增大,过程阻尼系数增大,稳定极限切深增大,稳定区域增加,仿真结果与实验图像趋势一致.
3) 刃口半径改变对端铣中的过程阻尼同样有显著影响.切削同一材料时,刃口半径增大,过程阻尼系数增大,稳定极限切深增大,稳定区域增加,仿真结果与实验图像趋势一致.
参考文献(References):
[1]张为,程晓亮,郑敏利,等.切削加工表面完整性建模现状与发展趋势 [J].沈阳工业大学学报,2014,36(5):519-525.
(ZHANG Wei,CHENG Xiao-liang,ZHENG Min-li,et al.Status and development trend of surface integrity mo-deling in metal cutting [J].Journal of Shenyang University of Technology,2014,36(5):519-525.)
[2]张为,程晓亮,郑敏利,等.球头刀高速铣削模具钢热力分布 3D模拟 [J].沈阳工业大学学报,2015,37(2):171-175.
(ZHANG Wei,CHENG Xiao-liang,ZHENG Min-li,et al.3D simulation of thermal-force distribution in high-speedball end milling die steel [J].Journal of Shenyang University of Technology,2015,37(2):171-175.)
[3]Sisson T R,Kegg R L.An explanation of low-speed chatter effects [J].ASME Journal of Engineering for Industry,1999,91(4):951-958.
[4]Tlusty J.Analysis of the state of research in cutting dynamics [J].CIRP Annals-manufacturing Technology,1998,27(2):583-589.
[5]Tlusty J,Ismail F.Special aspects of chatter in milling [J].ASME Journal of Vibration,Acoustics,Stress,and Reliability in Design,1983,105(1):24-32.
[6]Minis I,Yanushevsky R,Tembo A,et al.Analysis of linear and nonlinear chatter in milling [J].CIRP Annals-manufacturing Technology,1990,39:459-462.
[7]Altintas Y,Budak E.Analytical prediction of stability lobes in milling [J].CIRP Annals-manufacturing Technology,1995,44(1):357-362.
[8]Budak E.Analytical models for high performance milling-part II:process dynamics and stability [J].International Journal of Machine Tools and Manufacture,2006,46:1489-1499.
[9]Altintas Y,Weck M.Chatter stability in metal cutting and grinding [J].CIRP Annals-manufacturing Technology,2004,53(2):619-642.
[10]Lee B Y,Tarng Y S,Ma S C.Modeling of the process damping force in chatter vibration [J].International Journal of Machine Tools and Manufacture,1995,35(7):951-962.
[11]Altintas Y,Eynian M,Onozuka H.Identification of dynamic cutting force coefficients and chatter stability with process damping [J].CIRP Annals-manufacturing Technology,2008,57(1):371-374.
[12]Huang C Y,Wang J J J.Mechanistic modeling of process damping in peripheral milling [J].ASME Journal of Manufacturing Science and Engineering,2007,129(1):12-20.
[13]李欣,李亮,何宁.过程阻尼对铣削系统稳定性的影响 [J].振动与冲击,2014,33(9):16-20.
(LI Xin,LI Liang,HE Ning.Influence of process damping on a milling system's stability [J].Journal of Vibration and Shock,2014,33(9):16-20.)
[14]李忠群,董亚峰,夏磊.考虑过程阻尼的切削稳定性建模与仿真分析 [J].湖南工业大学学报,2014,28(6):23-26.
(LI Zhong-qun,DONG Ya-feng,XIA Lei.Modeling and simulation on cutting process stability considering damping [J].Journal of Hunan University of Technology,2014,28(6):23-26.)
[15]杜红,黄胜勇.钛合金Ti6Al4V铣削加工过程阻尼模型稳定性预报 [J].黑龙江科技大学学报,2014,24(6):608-611.
(DU Hong,HUANG Sheng-yong.Stability prediction on process damping model of milling of titanium alloy Ti6Al4V [J].Journal of Heilongjiang University of Science & Technology,2014,24(6):608-611.)
[16]宋清华,唐委.一种新的在高速铣削中识别稳定性极限图的分析实验方法 [J].国外金属加工,2005,26(3):32-37.
(SONG Qing-hua,TANG Wei.A new analytical-experimental method for the identification of stability lobes in high-speed milling [J].Foreign Metal Processing,2005,26(3):32-37.)
[17]刘强,李忠群.数控铣削加工过程仿真与优化 [M].北京:航空工业出版社,2011.
(LIU Qiang,LI Zhong-qun.Simulation and optimization of NC milling process [M].Beijing:Aviation Industry Press,2011.)
(责任编辑:景 勇 英文审校:尹淑英)
ZHENG Min-li, MA Hui, YANG Lin, CHEN Jin-guo, WU Di
(School of Mechanical and Power Engineering, Harbin University of Science & Technology, Harbin 150080, China)
Abstract:In order to study the process damping of circular edge milling cutters in dynamic milling, the integrated optimization for existing models was performed through analyzing the geometric and technological parameters for the tool structures, and the mathematical model for the dynamic milling of circular edge milling cutters with process damping was established. Based on the improved mathematical model, the indentation volume of flank face was calculated. A large amount of cutting stable limit experiments were conducted, and the limit cutting depth under high speed condition was obtained. Simultaneously, the process damping coefficient of milling modal equation was solved by Matlab and ANSYS. In addition, the plough force coefficient of hardened steel was identified in combination with the energy balance equations, and the limit cutting depth can be predicted. The simulated results show that the relief angle and edge radius of the tool have a significant effect on the damping process, and the predicted limit cutting depth agrees with the experimental result.
Key words:process damping; plough force coefficient; limit cutting depth; circular edge milling; energy balance method; dynamic milling; ANSYS simulation; milling stability region
收稿日期:2015-09-15.
基金项目:国家自然科学基金重点资助项目(51235003).
作者简介:郑敏利(1964-),男,黑龙江哈尔滨人,教授,博士生导师,主要从事航空发动机典型件切削工艺等方面的研究.
机械工程
doi:10.7688/j.issn.1000-1646.2016.01.09
中图分类号:TH 113
文献标志码:A
文章编号:1000-1646(2016)01-0049-08
*本文已于2015-12-07 16∶20在中国知网优先数字出版. 网络出版地址: http:∥www.cnki.net/kcms/detail/21.1189.T.20151207.1620.050.html