位移曲线和弯矩位移曲线，并针对两种梁的荷载位移曲线和弯矩位移曲线分析简支梁的不同破坏形式，求出两种梁的极限弯矩和受剪承载力，与按照现行混凝土结构设计规范计算的理论结果进行比较.试验结果表明，模拟结果与理论结果比较接近，且符合钢筋混凝土简支梁破坏的基本规律，采用的分析模型是正确的，对该结构采用有限元分析的方法是有效的.杨 璐， 石旭武
(沈阳工业大学 建筑与土木工程学院， 沈阳 110870)
摘 要：为了对钢筋混凝土适筋梁和钢筋混凝土超筋梁的破坏过程进行数值模拟，利用ABAQUS软件的后处理程序分别绘出两种梁的荷载位移曲线和弯矩位移曲线，并针对两种梁的荷载位移曲线和弯矩位移曲线分析简支梁的不同破坏形式，求出两种梁的极限弯矩和受剪承载力，与按照现行混凝土结构设计规范计算的理论结果进行比较.试验结果表明，模拟结果与理论结果比较接近，且符合钢筋混凝土简支梁破坏的基本规律，采用的分析模型是正确的，对该结构采用有限元分析的方法是有效的.
关 键 词：钢筋混凝土； 简支梁； 数值模拟； 受剪承载力； 极限弯矩； 适筋梁； 超筋梁； 有限元分析
随着计算机和有限元方法的发展，有限元方法已广泛应用于众多实际工程中并且已成为研究钢筋混凝土结构的一个重要技术手段.本文利用ABAQUS[1]对钢筋混凝土简支梁中的适筋梁和超筋梁进行从开始加载到最终破坏的全过程仿真分析，并与按照现行混凝土结构设计规范计算的理论结果进行对比，能更深刻地认识和了解两种配筋情况下简支梁的破坏形态和机理，这对深入研究钢筋混凝土结构的基本力学性能、设计方法、构造措施和施工方法等有一定的参考价值和实用价值.
1.1 简支梁模型
两种配筋方式的钢筋混凝土简支梁的模型尺寸、配筋分布及荷载布置如图1～3所示(单位：mm).
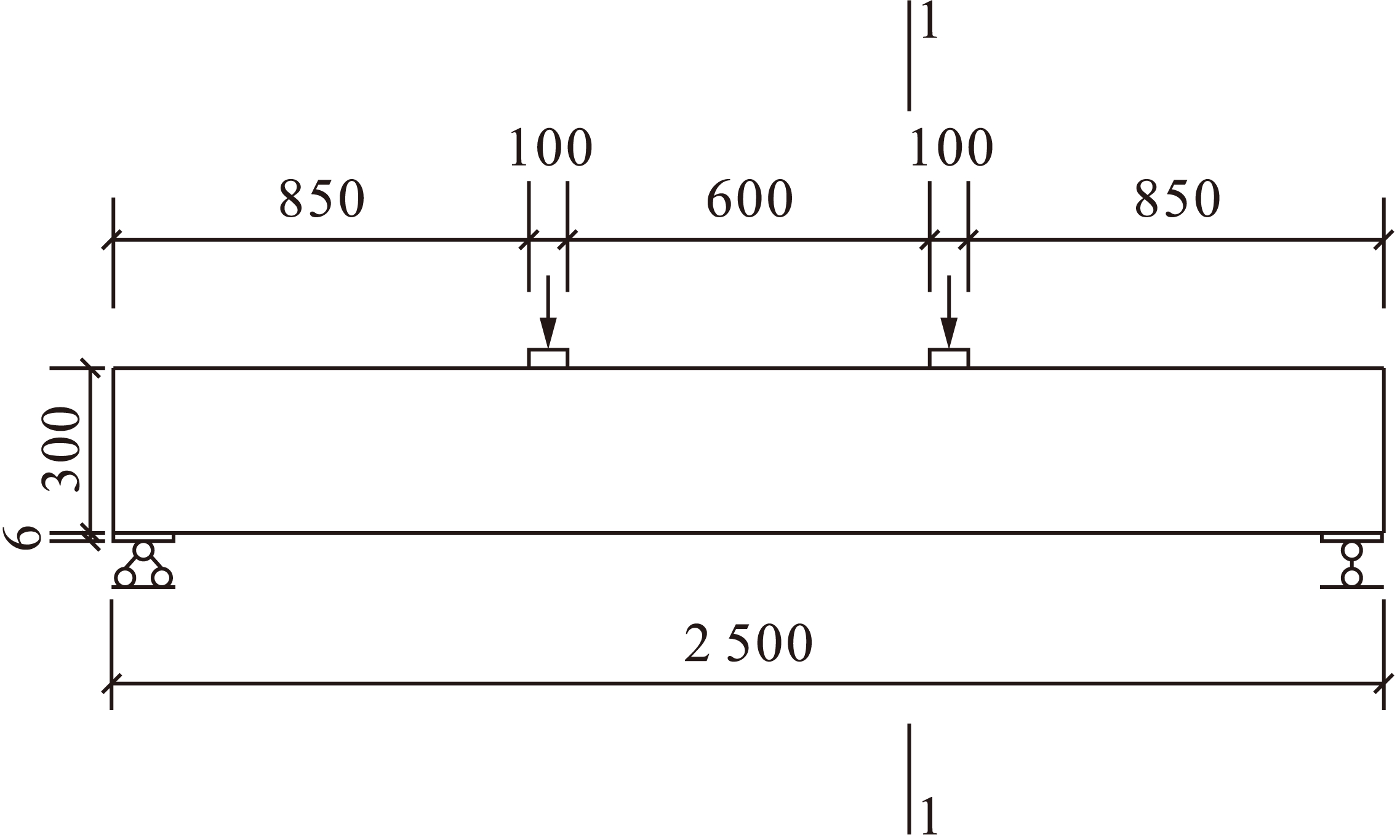
图1 梁尺寸及荷载布置
Fig.1 Beam size and load arrangement
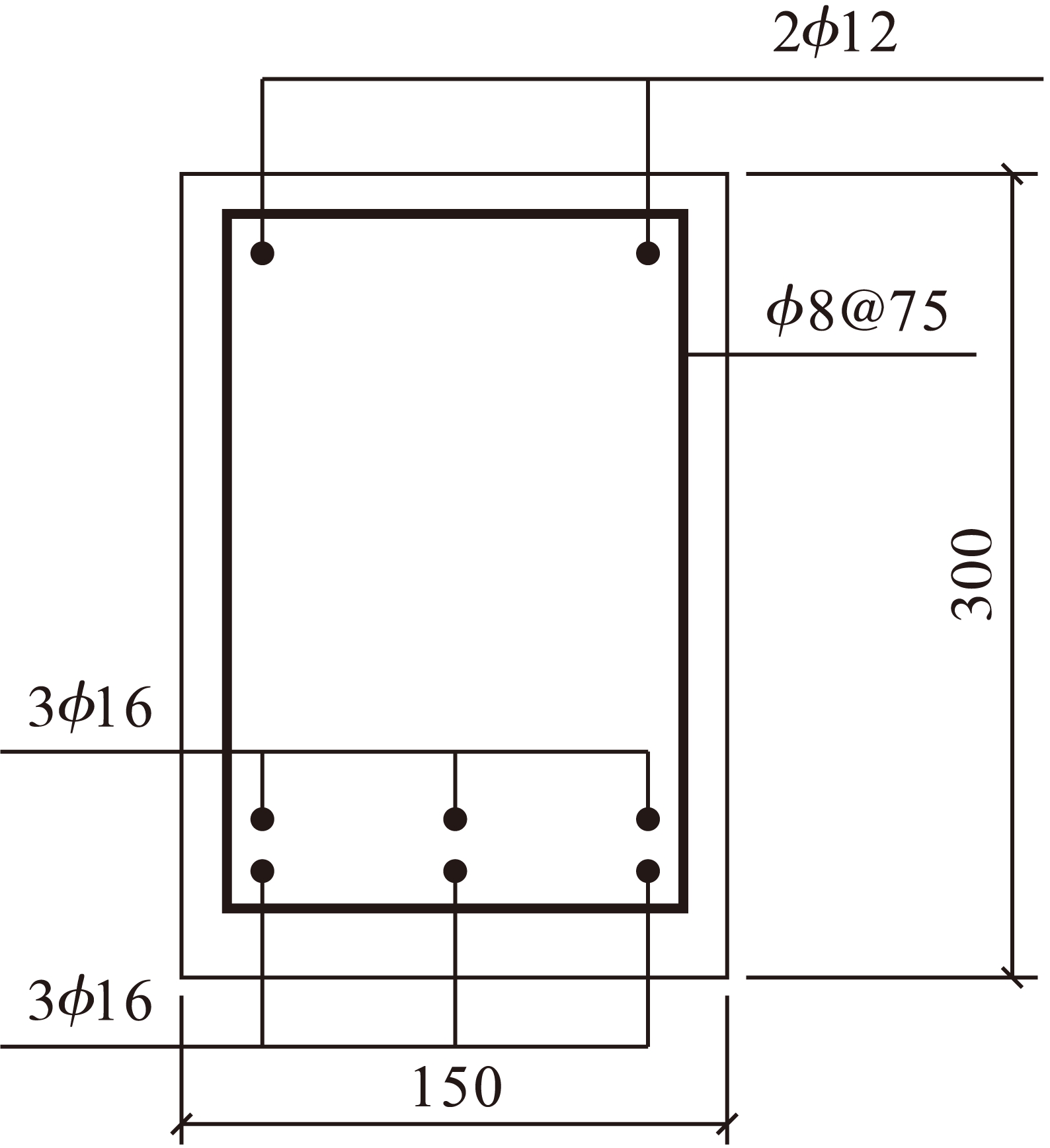
图2 梁-1配筋
Fig.2 Reinforcement of beam-1
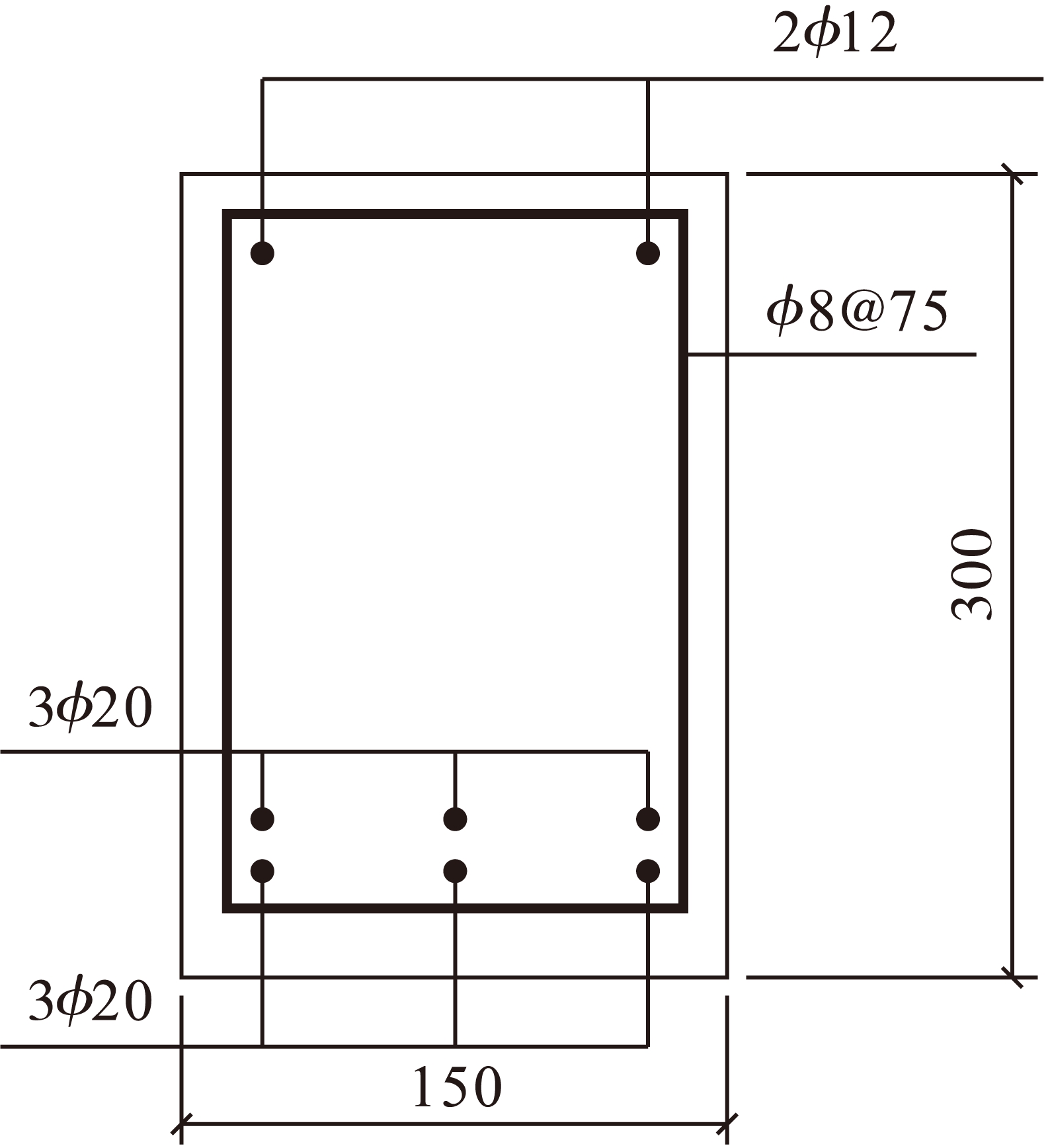
图3 梁-2配筋
Fig.3 Reinforcement of beam-2
1.2 单元类型选取及节点设置
混凝土为C3D8R单元；纵向钢筋和横向箍筋为T3D2单元.针对混凝土梁采用1 119个节点，900个单元；针对每个垫片采用1 819个节点，1 800个单元；针对钢筋骨架采用461个节点，429个单元.其中，节点具有水平和垂直位移两个自由度，节点间应力均为常量，通过embedded element接触关系将钢筋嵌入到混凝土单元中，以此来模拟钢筋与混凝土之间的粘结关系.
1.3 材料属性及定义
1.3.1 混凝土的材料属性
混凝土的本构采用Saenz和Sargin模型[2]，即
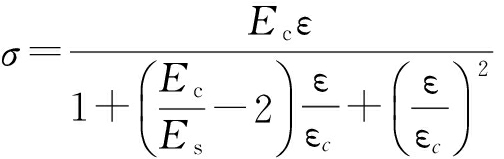
(1)
式中：ε为应变；Ec为变形模量；Es为弹性模量.取
εc=(1.028-0.108 
(2)
式中，fc为单轴抗压强度.
混凝土的基本材料参数如表1所示.
表1 混凝土的材料属性
Tab.1 Material properties of concrete
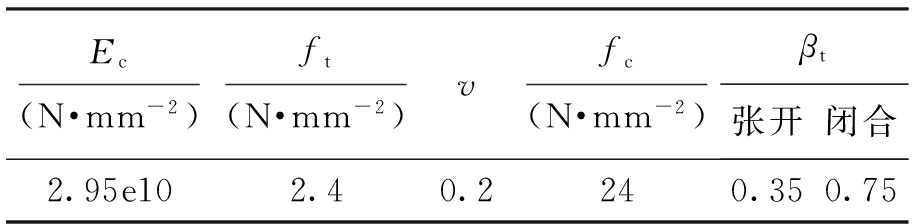
注：v为泊松比；ft为单轴抗拉强度；βt为裂缝间剪力传递系数.
1.3.2 钢材的材料特性
1) 本构关系.本文算例中，梁中纵向主筋、横向箍筋和钢支座垫板均采用理想弹塑性模型.
2) 屈服准则.钢材的屈服准则选用随动硬化双线性材料模型.钢材的基本材料参数如表2所示.
表2 钢材的材料属性
Tab.2 Material properties of steel
注：fy为钢材的屈服强度.
1.4 梁的承载计算
按照混凝土结构设计规范(GB 50010-2010)中的计算方法对梁-1、梁-2分别进行极限弯矩和抗剪承载力计算[3]，求梁-1的相对界限受压区高度ξb，即
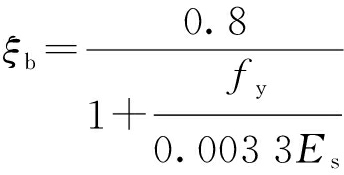
(3)
代入相关数据，经计算得相对界限受压区高度ξb=0.508，6φ16的面积As=1 206 mm2，则受压区高度为
(4)
式中：α为应力图形系数；b为梁截面高度.
根据式(4)并代入相关数据得受压区高度x=120.6 mm，梁截面的有效高度h0=300-(30-16/2+16+0.5×(30-16/2))=251 mm，经判断：x<ξbh0=0.508×251=127.5 mm，所以属于适筋梁.求极限弯矩，即
Mu=fyAs(h0-x/2)
(5)
根据式(5)并代入相关数据得极限弯矩，即Mu=65.79 kN·m，剪跨比
，取为3.
对于集中荷载作用下的矩形截面梁-1，抗剪承载力为
(6)
式中：fi为混凝土抗拉强度；fyv为钢筋抗拉强度；Asv为钢筋横截面面积；s为箍筋间距.
根据式(6)代入数据经计算得梁-1的抗剪承载力，即Vu=147.9 kN，对于梁-2，判断是否为适筋梁，6φ20的面积As=1 884 mm2.梁-2的实际配筋率和最大配筋率表达式分别为
(7)
(8)
将式(7)、(8)分别代入相关数据经计算得，ρ=0.05，ρb=0.033 8，经判断：ρ>ρb，所以属于超筋梁.h0=300-(30-18/2+18+0.5×(30-18/2))=250.5 mm.钢筋应力为
σs=0.003 3Es(0.8/ξ-1)
(9)
式中，ξ为相对受压区高度.由于
αfcbh0ξ=σsAs
(10)将式(9)代入式(10)得，1.0×24×150×250.5ξ=627×(0.8/ξ-1)×1 884，经计算得ξ=0.56>0.508，从而计算出极限弯矩为
Mu=σsAsh0(1-0.5ξ)
(11)
根据式(11)代入数据得Mu=99.1 
，取为3.
对于集中荷载作用下的矩形截面梁-2，抗剪承载力计算公式经代入相关数据计算得Vu=147.7 kN.
1.5 仿真模型的建立
为了提高数值分析的精度和降低误差，在数值模拟过程中对有限元网格划分和单元模型进行不断改进，通过对比分析，选择合适的单元网格划分和加载方式.
1.5.1 单元网格划分
在ABAQUS程序中采用sweep网格划分技术[4]，所有的单元网格均为正六面体[5].同时为了避免模型出现局部受压破坏，在加载点和支座处均加设6 mm厚的钢垫片.另外，为了避免出现应力集中，对加载点和支座处的网格划分进行了细化.仿真模型及单元如图4～6所示.
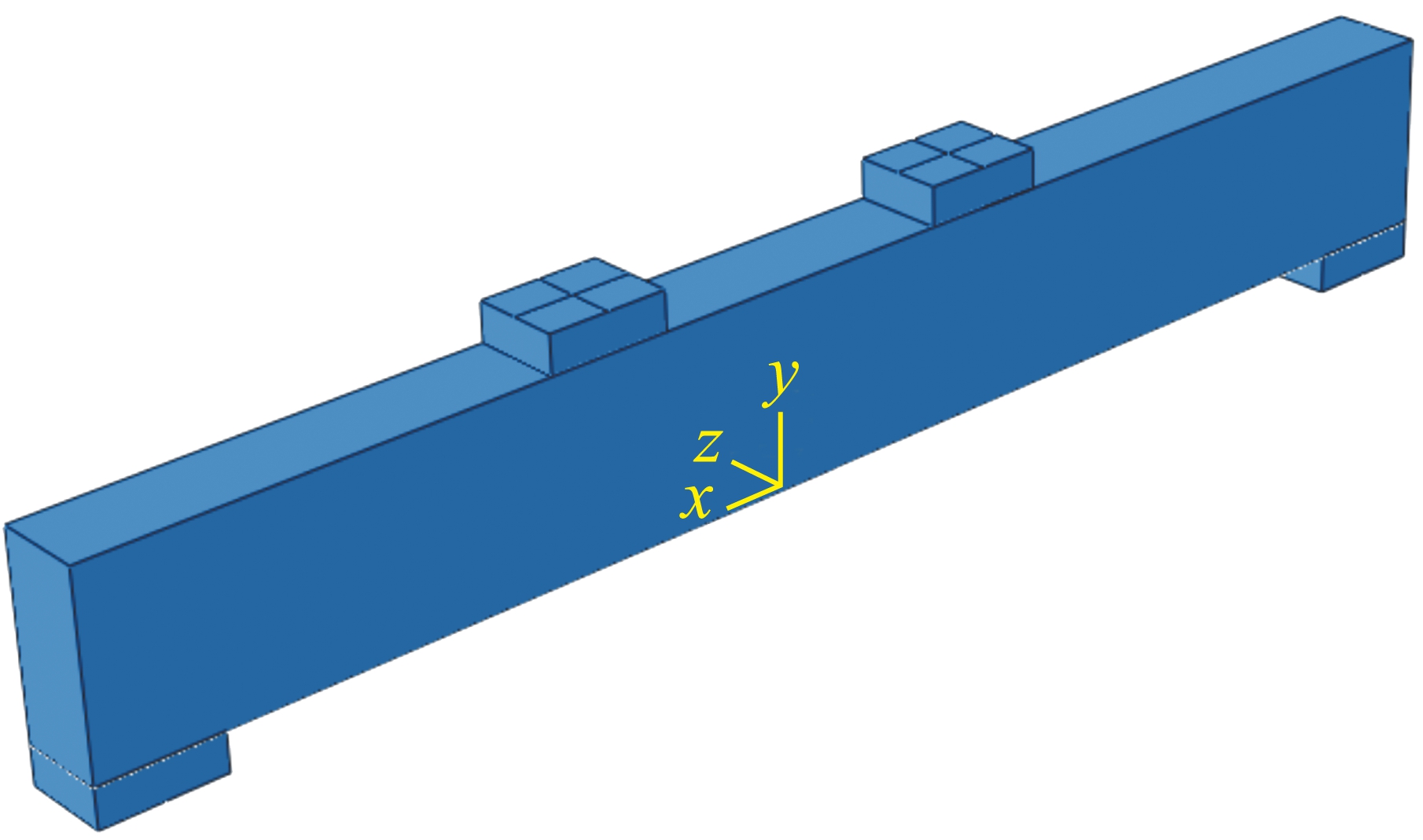
图4 梁的模型
Fig.4 Model for beam
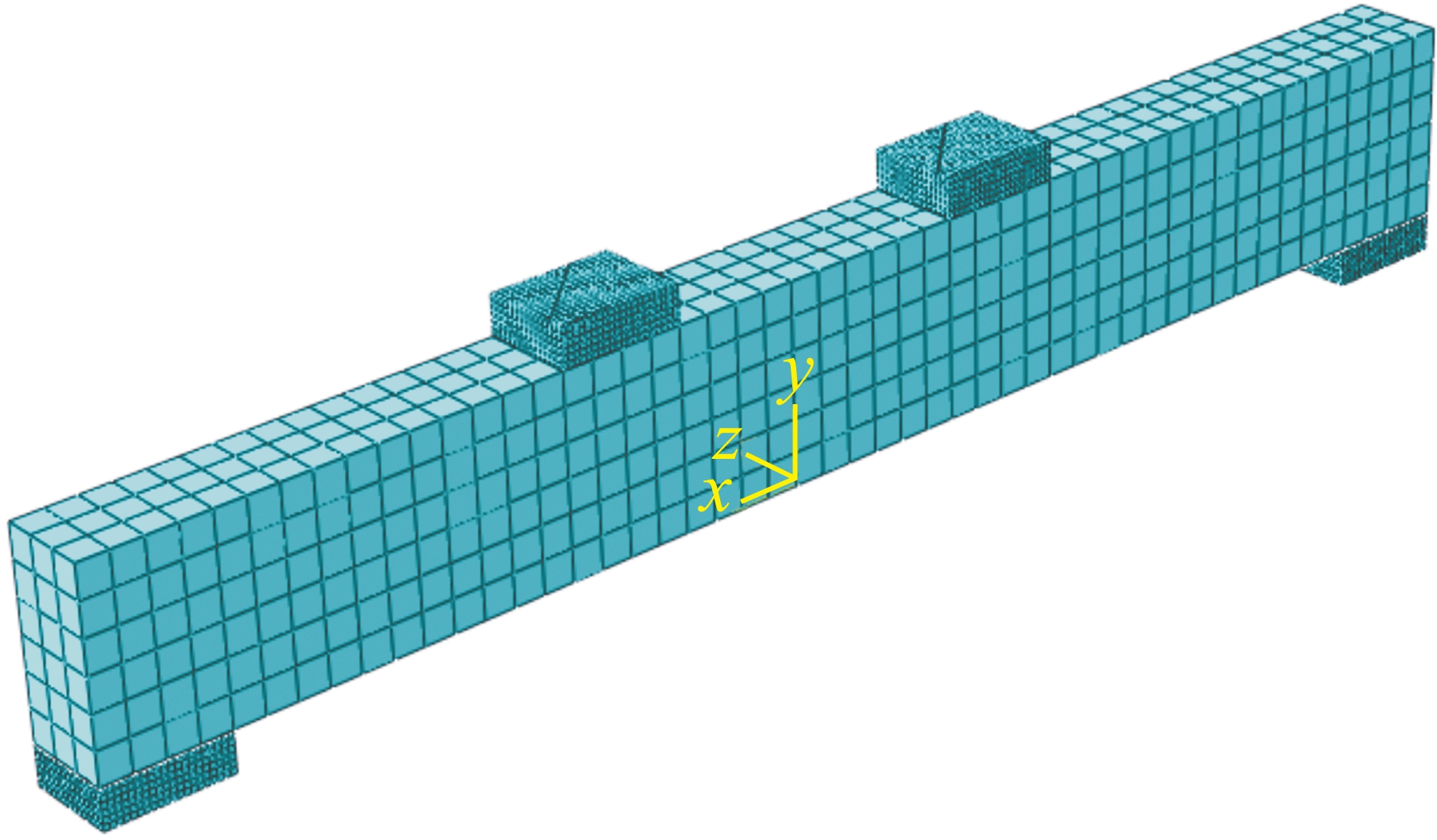
图5 单元网格
Fig.5 Element mesh
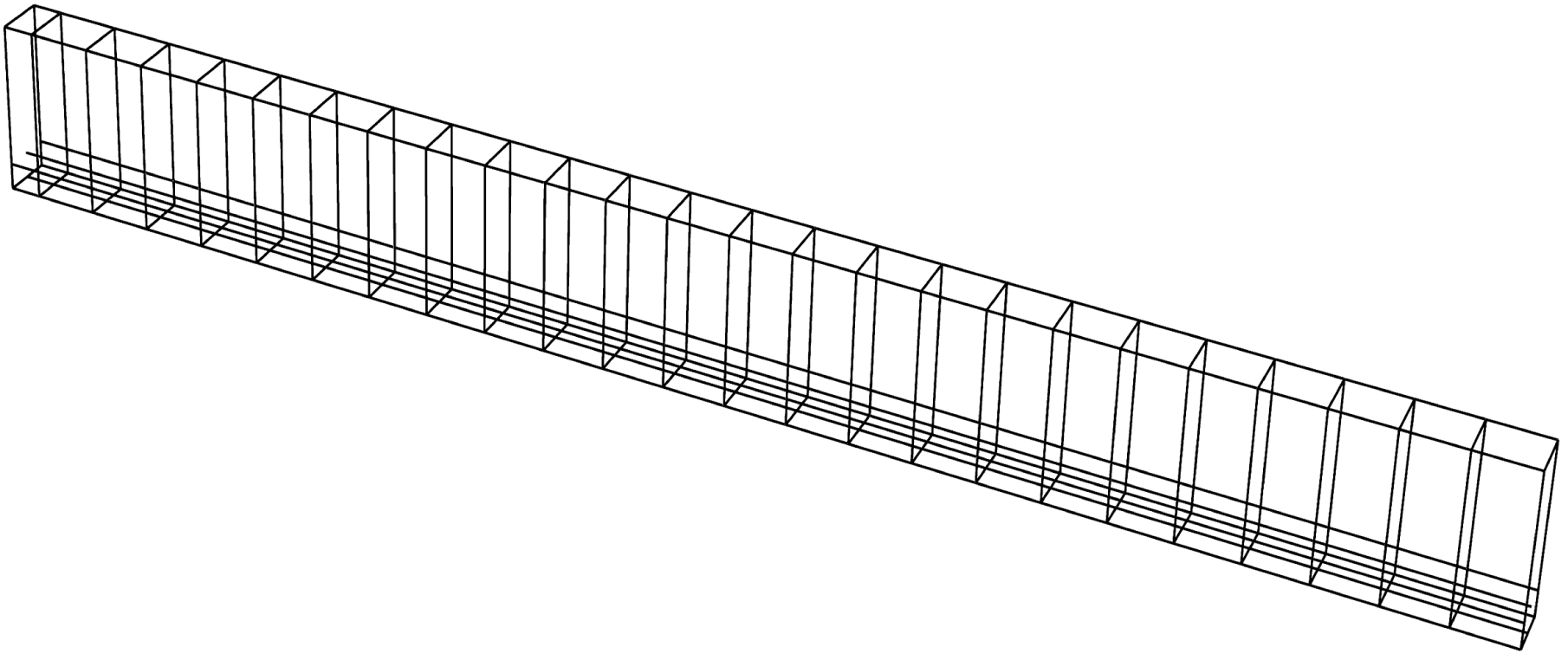
图6 钢筋单元
Fig.6 Rebar element
1.5.2 加载方式
本文中利用位移加载的方式进行加载，即调用Amplitudes建立加载规律，在加载点垫板中心施加一竖向位移，即UY=-1 mm.
1.6 分析步的设置及模型求解
将初始增量步设为0.2，最小增量步设为10-6，最大增量步设为500，最大增量步数目设为1 000.最终本文算例成功收敛.
图7、8分别为通过ABAQUS程序计算所得到的梁-1的荷载-跨中挠度关系曲线和跨中弯矩跨中挠度关系曲线.图9、10分别为通过ABAQUS程序计算所得到的梁-2的荷载跨中挠度关系曲线和跨中弯矩跨中挠度关系曲线.
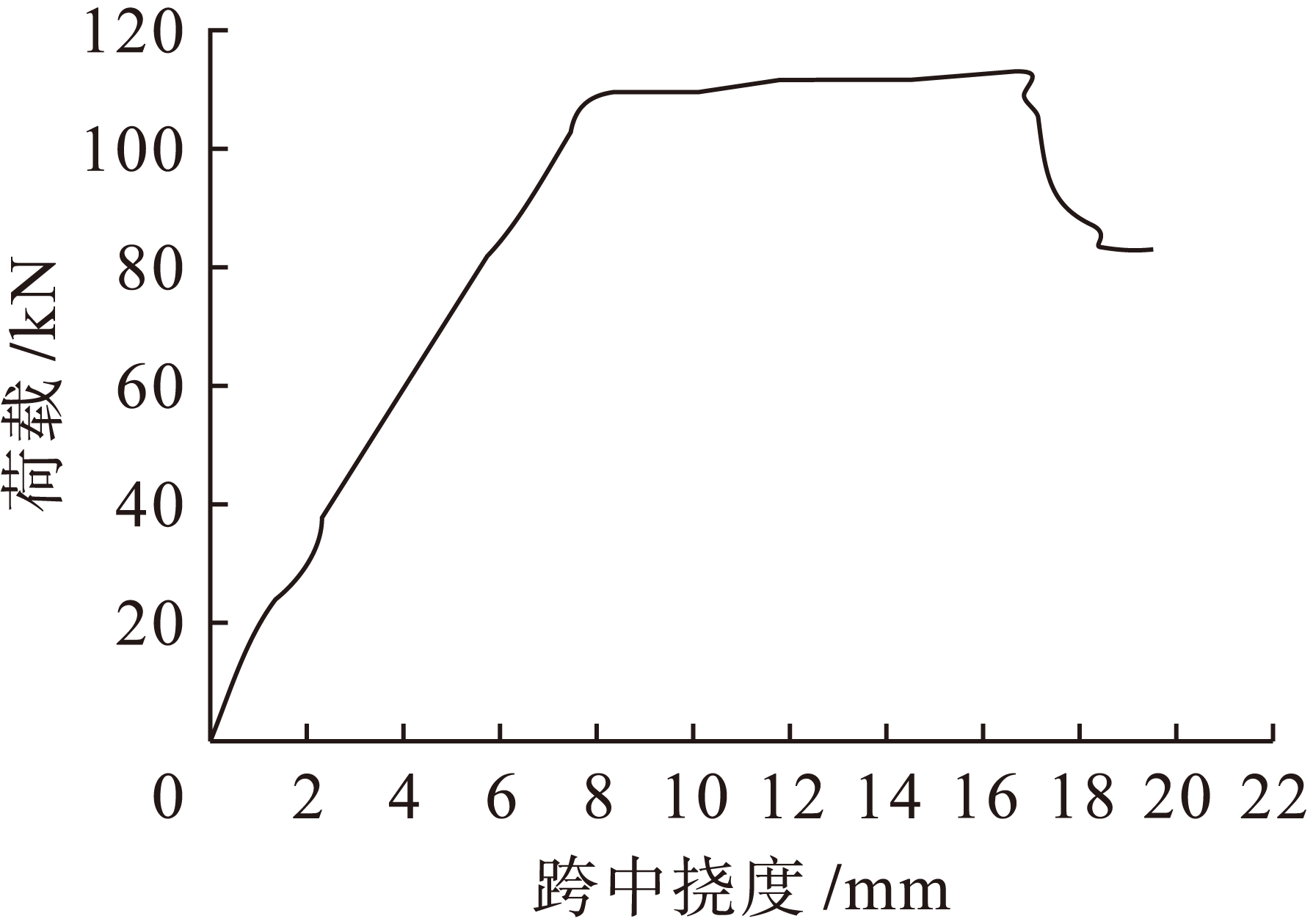
图7 梁-1的荷载跨中挠度关系曲线
Fig.7 Relationship between load and midspan deflection of beam-1
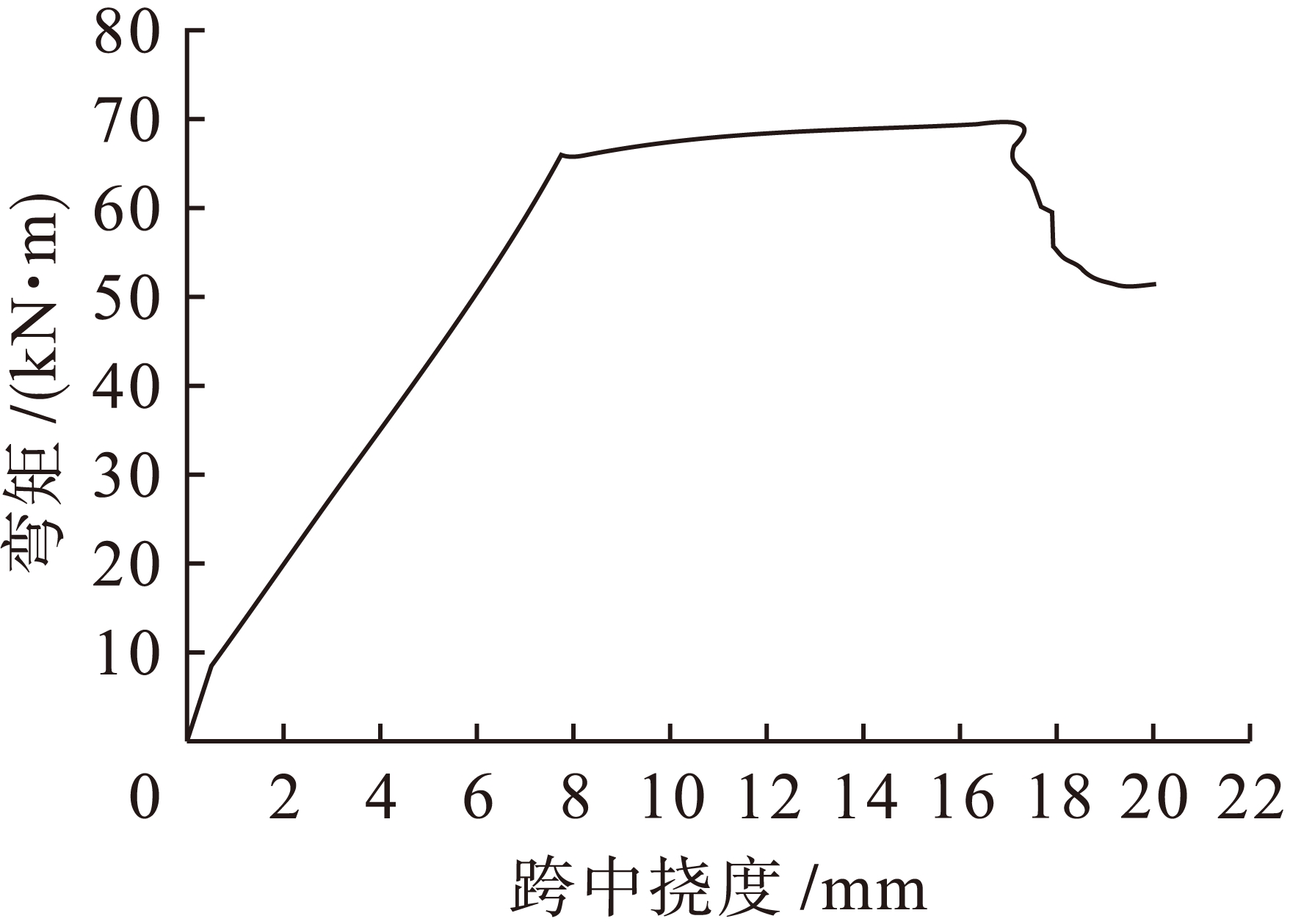
图8 梁-1的弯矩跨中挠度关系曲线
Fig.8 Relationship between bending moment and midspan deflection of beam-1
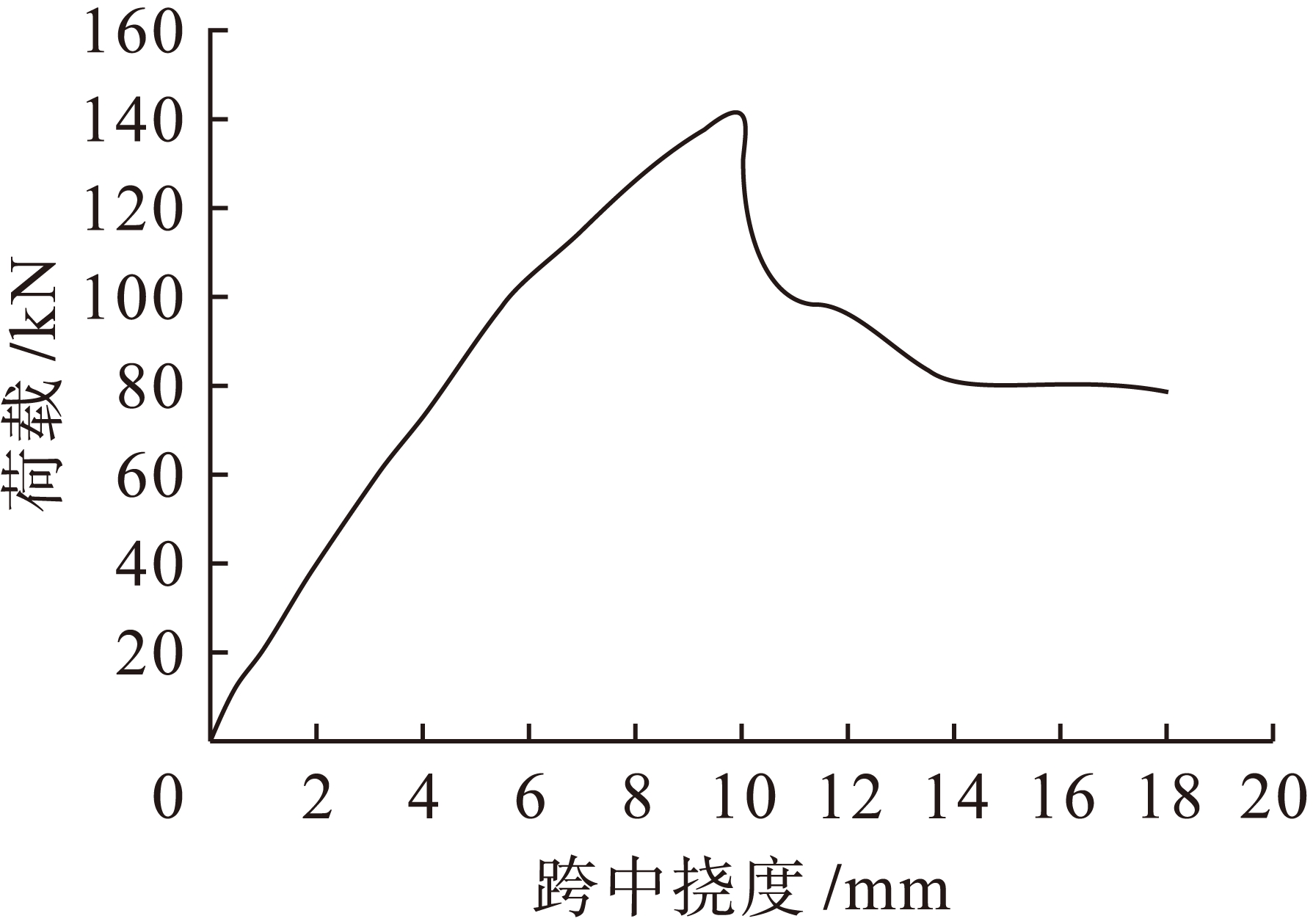
图9 梁-2的荷载跨中挠度关系曲线
Fig.9 Relationship between load and midspan deflection of beam-2
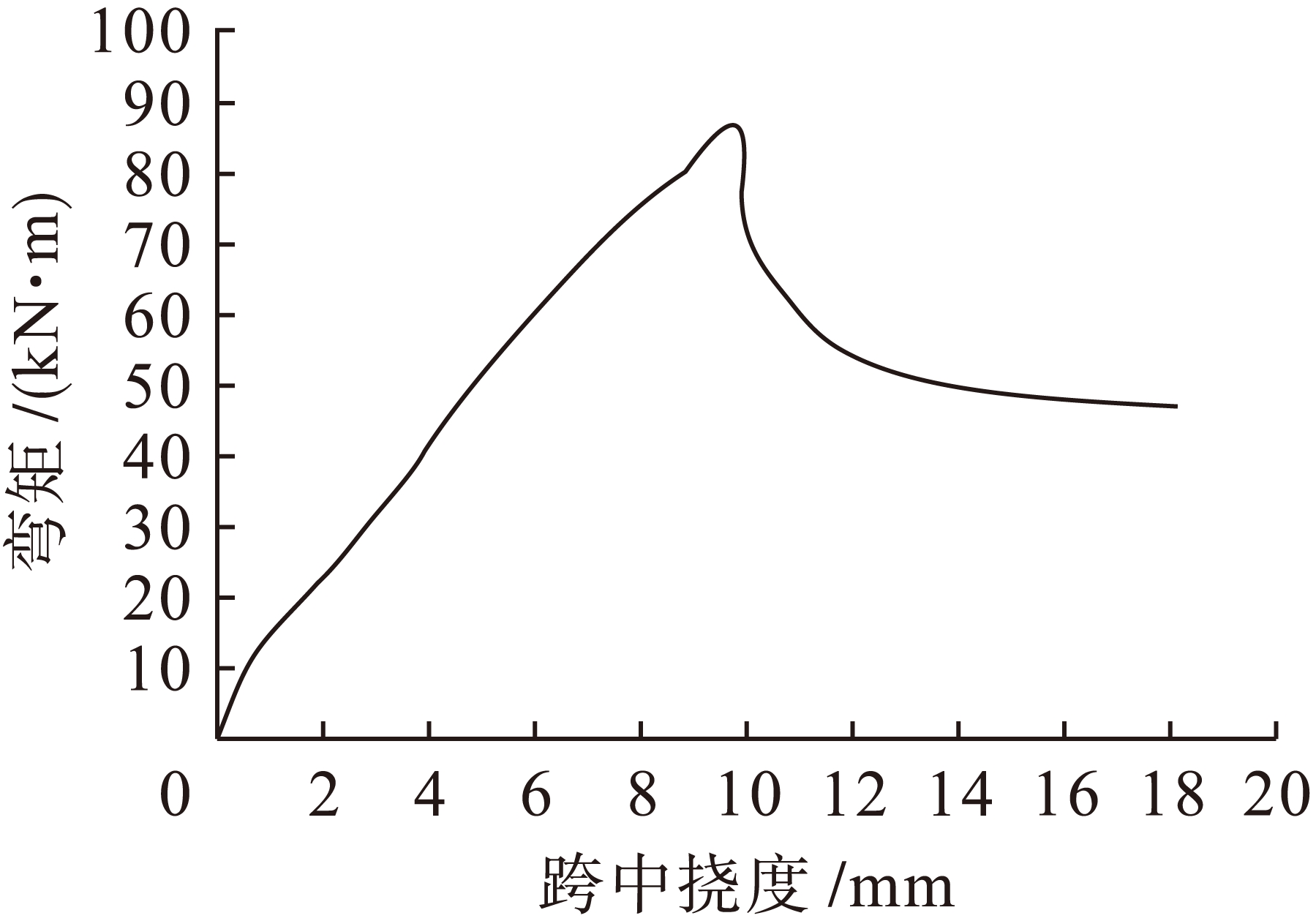
图10 梁-2的弯矩跨中挠度关系曲线
Fig.10 Relationship between bending moment and midspan deflection of beam-2
由图7、8可以得出，钢筋混凝土适筋梁剪切破坏[6]的受力基本特性能由梁-1的荷载跨中挠度的关系曲线形态和跨中弯矩跨中挠度的关系曲线形态大致表现出来，并且钢筋混凝土简支梁的弯剪破坏[7]形态和梁-1的荷载跨中挠度曲线形态非常符合.当简支梁-1的跨中截面的纵筋受拉并且屈服后，由于混凝土裂缝[8]的持续扩张，导致混凝土受压区高度不断减小，在外部施加的荷载基本保持不变的情形下，反而简支梁-1的受压区混凝土所受的剪应力和正应力还在持续递增，并且当受压区混凝土所受的剪应力达到混凝土强度极限状态时，简支梁-1就会发生剪切破坏，梁-1所能承受的外部荷载就会迅速降低.
由图9、10可以得出，超筋梁的试验[9]荷载跨中挠度曲线与梁-2的荷载跨中挠度关系曲线很类似，在梁-2的荷载达到极限状态下，并没有出现相对于梁-1那样所表现出的具有延时性的屈服平台[10]，反倒是没有预兆性的骤然跌落.由图7～10可以观察并计算出梁-2的极限弯矩值比梁-1的极限弯矩值增加约26%，而梁-2的受拉区配筋率比梁-1的受拉区配筋率增加约56%，二者对比发现受拉区配筋率增加量比极限弯矩值增加量多出约115%，结果表明，梁-2的受拉区相对于梁-1的受拉区所增加的纵向钢筋的抗拉强度对于梁的抗弯并没有完全发挥作用，其受力特点与超筋梁[11]的受力特点极其相似.
表3、4分别为适筋梁和超筋梁的规范理论计算结果与ABAQUS程序计算结果的比较.
表3 梁-1的理论值与模拟结果比较
Tab.3 Comparison between theoretical values and simulated results of beam-1
表4 梁-2的理论值与模拟结果比较
Tab.4 Comparison between theoretical values and simulated results of beam-2
结合表3、4可以得出，梁-1的ABAQUS程序计算的跨中最大弯矩值比按照规范GB 50010-2010计算的梁-1的极限弯矩值偏大，但二者较接近；梁-2的ABAQUS程序计算的跨中最大弯矩值比按照规范GB 50010-2010计算的梁-2的极限弯矩值低很多；梁-1和梁-2按照规范GB 50010-2010计算的梁的斜截面抗剪承载力均比ABAQUS程序计算的最大剪力值偏高，但是梁-2的ABAQUS程序计算的最大剪力值与按照规范GB 50010-2010计算的梁的斜截面抗剪承载力较接近.
通过ABAQUS程序成功实现了钢筋混凝土超筋梁和适筋梁的数值模拟破坏过程，并将按照混凝土结构设计规范GB 50010-2010计算的理论结果和ABAQUS的计算结果进行对比，可以得出对于超筋梁，ABAQUS计算的弯矩值和剪力值分别比按照混凝土结构设计规范GB 50010-2010计算的理论结果减小约12.5%和4.76%；对于适筋梁，ABAQUS计算的弯矩值比按照现行混凝土结构设计规范计算的理论结果增大约4.68%，而ABAQUS计算的剪力值比按照现行混凝土结构设计规范计算的理论结果减小约18.1%，但其误差均在可取范围内.经分析，误差产生原因总结如下：
1) ABAQUS程序计算的最大剪力并没有考虑纵向钢筋的销栓作用以及骨料的咬合力；
2) 虽然ABAQUS利用植入技术(embedded element)可以很好地解决钢筋与混凝土之间的粘结关系，但是其无法实现钢筋的滑移，这与实际情况有所偏差，导致梁的计算刚度比实际大很多；
3) 有限元分析方法是将计算模型简化为具有均匀性、各向同性等特点，而钢筋混凝土是一种非均质的、力学性能复杂且影响因素较多的弹塑性材料，很明显这种简化与实际结构性能本身存在明显差异会导致计算结果与实际有所出入，并且在ABAQUS程序的建模过程中，材料属性、模型各部分之间的接触、边界条件的设置、荷载的施加、网格划分的数量和精度以及分析步的设置等都会对ABAQUS程序的计算结果产生影响.
通过该算例的计算和比较，其结果表明，在ABAQUS程序中利用所建立的梁单元模型对钢筋混凝土简支梁破坏过程进行仿真模拟是行之有效的，为今后类似的结构仿真分析提供了借鉴.
参考文献(References)：
[1]王玉镯.ABAQUS结构工程分析 [M].北京：中国建筑工业出版社，2010.
(WANG Yu-zhuo.ABAQUS and structural engineering analysis [M].Beijing：China Architecture and Building Press，2010.)
[2]徐仲卿，袁泉，杨振坤，等.早龄期混凝土力学性能试验及其单轴本构模型 [J].沈阳工业大学学报，2015，37(1)：92-96.
(XU Zhong-qing，YUAN Quan，YANG Zhen-kun，et al.Mechanical property experiment and uniaxial constitutive model for concrete at early age [J].Journal of Shenyang University of Technology，2015，37(1)：92-96.)
[3]中华人民共和国建设部.GB 50010-2010混凝土结构设计规范 [S].北京：中国建筑工业出版社，2002.
(The Ministry of Construction of the People’s Republic of China.GB 50010-2010 Concrete structure design code [S].Beijing：China Architecture and Building Press，2002.)
[4]费康.ABAQUS 在岩土工程中的应用 [M].北京：中国水利水电出版社，2010.
(FEI Kang.ABAQUS application in geotechnical engineering [M].Beijing：China Water Conservancy and Hydropower Press，2010.)
[5]刘林林，屠永清，叶英华.基于ABAQUS的钢管混凝土L形柱有限元分析 [J].沈阳工业大学学报，2011，33(3)：349-354.
(LIU Lin-lin，TU Yong-qing，YE Ying-hua.Finite element analysis of L shaped concrete filled steel tubular column based on ABAQUS [J].Journal of Shenyang University of Technology，2011，33(3)：349-354.)
[6]程文瀼，颜德媛.混凝土结构设计原理 [M].北京：中国建筑工业出版社，2011.
(CHENG Wen-xiang，YAN De-yuan.Concrete structure design principle [M].Beijing：China Architecture and Building Press，2011.)
[7]沈新普，冯金龙，代树红，等.基于DSCM的混凝土结构变形局部化试验 [J].沈阳工业大学学报，2008，30(2)：212-218.
(SHEN Xin-pu，FENG Jin-long，DAI Shu-hong，et al.Experimental study on deformation localization of concrete structures with DSCM [J].Journal of Shenyang University of Technology，2008，30(2)：212-218.)
[8]沈新普，杨璐，混凝土损伤理论及试验 [M].北京：科学出版社，2009.
(SHEN Xin-pu，YANG Lu.The concrete damage theory and experiment [M].Beijing：Science Press，2009.)
[9]王丽，邓思华.基于ABAQUS的混凝土梁受弯破坏实验非线性分析 [J].土木建筑工程信息技术，2010，2(1)：64-67.
(WANG Li，DENG Si-hua.Based on ABAQUS nonlinear analysis of concrete beam bending damage experiment [J].Journal of Information Technology in Civil Engineering and Architecture，2010，2(1)：64-67.)
[10]彭建勋，詹润涛，梅保贤.钢筋混凝土简支梁破坏过程数值分析 [J].信阳师范学院学报(自然科学版)，2009，22(3)：471-474.
(PENG Jian-xun，ZHAN Run-tao，MEI Bao-xian.The reinforced concrete beam failure process of numerical analysis [J].Journal of Xinyang Normal University(Natural Science Edition)，2009，22(3)：471-474.)
[11]王铁成.混凝土结构 [M].北京：中国建筑工业出版社，2005.
(WANG Tie-cheng.Concrete structure [M].Beijing：China Architecture and Building Press，2005.)
(责任编辑：钟 媛 英文审校：尹淑英)
YANG Lu, SHI Xu-wu
(School of Architecture and Civil Engineering, Shenyang University of Technology, Shenyang 110870, China)
Abstract：In order to perform the numerical simulation for the failure process of both balanced-reinforced beam and over-reinforced beam of reinforced concrete, the load-displacement curve and bending moment-displacement curve were drawn with the postprocessor of software ABAQUS. Aiming at the load-displacement curve and bending moment-displacement curve, the different failure types of simply supported beam were analyzed. In addition, the ultimate bending moment and shear capacity of two beams were obtained, and were compared with the results calculated according to the current concrete structure design specifications. The results show that the simulated results are close to the theoretical results, and are consistent with the basic damage law for the simply supported beam of reinforced concrete. The adopted analysis model is correct, and the finite element analysis method is effective for the present structure.
Key words：reinforced concrete; simply supported beam; numerical simulation; shear capacity; ultimate bending moment; balanced-reinforced beam; over-reinforced beam; finite element analysis
收稿日期：2015-06-24.
基金项目：国家自然科学基金资助项目(111021181).
作者简介：杨 璐(1973-)，女，山东掖县人，教授，博士，主要从事混凝土弹塑性损伤本构和ABAQUS数值模拟等方面的研究.
doi：10.7688/j.issn.1000-1646.2016.01.17
中图分类号：TU 375.1
文献标志码：A
文章编号：1000-1646(2016)01-0097-05
*本文已于2015-12-07 16∶16在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20151207.1616.002.html