李 勇， 施艳春
(沈阳工业大学 电气工程学院， 沈阳 110870)
摘 要：为了提高风电场风速预测的准确性，将不同预测方法的权重推广到权重序列，生成权重矩阵，同时采用新的预测误差更新权重矩阵，获得所需模型.建立三种单一预测模型，统计它们十天的预测误差，获得误差序列，在此基础上，提出动态熵权法.采用熵权法确定各单一预测模型在96个预测时刻的权值，并根据新的24小时预测误差更新误差序列和权重矩阵，从而获得动态组合预测模型.结果表明，动态组合预测模型的整体误差指标比单一预测模型较小，预测精度显然增高，证明了所建模型有效且实用.
关 键 词：风速预测； 神经网络； 时间序列； 数值天气预报； 熵权； 组合预测； 动态组合预测
风力发电机的随机性、波动性以及逆负荷特性等不利特征冲击着电网的安全可靠运行，如何能够获得精准的风速预测数据对于保证电网安全以及更有效利用风力发电具有重要的意义 [1].当前风速预测的主流方法有物理方式、统计方式及组合预测方式等 [2-3]，在预测效果上各有优缺点.统计方式在风电场历史数据的基础上建立相应模型进行预测；物理方式采用数值天气预报(Numerical weather prediction，NWP) [4]；组合预测 [5-7]结合不同预测方法优点，预测精度高.常用组合模型的权重不能及时随模型误差进行调整，影响模型预测结果，如文献[8]中的组合方法是对整个单一模型权重的直接确定且不变，当数据变化时不能及时调整权重.
本文对风电场风速进行短期预测，提出了一种基于动态熵权的组合预测模型，简称DGP.风电场风速数据具有按时间排序、离散和非线性的特点，根据风速历史数据建立差分自回归滑动平均模型(ARIMA)和神经网络(BP)两种数学模型对风速进行24 h预测(15 min采样间隔，96个时间点)，根据NWP预测模型获得24 h风速预测数据，与实际值对比，得到三种预测方式在每个时刻预测误差，滚动预测十天，获得三种方式在每个时刻的预测误差序列.根据预测误差序列，采用熵权法求得三种预测方式在每个时刻的权重序列，组合预测24 h风速值，并与实际值对比获得预测误差累加到预测误差序列中，更新权重序列，对下一个24 h风速进行预测，进而建立动态组合预测模型.
1.1 时间序列模型
时间序列ARIMA是基于自回归滑动平均模型提出来的 [9]，建模过程如下：风电场中缺测、丢失及不合理的数据采用插值或邻近数据进行替补或交换，然后对数据进行一阶差分，平稳性由单位根检验判断，最后采用AIC原则进行定阶 [10]，最小二乘法对参数进行估计，标准为误差的平方值最小，同时检验残差是否为白噪声.
1.2 BP神经网络模型
使用单隐层BP神经网络模型对未来风速进行预测，输入输出均为历史风速数据时间序列，通过训练数据训练BP神经网络对风速拟合并预测.最终选择隐层神经元数量为150，因为当100个隐层神经元时，拟合预测效果较差，150和200个时拟合预测效果精确，但选用200个神经元时训练时间过长，达到10 min左右，为减少预测时间，选用150个神经元.在网络训练中，tansig作为隐含层神经元传递函数 [11]，logsig作为输出层神经元传递函数，其他参数分别为：学习率0.05，训练要求精度0.000 01，训练最大次数1 000.
模型训练分别采用一个、三个和四个月的数据建立神经网络模型预测一天的风速，结果采用三个月数据建立的模型预测精度高，训练时间短，过多的数据不容易采集且模型训练时间较长，最终采用三个月的数据建立模型.
1.3 NWP风速预测模型
NWP是指在一定实际大气情况下，通过表示天气演变原委的热力学以及流体力学方程组进行求解来预报天气的情况 [12].经气象部门计算，得到的结果是一个大尺度的高空风速数据，通过风速切变特性公式计算折合到单台风机轮毂高度处的NWP风速预测值.
2.1 预测误差分析
对风电场风速分别建立ARIMA、BP和NWP预测模型，并进行24小时周期的动态循环预测，统计三种预测模型为期十天的误差序列.风速预测常用误差指标有均方根误差(RMSE)和平均相对误差(MRE)，用公式表示为
(1)
(2)
式中
为风速预测值；
v
t
为风速实测值；
N为预测值个数.本文采用RMSE对预测精度进行对比，为了方便观察误差规律，将预测时间分成四个时间段进行统计，结果如表1所示.
表1 预测误差统计
Tab.1 Prediction error statistics m/s
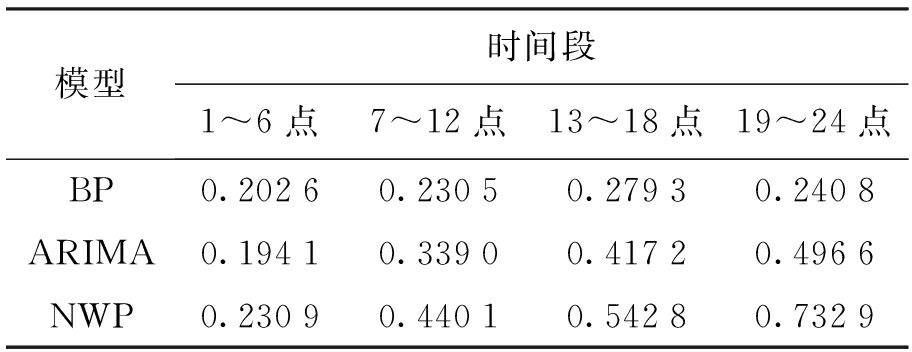
ARIMA对1～6点的超短期风速预测精度较高，随着预测时间增加，预测误差越来越大；BP整体的预测精度优于ARIMA和NWP，但并非一直如此，预测时间短的情况下，ARIMA误差小于BP，随着时间增长，神经网络的优越性越加显示出来；NWP的预测精度也是随着时间的增加而降低.
2.2 动态组合预测模型
在不同时间段，不同预测方法有着不同的表现，为此提出动态组合预测模型进行风速预测.建立DGP模型的关键是计算各模型的权重，本文提出了一种动态确定各预测方式在每个时刻权重系数的方法，得到每种预测方式的权重系数矩阵，各预测方式在每个时刻的权重由其在此时的预测误差所决定.
对信息理论中的信息熵进行改进，建立风电场风速动态组合预测模型，熵的概念来源于热力学，目前用于确定权重的文献有很多 [13-14].传统组合预测方法由熵权法确定单一模型权值，首先获得各单一模型的误差绝对值，记为 B=[ b ij ] m× n ， m=96， n=3，对其标准化处理得到 R=[ r ij ] m× n ，其中
(3)
由 R求得单一模型在各时刻误差占比为
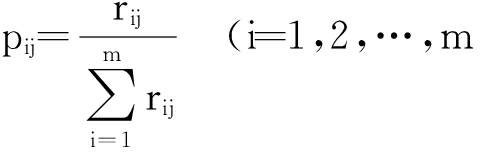；j=1，2，…，n)
(4)
单一模型熵值和权值分别表示为
p
ij (j=1，2，3)
(5)
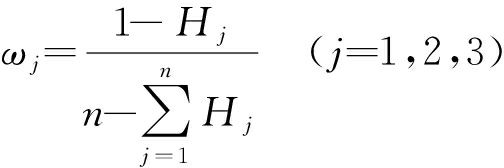
(6)
组合预测结果为 P= ω 1 P 1+ ω 2 P 2+ ω 3 P 3，式中， P 1， P 2， P 3为各单一模型的预测值.
动态组合预测的基本原理：对于 t预测时刻的目标序列{ x dt ， d=1，2，…，10； t=1，2，…，96}(连续十天在此时刻的实际值)，单项预测方法存在3种，设第 i种单项预测方法在第 d天 t时刻的预测值为{ x idt ， t=1，2，…，96； i=1，2，3； d=1，2，…，10}，并定义相对误差为
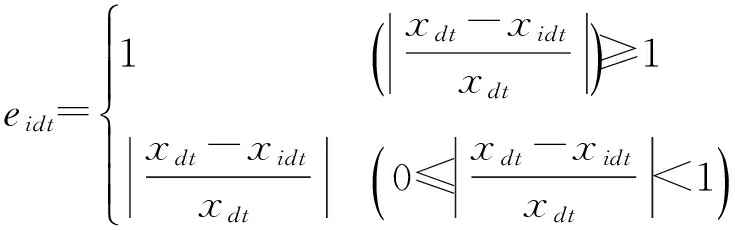
(7)
据此求得24小时96个时刻三种预测方式的相对误差序列.根据统计学理论，各预测方式的差异由偏差大的指标反映，在计算权重时保证熵值越大的属性最终的权重越小.
动态组合预测步骤如下：
1) 将各种单项预测方法的24小时96个时刻为期十天的动态预测误差取绝对值；
2) 在第1时刻，对三种预测方式十天的误差序列{ e i1 d }( d=1，2，…，10)进行归一化处理，即
；
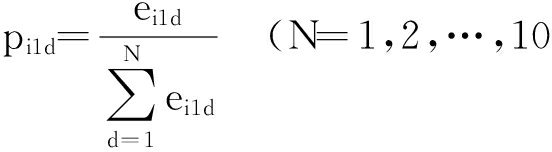(8)
3) 计算第 i种单项预测方法在第1时刻的相对误差熵值，即
p
id (i=1，2，3)
(9)
4) 计算第 i种单项预测方法在第1时刻变异程度系数，即
d i1 =1- h i1 ( i=1，2，3)
(10)
5) 计算各种预测方法在第1时刻的加权系数，即
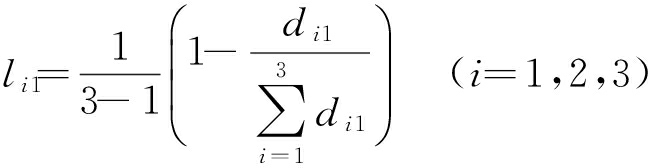
(11)
6) 返回步骤2)，计算各种预测方法在每个时刻的权重系数，最终获得的是一个3行96列的权重系数矩阵 W，即
(12)
7) 权重系数矩阵中的3行系数代表三种预测方法在每个时刻的权重系数，分别乘以各个预测方法在每个时刻的预测值并进行相加，最终获得预测结果，即 y j = l 1， j y 1， j + l 2， j y 2， j + l 3， j y 3， j ( j=1，2，…，96)
(13)
Y=[ y 1，…， y j ，…， y 96]
(14)
式中： y j 为第 j时刻组合预测值； Y为最终的24小时组合预测结果.
在风电场每隔24 h即可获得一组风速实际值，进而可获得三种预测方式的24 h预测误差，把最新预测误差统计到确定熵权的误差序列中，重新计算权重系数，这样每隔24 h就可根据实际预测误差更新权重，实现动态组合预测.
在我国东北某风电场建立测风塔，测风塔的高度为70 m，分别在70 m及以下每隔20 m的高度装设风速仪，风速测量起止时间：2013年12月3日—2014年12月4日，以风电场三个月50 m高度的风速数据作为训练数据，2014年3月5日的实际值作为检测数据.
运用ARIMA、NWP、固定权重的组合预测模型(简称GP)、BP以及随预测误差更新权重的DGP模型对上述风电场的风速进行预测，结果分别见图1与图2.
上述5种模型预测结果分别为RMSE NWP=0.486 7 m/s>RMSE ARIMA=0.361 7 m/s>RMSE BP=0.238 3 m/s>RMSE GP=0.194 1 m/s>RMSE DGP=0.187 9 m/s，MRE NWP=0.063 1>MRE ARIMA=0.041 1>
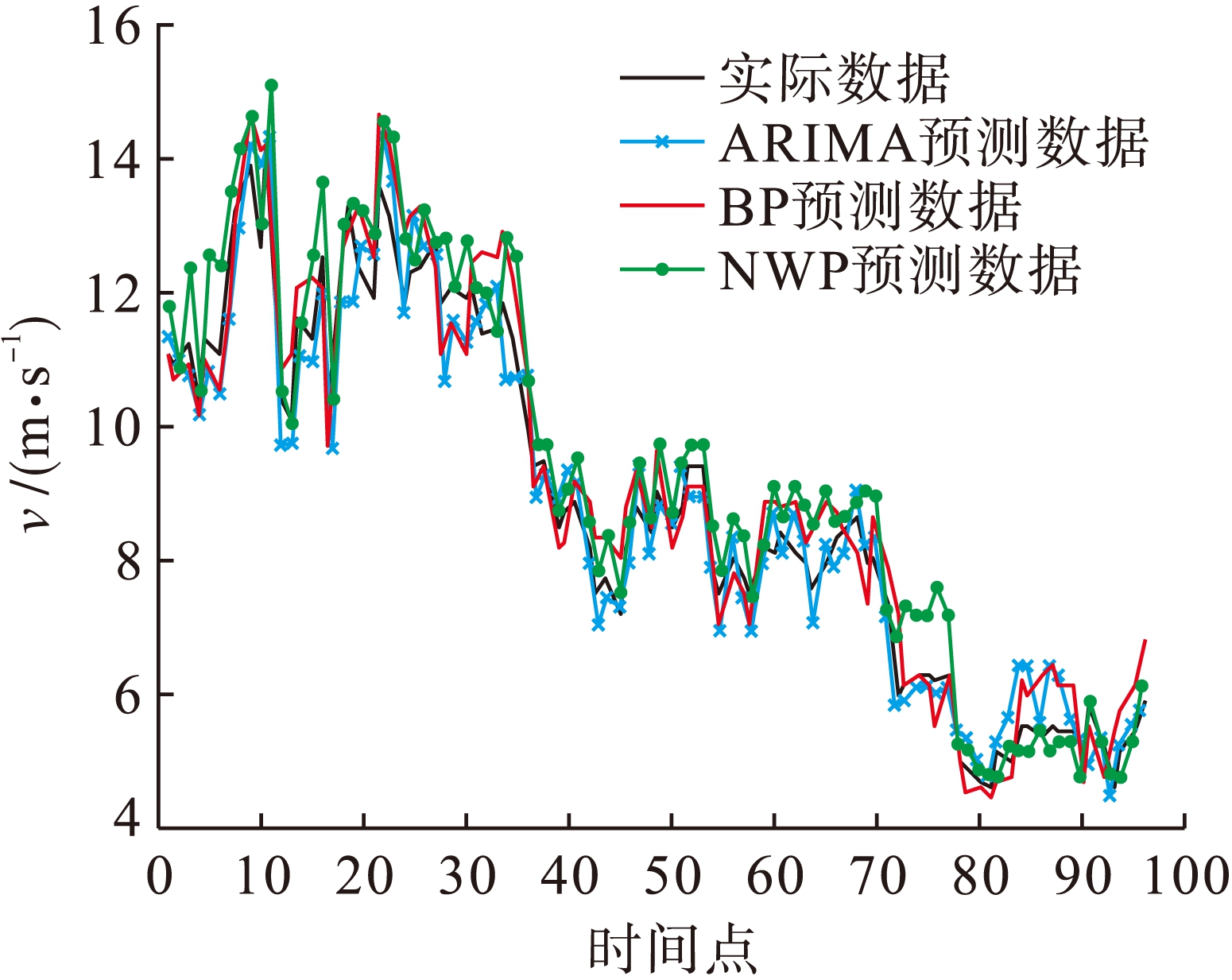
图1 单一模型预测结果
Fig.1 Forecast results of single model
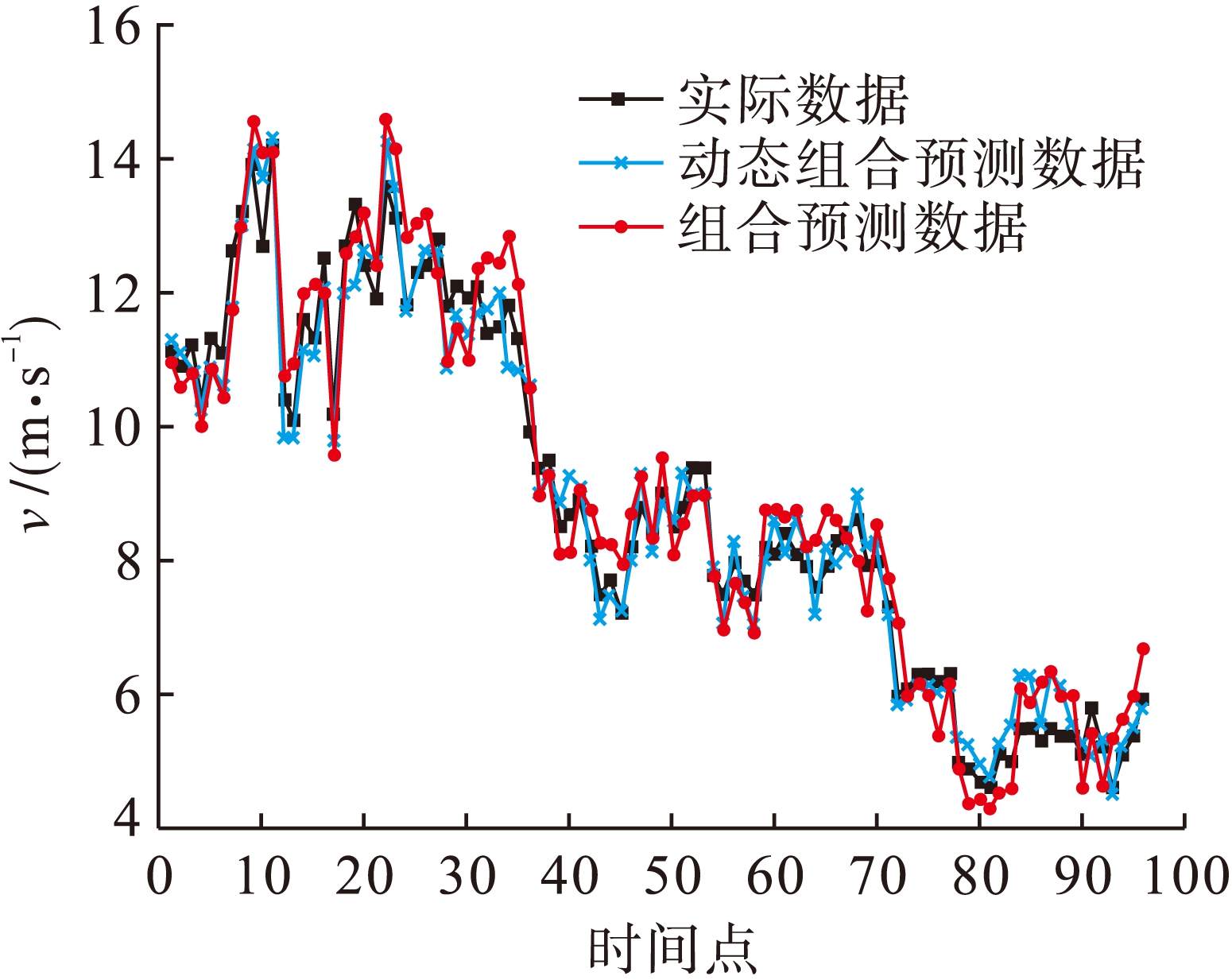
图2 组合模型预测结果
Fig.2 Forecast results of combination model
MRE BP=0.029 8>MRE GP=0.028 1>MRE DGP=0.026 9.结果表明GP模型预测效果优于单一预测模型，DGP预测精度比固定权重的GP预测精度更高一些.从图1和图2中可以看出，在风速变化比较平稳时，各个预测模型的预测精度都很好，但在风速变化比较剧烈时，所有模型精确度都有所下降，这也是风速预测难点之一.
为更好地分析模型预测效果，从图中选取一段风速变化剧烈的时间段41～60，采用RMSE和MRE对各预测模型效果进行评价，结果如表2所示.
表2 预测误差
Tab.2 Prediction error
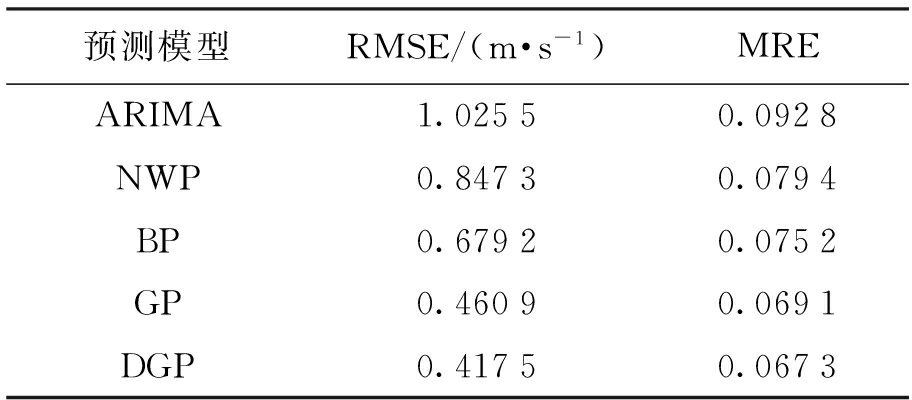
从表2中可看出，当风速变化剧烈时所有预测模型均方根误差都在增加，同时平均相对误差也会大幅增加，然而对比各模型的结果，GP精度仍然比单一模型的要好，而DGP比GP的预测精度好.
本文分析了我国风电场风速预测的现状，在不同预测模型误差的基础上，提出了动态熵权组合预测模型，并对各预测模型结果进行对比.对比结果表明，GP和DGP的预测精度要比单一模型高，而DGP与GP相比，DGP的预测精度有所提高，这也说明采用动态权值预测模型可进一步提高预测精度.在风速波动较大时，DGP预测精度要比GP预测精度高.动态熵权组合预测模型在实例中得到了验证，具有一定的实用价值.
参考文献(References)：
[1]张国强，张伯明.基于组合预测的风电场风速及风电机功率预测 [J].电力系统自动化，2009，33(18)：92-95.
(ZHANG Guo-qiang，ZHANG Bo-ming.Wind speed and wind turbine output forecast based on combination method [J].Automation of Electric Power Systems，2009，33(18)：92-95.)
[2]丁华杰，宋永华，胡泽春，等.基于风电场功率特性的日前风电预测误差概率分布研究 [J].中国电机工程学报，2013，33(34)：136-144.
(DING Hua-jie，SONG Yong-hua，HU Ze-chun，et al.Probability density function of day-ahead wind power forecast errors based on power curves of wind farms [J].Proceedings of the CSEE，2013，33(34)：136-144.)
[3]Catalao J P S，Pousinho H M I，Mendes V M F.Short-term wind power forecasting in Portugal by neural network and wavelet transform [J].Renewable Energy，2011，36(4)：1245-1251.
[4]冯双磊，王伟胜，刘纯，等.基于物理原理的风电场短期风速预测研究 [J].太阳能学报，2011，32(5)：611-616.
(FENG Shuang-lei，WANG Wei-sheng，LIU Chun，et al.Short-term wind speed prediction based on physi-cal principle [J].Acta Energiae Solaris Sinica，2011，32(5)：611-616.)
[5]蒋小亮，蒋传文，彭明鸿，等.基于时间连续性及季节周期性的风速短期组合预测方法 [J].电力系统自动化，2010，34(15)：75-79.
(JIANG Xiao-liang，JIANG Chuan-wen，PENG Ming-hong，et al.A short-term combination wind speed forecasting method considering seasonal periodicity and time-continuity [J].Automation of Electric Power Systems，2010，34(15)：75-79.)
[6]蔡凯，谭伦农，李春林，等.时间序列与神经网络法相结合的短期风速预测 [J].电网技术，2008，32(8)：82-85.
(CAI Kai，TAN Lun-nong，LI Chun-lin，et al.Short-term wind speed forecasting combing time series and neural network method [J].Power System Technology，2008，32(8)：82-85.)
[7]夏琳琳，台金娟，刘惠敏，等.权重提取与Dempster多重融合的凝汽器真空预测 [J].沈阳工业大学学报，2015，37(3)：329-334.
(XIA Lin-lin，TAI Jin-juan，LIU Hui-min，et al.Condenser vacuum prediction based on weight extraction and Dempster multiple fusion [J].Journal of Shen-yang University of Technology，2015，37(3)：329-334.)
[8]杨锡运，刘欢，张彬，等.基于熵权法的光伏输出功率组合预测模型 [J].太阳能学报，2014，35(5)：744-749.
(YANG Xi-yun，LIU Huan，ZHANG Bin，et al.A combination method for photovoltaic power forecasting based on entropy weight method [J].Acta Energiae Solaris Sinica，2014，35(5)：744-749.)
[9]刘兴杰，米增强，杨奇逊，等.基于经验模式分解和时间序列分析的风电场风速预测 [J].太阳能学报，2010，31(8)：1037-1041.
(LIU Xing-jie，MI Zeng-qiang，YANG Qi-xun，et al.Wind speed forecasting based on EMD and time-series analysis [J].Acta Energiae Solaris Sinica，2010，31(8)：1037-1041.)
[10]蒋金良，林广明.基于ARIMA的自动站风速预测 [J].控制理论与应用，2008，25(2)：374-376.
(JIANG Jin-liang，LIN Guang-ming.Automatic station wind speed forecasting based on ARIMA model [J].Control Theory & Applications，2008，25(2)：374-376.)
[11]王德明，王莉，张广明.基于遗传BP神经网络的短期风速预测模型 [J].浙江大学学报(工学报)，2012，46(5)：837-840.
(WANG De-ming，WANG Li，ZHANG Guang-ming.Short-term wind speed forecast model for wind farms based on genetic BP neural network [J].Journal of Zhejiang University (Engineering Science)，2012，46(5)：837-840.)
[12]郭琪.基于NWP的风电负荷预测方法在内蒙古电网中的应用 [D].天津：天津大学，2010.
(GUO Qi.The application of NWP-BASED wind power load prediction method in inner Mongolia po-wer grid [D].Tianjin：Tianjin University，2010.)
[13]孙培学，赵坤鹏.基于熵权法的组合模型在大坝渗流预测中的应用 [J].水电能源科学，2013，31(12)：70-73.
(SUN Pei-xue，ZHAO Kun-peng.Application of combination model based on entropy method in dam see-page forecasting [J].Water Resources and Power，2013，31(12)：70-73.)
[14]欧阳森，石怡理.改进熵权法及其在电能质量评估中的应用 [J].电力系统自动化，2013，37(21)：156-164.
(OUYANG Sen，SHI Yi-li.A new improved entropy method and its application in power quality evaluation [J].Automation of Electric Power Systems，2013，37(21)：156-164.)
(责任编辑：景 勇 英文审校：尹淑英)
LI Yong, SHI Yan-chun
(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China)
Abstract：In order to improve the accuracy of wind speed forecast in wind farm, the weights of different forecast methods were extended to weight series so as to generate the weight matrix. Meanwhile, the new forecast error was used to update the weight matrix, and the required model was obtained. Three single forecast models were established, and the forecast errors of the models in 10 days were counted, and the error series was obtained. On this basis, the dynamic entropy method was proposed. In addition, the weights of each single forecast model at 96 forecast moments were determined with the entropy weight method, and the error series and weight matrix were updated according to new 24 h forecast error so as to obtain the dynamic combination forecast model. The results show that compared with the sigle forecast model, the dynamic combination forecast model has smaller overall error index, and the forecast accuracy gets effectively improved, which proves the validity and practicability of the proposed model.
Key words：wind speed forecast; neural network; time series; numerical weather forecast; entropy weight; combination forecast; dynamic combination forecast
收稿日期：2015-11-11.
基金项目：国家自然科学基金资助项目(61102124)； 辽宁省教育厅科学技术研究项目(L2015387).
作者简介：李 勇(1980-)，男，辽宁沈阳人，讲师，博士，主要从事特种电机控制与优化、风电功率预测等方面的研究.
doi：10.7688/j.issn.1000-1646.2016.03.02
中图分类号：TK 81
文献标志码：A
文章编号：1000-1646(2016)03-0247-05
*本文已于2016-03-02 16∶42在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20160302.1642.008.html