蒋伊琳, 张芳园, 郑 辉
(哈尔滨工程大学 信息与通信工程学院, 哈尔滨 150001)
摘 要:针对小样本条件下晶振能够快速稳定实现时钟同步的问题,提出了在蒙特卡洛模拟实验下结合传统和改进后Bootstrap方法与卡尔曼滤波方法消除相关噪声,从而维持晶振稳定性的一种方法.由于传统Bootstrap方法限制再生样本的生成范围,使计算结果远远偏离真实情况,而改进Bootstrap方法可以拓展再生样本的生成范围,避免了只抽取原始数据的情况,使得频偏和时偏的估计分布尽可能地接近真实分布.仿真结果表明,改进Bootstrap对频偏和时偏的校正优于传统Bootstrap方法,利用改进Bootstrap与卡尔曼相结合的方法能够实现对晶振的快速稳定.
关 键 词:Bootstrap方法; 卡尔曼滤波; 时钟同步; 蒙特卡洛; 小样本; 再生样本; 原始数据; 估计分布
高精度的时间同步技术在通信、国防和深空探索等领域是一项关键性技术.运用该技术可以大大提高系统中时间的一致性和准确性,从而提高系统的稳定性和可靠性,满足越来越高的工程应用和科学研究的要求.
时钟在运行过程中,在不同的运行环境、温度、湿度和运行时间等条件以及晶振频率本身偏差影响,晶振的稳定度会逐步变差,时钟时间也将各不相同.为了快速实现时钟同步,对时钟的频率和偏差进行同时校正,并对晶振进行快速校正,缩短稳定时间,通常采用卡尔曼滤波的方法对晶振的时偏和频偏进行估计,但卡尔曼滤波在运行过程中需要足够多的原始数据维持系统的稳定性.在小样本条件下,卡尔曼滤波过程不能够实现对晶振的精确校正,因此,可通过Bootstrap方法获取大量的数据,再结合卡尔曼滤波,改善晶振的稳定度.
Bootstrap方法也被称为自助法,是一种通过等概率有放回模拟再抽样来分析不确定性的方法,适用于任何分布.在实际工程中,Bootstrap克服了数据有限这一困难,但在确定分布函数时只依赖于原始数据,从而自主分布产生偏离,不能接近真实情形.在这种情况下,通过扩展生成原始样本范围改进Bootstrap方法,避免了再抽样时再生数据只为原始数据这一情况,使估计分布尽可能地接近真实分布,获得高精度估计.
1.1 时偏和频偏估计
卡尔曼滤波 [1]是在信号和噪声的统计特性已知的条件下,采用高效率递归方式获得最小方差的最优估计滤波器.在IEEE1588协议 [2]条件下,采用卡尔曼滤波估计 [3]对晶振进行校正,提高同步精度.
IEEE1588协议的高同步精度建立在硬件时间戳的基础上,通过主从时钟之间时间戳信息的交换而达到同步的目的,其中,假设时间数据包的往返时延对称.图1为主从时钟的交互过程.协议把时间同步过程分为两个阶段:1)偏移测量阶段;2)延迟测量阶段.
在本文中假设往返路径对称,即数据包在传播过程中的时延相等,则有
![]()
(1)
(2)
式中:offset为主从时钟之间的时偏; T Trans1和 T Trans2分别为从时钟接收到主时钟发送Sync数据包的传播时延和主时钟接收从时钟发送Delay-Req数据包的传播时延; T m1为主时钟发送Sync数据包的时间; T s2为从时钟发送Delay-Req数据
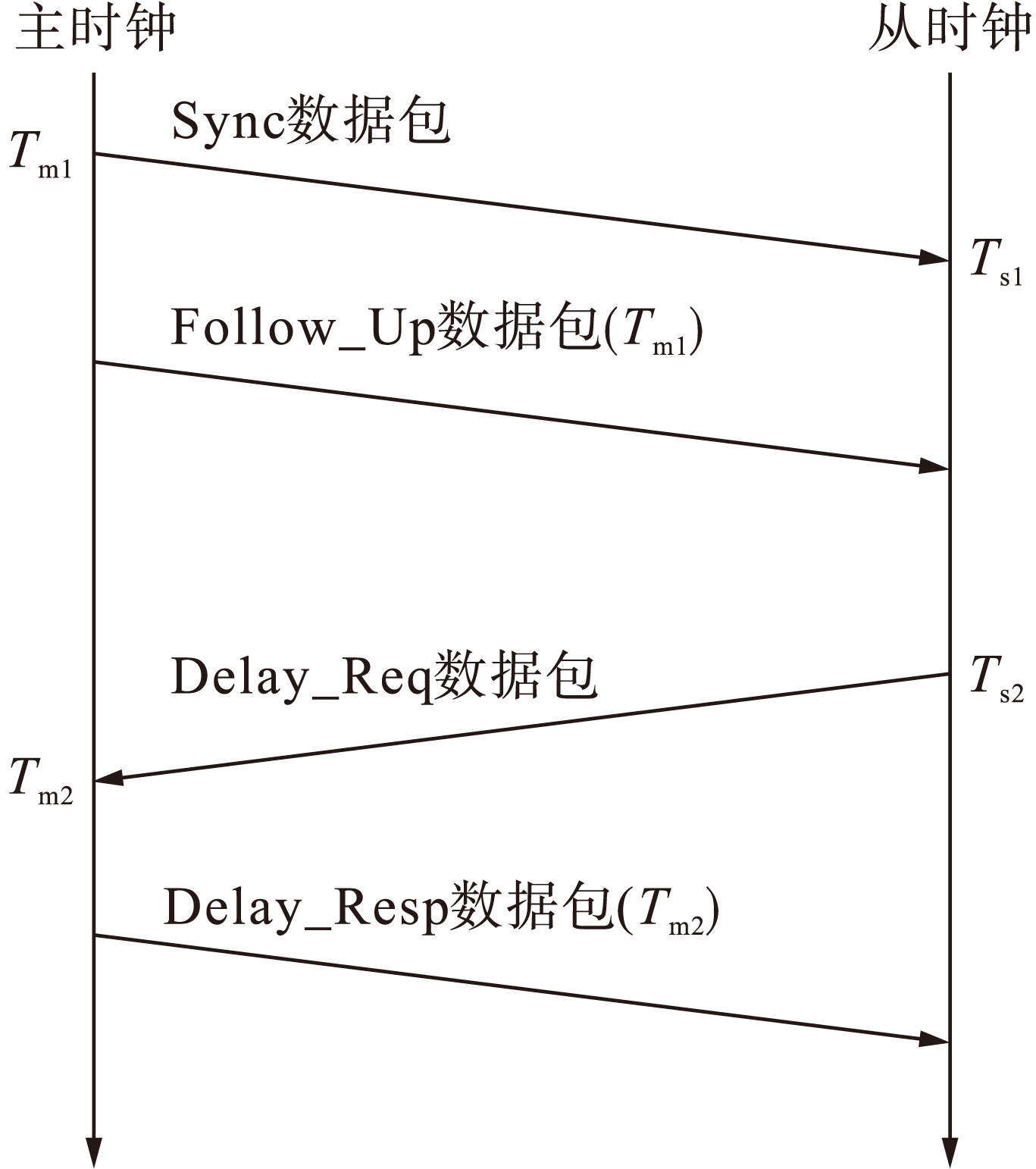
图1 主从时钟之间的交互过程
Fig.1 Interaction process between
master and slave clocks
包的时间; T s1为从时钟接收到主时钟发送的Sync数据包的时间; T m2为主时钟接收到从时钟发送的Delay-Req数据包的时间.
将式(1)、(2)进行离散化,且认为时间偏差的测量误差大小为0,则从时钟的时间偏差和频率偏差的关系式为
θ( k+1)= θ( k)- u θ ( k)+( s( k)-
u s ( k)) τ+ w θ ( k)
(3)
s( k+1)= s( k)- u s ( k)+ w s ( k)
(4)
式中: θ( k)和 s( k)为 k时刻时钟的时偏和频偏; u θ ( k)和 u s ( k)为 k时刻主从时钟实现时钟同步时,时偏和频偏的修正值; w θ ( k)和 w s ( k)为 k时刻时钟的时偏和频偏误差; τ为 k时刻采样样本的采样时间,因采样频率一定,则采样周期恒定.
设 Z( k)=[ θ( k), s( k)] T为 k时刻系统的当前状态向量, Y( k)=[ u θ ( k), u s ( k)] T为 k时刻时钟时间和频率的调整值.在同步间隔较短时认为时钟的频偏变化平稳,假定在同步间隔内频偏的变化率保持不变,即用上次同步的频偏作为同步间隔内的频偏计算下一状态的时间偏差.卡尔曼滤波的状态方程和测量方程关系式为
Z( k)= AZ( k-1)+ BY( k-1)+ W( k-1)
(5)
Y( k)= HZ( k)+ V( k)
(6)
式中: A和 B为系统参数; H为观测系统的参数; W( k-1)为 k-1时刻的系统噪声; V( k)为 k时刻的测量噪声.
根据卡尔曼滤波的递推关系式,则有如下的求解过程.
状态预测:
Z k/ k-1 = A k/ k-1 Z k-1/ k-1
(7)
状态估计:
Z k/ k = Z k/ k-1 + K k ( Y k - HZ k/ k-1 )
(8)
滤波增益:
K k = P k/ k-1 H T( HP k/ k-1 H T+ R) -1
(9)
均方误差预测:
P k/ k-1 = A k/ k-1 P k-1/ k-1 A k/ k-1 + Q
(10)
均方误差估计:
P k/ k =( I- K k H) P k/ k-1
(11)
式中: R为观测噪声方差; Q为状态转移协方差矩阵; I为单位矩阵; K为系统增益; P为状态协方差矩阵.为了尽可能消除频偏和时偏的相关噪声,通过上述迭代计算过程可提高时钟的同步精度.
本文中设置晶振为10 MHz,
τ=0.5 ms,
A=
![]() ,
,
![]()
![]() ,初始系统状态值
x=[0,2e-5],初始时偏和频偏校正值
y=[0,0].
,初始系统状态值
x=[0,2e-5],初始时偏和频偏校正值
y=[0,0].
1.2 仿真结果
通过MATLAB仿真验证上述过程,观测时间为200 s,采样间隔为0.1 s,观测点为2 000个.本文中频偏为晶振的实际频率和标准频率之间每秒产生的偏差值,通过上述求解过程对系统的频偏和时偏进行校正,提高本地时钟的稳定性和准确性,仿真图如图2所示.
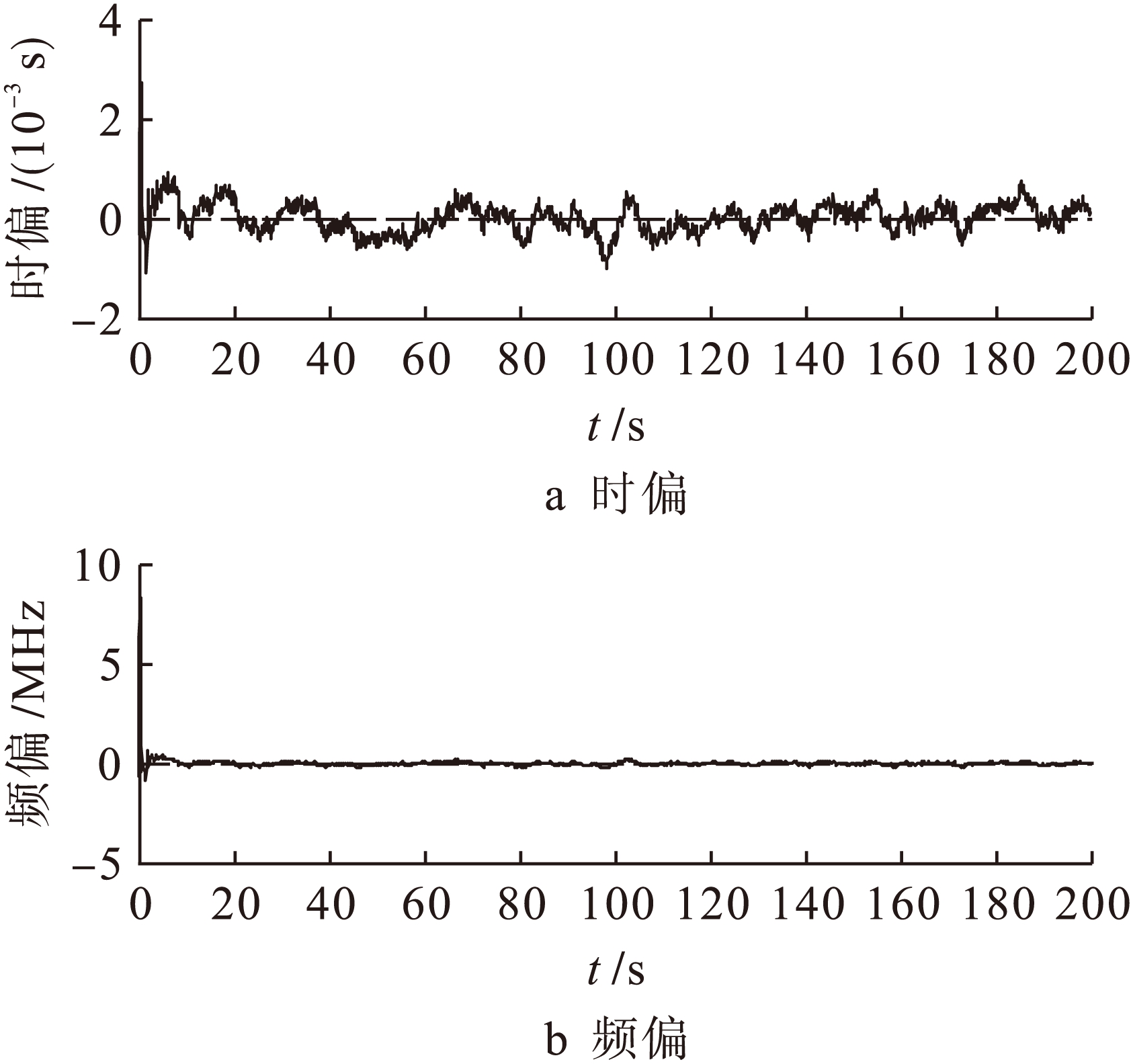
图2 时钟的时偏和频偏的状态估计值
Fig.2 State estimation values for frequency
offset and time offset of clock
由图2可知,在观测点为2 000个的条件下,卡尔曼滤波在约50 s时,频偏和时偏状态估计值趋于稳定,时偏估计精度为10 -5,频偏估计精度为10 -7.
2.1 传统Bootstrap方法
Bootstrap方法 [4-8]的核心思想是用已知的经验分布函数代替未知分布函数,即利用从原始样本中抽取的再生样本计算相关统计量,从而来估计总体分布特性.Bootstrap再抽样有3种方法,分别为参数法、半参数法和非参数法.
已知一组随机观测样本 X=( x 1, x 2,…, x N ), N为总观测点的个数, F为未知分布函数, R( X, F)是 X、 F的函数,根据原始样本 X估计随机变量 R( X, F)的分布特征.
Bootstrap方法基本步骤如下:
1) 根据已知的观测样本 X构造其经验分布函数 F n ,每个观测样本被抽取的概率为1/ N;
2) 从
F
n
中抽取再生样本
![]() ,称为Bootstrap子样本;
,称为Bootstrap子样本;
3) 根据得到的Bootstrap子样本计算相应的统计量 R b= R b( X b, F n );
4) 重复步骤2)、3)过程共 n次( n≥1 000),获得相应的 n个统计量 R b;
5) 利用 R b分布去逼近 R( X, F)分布, R b的分布被称为Bootstrap分布.
2.2 改进Bootstrap方法
Bootstrap方法作为一种统计方法被应用于许多场合,但是其也有许多的不足之处.由于再生样本是由原始样本直接生成,当原始样本数据较小时,再生样本会非常相似于原始样本,将会导致计算结果远远偏离真实情况,并且当真实分布为连续分布时,无法获取未在样本观测点处的分布特性,从而不能估计出更加接近于真实分布的分布函数.
针对上述不足,对Bootstrap方法做出了如下改进 [9-10]:
1) 将原始观测样本 X=( x 1, x 2,…, x N )按从小到大的顺序排列,结果仍记为 X=( x 1, x 2,…, x N ).
2) 对变化后的样本做出相应的邻域,即 A 1=[ x 1-( x 2- x 1)/ m, x 1+( x 2- x 1)/ m]; A i =[ x i -( x i - x i-1 )/ m, x i +( x i+1 - x i )/ m]; A N =[ x N -( x N - x N-1 )/ m, x N +( x N - x N-1 )/ m], i=2,3,…, N-1. m≥2,通常取 m=2,当样本容量过小时,即 N<10时,为避免再生样本过大偏离真实分布, m的取值应大一点.
3) 确定 L为邻域指标,其分布特性为 P( L= i)=1/ N, i=1,2,…, N.根据该分布确定邻域指标样本( l 1, l 2,…, l N ).
4) 抽取再生子样本
![]() ,得到该Bootstrap样本之后按照传统Bootstrap方法的步骤3)、4)、5)进行操作.
,得到该Bootstrap样本之后按照传统Bootstrap方法的步骤3)、4)、5)进行操作.
改进后的Bootstrap方法扩展了观测数据,避免只抽取原始数据这一情况,使估计分布尽可能地接近真实分布,提高了估计的准确性.
2.3 基于Bootstrap的卡尔曼对时偏和频偏的估计
蒙特卡洛方法 [11-12]也被称为统计模拟方法,被应用在许多计算领域且有广泛的影响.它利用随机数构建模型对各种因素进行评估,通过设定的随机过程,反复生成随机序列,计算参数估计量和统计量以及其分布特征.理论上,通过计算机的高速率和大容量计算,蒙特卡洛模拟方法随着增加的模拟次数可以获得任何精度水平的计算,并且计算误差不会随着计算维度的增加而增加.
在小样本( N=10)条件下,分别采用传统Bootstrap方法和改进Bootstrap方法对原始样本进行重采样,获得Bootstrap样本,文中假定重采样的次数为2 000次.将Bootstrap样本作为新的观测数据,采样间隔为0.01 s,卡尔曼滤波器的参数设置与上文相同.将Bootstrap样本送入卡尔曼滤波器,消除噪声影响,对晶振的时偏和频偏进行校正.在蒙特卡洛模拟实验条件下重复上述过程100次,得到传统Bootstrap和改进Bootstrap方法对晶振进行校正后时偏和频偏估计精度的集中范围.采用MATLAB仿真,得到传统和改进后的Bootstrap仿真图,如图3、4所示.
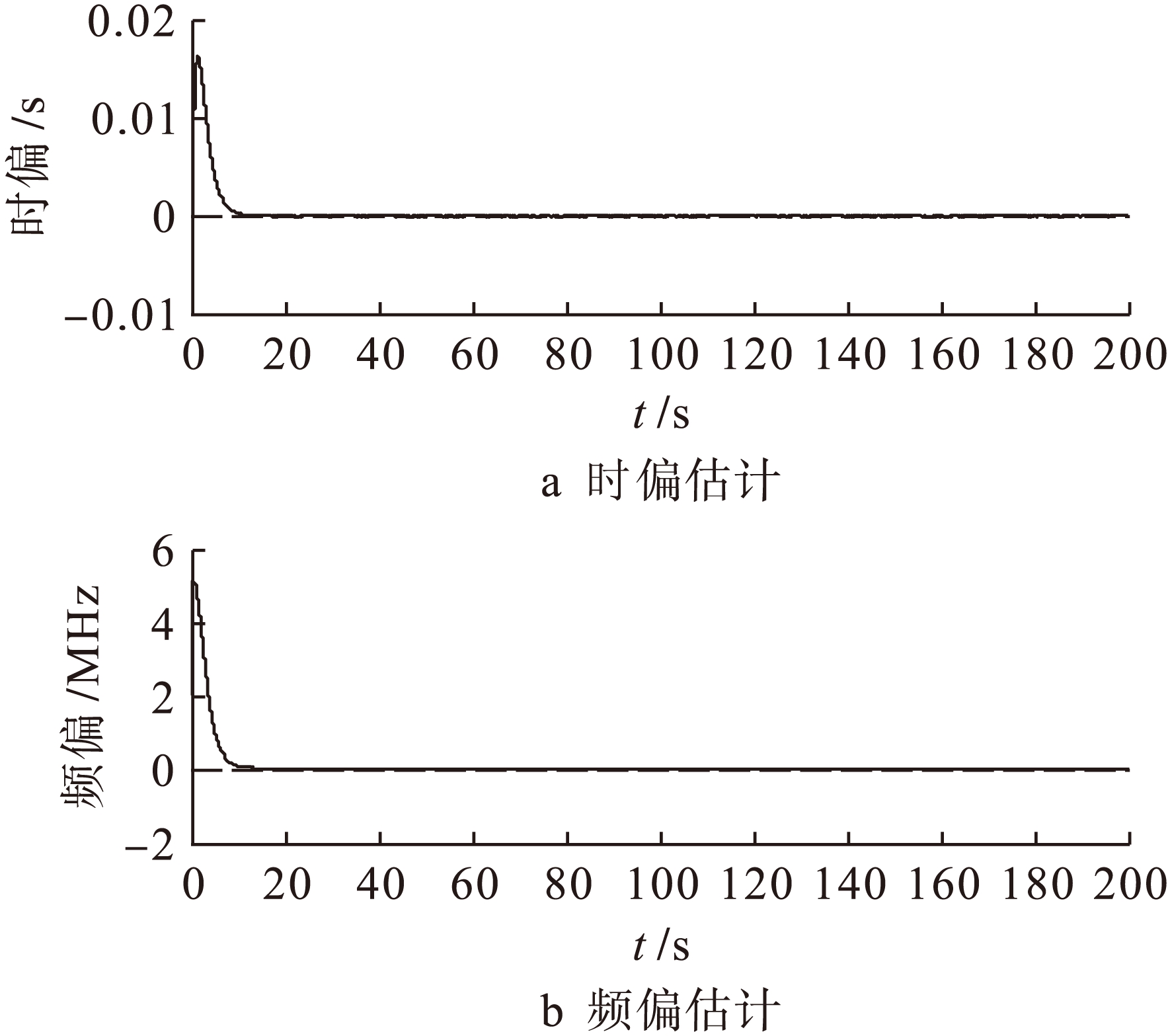
图3 传统Bootstrap采样后时钟时偏和频偏估计
Fig.3 Estimation of frequency offset and time offset of
clock after sampling of traditional Bootstrap
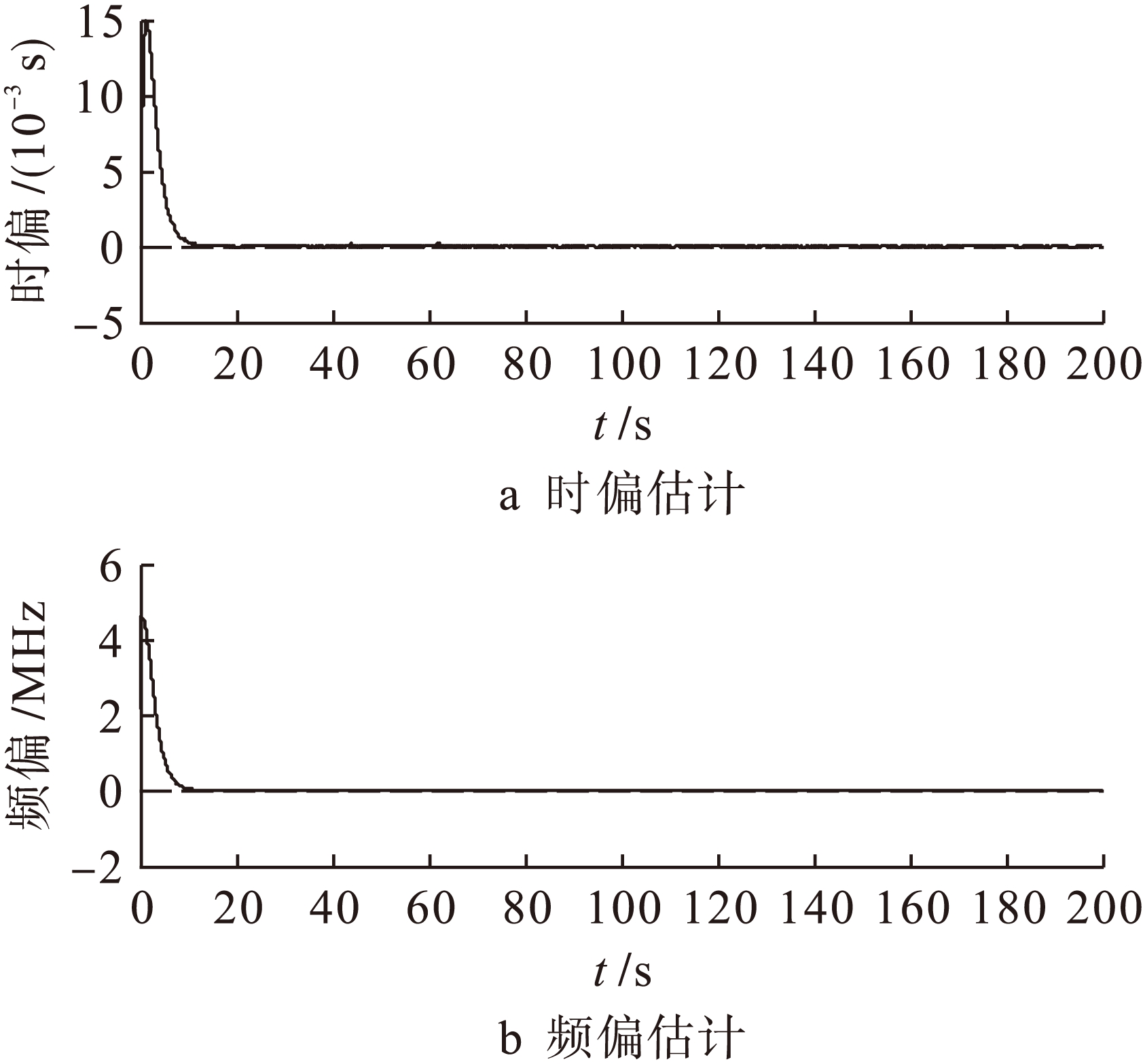
图4 改进Bootstrap采样后时钟时偏和频偏估计
Fig.4 Estimation of frequency offset and time offset of
clock after sampling of improved Bootstrap
由图3、4可知,经过Bootstrap 2 000次重采样,蒙特卡洛100次模拟实验后,传统Bootstrap方法和改进Bootstrap方法的频偏和时偏状态估计值都在约10 s时趋于稳定,而传统Bootstrap方法的时偏估计精度和频偏估计精度分别为10 -4和10 -6,改进后的Bootstrap方法的时偏和频偏估计精度少数为10 -4和10 -6,时偏和频偏估计精度绝大多数集中于10 -5和10 -7.
通过验证,改进后的Bootstrap方法虽然扩展了样本范围,使采样样本不再局限于原始数据,尽可能地使估计分布接近真实分布,提高了估计的准确性,但是其改进程度有限,不能使其分布与真实分布完全一致.经过蒙特卡洛模拟实验后,频偏和时偏的估计精度绝大多数集中于10 -5和10 -7,少数的估计精度为10 -4和10 -6.在小样本条件下,改进后的Bootstrap与卡尔曼相结合的方法在校正精度上与大样本时的卡尔曼滤波效果接近一致,且在相等的运行时间,改进Bootstrap方法能够更加快速达到稳定,缩短稳定时间,同时小样本所需要的采样时间更短.通过仿真分析可知,在观测数据为小样本时,改进Bootstrap方法与卡尔曼相结合的方法能够快速实现晶振的频偏和时偏校正,在实际应用中具有重要意义.
参考文献(References):
[1]王庆辉,鲁婷婷,刘孟龙,等.基于TOA减小非视距误差的方案设计 [J].沈阳工业大学学报,2014,36(2):204-209.
(WANG Qing-hui,LU Ting-ting,LIU Meng-long,et al.Scheme design of TOA-based system with mitigating NLOS error [J].Journal of Shenyang University of Technology,2014,36(2):204-209.)
[2]李晓珍.基于IEEE1588的网络时间同步系统研究 [D].西安:中国科学院研究生院,2011.
(LI Xiao-zhen.Research on the network time synchronization system based on IEEE1588 [D].Xi’an:Graduate School of Chinese Academy of Sciences,2011.)
[3]周思捷.基于IEEE1588无线网络时间同步技术研究 [D].上海:上海交通大学,2013.
(ZHOU Si-jie.The technology research on time synchronization in wireless network based on IEEE1588 [D].Shanghai:Shanghai Jiaotong University,2013.)
[4]吴庆平,林素仙,黄飞.非参数Bootstrap方法及其MATLAB实现 [J].丽水学院学报,2012,34(2):14-18.
(WU Qing-ping,LIN Su-xian,HUANG Fei.Non-parametric Bootstrap method and its realiztion in MATLAB [J].Journal of Lishui University,2012,34(2):14-18.)
[5]袁修开,吕震宙,岳珠峰.小样本下分位数函数的Bootstrap置信区间估计 [J].航空学报,2012,33(10):1842-1849.
(YUAN Xiu-kai,LÜ Zhen-zhou,YUE Zhu-feng.Bootstrap confidence interval of quantile function estimation for small samples [J].Acta Aeronautica et Astronutica Sinica,2012,33(10):1842-1849.)
[6]张萍.基于Bootstrap方法的统计分析 [J].宜宾学院学报,2011,11(12):31-33.
(ZHANG Ping.Statistical analysis based on Bootstrap method [J].Journal of Yibin University,2011,11(12):31-33.)
[7]孙国童,唐硕.仿真试验中Bootstrap方法的应用 [J].系统仿真学报,2010,22(6):1347-1349.
(SUN Guo-tong,TANG Shuo.Application of Bootstrap estimators in simulation experiment [J].Journal of System Simulation,2010,22(6):1347-1349.)
[8]韩冬,马进,贺仁睦.基于Bootstrap 的负荷模型的小样本不确定性分析 [J].电力系统保护与控制,2012,40(18):95-100.
(HAN Dong,MA Jin,HE Ren-mu.Small sample uncertainty analysis of load model based on Bootstrap [J].Power System Protection and Control,2012,40(18):95-100.)
[9]刘建,吴翊,谭璐.对 Bootstrap 方法的自助抽样的改进 [J].数学理论与应用,2006,26(1):69-72.
(LIU Jian,WU Yi,TAN Lu.An improvement to the resampling procedure of Bootstrap method [J].Ma-thematical Theory and Applications,2006,26(1):69-72.)
[10]邹艳,罗文强.改进的 Bootstrap 方法对比及应用研究 [J].应用数学,2008,21(增刊1):62-66.
(ZOU Yan,LUO Wen-qiang.Comparative study anel application of improved Bootstrap method [J].Ma-thematica Applicata,2008,21(Sup1):62-66.)
[11]邵伟.蒙特卡洛方法及在一些统计模型中的应用 [D].济南:山东大学,2012.
(SHAO Wei.Monte Carlo methods and their applications in some statistical model [D].Jinan:Shandong University,2012.)
[12]黄殿勋,张文,郭萍,等.发输电系统可靠性评估的蒙特卡洛改进算法 [J].电力系统保护与控制,2010,38(21):179-183.
(HUANG Dian-xun,ZHANG Wen,GUO Ping,et al.The Monte Carlo improved method for reliability eva-luation of generation and transmission systems [J].Power System Protection and Control,2010,38(21):179-183.)
(责任编辑:钟 媛 英文审校:尹淑英)
JIANG Yi-lin, ZHANG Fang-yuan, ZHENG Hui
(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)
Abstract:In order to solve the problem that the crystal oscillator can realize the fast stability and clock synchronization under the small sample condition, a method which could eliminate the correlated noise to maintain the crystal oscillator stability through combining with the traditional Bootstrap method, improved Bootstrap method and Kalman filtering method under the condition of Monte Carlo simulation experiment, was proposed. Because the traditional Bootstrap method limits the formation range of the regeneration sample, the calculated results largely deviate from the true situation. However, the improved Bootstrap method can expand the formation range of the regeneration sample, and such situation that only the original data are extracted can be avoided, which makes the estimation distribution of frequency offset and time offset be close to the real distribution. The simulated results show that the improved Bootstrap method is superior to the traditional Bootstrap method in the calibration of frequency offset and time offset. The method combined the improved Bootstrap method with the Kalman filtering method can realize the fast stability of crystal oscillator.
Key words:Bootstrap method; Kalman filtering; clock synchronization; Monte Carlo; small sample; regeneration sample; original data; estimation distribution
收稿日期:2015-08-31.
基金项目:国家自然科学基金资助项目(61202410).
作者简介:蒋伊琳(1980-),男,浙江镇江人,讲师,博士,主要从事宽带信号检测与估值、无线时间同步等方面的研究.
doi:10.7688/j.issn.1000-1646.2016.03.12
中图分类号:TM 343
文献标志码:A
文章编号:1000-1646(2016)03-0304-05
*本文已于2015-12-07 16∶18在中国知网优先数字出版. 网络出版地址: http:∥www.cnki.net/kcms/detail/21.1189.T.20151207.1618.040.html