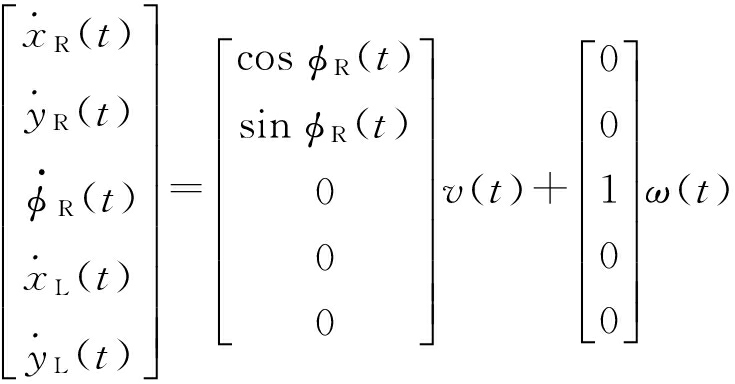⟹
张 凤， 孙 阳， 袁 帅， 李昌国， 赵岚光
(沈阳建筑大学 信息与控制工程学院， 沈阳 110168)
摘 要：针对传统EKF-SLAM算法中存在状态估计不一致的问题，从系统能观测性角度分析，提出一种增加观测性约束条件的算法，利用补偿矩阵 U最优化求解约束条件，得到新的线性点，并通过优化系统的雅克比矩阵重构系统能观测矩阵，使得EKF-SLAM系统与非线性SLAM系统观测方程能观矩阵的秩保持一致.结果表明，所提出算法在状态估计的精确性和协方差一致性方面明显优于传统的EKF-SLAM算法，研究工作和结论对车辆自主驾驶有一定的参考价值.
关 键 词：同时定位与建图； 机器人控制； 扩展卡尔曼滤波器； 能观测性分析； 最优估计； 数据融合； 估计不一致； 状态方程
移动机器人SLAM(Simultaneous localization and mapping，SLAM)是指机器人通过传感器测量值在创建环境地图同时估计自身位置和方向的方法 [1].Smith与Cheeseman [2]等人在1987年提出描述机器人与周围路标位置之间几何特征关系及其不确定性的概率方法，并首次引入随机建图策略解决SLAM问题.SLAM问题研究已经取得了飞速进展，近年来，SLAM研究的热点问题主要集中于最优估计算法设计、精确数据融合及传感器数据处理精度问题.对于在未知环境中自主驾驶的车辆，SLAM技术是车辆实现自主驾驶不可或缺的关键技术 [3-13].
在解决SLAM问题的众多算法中，EKF(Extended kalman filter，EKF)算法是应用最广泛的算法之一.Bar-Shalom等人提出：如果估计误差均值为零，并且实际协方差小于或等于滤波器估算的协方差，则状态估计是一致的，一致性是评价SLAM算法效果的主要标准.大量研究仿真实验结果 [14-19]表明：传统EKF-SLAM算法的状态估计存在不一致性，针对该问题，本文从观测方程的能观测性角度出发，分析引起传统EKF-SLAM算法产生状态不一致的本质原因，并提出一种解决方案.
通过分析传统EKF-SLAM算法中观测方程的雅克比矩阵得知该矩阵具有二维不可观测子空间，而实际上非线性系统中观测方程的雅克比矩阵具有三维不可观测子空间，分别对应全局坐标系中机器人的位置( x， y)和方向 θ，因此，传统EKF-SLAM算法的不可观测子空间与实际系统的不可观测子空间维数不一致，导致协方差估计减小不合理，使得算法估算结果出现不一致.针对此问题，本文首先提出对传统EKF-SLAM算法中观测方程的观测矩阵增加能观测性约束条件，构建补偿矩阵 U，使EKF-SLAM系统观测方程能观矩阵的秩与非线性SLAM系统观测方程能观矩阵的秩保持一致，然后，采用基于数据融合的状态延时估计方法提高 U矩阵中路标初始位置的精确度，从而改善算法估计结果，再通过对约束条件最优化求解得到算法线性化时新的线性点，并计算状态模型和观测模型的雅克比矩阵，重构系统局部能观测矩阵，最后通过仿真实验，对比传统算法与改进算法的估算结果，验证了改进算法在精确性和协方差一致性方面明显优于传统的EKF-SLAM算法.
文中以观测单一路标为例，对连续时间的非线性SLAM系统进行分析，系统状态预测方程表示为
⟹
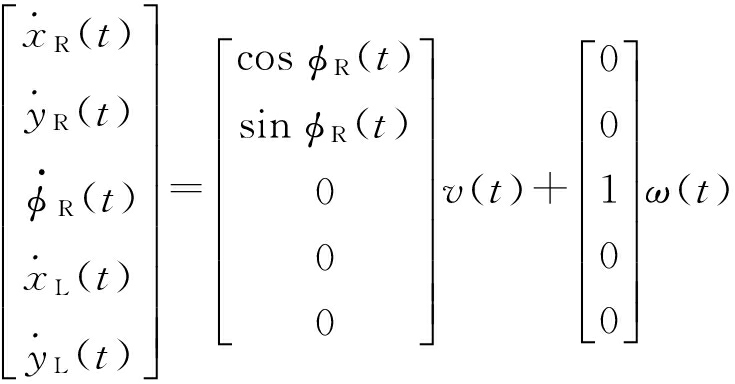(1)式中： v为线速度； ω为角速度.在传统EKF-SLAM算法中，全局坐标系下的状态变量包含机器人位姿以及路标位置. k时刻状态变量定义为
(2)
式中
，
φ
R
k
]
T为机器人位姿；
P
L为路标位置；
P
R
k
为机器人在
k时刻的位置；
φ
R
k
为机器人在
k时刻的航向.
移动机器人定位系统的预测方程及观测方程可以表示为
x k = f( x k-1 ， k-1)+ Γ( x k-1 ， k-1) w k-1
(3)
z k = h( x k ， k)+ v k
(4)
式中： w k 、 v k 为零均值白噪声序列； f、 h、 Γ为任意测量函数； z k 为与相对距离和偏转角度相关的测量值，可由测距传感器获得.
1.1 EKF预测
预测过程主要是利用预测模型更新预测方程中当前状态的先验值，实时推算下一时刻的状态变量和误差协方差，以便为下一个时刻最优化估算奠定基础.由于路标位置不发生变化，EKF预测方程形式为
(5)
R
k+1
(6)
(7)
式中
与
分别表示机器人和地标的估计位置；
C(·)为2×2的旋转矩阵；
R为机器人航向的估计值，
R
k+1
分别为机器人从
k时刻到
k+1时航向和位置的变化量；状态变量下标的通式为
形式，代表利用状态
j时刻值估算
l时刻值.
算法非线性模型的状态预测方程为
(8)
式中，
为机器人从
k时刻到
k+1时刻的变化量预测估计值，其中包含零均值的高斯白噪声
R
k+1
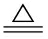
.对该模型线性化后，线性误差状态预测方程变换为
(9)
式中
为任意状态变量
x的估计值；
，为估计量的误差；0
m×
n
为
m×
n阶零阵；
I
n
为
n×
n单位矩阵；
Φ
R
k
，
G
R
k
分别为关于状态和预测的噪声雅克比矩阵，
Φ
R
k
由状态预测方程(2)、(3)获得，即
(10)
(11)
式中，
，该矩阵适用于任何机器人运动模型(独轮车，自行车，阿尔曼模型)，具有广义性.
1.2 EKF更新
EKF更新是通过预测方程与观测方程对系统状态变量进行最优估计.预测方程已经在上文进行了说明，观测方程描述的是机器人与周围环境路标相对距离的观测值.在 EKF更新时，利用预测方程的先验值与当前路标观测的测量值以及测量协方差对机器人位姿状态进行最优估计，即
z k=h(x k)+v k=h( R k P L )+v k
(12)
式中， R k P L =C T (φ R k )(P L -P R k )，为k时刻路标相对于机器人的位置.测量函数是非线性的，首先进行线性化处理，线性测量误差方程描述为
(13)
式中，H R k ，H L k 为关于h的雅克比矩阵，分别对应机器人位姿和路标位置，表示为
H
R
k
= (
(14)
H
L
k
=(
(15)
式中，
h
k为机器人相对于路标位置间距的雅克比矩阵，通过式(12)在状态估计
上计算偏导数获得.
2.1 非线性SLAM系统能观测性分析
根据 Hermann和 Krener提出 EKF- SLAM观测方程的能观测性秩条件，对连续时间条件下的非线性 SLAM系统进行能观测性分析.机器人位姿状态模型采用式(1)，测量值是路标与机器人之间的相对位置，观测模型表示为
z(t)=h(ρ，ψ)
(16)
(17)
ψ=a tan2(y L -y R ，x L -x R )-φ R
(18)
式中，ρ和ψ为机器人与路标的相对距离和相对方位角度，二者之间的相对距离关系表示为
(19)
则观测模型可表示为
z(t)= C T φ R (t)(P L (t)-P R (t))=
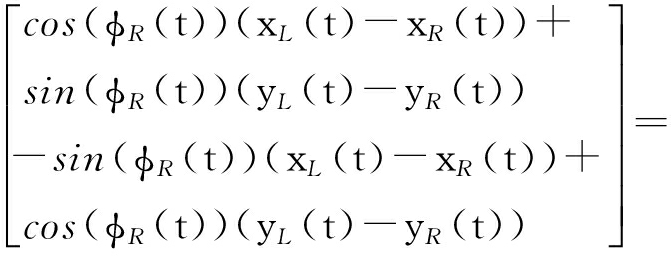
(20)
针对式(20)，采用李导数方法计算能观测矩阵.由计算结果分析可知，n阶李导数和一阶李导数具有线性关系，为计算方便，采用一阶李导数计算能观测矩阵，去掉全0行，得到观测矩阵为
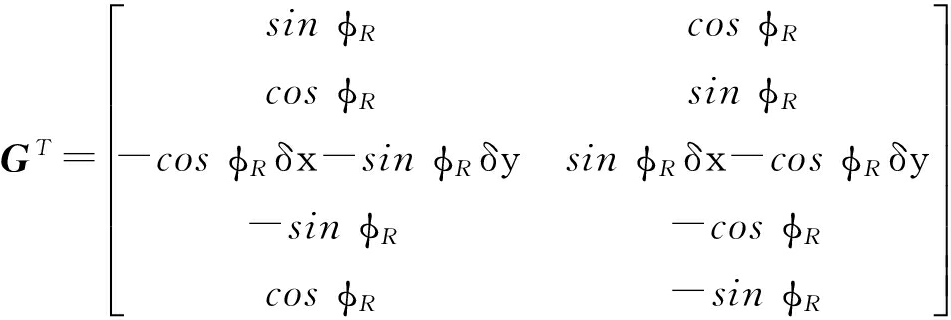
(21)
式中：δx
x
L
-x
R
；δy
y
L
-y
R
.式(21)的一个基础解系为
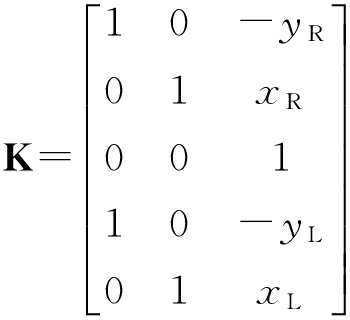
(22)
式(21)是一个非满秩矩阵，具有三个不可观测自由度，即机器人在全局坐标系下的状态向量(位置与方向)在SLAM系统方程中是不可观测的.
2.2 EKF-SLAM能观测性分析
由式(21)可知，非线性SLAM系统观测方程具有三个不可观测自由度，理论上应用EKF算法对SLAM系统线性化后，系统应仍然具有三个不可观测自由度.分别对理想EKF-SLAM系统和传统EKF-SLAM系统观测方程的观测矩阵维数进行分析.
采用观测矩阵对时变线性化误差状态系统进行能观测性分析， k到 k+ i时刻的观测矩阵定义为
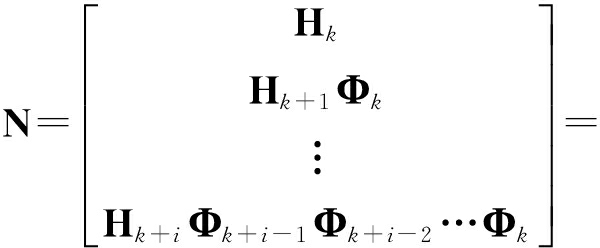
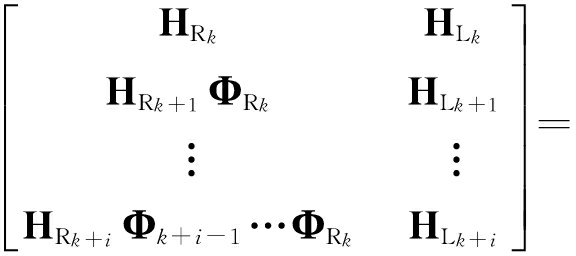
Diag( H L k ， H L k+1 ，…， H L k+ i )·
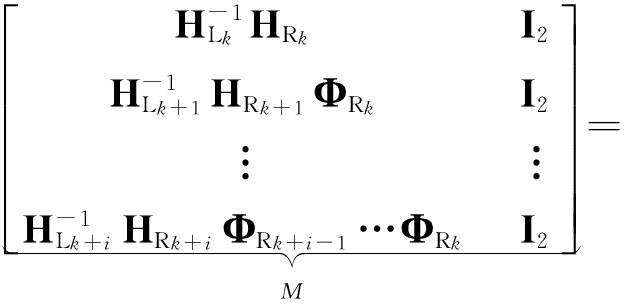
(23)
Diag(·)是一个区块对角阵，当且仅当局部观测矩阵 N是满秩矩阵时，系统从 k到 k+ i时刻是局部能观的.矩阵Diag( H L k ， H L k+1 ，…， H L k+ i )是非奇异的，显而易见，Rank( N)=Rank( M)，矩阵 N和 M具有相同的秩，因此，分析矩阵 M与分析矩阵 N具有相同的意义.同时根据式(23)也可以得到观测矩阵是一个关于线性点的函数，线性点选取精度对EKF线性误差状态方程的能观测性产生影响.
2.3 理想EKF-SLAM
在理想情况下，EKF-SLAM线性点取值为系统状态变量的真实值，即
(24)
由此观测矩阵可表示为
[- I 2，- J( P L- P R k )]
(25)
N= Diag( H L k ， H L k+1 ，…， H L k+ i )·
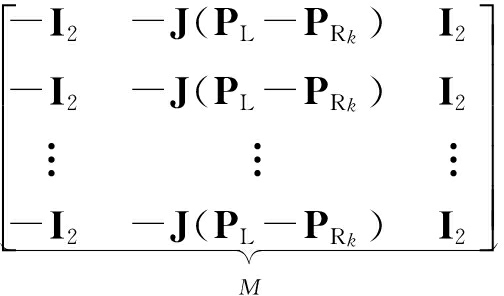
(26)
根据rank( M)=2得到rank( N)=2，理想EKF-SLAM系统的局部观测矩阵秩为2，具有三个不可观测自由度.
2.4 传统EKF-SLAM
传统的EKF-SLAM的线性化点取在系统状态变量的最优估计值处，则有
Φ R k+i-1 …Φ R k+1 Φ R k =
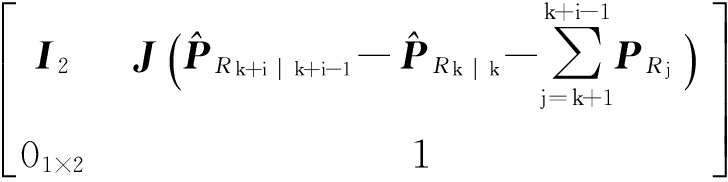
(27)
由此观测矩阵可表示为
(28)
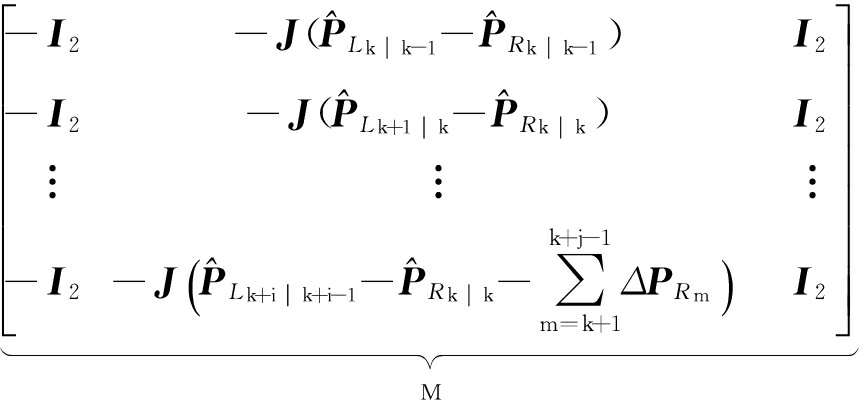
(29)
根据rank( M)=3得到rank( N)=3，则理想EKF-SLAM系统的观测矩阵秩为3，具有两个不可观测自由度.因此传统EKF-SLAM算法在估计值位置估算的雅克比矩阵比理想SLAM系统中雅克比矩阵的观测维数多了一维，引入虚假信息，导致系统状态估计不一致.
为了使传统EKF算法线性化后的SLAM系统中观测方程的能观矩阵秩保持不变，增加了能观测约束条件，通过补充 U矩阵重构观测矩阵，实现线性化前后的SLAM系统观测矩阵秩不变.同时为了改善 U矩阵的补偿效果，采用基于数据融合的路标位置延时状态估计与最优选取线性点位置的方法重构观测矩阵.
3.1 增加能观测性约束条件的U矩阵补偿
定理1 如果EKF雅克比矩阵是通过线性点
和
计算得到，则表达式
Φ
k
=
满足如下条件
(30)
通过增加能观测性约束条件，引入5×3的满秩矩阵 U，SLAM系统观测矩阵的秩由3降为2，实现了线性化前后的SLAM系统具有相同的不可观测自由度维数.
证明 当SLAM系统满足式(30)时，观测矩阵所有行具有相同的不可观测向量个数，该数量与 U的列数相同.机器人和路标的真实位置在未知环境中不能获得，因此，选取路标和机器人第一次被估计位置分别作为路标和机器人的初始位置，仿照式(22)构造 U矩阵.
当系统观测单一路标时， U的表达式为
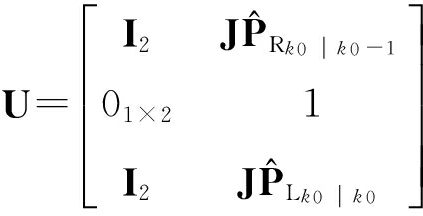
(31)
当系统同时观测 M个路标时， U的表达式为
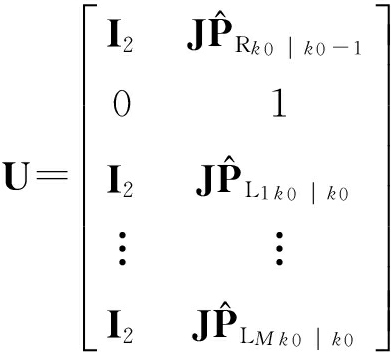
(32)
3.2 基于数据融合的路标位置延时状态估计
传感器测量误差会降低路标位置的初始估计精度，而直接使用此测量数据，会引入较大误差.通过基于数据融合的延时状态估计方法估算路标位置初始值将提高其计算精度.
机器人在( x 1， y 1)，( x 2， y 2)两个位置分别观测同一个特征( x， y)，观测值分别为 r 1， r 2，则相应观测路标的位置为 P L 1 ( x L 1 ， y L 1 )， P L 2 ( x L 2 ， y L 2 ).若定义两个圆方程为
(33)
则求得
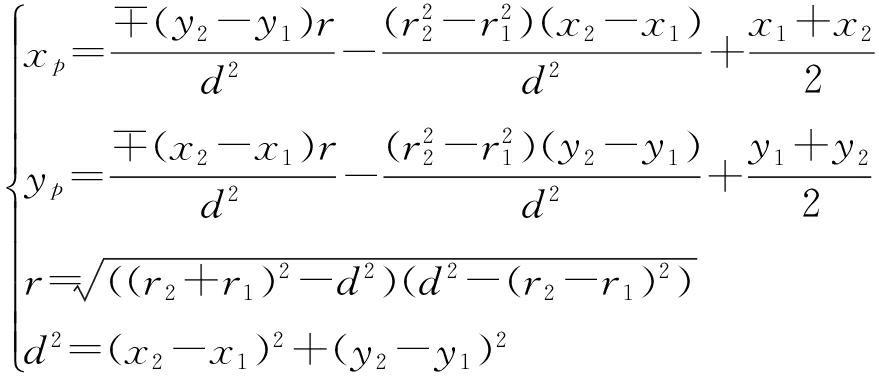
(34)
设定路标初始位置为
P
L
1
，协方差为
C
L
1
，经延时状态估计处理后，路标位置更新为
，协方差更新为
.通过融合两次的路标位置得到位置
及协方差
，将其作为新的路标初始值，即
(35)
3.3 线性化点最优选取
线性化误差最优选取点可表示为
(36)
并服从于
(37)
选取 x *为线性点，并采用泰勒级数展开式
f( x)= f( x *)+ f′( x *)( x- x *)+
(38)式中，泰勒级数展开式的余项
(
x-
x
*)
2为线性化误差项，变量
ζ取值范围为
ζ∈(
x，
x
*).因此，最小化线性化误差等价于
(39)
根据二阶导数的几何意义，特征量表征了运动曲线的曲率.考虑到机器人运动轨迹的平滑性，运动曲线的曲率较小，若略去 f″( ζ)对式(38)的影响，主要考虑( x- x *) 2项，则式(38)可表示为
⟺min((
x-
x
*)
2)
(40)
本实验以MATLAB为平台，在Tim Bailey等人提供的EKF-SLAM平台基础上进行程序设计，实现上述算法功能.仿真基于200 m×200 m的室内环境，图1和图2分别为同一环境条件下采用传统算法与本文算法进行实验仿真的小车运动路径(星号为地标的理想位置，加号为经标准卡尔曼滤波算法获得的估计位置，粗线表示机器人估计路径，细线表示机器人预计路径).
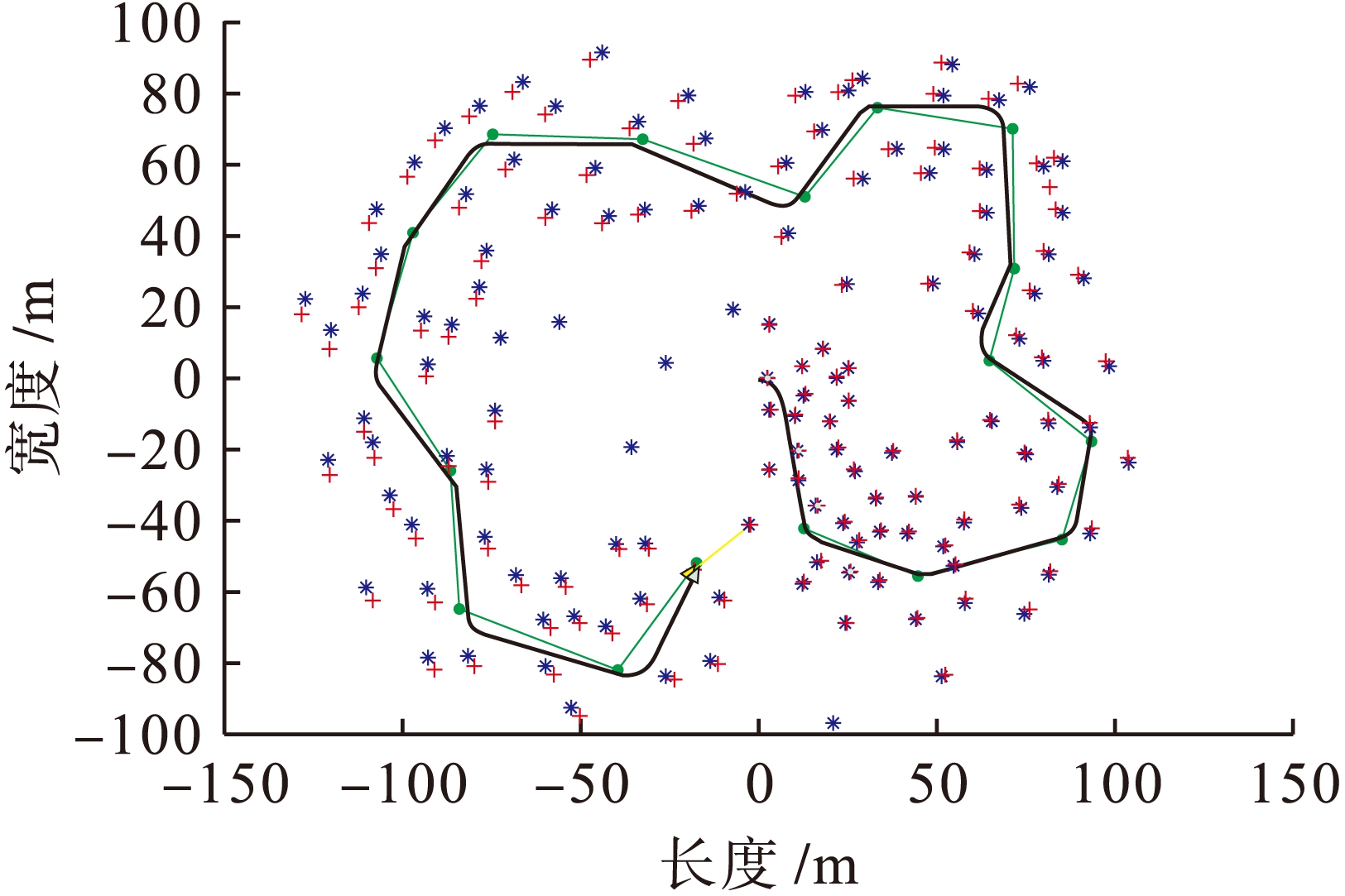
图1 EKF-SLAM仿真结果
Fig.1 Simulated results of EKF-SLAM
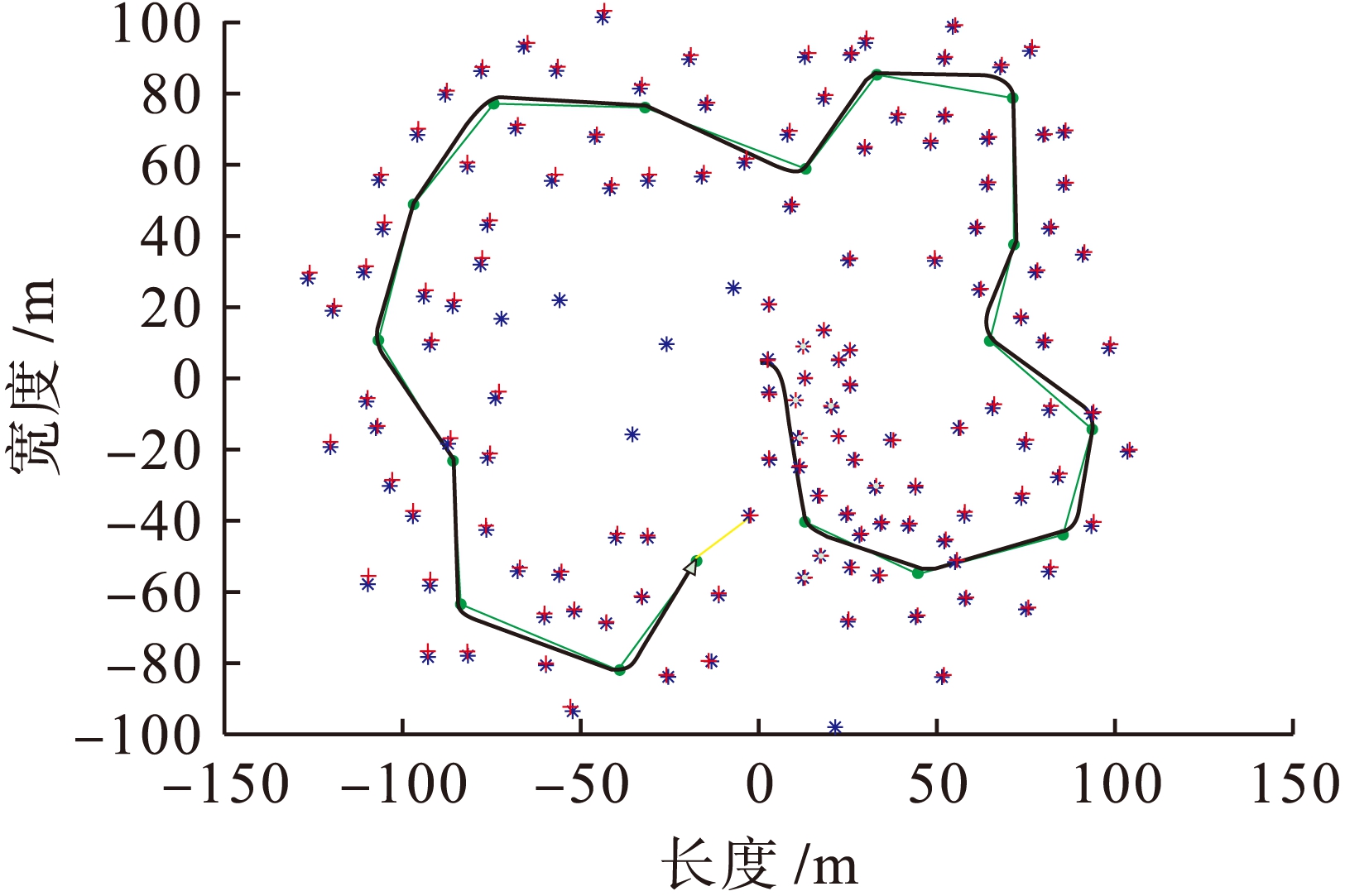
图2 改进EKF-SLAM仿真结果
Fig.2 Simulated results of modified EKF-SLAM
图2与图1相比，路标位置的估计值更加靠近路标真实值.当采用传统EKF-SLAM算法时，随着小车不断运动，算法线性化误差不断累计增加，路标位置的观测和小车自身位姿的估计误差不断积累，与预计值的偏离误差较大.而本文提出的算法明显提高了路标位置与机器人位姿的估计精度.
定义SLAM位置误差为
，定位的姿态角误差为
，改进前后的位置误差曲线与角度误差曲线如图3、4所示(图中星号为标准卡尔曼滤波算法的误差，圆圈为改进卡尔曼滤波算法的误差).
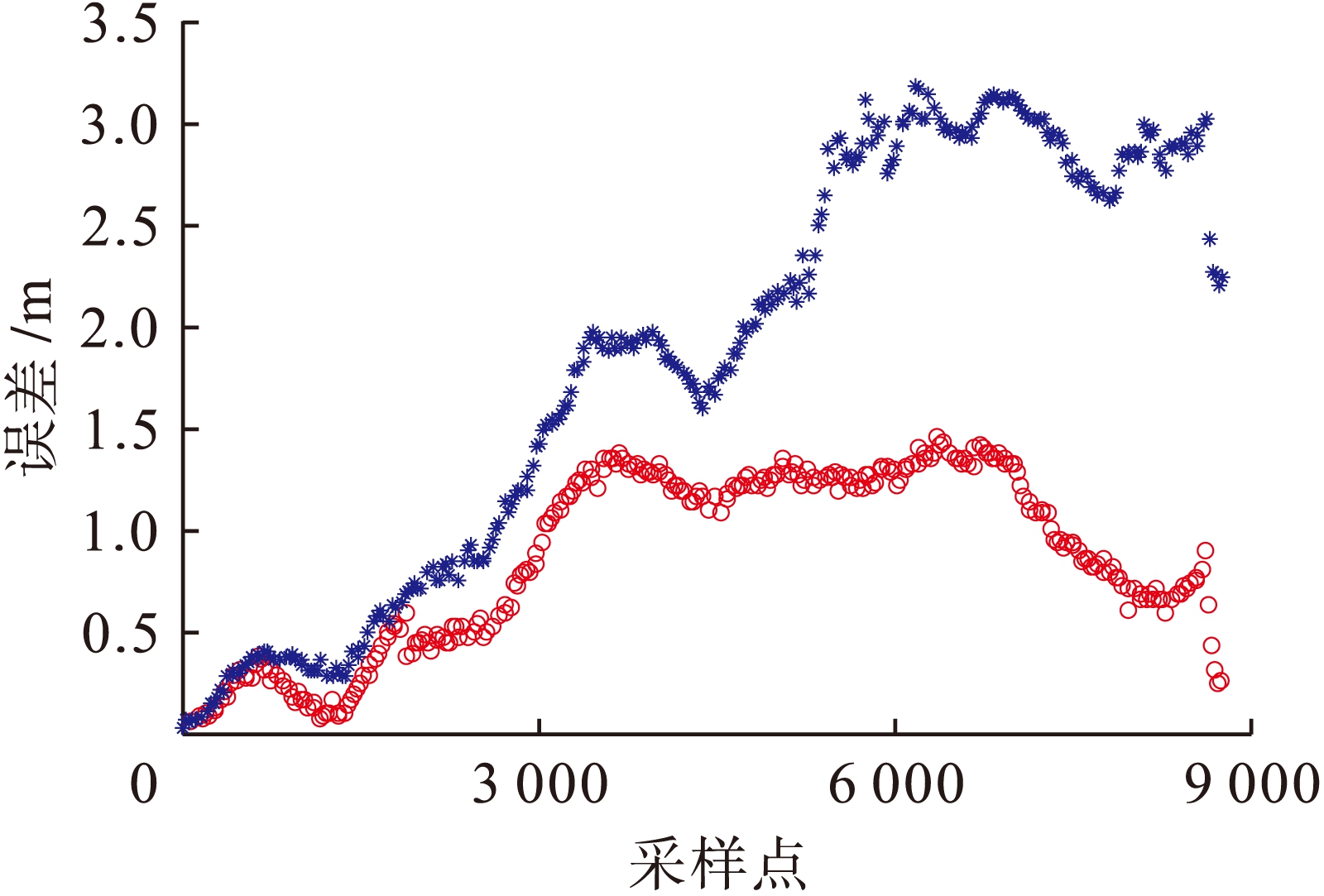
图3 位置估计偏差
Fig.3 Deviation of position estimation
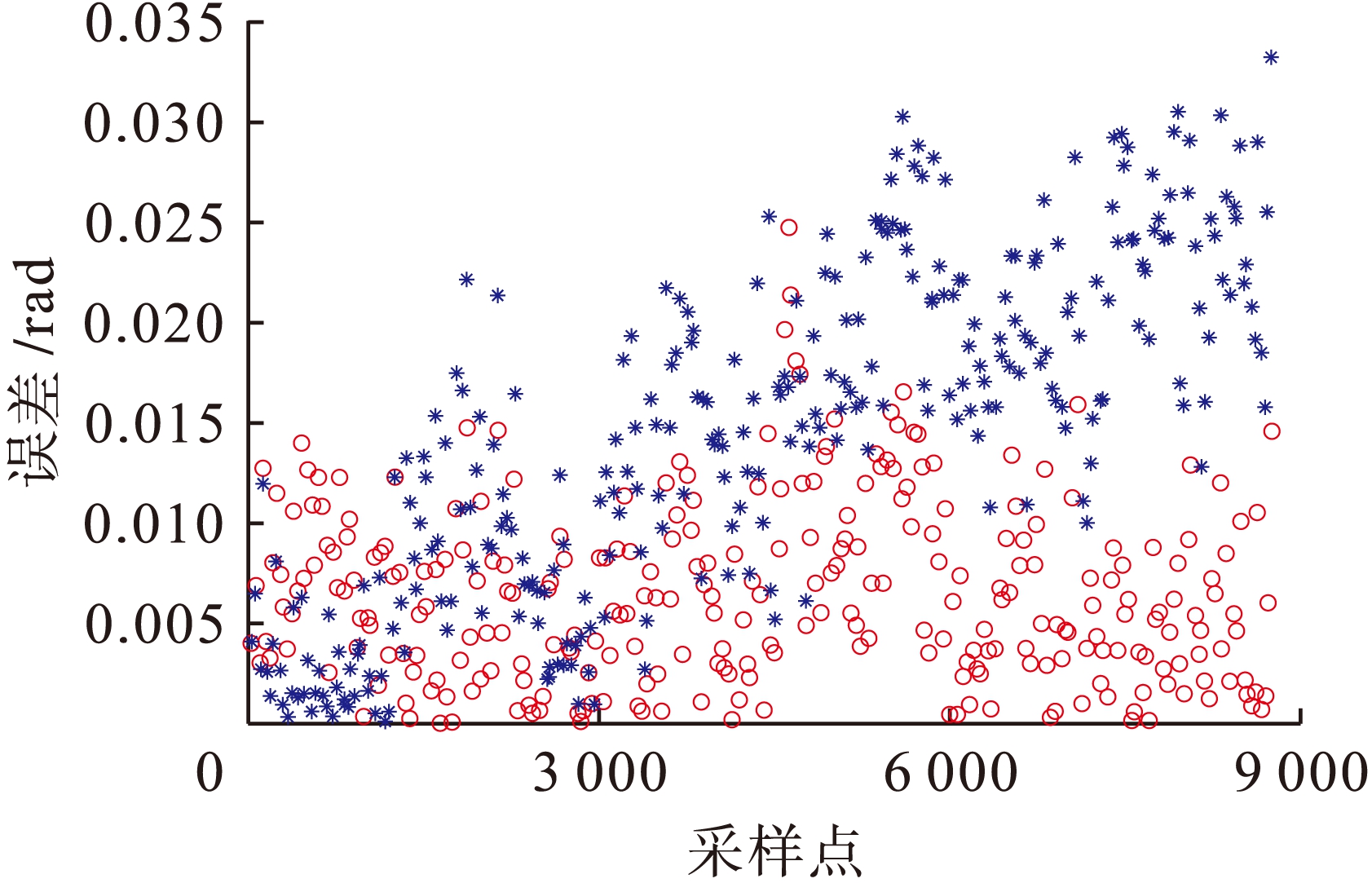
图4 EKF-SLAM航向偏差
Fig.4 Course deviation of EKF-SLAM
从图3中可以看出，本文所提算法的位置偏差明显低于传统EKF-SLAM算法.由此表明，附加的能观测性限制及初始化有效提高了机器人位置的估计精度.图4说明本文所提的算法改善了传统EKF-SLAM算法中存在的状态估计不一致问题.
机器人状态协方差是衡量估计精度的重要指标，随机选取10组本文算法和EKF-SLAM算法的机器人状态协方差进行比较，结果如表1所示.
表1 机器人状态协方差
Tab.1 State covariance of robot
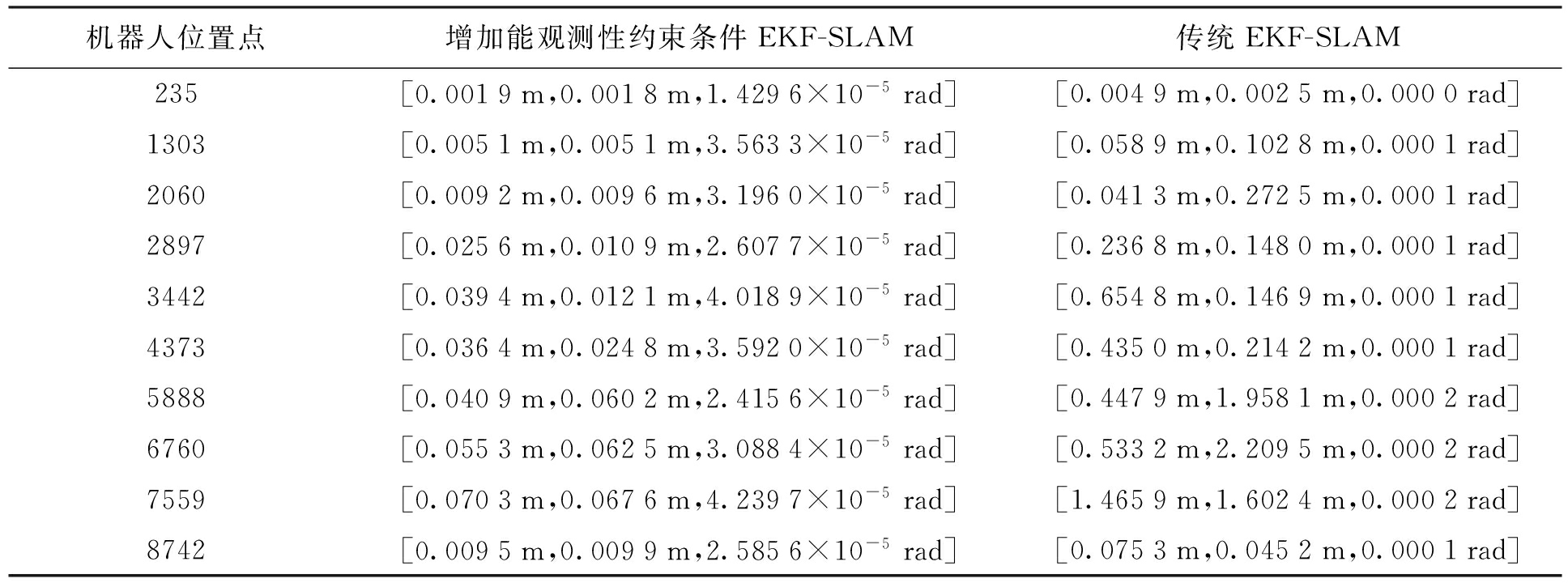
从表1可以看出，本文提出的算法减小了机器人的协方差矩阵，即降低了机器人位置估计的不确定性，估计精度高于传统EKF-SLAM.
传统EKF-SLAM的状态观测方程具有二维不可观测子空间，而SLAM非线性系统的状态观测方程具有三维不可观测子空间，这是导致传统EKF滤波算法估算结果不一致的主要因素.本文通过增加能观测性约束条件的U矩阵补偿，采用基于数据融合的路标位置延时状态估计方法，实现了线性化点最优选取与观测矩阵重构.仿真实验结果说明，EKF系统的能观测性会影响系统估算结果的一致性，同时验证了本文提出算法在状态估计精度和方差一致性方面优于传统EKF-SLAM算法，有效提高了建图与定位的精度.
参考文献(References)：
[1]陈长征，项宏伟，杨孔硕，等.可变形履带机器人跨越台阶的动力学分析 [J].沈阳工业大学学报，2015，37(2)：165-170.
(CHEN Chang-zheng，XIANG Hong-wei，YANG Kong-shuo，et al.Dynamic analysis for variable tracked robot in process of climbing steps [J].Journal of Shenyang University of Technology，2015，37(2)：165-170.)
[2]Smith R，Cheeseman P.On the representation and estimation of spatial uncertainty [J].The International Journal of Robotics Research，1987，5(4)：56-68.
[3]Kim S J，Kim B K.Dynamic ultrasonic hybrid localization system for indoor mobile robots [J].IEEE Transactions on Industrial Electronics，2013，60(10)：4562-4573.
[4]Guerreiro B J N，Batista P，Silvestre C，et al.Globally asymptotically stable sensor-based simultaneous locali-zation and mapping [J].IEEE Transactions on Robotics，2013，29(6)：1380-1395.
[5]Auat F A，Pereira F M L，Sciascio F，et al.Autonomous simultaneous localization and mapping driven by Monte Carlo uncertainty maps-based navigation [J].The Knowledge Engineering Review，2013，28(1)：35-57.
[6]Souici A，Courdesses M，Ouldali A，et al.Full-observability analysis and implementation of the general SLAM model [J].International Journal of Systems Science，2013，44(3)：568-581.
[7]Oh S，Hahn M，Kim J.Simultaneous localization and mapping for mobile robots in dynamic environments [C]//International Conference on Information Science and Applications.Pattaya，Thailand，2013：1-4.
[8]Lee D，Kim D，Lee S，et al.Experiments on localization of an AUV using graph-based SLAM [C]//10th International Conference on Ubiquitous Robots and Ambient Intelligence.Jeju，Korea，2013：526-527.
[9]Lourenço P，Guerreiro B J，Batista P，et al.Preliminary results on globally asymptotically stable simultaneous localization and mapping in 3-D [C]//American Control Conference (ACC).Washington D C，America，2013：3087-3092.
[10]Pailhas Y，Capus C，Brown K，et al.Design of artificial landmarks for underwater simultaneous localisation and mapping [J].IET Radar，Sonar & Navigation，2013，7(1)：10-18.
[11]Yoon S，Hyung S，Lee M，et al.Real-time 3D simultaneous localization and map-building for a dynamic walking humanoid robot [J].Advanced Robotics，2013，27(10)：759-772.
[12]Ceriani S，Marzorati D，Matteucci M，et al.Single and multi-camera simultaneous localization and mapping using the extended Kalman filter [J].Journal of Mathematical Modelling and Algorithms in Operations Research，2014，13(1)：23.
[13]Chen Z，Dai X，Jiang L H，et al.Adaptive iterated square-root cubature Kalman filter and its application to SLAM of a mobile robot [J].Journal of Electrical Engineering，2013，11(12)：7213-7221.
[14]Oguz A E，Temeltas H.On the consistency analysis of A-SLAM for UAV navigation [C]//International Society for Optics and Photonics.Baltimore，USA，2014：90840R-90840R-12.
[15]Castellanos J A，Martinez C R，Tardós J D，et al.Robocentric map joining：improving the consistency of EKF-SLAM [J].Robotics and Autonomous Systems，2007，55(1)：21-29.
[16]Huang S，Dissanayake G.Convergence and consistency analysis for extended Kalman filter based SLAM [J].IEEE Transactions on Robotics，2007，23(5)：1036-1049.
[17]Huang G P，Mourikis A，Roumeliotis S.A quadratic-complexity observability-constrained unscented Kalman filter for SLAM [J].IEEE Transactions on Robotics，2013，29(5)：1226-1243.
[18]Chen S Y.Kalman filter for robot vision：a survey [J].IEEE Transactions on Industrial Electronics，2012，59(11)：4409-4420.
[19]Gamage D，Drummond T.Reduced dimensionality extended Kalman filter for SLAM [C]//The 24th British Machine Vision Conference (BMVC 2013).Bristol，Britain，2013：1-11.
(责任编辑：景 勇 英文审校：尹淑英)
ZHANG Feng, SUN Yang, YUAN Shuai, LI Chang-guo, ZHAO Lan-guang
(Information &Control Engineering Faculty, Shenyang Jianzhu University, Shenyang 110168, China)
Abstract：In order to solve the problem that the state estimation inconsistency exists in the traditional EKF-SLAM (extended Kalman filter-simultaneous localization and mapping) algorithm, an algorithm which could increase the observability constraint condition was proposed from the perspective of system observability. In addition, the compensation matrix Uwas optimized to solve the constrained condition, and the new linear points were obtained. Through optimizing the Jacobi matrix of system, the observability matrix of system was reconstructed, which could make the rank of local observability matrix of EKF-SLAM system be consistent with that of non-linear SLAM system. The results show that the proposed algorithm is superior to the traditional EKF-SLAM algorithm in terms of both state estimation accuracy and covariance consistency. The research work and conclusions have certain reference value for the vehicle autonomous driving.
Key words：simultaneous localization and mapping; robot control; extended Kalman filter; observability analysis; optimal estimation; data fusion; estimate inconsistency; state equation
收稿日期：2015-08-04.
基金项目：国家青年基金资助项目(61305125).
作者简介：张 凤(1972-)，女，辽宁沈阳人，副教授，主要从事移动机器人控制技术和智能控制等方面的研究.
doi：10.7688/j.issn.1000-1646.2016.03.15
中图分类号：TP 242.6
文献标志码：A
文章编号：1000-1646(2016)03-0319-07
*本文已于2016-03-02 16∶48在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20160302.1648.054.html
控制工程