王 颖,易 坤
(沈阳工业大学 建筑与土木工程学院,沈阳 110870)
摘 要:为了对比分析方钢管混凝土柱![]() 工字钢梁和方空钢管柱
工字钢梁和方空钢管柱![]() 工字钢梁两种框架结构的力学性能,运用有限元软件分别对上述两种框架结构进行了全尺寸建模,完成非线性有限元计算分析.结果表明,计算结果与实验数据吻合较好,验证了所建模型的准确性;两种框架结构的滞回曲线均为饱满的梭形,无明显的捏缩现象,且方钢管混凝土柱
工字钢梁两种框架结构的力学性能,运用有限元软件分别对上述两种框架结构进行了全尺寸建模,完成非线性有限元计算分析.结果表明,计算结果与实验数据吻合较好,验证了所建模型的准确性;两种框架结构的滞回曲线均为饱满的梭形,无明显的捏缩现象,且方钢管混凝土柱![]() 工字钢梁框架梁端水平极限承载力高于方空钢管柱
工字钢梁框架梁端水平极限承载力高于方空钢管柱![]() 工字钢梁框架结构.
工字钢梁框架结构.
关 键 词:钢管混凝土柱;空钢管柱;框架;工字钢梁;外加强环;节点;有限元;力学性能
方钢管混凝土框架结构具有节点简单、加工方便、施工周期短和便于采取防火板材等优点,在高层、超高层建筑中的应用越来越广泛.到目前为止,国内外针对钢管混凝土单个构件方面进行了较多研究,并对钢管混凝土节点进行了研究,相比之下,对于钢管混凝土框架结构上的研究较少[1-3].工程上复杂的多层多跨框架结构都是由简单的单层单跨结构组合而成,因此,对单层单跨结构整体上进行研究非常必要.在实际试验分析研究过程中,不仅试验费用较高,耗时费力,而且存在诸多试验不确定性因素影响,易造成试验与实际情况存在偏差.拥有强大工程模拟功能的有限元软件ABAQUS带来了一种更加高效、便捷、经济的研究分析方法.本文根据王文达博士的实际试验数据[4],利用有限元软件ABAQUS对方钢管混凝土柱![]() 工字钢梁框架进行低周循环荷载作用下的力学性能分析,并与试验结果进行对比,从而验证所建立的有限元计算模型的准确性.在此基础上,对方空钢管柱
工字钢梁框架进行低周循环荷载作用下的力学性能分析,并与试验结果进行对比,从而验证所建立的有限元计算模型的准确性.在此基础上,对方空钢管柱![]() 工字钢梁框架结构进行低周循环荷载作用下的力学性能分析,并对两种组合结构的梁柱框架结构进行对比分析.
工字钢梁框架结构进行低周循环荷载作用下的力学性能分析,并对两种组合结构的梁柱框架结构进行对比分析.
在本文中工字钢梁的钢材采用简化的两段线模型,适用于低碳钢,弹性模量为206 GPa,泊松比为0.262,其双直线模型如图1所示.

图1双直线模型
Fig.1Doublelinearmodel
核心区混凝土受到方钢管柱的约束,其塑性能力得到提高,故普通混凝土单轴应力应变曲线无法反映出核心混凝土塑性性能的提升.为了充分考虑方钢管柱对核心区混凝土的约束效应,本文采用刘威[5]提出的核心区混凝土本构模型,如图2所示.刘威在谭清华等[6]提出的混凝土本构模型的基础上对其峰值和下降段进行了修改,使其更加适用于有限元分析,其应力应变关系的函数表达式为
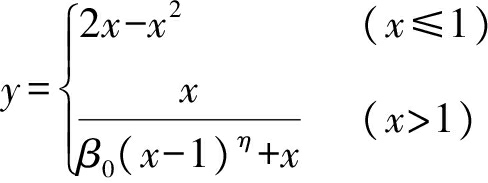
(1)
式中:x=ε/ε0,ε0=εc+800×10-6ξ0.2,ξ为截面的约束效应系数,ξ=asf/fc,as为构件的截面含钢率,fc为混凝土轴心抗压强度设计值,εc=10-6(1 300+12.5fc);y=σ/σ0,σ0=fc;η=1.6+1.5/x;β0=![]() ).
).
单层单跨方钢管混凝土柱![]() 工字钢梁框架模型采用文献[4]中实际试验数据120 mm×120 mm×3.46 mm方钢管柱和160 mm×80 mm×3.44 mm×3.44 mm(梁高、梁宽、腹板厚度、翼缘厚度)工字钢梁.工字钢梁和外加强环通过焊接连接在方钢管柱上,模型中采用绑定连接.方钢管柱、工字钢梁和加强环板模型采用S4R壳单元,核心混凝土采用C3D8R实体单元建模.定义混凝土和方钢管之间的接触单元[7]时,应该考虑其切向行为和法向行为,切向行为采取罚摩擦公式,摩擦系数为0.6;法向行为定义为“硬”接触.一榀方钢管混凝土框架模型尺寸如图3所示(单位:mm).有限元软件建立的框架模型及单元划分模型如图4所示.
工字钢梁框架模型采用文献[4]中实际试验数据120 mm×120 mm×3.46 mm方钢管柱和160 mm×80 mm×3.44 mm×3.44 mm(梁高、梁宽、腹板厚度、翼缘厚度)工字钢梁.工字钢梁和外加强环通过焊接连接在方钢管柱上,模型中采用绑定连接.方钢管柱、工字钢梁和加强环板模型采用S4R壳单元,核心混凝土采用C3D8R实体单元建模.定义混凝土和方钢管之间的接触单元[7]时,应该考虑其切向行为和法向行为,切向行为采取罚摩擦公式,摩擦系数为0.6;法向行为定义为“硬”接触.一榀方钢管混凝土框架模型尺寸如图3所示(单位:mm).有限元软件建立的框架模型及单元划分模型如图4所示.
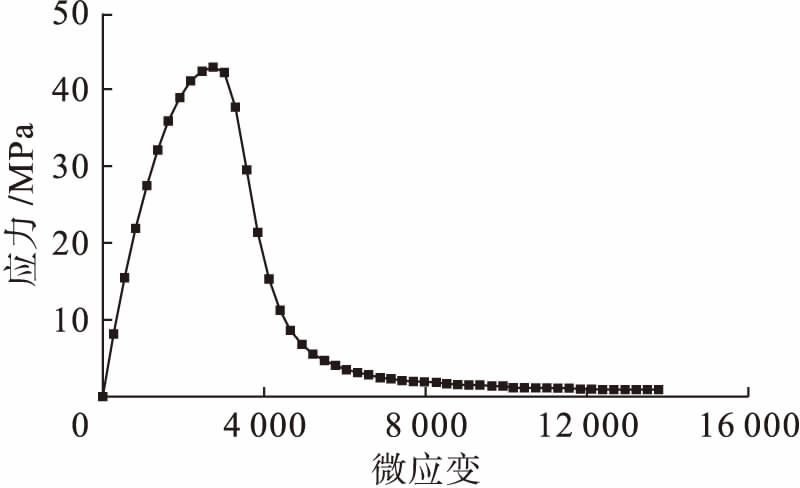
图2核心约束混凝土应力![]() 应变曲线
应变曲线
Fig.2Stress-straincurveofcoreconfinedconcrete
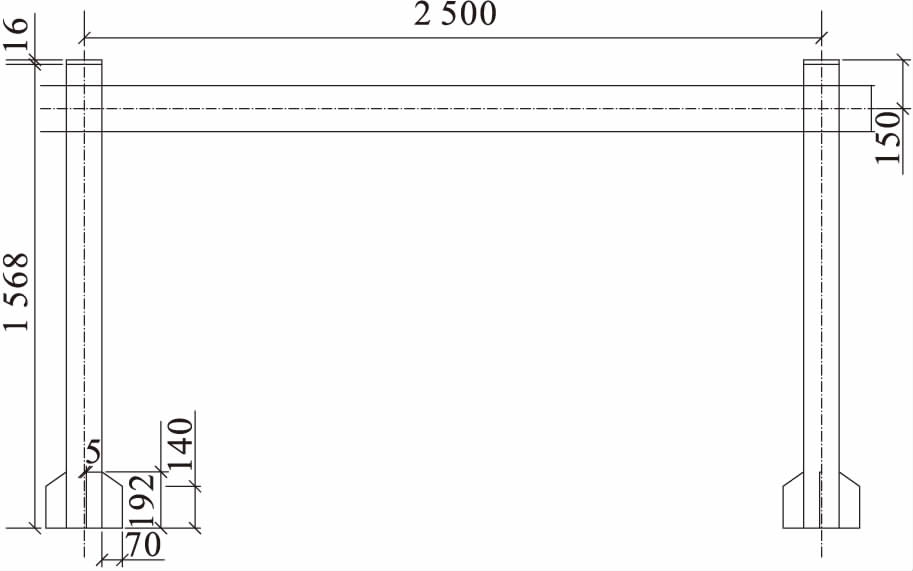
图3方钢管混凝土柱![]() 钢梁框架模型尺寸
钢梁框架模型尺寸
Fig.3Modeldimensionsofconcretefilledsquaresteeltubecolumn-Ibeamframe
本文中钢管混凝土框架试验边界条件和荷载的施加形式明确,柱脚固接,两柱顶施加轴向荷载,工字钢梁端右侧施加水平循环荷载.在有限元计算模拟中,对方钢管柱脚采取嵌固的边界条件,加劲板底部同样采用嵌固边界,由于只有柱顶板和底板限制了核心混凝土的轴向位移,所以核心混凝土的边界仅需约束其轴向位移即可.在荷载施加的过程中,梁端右侧水平循环荷载的加载过程采用位移加载控制,加载历程如图5所示,其中,Δ/Δy为试验过程中模型的位移值与模型屈服位移的比值.
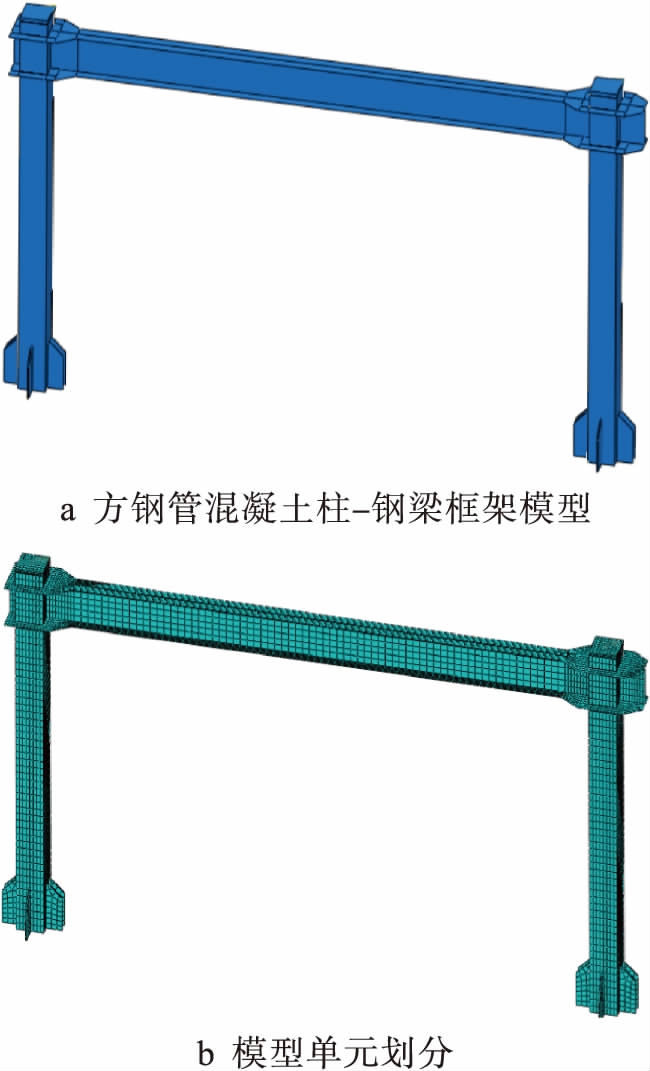
图4方钢管混凝土柱![]() 钢梁框架模型及模型单元划分
钢梁框架模型及模型单元划分
Fig.4Modelandmodelunitdivisionforconcretefilledsquaresteeltubecolumn-Ibeamframe
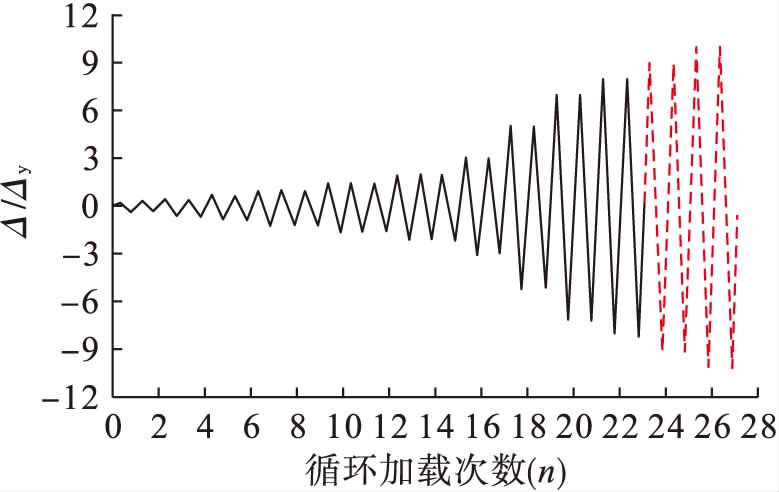
图5加载历程
Fig.5Loadinghistory
对于方钢管混凝土柱![]() 工字钢梁框架模型有限元计算和试验得到的荷载
工字钢梁框架模型有限元计算和试验得到的荷载![]() 位移滞回曲线如图6所示.
位移滞回曲线如图6所示.
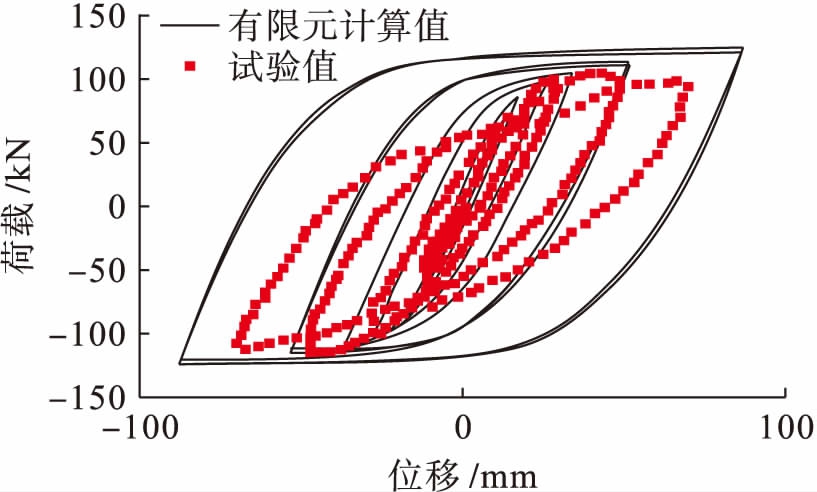
图6有限元计算和试验滞回曲线
Fig.6Hysteresisloopsfromfiniteelementcalculationandexperiment
通过滞回曲线得到的骨架曲线如图7所示.
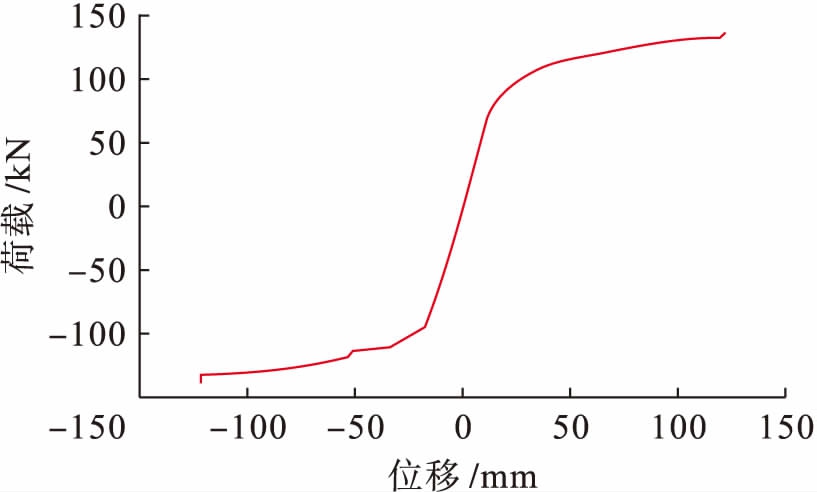
图7数值模拟所得骨架曲线
Fig.7Skeletoncurveobtainedfromnumericalsimulation
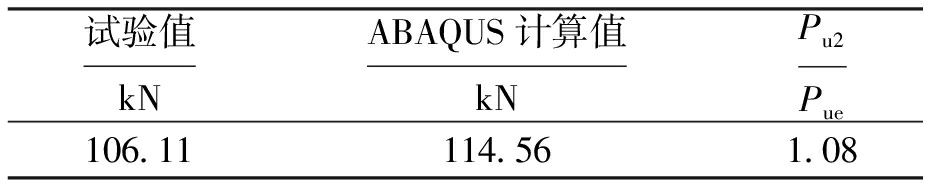
本文参考文献[8]中确定钢管混凝土柱屈服点的方法,根据骨架曲线来确定框架结构水平承载力.试件水平承载力计算结果与试验结果的比较如表1所示,其中,Pu2/Pue为钢管混凝土模型极限水平荷载模拟值与试验值的比值.
表1水平承载力计算结果与试验结果的比较
Tab.1Comparisonbetweencalculatedandexperimentalresultsofhorizontalbearingcapacity
模拟计算得到的滞回曲线为较饱满的梭形形状,表明整个框架结构具有很强的塑性变形性能和抗震耗能能力.有限元分析得出的模型整体刚度、水平极限承载力均大于试验结果,滞回环也相较试验结果更加饱满.分析表明,有限元模拟与试验值基本接近,总体上稍微偏大是由于有限元计算分析中未模拟结构的初始缺陷、安装过程中产生的误差等因素的影响.对比结果显示,运用有限元模拟的方法可以较好地对方钢管混凝土柱![]() 工字钢梁平面框架进行数值模拟分析.
工字钢梁平面框架进行数值模拟分析.
当遭遇地震荷载作用时,可采用结构吸收能量和耗散能量的多少作为评价结构抗震性能优劣的依据.滞回曲线的荷载![]() 位移加载段曲线围成的面积为整体结构吸收的能量.同理,荷载
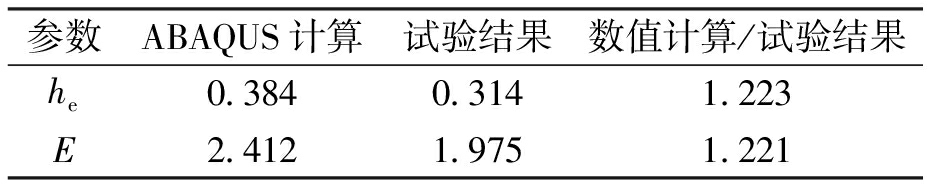
位移加载段曲线围成的面积为整体结构吸收的能量.同理,荷载![]() 位移卸载段曲线与加载曲线围成的面积为结构耗散的能量.本文利用等效粘滞阻尼系数he和能量耗散系数E当做评价结构耗能能力的参考指标,等效粘滞阻尼系数越大,说明结构的耗能能力越强[9].表2为有限元计算和试验得到的等效粘滞阻尼系数与能量耗散系数的对比.有限元模拟没有考虑钢材在循环荷载作用下的塑性损伤引起的刚度退化,从而使有限元计算出的等效粘滞阻尼系数和能量耗散系数均略大于试验结果.
位移卸载段曲线与加载曲线围成的面积为结构耗散的能量.本文利用等效粘滞阻尼系数he和能量耗散系数E当做评价结构耗能能力的参考指标,等效粘滞阻尼系数越大,说明结构的耗能能力越强[9].表2为有限元计算和试验得到的等效粘滞阻尼系数与能量耗散系数的对比.有限元模拟没有考虑钢材在循环荷载作用下的塑性损伤引起的刚度退化,从而使有限元计算出的等效粘滞阻尼系数和能量耗散系数均略大于试验结果.
表2粘滞阻尼系数和能量耗散系数对比
Tab.2Comparisonbetweenviscousdampingcoefficientandenergydissipationfactors
分析表明,方钢管混凝土柱![]() 工字钢梁框架模型有限元计算分析结果与实测试验数据总体吻合较好.采用所建立的有限元计算模型能够简便、快捷、准确地分析实际受力情况.
工字钢梁框架模型有限元计算分析结果与实测试验数据总体吻合较好.采用所建立的有限元计算模型能够简便、快捷、准确地分析实际受力情况.
为进一步探明钢管柱内填充混凝土后的作用,本文建立了空钢管柱![]() 工字钢梁框架模型,并对其进行有限元计算分析.将两种框架结构的计算结果进行对比分析,从而评价两种框架结构力学性能的优劣[10].
工字钢梁框架模型,并对其进行有限元计算分析.将两种框架结构的计算结果进行对比分析,从而评价两种框架结构力学性能的优劣[10].
通过统一钢管混凝土柱和空钢管柱的轴压承载力,从而计算出空钢管柱的厚度为7.3 mm.方空钢管柱![]() 工字钢梁框架模型其他尺寸与方钢管混凝土柱
工字钢梁框架模型其他尺寸与方钢管混凝土柱![]() 工字钢梁框架结构模型相同.
工字钢梁框架结构模型相同.
方钢管混凝土柱![]() 工字钢梁和方空钢管柱
工字钢梁和方空钢管柱![]() 工字钢梁框架结构统一计算到5Δy时对应的应力云图如图8所示.
工字钢梁框架结构统一计算到5Δy时对应的应力云图如图8所示.
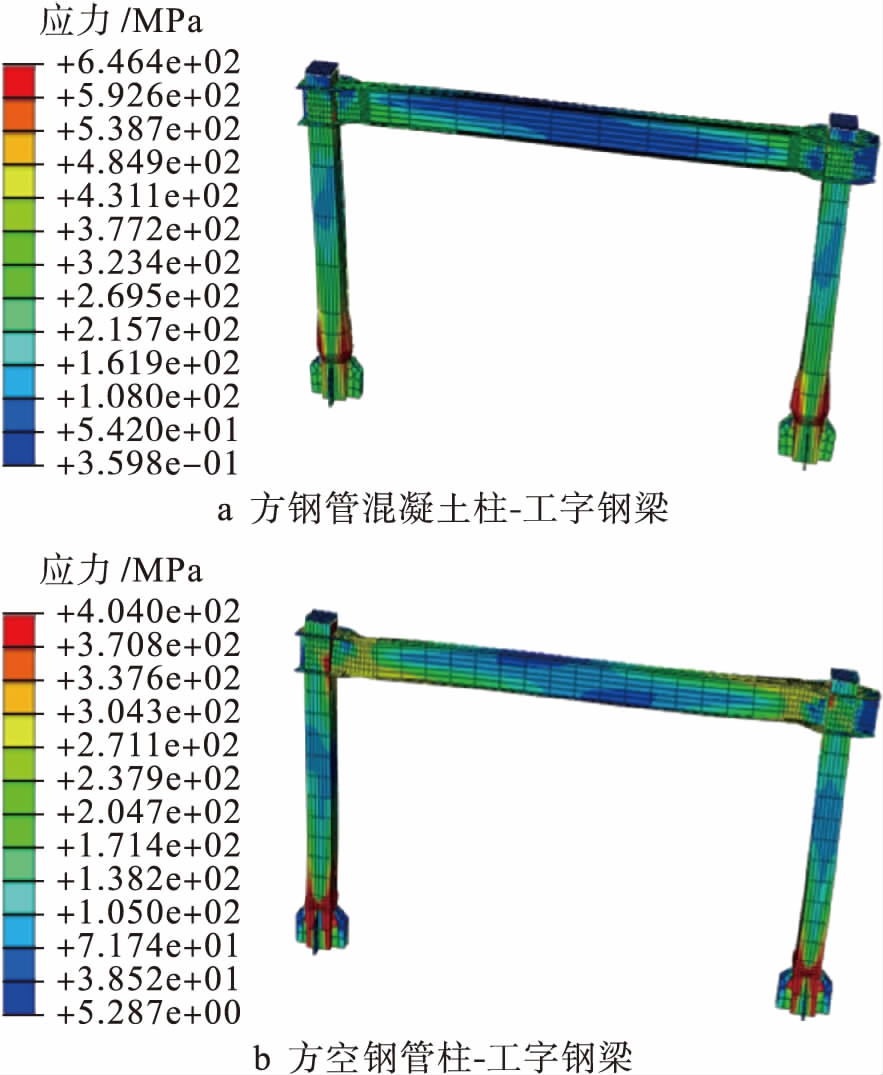
图8两种框架结构的应力云图
Fig.8Stressnephogramsoftwoframestructures
框架结构在受力过程中,首先在靠近梁端加载端的位置形成塑性铰,由于节点区存在加强环板,翼缘屈服区域分布在加强环板之外的钢梁截面上,工字钢梁左端上翼缘与右端下翼缘表面在压应力作用下率先进入塑性状态.方钢管柱脚钢管的屈服略晚于梁端,随着梁端屈服区域的变大,钢管柱脚仅有小部分进入塑性状态.在之后的加载过程中,梁端进入全截面屈服,首先形成塑性铰,并随着水平循环位移的继续增加,柱脚处钢管向外鼓曲,形成塑性铰,框架结构丧失承载能力,发生破坏,结构整体未出现明显的失稳现象.而方空钢管柱柱脚首先因失稳发生破坏,结构整体失稳现象明显.上述框架破坏模式说明,方钢管混凝土柱![]() 工字钢梁和方空钢管柱
工字钢梁和方空钢管柱![]() 工字钢梁框架采用外加强环板连接的节点形式满足“强柱弱梁”的抗震设防要求,形成了理想的“梁铰”破坏机制.
工字钢梁框架采用外加强环板连接的节点形式满足“强柱弱梁”的抗震设防要求,形成了理想的“梁铰”破坏机制.
由图8可知,塑性铰只出现在工字钢梁端部环板外侧和柱脚加劲板上方,而节点区钢管柱壁在加载过程中始终处于弹性阶段,表明采用外加强环连接节点的两种框架结构均满足“强节点、弱构件”的抗震设防要求.
图9为两种框架结构荷载![]() 位移曲线.由图9可知,两种组合结构的滞回曲线都呈饱满的梭形,说明两种结构的塑性变形能力很强,具有良好的抗震耗能能力.相比之下,钢管混凝土柱框架结构的滞回曲线更加圆滑、饱满.在框架结构的受力过程当中,受到方钢管柱约束其轴向位移的混凝土处于三向受压状态,从而提高了混凝土的受压承载力.正因为混凝土的存在,延缓了方钢管柱的局部屈曲变形,进一步提高了钢管混凝土柱的承载力.
位移曲线.由图9可知,两种组合结构的滞回曲线都呈饱满的梭形,说明两种结构的塑性变形能力很强,具有良好的抗震耗能能力.相比之下,钢管混凝土柱框架结构的滞回曲线更加圆滑、饱满.在框架结构的受力过程当中,受到方钢管柱约束其轴向位移的混凝土处于三向受压状态,从而提高了混凝土的受压承载力.正因为混凝土的存在,延缓了方钢管柱的局部屈曲变形,进一步提高了钢管混凝土柱的承载力.
骨架曲线为每个循环加载过程中荷载峰值点的连线,因此,骨架曲线能够反映出结构在每个循环过程中荷载![]() 变形对应的关系,同时有助于研究结构的抗震性能.骨架曲线能清楚地反映出结构承载力的多少,钢管混凝土柱框架结构的承载能力明显高于空钢管柱框架结构.两种框架结构的骨架曲线如图10所示.
变形对应的关系,同时有助于研究结构的抗震性能.骨架曲线能清楚地反映出结构承载力的多少,钢管混凝土柱框架结构的承载能力明显高于空钢管柱框架结构.两种框架结构的骨架曲线如图10所示.
为了更好地反映结构的强度退化,本文引用荷载强度退化系数![]() 其中,
其中,![]() 为第j级加载时,第i次循环峰值点的荷载值;
为第j级加载时,第i次循环峰值点的荷载值;![]() 为第j级加载时,第i-1次循环峰值点的荷载值.图11为两种框架结构的强度退化曲线.
为第j级加载时,第i-1次循环峰值点的荷载值.图11为两种框架结构的强度退化曲线.
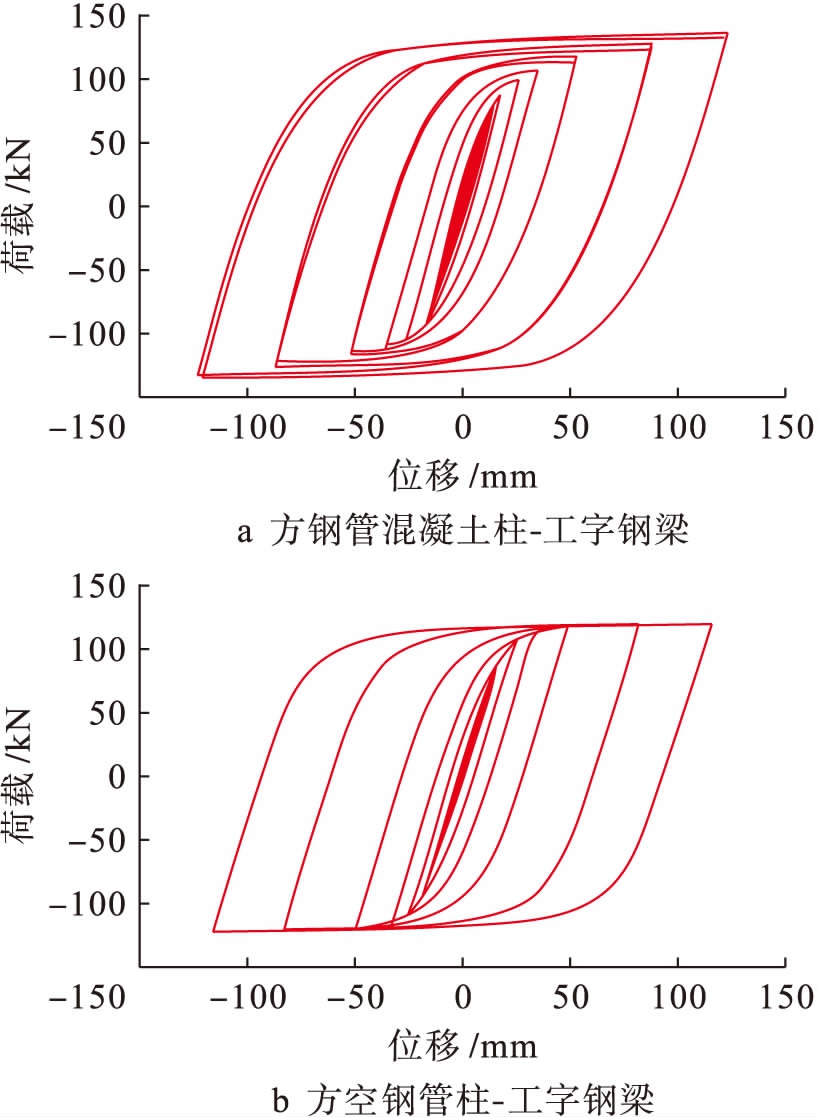
图9两种框架结构荷载![]() 位移曲线
位移曲线
Fig.9Load-displacementcurvesoftwoframestructures
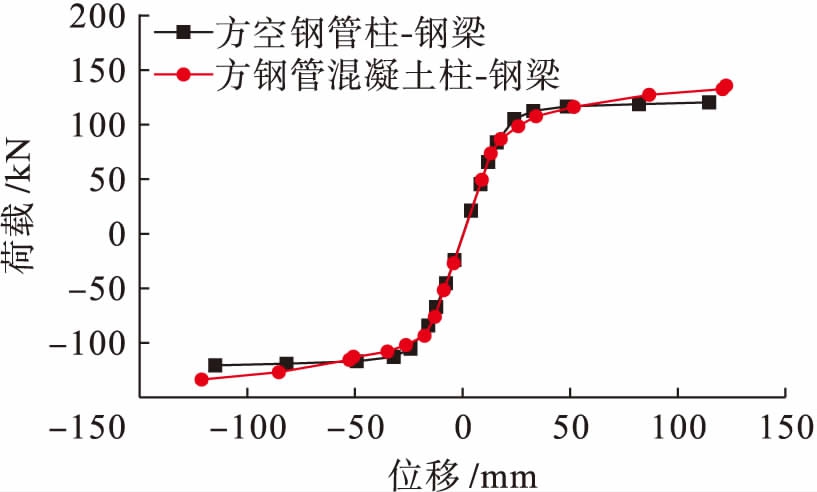
图10两种框架结构的骨架曲线
Fig.10Skeletoncurvesoftwoframestructures
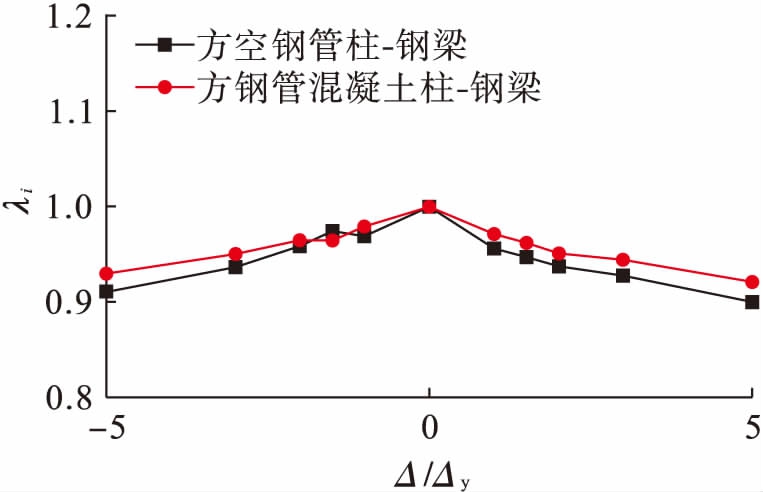
图11两种框架结构的强度退化曲线
Fig.11Strengthdegradationcurvesoftwoframestructures
刚度退化的定义参照《建筑抗震试验方法规程》(JGJ/T101-2015),同级变形下的割线刚度表达式为
![]()
(2)
式中:Ki为割线刚度;+pi,-pi为第i次正、反向峰值点的荷载值;+xi,-xi为第i次正、反向峰值点的位移值.
图12为两种框架结构的刚度退化曲线.图12中显示无混凝土的方空钢管柱![]() 工字钢梁框架结构的强度退化和刚度退化都更快一些.通过将钢材和混凝土两种材料组合在一起,不但克服了两者各自的缺点,而且还充分地发挥各自的优点,这也正是钢管混凝土结构的优势所在.
工字钢梁框架结构的强度退化和刚度退化都更快一些.通过将钢材和混凝土两种材料组合在一起,不但克服了两者各自的缺点,而且还充分地发挥各自的优点,这也正是钢管混凝土结构的优势所在.
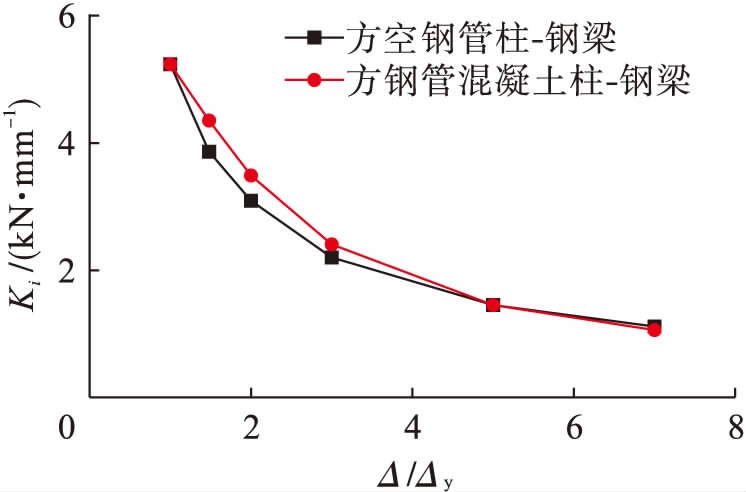
图12两种框架结构的刚度退化曲线
Fig.12Stiffnessdegradationcurvesoftwoframestructures
本文利用有限元软件ABAQUS建立了采用外加强环式节点连接形式的单层单跨方钢管混凝土柱![]() 工字钢梁及方空钢管柱
工字钢梁及方空钢管柱![]() 工字钢梁平面框架模型进行力学性能分析,并得出以下结论:
工字钢梁平面框架模型进行力学性能分析,并得出以下结论:
1) 数值模拟计算得到的方钢管混凝土柱![]() 工字钢梁框架模型的破坏模式、滞回曲线及承载力等数据均与试验结果吻合较好,表明建立的有限元计算模型能够较为准确、简便、快捷地模拟框架实际的受力情况.
工字钢梁框架模型的破坏模式、滞回曲线及承载力等数据均与试验结果吻合较好,表明建立的有限元计算模型能够较为准确、简便、快捷地模拟框架实际的受力情况.
2) 两种框架结构力学性能对比分析表明,方钢管混凝土柱![]() 工字钢梁框架结构在承载能力、耗能能力、强度刚度退化方面均优于方空钢管柱
工字钢梁框架结构在承载能力、耗能能力、强度刚度退化方面均优于方空钢管柱![]() 工字钢梁框架结构.
工字钢梁框架结构.
3) 有限元模拟分析得到的两种框架结构的滞回曲线、骨架曲线均未出现明显的下降段,这是由于试验中的最终破坏为方钢管柱脚的焊缝开裂导致框架结构的承载力降低.而在有限元计算分析中,方钢管柱作为一整体建立模型,忽略了钢材焊缝的缺陷,故未产生试验分析中明显的下降段曲线.
参考文献(References):
[1] 刘林林,屠永清,叶英华.基于ABAQUS的钢管混凝土L形柱有限元分析 [J].沈阳工业大学学报,2011,33(3):349-354.
(LIU Lin-lin,TU Yong-qing,YE Ying-hua.Finite element analysis of L-shaped concrete filled steel tubular column based on ABAQUS [J].Journal of Shenyang University of Technology,2011,33(3):349-354.)
[2] 龚永智,倪鸣,丁发兴,等.型钢![]() 方钢管混凝土轴压短柱力学性能有限元分析 [J].建筑结构学报,2014,35(增刊2):120-124.
方钢管混凝土轴压短柱力学性能有限元分析 [J].建筑结构学报,2014,35(增刊2):120-124.
(GONG Yong-zhi,NI Ming,DING Fa-xing,et al.Behavior of axially loaded steel-reinforced concrete-filled square stell tubular stub columns [J].Journal of Building Structures,2014,35(Sup2):120-124.)
[3] 黄远,朱正庚,张锐,等.端部栓钉加强方钢管混凝土柱非线性有限元分析 [J].建筑结构学报,2014,35(增刊2):137-144.
(HUANG Yuan,ZHU Zheng-geng,ZHANG Rui,et al.Nonlinear FEA of square concrete-filled steel tubular solumn strengthened with end studs [J].Journal of Building Structures,2014,35(Sup2):137-144.)
[4] 王文达.钢管混凝土柱![]() 钢梁平面框架的力学性能研究 [D].福州:福州大学,2006.
钢梁平面框架的力学性能研究 [D].福州:福州大学,2006.
(WANG Wen-da.Study on mechanical properties of concrete filled steel tubular column and steel beam plane frame [D].Fuzhou:Fuzhou University,2006.)
[5] 刘威.钢管混凝土局部受压时的工作机理研究 [D].福州:福州大学,2005.
(LIU Wei.Study on working mechanism of concrete filled steel tube under local compression [D].Fuzhou:Fuzhou University,2005.)
[6] 谭清华,韩林海.火灾后和加固后型钢混凝土柱的力学性能分析 [J].清华大学学报(自然科学版),2013,53(1):12-17.
(TAN Qing-hua,HAN Lin-hai.Post-fire and post-strengthening analysis of steel reinforced concrete co-lumns subjected to fire [J].Journal of Tsinghua Uni-versity (Science and Technology),2013,53(1):12-17.)
[7] 庄茁.基于ABAQUS的有限元分析和应用 [M].北京:清华大学出版社,2009.
(ZHUANG Zhuo.Based on ABAQUS finite element analysis and application [M].Beijing:Tsinghua University Press,2009.)
[8] 韩林海.钢管混凝土结构 [M].北京:科学出版社,2016.
(HAN Lin-hai.Steel tube concrete structure [M].Beijing:Science Press,2016.)
[9] 中华人民共和国住房和城乡建设部.JGJ/T101-2015建筑抗震试验方法规程 [S].北京:中国建筑工业出版社,2016.
(Ministry of Housing and Urban-Rural Development of the People’s Republic of China.JGJ/T101-2015 Specification for seismic test of buildings [S].Beijing:China Building Industry Press,2016.)
[10]王静峰,张琳,戴阳.半刚性钢管混凝土框架梁柱端板连接抗震性能试验研究 [J].土木工程学报,2012,45(11):13-21.
(WANG Jing-feng,ZHANG Lin,DAI Yang.Seismic experimental study of end plate connections for semi-rigid concrete-filled steel tubular frames [J].China Civil Engineering Journal,2012,45(11):13-21.)
WANG Ying, YI Kun
(School of Architecture and Civil Engineering, Shenyang University of Technology, Shenyang 110870, China)
Abstract:In order to compare and analyze the mechanical properties of two frame structures including both concrete filled square steel tube column-I beam and hollow square steel tube column-I beam frame structures, the full-scale modeling the above-mentioned two frame structures were carried out with the finite element software, and the nonlinear finite element calculation and analysis were completed.The results show that the calculated results agree well with the experimental data, which verifies the reliability of the established model.In addition, the hysteretic curves of two frame structures are in plump spindle-shape without obvious pinch phenomenon.Furthermore, the horizontal ultimate bearing capacity at the beam ends of concrete filled square steel tube column-I beam frame structure is higher than that of hollow square steel tube column-I beam frame structure.
Key words:concrete filled steel tube column; hollow steel tube column; frame; I-beam; external strong ring; joint; finite element; mechanical property
收稿日期:2016-06-28.
基金项目:日本高校合作基金资助项目(201367025).
作者简介:王 颖(1975-),女,辽宁丹东人,副教授,博士,主要从事钢混组合结构和工程抗震防灾等方面的研究.
* 本文已于2017-10-25 21∶13在中国知网优先数字出版.网络出版地址:http://kns.cnki.net/kcms/detail/21.1189.T.20171025.2113.036.html
doi:10.7688/j.issn.1000-1646.2018.01.21
中图分类号:TU 398.9
文献标志码:A
文章编号:1000-1646(2018)01-0115-06
(责任编辑:钟 媛 英文审校:尹淑英)