路径规划是机器人学的基本问题,其目的是在构型空间中求解一个特定序列,使得机器人自起点开始,避开不可达和存在碰撞风险的构型,最终到达目标构型[1].国内外大量学者均积极对其展开研究,同时提出了很多的规划策略与相关计算方法,例如遗传算法、蚁群算法、神经网络算法等都是常用的计算方法,这些方法对具有一定代价要求的路径规划都能够在某种程度上完成.
栅格法[2]是机器人对环境建模的主要方法之一,以栅格路径规划为基础的算法在目前有很多,例如A*、D*[3]、D*Lite[4]、FocussedD*[5]及其他方法.其中,D*、D*Lite、FocussedD*侧重于对环境动态变化引起的行驶代价变化问题的处理;而在已知的静态环境下,A*算法可以对两点间最短路径[6]快速计算.
但是基于栅格的A*路径规划算法存在一个问题,其立足于栅格的中心点,在状态空间中作为节点是能够被搜索的,也就是说它能够对8个邻域搜索,但路径搜索方向就会产生限定,即均属于π/4的整数倍.这样求解最终产生的路径实际上不是最优的,就路径长度而言也并非属于最短的,存在大量的转弯及大量的折点[7-8].
结合A*路径规划算法的缺点,本文对传统A*算法的搜索邻域进行了扩展,即从原来离散的8个增加为现在的24个,搜索方向也有了一定的改变,由限定方向转变为连续任意方向.改进的A*算法成功缩短了路径长度,减小了折点个数,实验证明该方法能够在栅格地图上求解出更优的路径,移动机器人路径规划具有了更高效率.
1 A*算法移动机器人路径规划
1.1 A*算法
A*算法[9]从本质而言,属于人工智能范畴,具有鲜明启发式搜索特征,算法因为其强大的灵活性以及对不同路况的适应能力,在路径规划搜索中受青睐.A*算法最为成功的特点体现为:它将Dijkstra算法(靠近初始点的节点)和BFS算法(靠近目标点的节点)的信息块结合起来,将从初始节点到任意节点n的代价g(n)与从节点n到目标点的启发式评估代价h(n)结合起来,评价当前节点,其评价函数为
f(n)=g(n)+h(n)
式中:f(n)为从初始点经由节点n到目标点的估价函数;g(n)为状态空间中从初始节点到n节点的实际代价;h(n)为当前节点n至目标节点路径这一过程中的预算代价,它在评价函数中起关键性作用,决定了A*算法效率的高低.
A*算法结合具体路径规划要达到的目的,设计与之相适应的启发函数,从而使搜索方向越来越接近目标状态.
A*算法原理图如图1所示,包含开始节点(start)、障碍物、结束节点(end),需要通过A*算法规划从start节点到end节点的路线.探寻过程中,会以当前节点为基点,扫描其相邻的八个节点,计算当前节点与start节点及到end的距离,从而计算出最短路径.
以start节点为例,探寻相邻的八个节点,且只能上下左右移动,每移动到邻近的单元格,就认为行走了一个距离.如从start移动到A节点,移动了两个距离,当从A节点移动到end节点(此时忽略障碍,仅计算距离)时,g(n)即可以理解为g(A)=2,h(n)可理解为h(A)=6,f(n)即为start节点到end节点的实际距离,公式描述为f(A)=g(A)+h(A)=8.于是便有了A节点的数字描述:f(n)位于左上方,g(n)位于左下方,h(n)位于右下方.同理可计算出f(B)=g(B)+h(B)=1+5=6.将start相邻的其它节点距离都计算出来,便可以通过对相邻节点的遍历及父节点的不断嵌套来形成一条路径.如把start相邻的所有节点进行遍历比较,选出f(n)最小的一个节点(称为X节点),并设置X节点的父节点为start节点,以X节点为当前节点,再判断X节点周围的有效节点(非障碍物点),选出f(n)最小的节点后设置X节点为其父节点,依次类推,就形成了一条节点线.
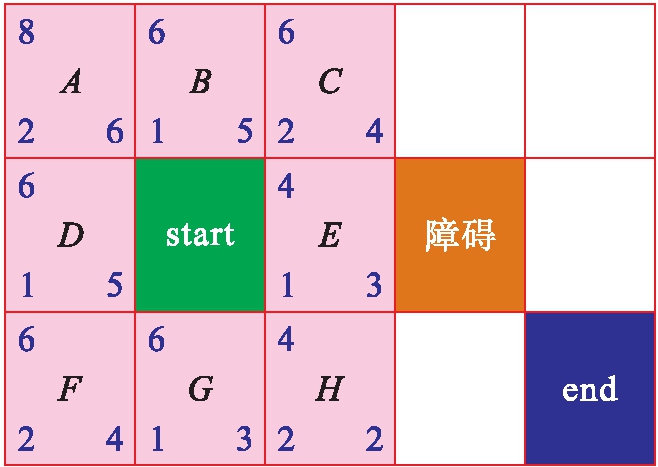
图1 A*算法原理示意图
Fig.1 Schematic A*algorithm principle
1.2 路径规划算法
A*算法在执行路径规划时主要用两个表来实现节点的扩展和最优节点的选取:OPEN表和CLOSE表.OPEN表作用是保存搜索过程中遇到的扩展节点,同时将这些节点按代价值进行排序;CLOSE表作用是保存OPEN表中代价值最小的可扩展节点.
本文将A*算法应用在栅格地图上进行路径规划,启发式信息h(n)为当前节点(xn,yn)和目标节点(xT,yT)之间的直线距离,即
A*算法移动机器人路径规划过程如下:
1) 在OPEN表纳入起点,CLOSE表纳入障碍点.
2) 选取OPEN表中具有最小f值的节点n,将其纳入CLOSE表.
3) 判断n是否为目标点,若n是目标点,则根据它的前向指针生成最优路径;若n不是目标点,则扩展节点n,生成后继节点m.
4) 在OPEN表中建立从后继节点m返回到n的指针,计算f(m)=g(m)+h(m).
5) 增加判断语句来判断OPEN表中是否已有节点m,如果判断失败,就应在OPEN表纳入m;若判断成功,则比较拥有不同前向指针的f(m)值的大小,选取较小的f(m)值.
6) 更新g(m),f(m)以及后继节点m的前向指针.
7) 按照数值大小的正序排列,把f值在OPEN表中进行重新排序,并返回步骤2).
路径规划的流程图如图2所示.
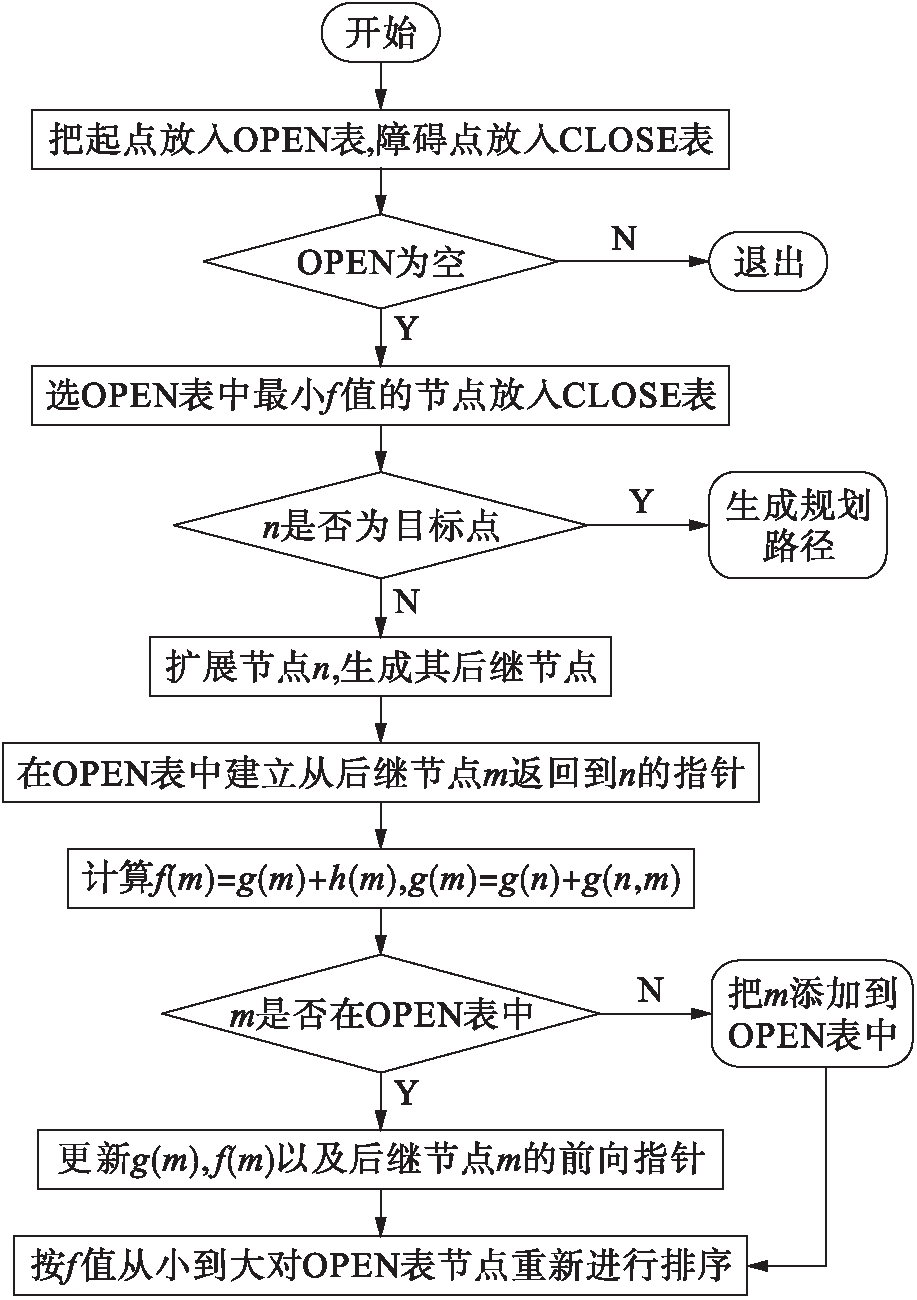
图2 移动机器人路径规划流程
Fig.2 Flow chart of path planning of mobile robot
2 改进A*算法
2.1 24邻域扩展
传统A*算法的8邻域示例图如图3所示.在栅格地图上使用A*算法进行路径规划时,每个栅格的中心都被假设为节点[10],节点临近的8个区域都是这个节点的扩展个数,因此运动方向的角度也被限定为π/4的整数倍.传统A*算法规划路径如图4所示,图4中虚线为根据传统A*算法所得到的自动最佳路径,路径有转折点,比较复杂,并非起终点之间的最佳期望路径.
为获得更好的规划路径,本文对原有的A*算法进行了改进.将传统A*算法的每个节点扩展邻域由8个增至24个.扩展算法的过程为:对于每个输入点的待扩展点,检查它四周的24个邻接点(x坐标-2~2,y坐标-2~2)可否加入扩展列表,判断邻接点是否还在网格图范围内.如果一个邻接点是内圈的点,只要检查邻接点本身是否为障碍点(是否在CLOSE表里面),若不是障碍点,则将此邻接点加入扩展列表中;如果一个邻接点是外圈的点,除了检查邻接点本身是否为障碍点外,还要检查输入点到邻接点路径中的1~2个点是否在CLOSE表里,再判断途经点是否在CLOSE表中,如果判断失败,则将相关的邻接点纳入到OPEN表中.
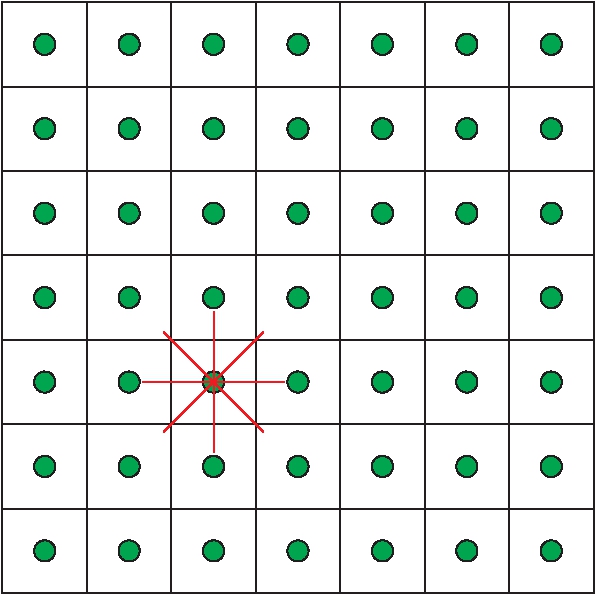
图3 传统A*算法8邻域示意图
Fig.3 Schematic 8 neighborhoods intraditional A*algorithm
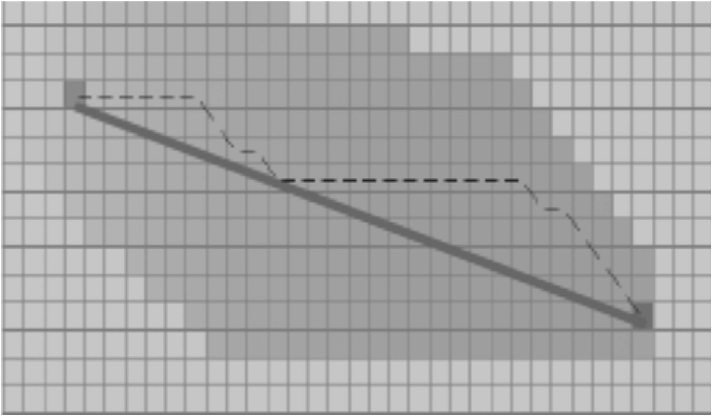
图4 传统A*算法规划路径
Fig.4 Path planning in traditional A*algorithm
2.2 改进A*算法路径规划
以A*算法对障碍物和移动路线进行预判计算,由于采用新的启发式信息因素,则在计算难度和相对复杂程度上要小很多,同时也提高了效率.另外,在启发式信息提供阶段,在前期的搜索中删除了一部分节点,而且存在实践性积累和计算经验等方面的困扰,这些节点的删除可能会对最终结果产生不良影响.为了防止产生次优解,在之前节点搜索邻域定义为24邻域基础上再进行改进:选取OPEN表中具有最小f值和次小f值的节点生成后继节点.改进A*算法路径规划过程如下:
1) 把源节点纳入OPEN表中,且作为唯一节点,同时对CLOSE表进行调整,该表初始情况下只存入障碍点的相关数值.
2) 依据新的扩展算法进行扩展.
3) 在OPEN表里将f值中最小的数值节点作为最佳的节点best1,然后选择次小的节点,并定义为best2,两个数值最佳的节点在扩展后由OPEN表移动到CLOSE表,用来预判best1是否为原定目标.如判断正确,即可转入步骤4);如判断错误,那么综合地图数据库里的道路与节点数据进行运算,从而对两个最佳节点进行扩展运算生成后继节点.
4) 逆向推理判断,从最佳节点回溯到原始节点,完成最终报告.
3 模拟实验
本文实验条件如下:CPUIntel Core2 Duo计算机,内存2 048 Mbit,所用编辑代码工具为Matlab 7.0.分别采用A*算法、24邻域A*算法和44邻域A*算法在栅格地图上进行5组不同距离长度的路径规划实验.表1列举了传统A*算法、24邻域A*算法、44邻域A*算法三种算法5组实验路径长度的数据对比;表2则列举了三种算法扩展点数与搜索时间情况;图5为传统A*算法与改进A*算法仿真路径对比的结果.
表1 规划路径长度对比
Tab.1 Comparison in length of planned pathm
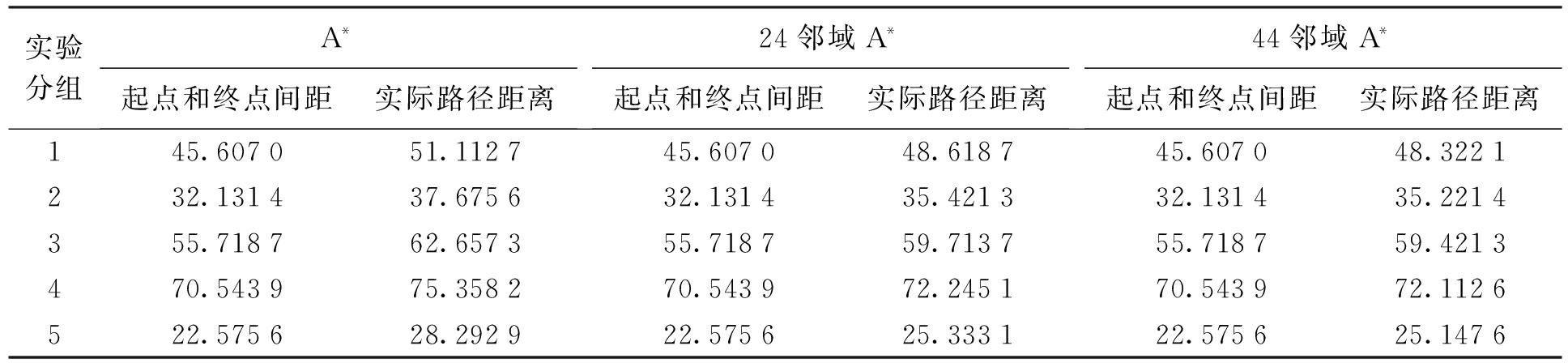
表2 扩展点数和搜索时间对比
Tab.2 Comparison in extension points and searching time
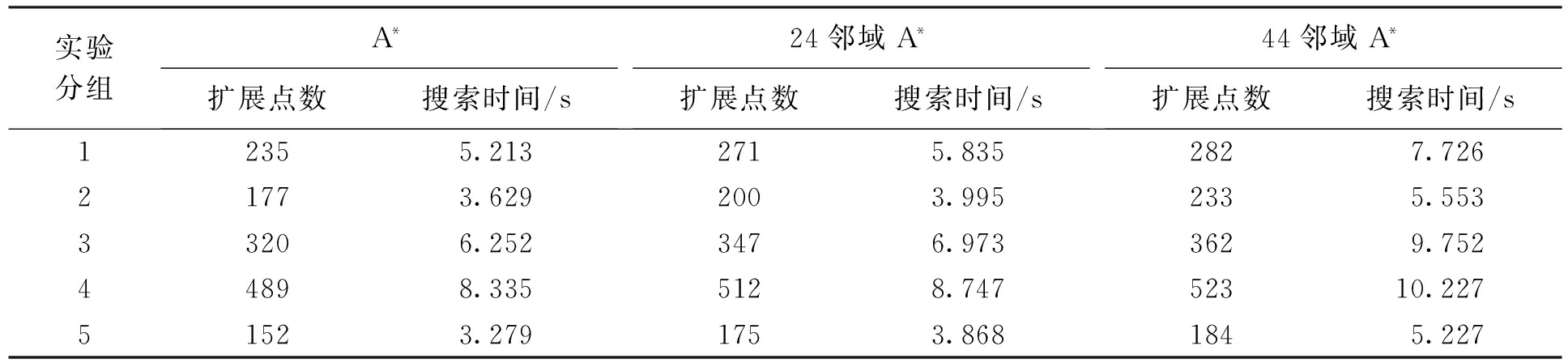
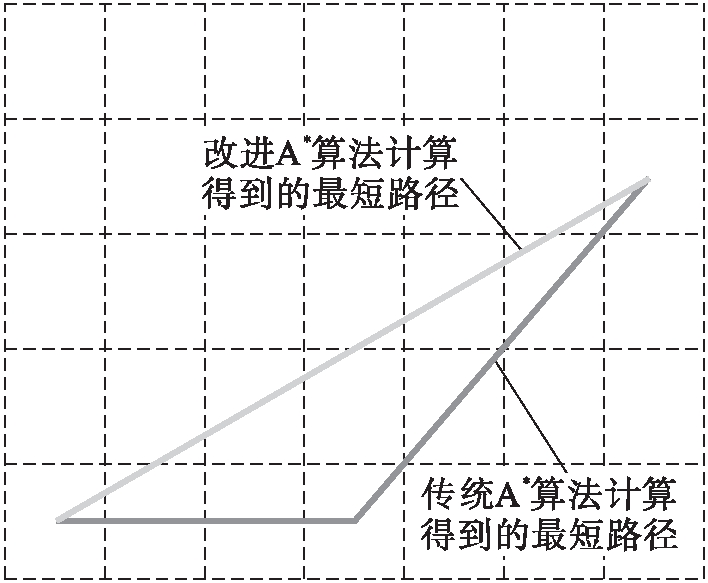
图5 传统A*和改进A*算法仿真路径对比
Fig.5 Comparison in simulated paths between traditionalA*and improved A*algorithms
模拟实验的数据表明:利用传统A*算法所得的最终结果存在转折多、线路复杂的问题,但这些问题在A*改进算法中得到了有效改进.对比表1、2数据可知,24邻域A*算法与44邻域A*算法在规划路径长度上相差无几,且均优于传统A*算法路径.但在规划时间上,44邻域搜索相较于24邻域搜索耗费了更长的时间.扩展点数上,改进A*算法相较于A*算法有所增多,避免了原算法最优节点过早删除.综上所述,24邻域A*算法路径规划的效率最高.
4 结 论
本文提出了改进A*算法,将可搜索邻域个数从离散的8个扩增为24个,因此,可移动方向也从π/4的整数倍变为连续更多的方向.同时采用了f最小值和次小值两点同时扩展,能够有效解决传统A*算法在栅格地图上进行路径规划时,求解得到的路径长度不是最优以及转折点较多的问题.在移动机器人路径规划中,相比于传统的A*算法,改进算法能规划出一条更优的可行驶路径,特别是对于栅格划分较为粗糙的栅格地图,优化程度更为明显.
参考文献(References):
[1] 张浩杰,龚建伟,姜岩,等.基于变为度状态空间的增量启发式路径规划方法研究 [J].自动化学报,2013,39(10):1602-1610.
(ZHANG Hao-jie,GONG Jian-wei,JIANG Yan,et al.Research on Incremental heuristic path planner with variable dimensional state space [J].Acta Automatic Sinica,2013,39(10):1602-1610.)
[2] 张继文,刘莉,陈恳.面向全方位双足步行跟随的路径规划 [J].自动化学报,2016,42(2):189-201.
(ZHANG Ji-wen,LIU Li,CHEN Ken.Omni-directional bipedal walking path planning [J].Acta Automatic Sinica,2016,42(2):189-201.)
[3] 张慧,荣学文,李贻斌,等.四足机器人地形识别与路径规划算法 [J].机器人,2015,37(5):547-551.
(ZHANG Hui,RONG Xue-wen,LI Yi-bin,et al.Terrain recognition and path planning for quadruped robot [J].Robot,2015,37(5):547-551.)
[4] 葛延峰,陈涛,孔祥勇,等.改进蚁群算法在城市汽车导航中的应用 [J].控制工程,2016,23(1):134-137.
(GE Yan-feng,CHEN Tao,KONG Xiang-yong,et al.Application of improved ant colony algorithm in car nevigation [J].Control Engineering of China,2016,23(1):134-137.)
[5] 陈长征,项宏伟,杨孔硕,等.可变形履带机器人跨越台阶的动力学分析 [J].沈阳工业大学学报,2015,37(2):166-170.
(CHEN Chang-zheng,XIANG Hong-wei,YANG Kong-shuo,et al.Dynamic analysis for variable tracked robot in process of climbing steps [J].Journal of Shenyang University of Technology,2015,37(2):166-170.)
[6] 吴宏超,刘检华,唐承统,等.基于改进A*算法的管路自动布局设计与优化方法 [J].计算机集成制造系统,2016,22(4):946-954.
(WU Hong-chao,LIU Jian-hua,TANG Cheng-tong,et al.Automatic pipe layout design and optimization method based on A* algorithm [J].Computer Integrated Manufacturing Systems,2016,22(4):946-954.)
[7] de Filippis L,Guglieri G,Quagliotti F.Path planning strategies for UAVS in 3D environments [J].Journal of Intelligent & Robotic Systems,2012(65):247-264.
[8] 王殿君.基于改进A*算法的室内移动机器人路径规划 [J].清华大学学报(自然科学版),2012,52(8):1085-1089.
(WANG Dian-jun.Indoor mobile-robot path planning based on an improved A* algorithm [J].Journal of Tsinghua University(Science and Technology),2012,52(8):1085-1089.)
[9] Pehlivaolu Y V.A new vibrational genetic algorit hm enhanced with a voronoi diagram for path planning of autonomous UAV [J].Aerospace Science and Technology,2012(16):47-55.
[10]Mei T,Liang H,Kong B,et al.Development of intel-ligent pioneer unmanned vehicle[C]//Intelligent Vehicles Symposium.Piscataway,USA,2012:938-943.