当前能源危机和环境污染问题日益凸显，新能源代替燃料缓和了能源与环境的矛盾[1-3]，因此，发展新能源汽车成为汽车行业的主要趋势.电动汽车是新能源汽车的主体，电池管理系统是电动汽车的重要组成部分，用于监视电池的状态.电池荷电状态(state of charge，SOC)作为电池管理系统最为关键的技术，反映电池的剩余电量，代表汽车的续航能力，因此，研究电池SOC估计问题对驾驶员掌握续航能力，及时补充电量具有重要意义.
电池SOC无法直接测量，只能通过测量电池其他状态量来间接测量.电池SOC估计的传统方法有放电实验法、按时积分法、开路电压法及内阻法等，放电实验法[4]精度较高，但只适用于实验室条件，无法应用于汽车行驶中；按时积分法[5]简单可靠，但对传感器精度依赖性较强，容易产生积累误差；开路电压法[6]只适用于电池稳定状态，但汽车行驶过程中电池状态突变较多；内阻法[7]在电池放电后期估计精度较好，但是内阻难以精确测量.电池SOC估计常用的智能算法包括神经网络算法和卡尔曼滤波，神经网络法[8]适用于所有电池，但是需要大量数据进行训练；卡尔曼滤波[9]对电池模型的精确性要求较高，电池突变时此算法的估计结果极差.
寻求一种能够时刻满足SOC精度要求的估计方法是当前研究的热点.本文针对卡尔曼滤波无法跟踪电池状态突变的情况，结合强跟踪原理提出了强跟踪卡尔曼滤波方法，在电池状态突变的情况下，此算法SOC的估计结果依然能够满足精度要求.
1 锂电池建模及参数辨识
1.1 锂电池建模
对锂电池进行建模要满足两个要求：一是能够准确模拟电池的动静态特性；二是模型不能过于复杂，以减少运算量.常见的锂电池等效电路模型包括理想模型、戴维南模型、PNGV模型及双阶RC模型等.理想模型只考虑电池内阻；戴维南模型比理想模型多出并联RC回路，模拟极化现象；PNGV模型在戴维南模型基础上串联了电容，反应动态过程；双阶RC模型将电池的电化学极化和浓差极化现象分开等效，其在三种模型中具有最高的等效精度.文献[10]已经证明，三阶RC模型相比于双阶RC模型精度变化不明显，但模型复杂度却显著提高，因此，本文选用双阶RC模型，其等效电路如图1所示.
图1中，Uoc等效为电池的开路电压；Ut等效为电池的端电压；R0等效为电池的欧姆内阻，用于反映电池的突变现象；RsCs回路等效电池的浓差极化，用于反映电池突变后的快速反应过程；RdCd回路等效电池的电化学极化，用于反映电池突变后的慢速反应过程；I为电池的内部电流.
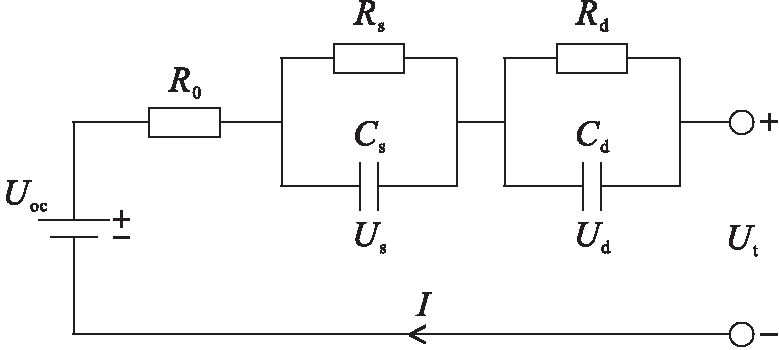
图1 双阶RC模型
Fig.1 Two-order RC model
记电池载荷状态为qSOC，Rs端电压为Us，Rd端电压为Ud，选择电池系统的状态量为x=[qSOC，Us，Ud]T，则双阶RC模型的状态方程为
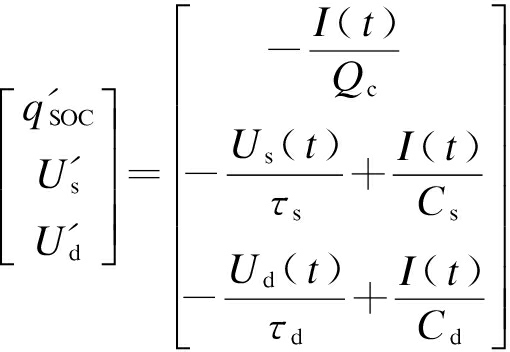
(1)
式中：Qc为电池荷载量；τs、τd分别为RsCs回路、RdCd回路的时间常数；初始参数为I(t0)=0 A，Us(t0)=0 V，Ud(t0)=0 V，Uoc=3.5 V.双阶RC模型的输出方程为
Ut(t)=Uoc-Us(t)-Ud(t)-R0I(t)
(2)
1.2 模型参数辨识
首先建立开路电压Uoc与荷电状态qSOC的对应关系，由于锂电池具有滞回电压特性，也就是其充电的开路电压大于放电的开路电压，因此，分别建立放电过程关系式与充电过程的关系式.以放电过程为例，在25 ℃恒温下将电池充满电至3.5 V后静置2 h，而后放电1 C，放电时间为5 min，静置5 min，将静置期间最大电压作为此荷电状态的开路电压，重复此过程直到电池电压小于2 V，此时电池放电完毕.
对实验所得数据进行多项式拟合，经拟合可知，7阶模型的拟合精度比6阶模型精度高一个数量级，但8阶模型与7阶模型精度相差较小，因此，本文使用7阶模型进行拟合，拟合曲线如图2所示.由图2可以看出，放电曲线与充电曲线差距相差较小，故选用其均值曲线作为最终结果，最终得到的均值曲线表达式为
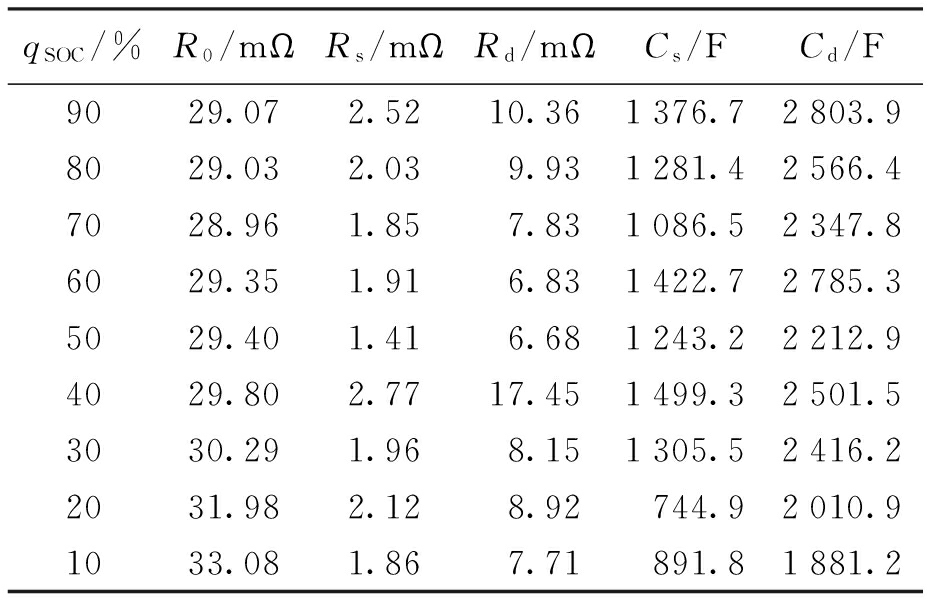
由图1可以看出，需要辨识的模型参数包括R0、Rs、Rd、Cs、Cd，由于电池在不同qSOC下模型参数值不同，因此，qSOC每间隔10%进行参数辨识.充电和放电时模型参数不一致，因此，需要对充电和放电过程分别进行辨识.本文使用HPPC测试方法[11]，具体测试方法为放电10 s，放电电流为3.7 A，而后静置40 s，再以2.8 A电流充电10 s.qSOC每间隔10%测试时，电池需静置30 min，测试结果如表1、2所示.由表1、2可知，该模型在不同的qSOC时需要不同模型参数，以保证近100%的精度.但考虑不同科学研究与工业测试具有一定的可容忍误差，为此可采用平均值作为模型参数实现通用性与可移植性.
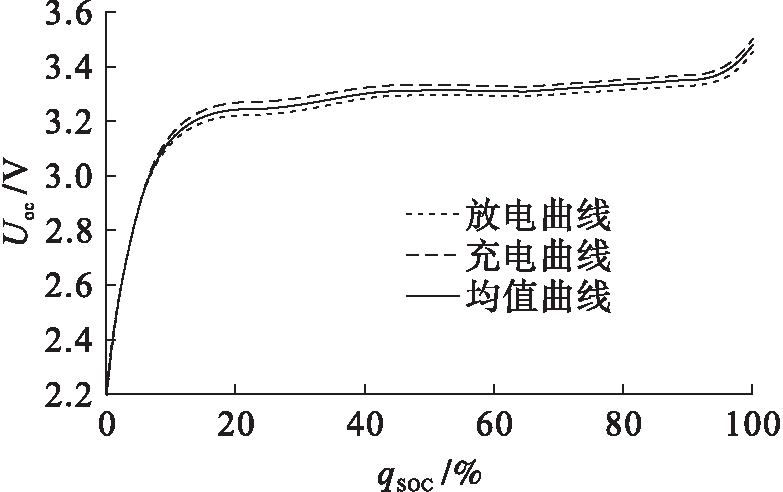
图2 Uoc-qSOC拟合曲线
Fig.2 Uoc-qSOC fitting curves
表1 放电过程模型参数
Tab.1 Model parameters for discharge process
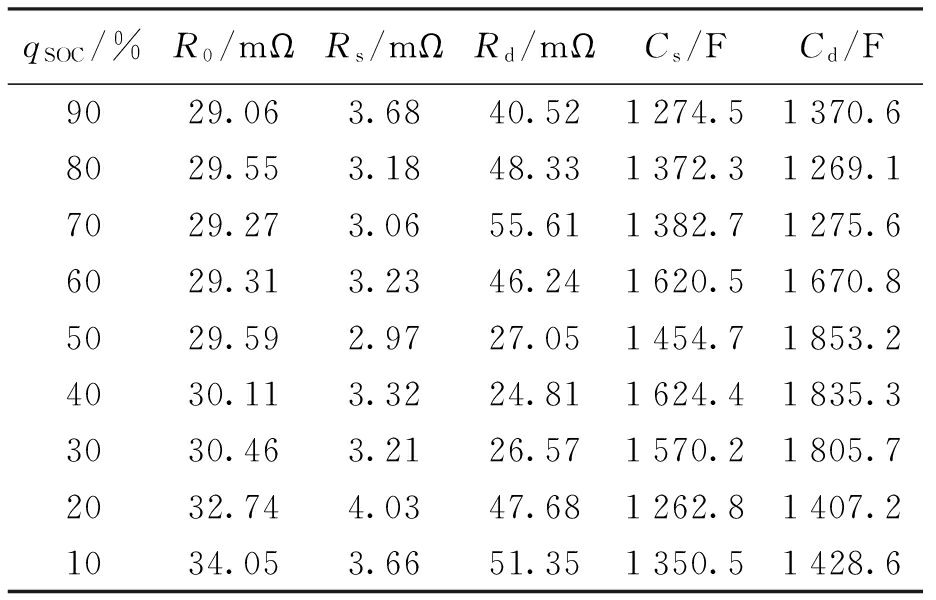
表2 充电过程模型参数
Tab.2 Model parameters for charging process
2 强跟踪卡尔曼滤波器
2.1 扩展卡尔曼滤波
标准卡尔曼滤波只适用于线性系统，但锂电池在使用过程中是严重的非线性系统，因此，本文使用扩展卡尔曼滤波[12-17]对锂电池系统状态进行估计.扩展卡尔曼滤波就是将非线性系统进行泰勒级数展开，保留其中的零次项和一次项，省略高次项，从而将非线性系统近似为线性系统.非线性系统的状态空间方程和观测方程为
(3)
式中：f(xk，uk)为状态转移函数；h(xk，uk)为观测函数；uk为系统非线性度；wk、vk为状态空间方程和观测方程的初始参量.将非线性函数f(xk，uk)、h(xk，uk)在
处进行泰勒展开，保留零次项和一次项得
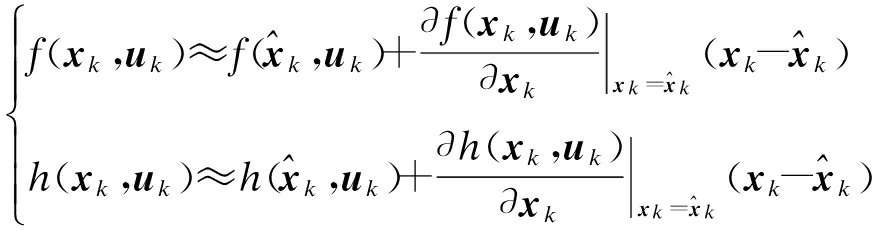
(4)
将表达式进行简化，记
则可将非线性系统式(3)线性化为
(5)
对线性系统式(5)使用卡尔曼滤波方程就实现了扩展卡尔曼滤波，具体实现过程中各表达式表述为：
1) 状态估计，
2) 误差协方差矩阵，Pk=Ak-1Pk-1Ak-1+Qk-1，其中，Qk-1为误差矩阵；
3) 卡尔曼修正矩阵，
其中，Rk为修正均值；
4) 系统状态更新，
5) 误差协方差阵更新，Pk+1=(I-LkCk)Pk.
按上述5个步骤进行反复迭代，便可实现系统状态的最优估计.
2.2 强跟踪卡尔曼滤波器设计
使用扩展卡尔曼滤波算法对锂电池系统状态进行估计存在以下问题：
1) 非线性系统进行线性化时会产生较大的近似误差；
2) 系统参数发生变化时，会产生系统模型不准确问题；
3) 系统在平稳状态下，卡尔曼增益矩阵会趋于较小值，而锂电池在使用过程中会发生状态突变，增益矩阵无法产生相应变化跟踪这一突变，从而产生较大估计误差.
为了解决这些问题，本文提出了强跟踪卡尔曼滤波算法，引入时变渐消因子，强行使残差序列保持正交，提高模型的鲁棒性，从而提升电池系统状态估计的精度.
对于式(3)所给的非线性系统，设计的强跟踪卡尔曼滤波器为
(6)
式中，
滤波器的强跟踪特性实现就是在线确定增益矩阵Lk.
为了实现滤波器的强跟踪特性，在确定增益矩阵Lk时，需要使其满足
(7)
式(7)的含义为：当模型不准确时，状态估计值与实际值差别较大，通过在线确定增益矩阵Lk，使式(7)成立，也就是使残差相互正交保持高斯特性，并时刻保持对系统的精确跟踪；若系统模型准确，式(7)就会自然成立，此时强跟踪卡尔曼滤波退化为扩展卡尔曼滤波.
2.3 强跟踪卡尔曼滤波实现
实现卡尔曼滤波算法的前跟踪特性，基本思想是通过引入渐消因子逐渐减小老数据对估计值的权重，对扩展卡尔曼滤波的误差协方差矩阵改进为
Pk=λkAk-1Pk-1Ak-1+Qk-1
(8)
式中，λk为时变渐消因子，且λk≥1.
使用式(7)给出的正交原理求解渐消因子时，需要使用梯度方法.此方法使用非线性规划求解最优渐消因子，计算量过大，无法实现在线计算，因此，文献[18]给出次优渐消因子的计算方法，即
(9)
式中，ek=tr(Nk)/tr(Mk).其中的Nk，Mk定义为
(10)
式中：V0，k为残差协方差阵，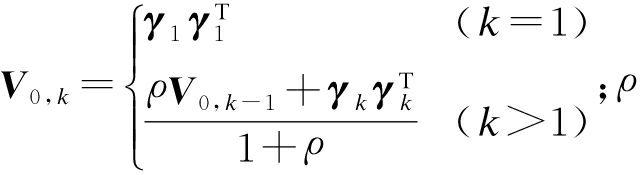
为遗忘因子；β为弱化因子，且β≥1.
结合式(1)、(2)给出的锂电池系统状态空间方程描述，得到离散化的状态空间模型为
(11)
式中：
Dk=diag(1，exp(-Δt/τs)，exp(-Δt/τd))
Bk= [-Δt/Qc，Rs(1-exp(-Δt/τs))，
Rs(1-exp(-Δt/τd))]T
基于以上分析，强跟踪卡尔曼滤波算法的电池qSOC估计具体表述为：
1) 状态估计，
2) 计算观测输出，
3) 误差协方差矩阵，Pk=λkAk-1Pk-1Ak-1+Qk-1；
4) 卡尔曼修正矩阵，
5) 系统状态更新，
6) 误差协方差阵更新，Pk+1=(I-LkCk)Pk.
按上述6个步骤进行反复迭代，便可实现对锂电池系统状态的强跟踪最优估计.
3 仿真实验设计
首先给出算法的参数和初值，ρ=0.95，β=1.2，x0=[40%，0，0]T，P0=I3×3，Q=diag(0.001，0.1，0.1).
为了验证算法对系统模型不准确和状态突变的强跟踪能力，本文在开路电压中加入均值为0.01，方差为0.1的随机噪声，并设计了带有电流突变的脉冲充放电实验.实验的数据采集频率为1 Hz，共采集了8 320个数据点，采集结果如图3所示.
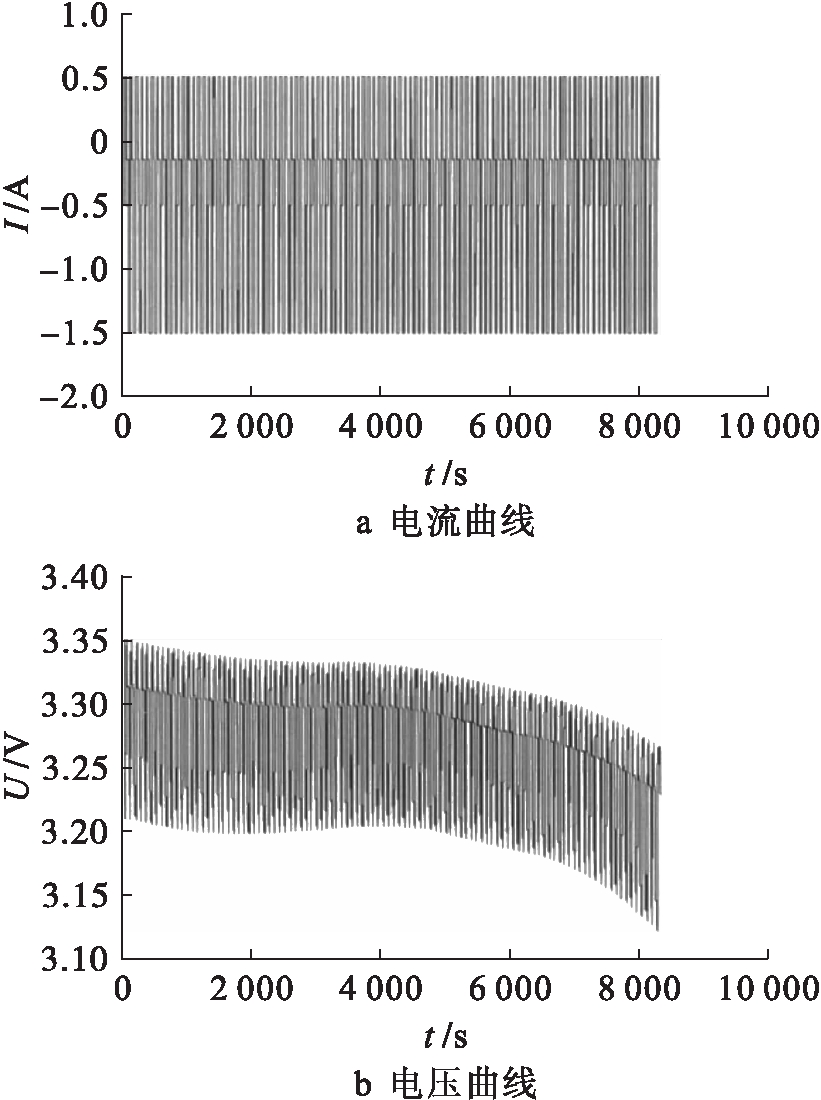
图3 数据采集结果
Fig.3 Data acquisition results
根据Uoc-qSOC关系式可知，电池qSOC初值为80.5%，但为了验证算法对初始误差的反应速度，将qSOC初值设置为80%，分别使用扩展卡尔曼滤波和强跟踪卡尔曼滤波对电池qSOC进行估计，其结果如图4所示.
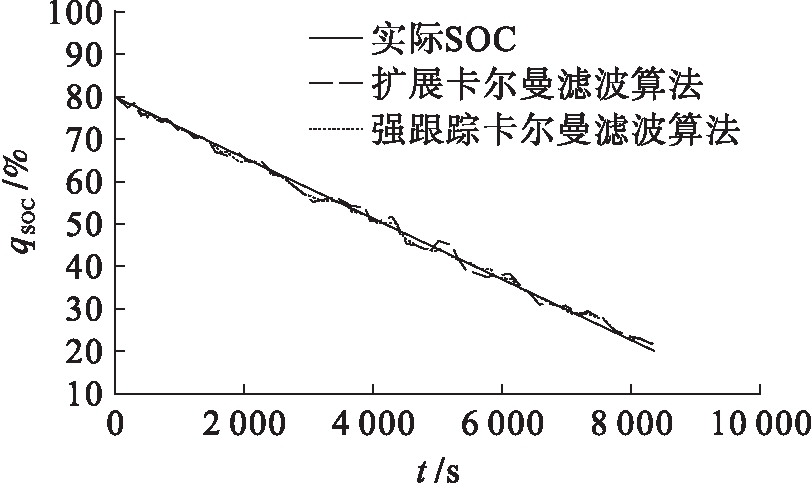
图4 两种算法的电池SOC估计结果
Fig.4 Battery SOC estimation results of two algorithms
为了观察两算法对初始误差的修正能力，对前50个数据进行局部放大，结果如图5所示.
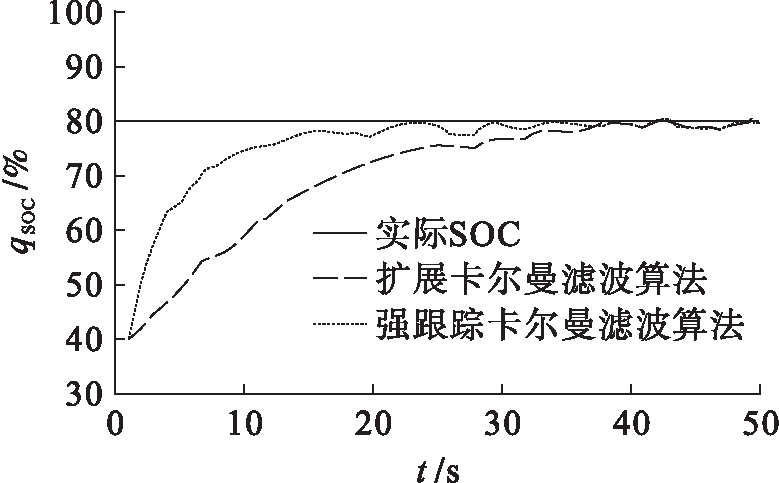
图5 前50个数据放大图
Fig.5 Enlarged diagram for ahead 50 data
从图5中可以看出，两种算法最终均可收敛到真值，但强跟踪卡尔曼滤波算法在20 s时就实现了真值跟踪，而扩展卡尔曼滤波在40 s时才收敛到真值，这充分说明了强跟踪卡尔曼滤波比扩展卡尔曼滤波具有更快的收敛速度与强跟踪特性.两种算法的估计误差曲线如图6所示.
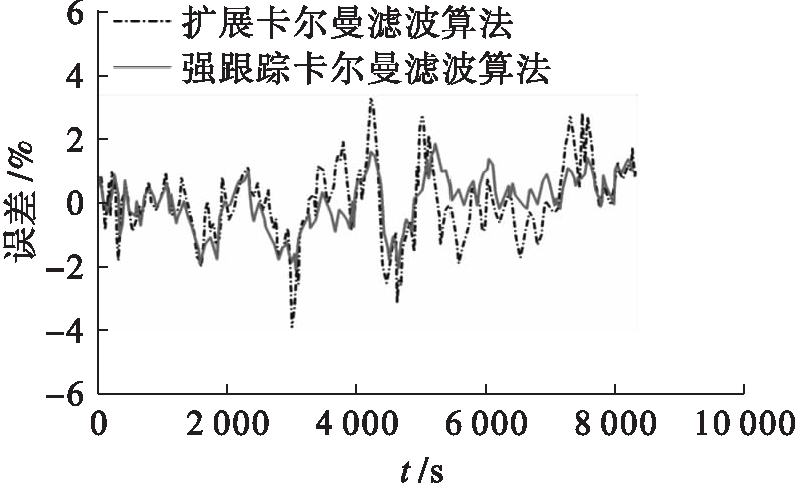
图6 估计误差曲线对比
Fig.6 Comparison in estimation error curves
由图6可以看出，在系统模型不准确和带有电流突变的情况下，强跟踪卡尔曼滤波的估计误差维持在2.5%之内；而扩展卡尔曼滤波的最大估计误差达到了4%.这是因为强跟踪卡尔曼滤波通过调整增益矩阵，使残差强行满足正交特性，残差变为高斯白噪声.这样既提高了算法的估计精度，又使算法快速向真值靠近，提升了算法收敛速度和突变跟踪能力.通过对比可以看出，在系统模型不准确和状态突变的情况下，本文提出的强跟踪卡尔曼滤波具有较高的估计精度.
4 结 论
经过以上分析，本文得出以下结论：
1) 双阶RC模型可更好模拟锂电池内部充放电过程，具有较高的建模精度；
2) 通过调节卡尔曼滤波增益，使残差具有高斯白噪声特性，提高了算法估计精度，减少了算法收敛时间；
3) 强跟踪卡尔曼滤波算法在应对状态突变和模型不准确等情况时，具有较高的估计精度.
参考文献(References)：
[1] 齐仁龙，朱小会，张庆辉.光伏发电系统暂态特性仿真 [J].沈阳工业大学学报，2017，39(2)：121-126.
(QI Ren-long，ZHU Xiao-hui，ZHANG Qing-hui.Simulation for transient characteristics of photovoltaic power generation system [J].Journal of Shenyang University of Technology，2017，39(2)：121-126.)
[2] 涂涛，钟其水，李波.锂电池荷电状态估算Matlab仿真研究 [J].电子设计工程，2016，24(20)： 129-132.
(TU Tao，ZHONG Qi-shui，LI Bo.The Matlab simulation research for the SOC estimation of lithium-ion battery [J].Electronic Design Engineering，2016，24(20)： 129-132.)
[3] 杨春生，牛红涛，隋良红，等.基于贝叶斯正则化算法BP神经网络钒电池SOC预测 [J].现代电子技术，2016，39(8)： 158-161.
(YANG Chun-sheng，NIU Hong-tao，SUI Liang-hong，et al.Application of BP neural network improved by Bayesian regularization algorithm in VRB SOC prediction [J].Modern Electronics Technique，2016，39(8)： 158-161.)
[4] 付浪，杜明星，刘斌，等.基于开路电压法与卡尔曼滤波法相结合的锂离子电池SOC估算 [J].天津理工大学学报，2015，31(6)：9-13.
(FU Lang，DU Ming-xing，LIU Bin，et al.Estimation of lithium-ion battery SOC based on combination of open-circuit voltage and Kalman filter [J].Journal of Tianjin University of Technology，2015，31(6)：9-13.)
[5] 鲍慧，于洋.基于安时积分法的电池SOC估算误差校正 [J].计算机仿真，2013，30(11)：148-151.
(BAO Hui，YU Yang.State of charge estimation calibration based on ampere-hour method [J].Computer Simulation，2013，30(11)：148-151.)
[6] 吴明泽.“开路电压法”电动汽车电池电量计算与行驶里程预测 [D].成都：电子科技大学，2013.
(WU Ming-ze.“The open circuit voltage method” electric vehicle battery mileage calculation and prediction [D].Chengdu：University of Electronic Science and Technology of China，2013.)
[7] 易明亮.基于内阻法的电池健康状态估计技术研究 [D].杭州：杭州电子科技大学，2012.
(YI Ming-liang.The technology research of battery health state estimation method based on the internal resistance [D].Hangzhou：Hangzhou Dianzi University，2012.)
[8] 黄耀波，唐海定，章欢，等.基于遗传神经网络的电动汽车锂电池SOC预测 [J].机电工程，2013，30(10)：1255-1258.
(HUANG Yao-bo，TANG Hai-ding，ZHANG Huan，et al.Prediction of lithium-ion battery SOC in EV based on genetic neural network [J].Journal of Mechanical & Electrical Engineering，2013，30(10)：1255-1258.)
[9] 韩忠华，刘珊珊，石刚，等.基于扩展卡尔曼神经网络算法估计电池SOC [J].电子技术应用，2016，42(7)：76-78.
(HAN Zhong-hua，LIU Shan-shan，SHI Gang，et al.Estimation of battery SOC based on extended Kalman filter with neural network algorithms [J].Application of Electronic Technique，2016，42(7)：76-78.)
[10]Zhang H，Chow M Y.Comprehensive dynamic battery modeling for PHEV applications[C]//Power and Energy Society General Meeting.California，USA，2010：1-6.
[11]周武生.电动汽车磷酸铁锂电池建模及荷电状态估计研究 [D].南昌：南昌航空大学，2015.
(ZHOU Wu-sheng.Research on modeling and SOC estimation for LIFEPO4 battery of electric vehicle [D].Nanchang：Nanchang Hangkong University，2015.)
[12]刘浩.基于EKF的电动汽车用锂离子电池SOC估算方法研究 [D].北京：北京交通大学，2010.
(LIU Hao.Study on SOC estimation method of lithium-ion battery based on EKF for electric vehicles [D].Beijing：Beijing Jiaotong University，2010.)
[13]王长清，朱敏.基于复合EKF算法的锂电池组的SOC估计 [J].电源技术，2015，39(2)：285-286.
(WANG Chang-qing，ZHU Min.A new estimation method of li-batteries SOC based on composite EKF [J].Chinese Journal of Power Sources，2015，39(2)：285-286.)
[14]张娟.基于远程监控系统的纯电动汽车锂离子电池SOC估算算法研究 [D].长春：吉林大学，2014.
(ZHANG Juan.Study on SOC estimation algorithm of lithium-ion battery based on remote monitoring system for pure electric vehicle [D].Changchun：Jilin University，2014.)
[15]冯光.基于EKF的锂离子电池SOC估算的建模与仿真 [D].武汉：武汉理工大学，2013.
(FENG Guang.Modeling and simulation based on EKF lithium-ion battery SOC estimation [D].Wuhan：Wuhan University of Technology，2013.)
[16]胡新宇，张锋，王博思，等.基于EKF的18650锂电池SOC在线估算 [J].激光杂志，2016，37(5)：72-75.
(HU Xin-yu，ZHANG Feng，WANG Bo-si，et al.On-line estimation of 18650 lithium battery SOC based on extended Kalman filtering [J].Laser Journal，2016，37(5)：72-75.)
[17]荣雅君，杨伟，牛欢，等.基于BP-EKF算法的电动汽车电池管理系统SOC精准估计 [J].电工电能新技术，2015，34(9)：22-28.
(RONG Ya-jun，YANG Wei，NIU Huan，et al.Accurate estimation of SOC value of electric vehicle battery based on EKF algorithm optimized by BP neural network [J].Advanced Technology of Electrical Engineering and Energy，2015，34(9)：22-28.)
[18]陈林，张持健，殷安龙，等.基于LabVIEW的锂电池监测系统及SOC预测研究 [J].电子设计工程，2016，24(15)： 73-75.
(CHEN Lin，ZHANG Chi-jian，YIN An-long，et al.Lithium battery monitoring system based on LabVIEW and research on the prediction of SOC [J].Electronic Design Engineering，2016，24(15)： 73-75.)