由于具备恒定包络，连续相位调制(CPM)经常被用于无线通信领域.目前，由于人们认为接收器的解调制和同步过于复杂，CPM仅用于现代无线电领域，其应用范围受到限制.最初，文献[1]将最大似然(ML)解调制技术用于CPM，但是该方案需要相当大的计算成本.文献[2]提出以Laurent分解为基础，利用脉冲幅度调制(pulse amplitude modulation，PAM)有效地使CPM信号线性化，该技术显著降低了检测器的复杂度，同时并未对其性能产生影响.对于接收器的同步而言，也有许多方法对载波频率、相位以及符号定时参数进行估计[3].通常，同步方法可分为数据辅助(data aided，DA)方案和非数据辅助(non data aided，NDA)方案，前者使用相干检测，后者使用非相干检测.对于CPM同步而言，其中一个最大的难题就是如何获得可靠的符号定时信息.采用相干DA方法能够增强可靠性，但用于符号定时估计的ML方案同时包含了定时转移的非线性函数以及复杂的导数运算，这会导致采用相干DA方法的计算成本显著增加.
多位研究人员提出通过CPM信号的基函数展开法解决了上述问题.文献[4]使用了指数函数，而文献[5-6]分别使用了PAM和沃尔什函数.虽然上述方法均能将定时误差表示为信号的线性函数，但是依然存在复杂的导数运算.
本文提出利用基函数的替代集合(以勒让德多项式的形式)来更好地逼近CPM信号.该方法能够使ML方案中的定时转移线性化，并且使导数运算变为简单求和.对于多个常用CPM信号而言，得出的定时估计接近于修正的克拉美罗限(modified Cramer-Rao bound，MCRB)[7].
1 系统模型
传输基带CPM信号的复包络可表示为
(1)
式中：E为每个符号的能量；T为符号持续时间；φ(t，α)为N个符号的信息承载相函数，其表达式为
(2)
其中，αn为从集合{±1，±3，…，±(Mc-1)}取得的符号序列
t-∞g(t)dt为由持续时间为LT的频率脉冲g(t)确定的相位响应，L为一个整数，表示频率脉冲的长度.
在接收器内，带有符号定时偏差τ的基带信号可被建模，其表达式为
r(t)=s(t-τ，α)+w(t)
(3)
式中，w(t)为零均值高斯噪声，功率谱密度为N0.
假设突发的接收信号包含一个随机生成的已知前导序列α，并且定时不确定性只限于τ=±T/2，在观察期间T0=NT内未知符号定时参数的对数似然函数可表示为
(4)
式中：*为复共轭
为符号定时的假设值；Re{·}表示实数部分.
1.1 数据辅助检测
由式(4)可知，相位调制方案中使用了最大化该公式的符号定时估计.为了解决此问题，本文用一组K正交基函数
来表示信号，因此，信号可表示为
(5)
式中，
sn，k构成了nth符号以及kth基函数的投影系数.将式(5)代入式(4)，并将积分分成N个部分的总和，可得
(6)
式中，
(7)
通过取得对数似然函数的导数并将结果设置为零，就能够获得使定时误差估计变为最大似然估计的必要条件.在去除常数并进行重新排列之后，DA对数似然函数可表示为
(8)
对式(7)中的参数进行
替换，可以得出
可被视为通过导数滤波器接收信号的采样输出值.
1.2 勒让德多项式设计
在文献[8]中，当K=2时，勒让德多项式提供了足够的精确度，能够逼近常见的CPM信号.实际上，为了不失一般性，设置时间转移时的勒让德多项式的范围为[0，T].因此，当k=0、1时，获得了正交时间转移基函数φ0(t)=1以及φ1(t)=2t/T-1，相应的导数计算滤波器的正交时间转移基函数可表示为
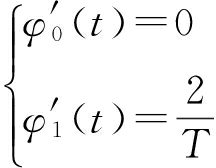
(9)
将式(9)代入式(8)，以便减少公式计算项，可得
(10)
式中，
(11)
在这种情况下，可发现采用本文提出的方法之后首次降低了复杂度.当K=2时，每组导数计算滤波器就会进行简单求和，并且对接收信号进行缩放，如式(11)所示.
目前，
值是最大似然估计的近似值，会使式(10)左边消失.为了生成该数值，本文使用了特定CPM方案中的S形曲线特性.
1.3 S形曲线
S形曲线S(τ)为关于定时误差τ的对数似然函数导数的平均值.本文利用式(10)中已知的前导序列近似S形曲线，对N个符号的近似可表示为
(12)
ML定时估计与S形曲线正斜率上的零交叉点相对应.获得估计的方法是生成整个S形曲线，并确定零交叉点.但如果只是希望对单点进行估计，计算过程会相当繁琐.文献[8]提出了一种更加有效的方法，即通过假设最坏情况下的定时误差τ=±T/2，并且评估稍微宽的范围±3T/4内的S形曲线进行估计.基于此，在时间实例中对式(12)进行了评估，即
(13)
式中，m为S形曲线进行均匀采样的数值(整数)，在序列中P=1.5m+1.为了对S形曲线的离散样本进行评估，两个样本应满足S(τi)<0且S(τi)S(τi+1)<0，通过线性插值发现最终近似定时误差相当于ML估计，则有
(14)
因此，定时估计器的工作过程为：以样本τi，i=0，1，…，P-1为例，根据式(12)对近似S形曲线进行计算；根据式(13)识别零交叉点；根据式(14)实现近似符号定时估计.
2 接收器结构设计
本文提出的方法能够用于开环结构中，因此，通过N个前导符号实现的符号定时估计，能够用于校正数据符号的定时误差.但是，对于闭环恢复电路而言，通常依赖的是根据前导符号进行的初始定时估计，然后是判决引导(decision directed，DD)模式下的定时估计，这是利用接收器的数据判决实现的.文献[5]从CPM解调器获得了数据判决，实现了维特比算法，根据回溯深度延迟判决，用D表示.根据此方法，绘制出了带有数据检测的闭环定时恢复接收器的方框图，如图1所示.图1中，在Ts=T/U的时间条件下对接收信号进行取样，其中，U表示抽样次数的整数.通过输入值为r(kTs)=r((uk+μk)Ts)的内插器对信号进行馈电，其中，uk和μk分别表示基点指数和小数偏差，根据当前定时估计
对输入样本进行调整[9].利用K=2的实值滤波器以及一个实值导数滤波器对内插信号进行处理，因数U致使滤波器的输出值大幅下降.通过检测器利用抽取的信号生成数据判决
并生成定时误差检测器(timing error detector，TED)的输入值.对于TED而言，在逐符号的基础上，输出端的误差信号等同于式(12)，可表示为
(15)
一旦对误差信号进行了计算，环路滤波器就会提供一种带有更新值的新型定时估计，即
(16)
式中，λ表示与归一化等效噪声带宽相关的步长.最后由定时控制确定uk=⎣
其中，⎣z」表示内插算法中不超过z的最大整数.
3 仿真结果
3.1 开环系统实验结果
为了验证符号定时估计器的性能，本文将提出算法的定时误差方差与MCRB进行了比较.假设定时误差独立并且均匀地分布在τ=±T/2范围内，首先利用式(12)～(14)在200个符号内随机生成前导信号.需注意的是，选取随机前导以确保本文提出的方法能够适用于任意一种指定的前导结构.
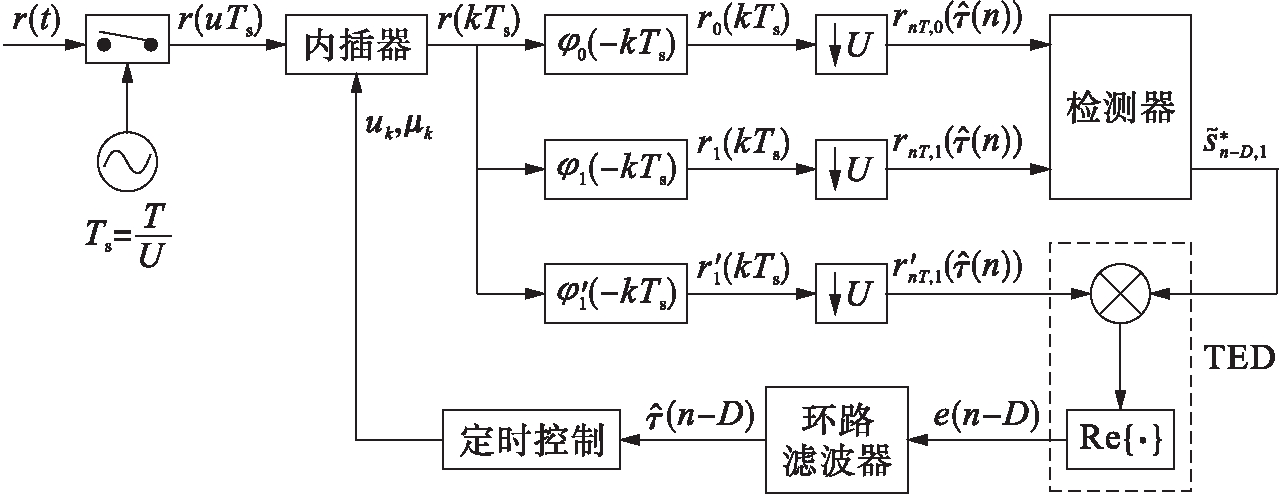
图1 闭环定时恢复电路框图
Fig.1 Block diagram of closed loop timing recovery circuit
图2是两种常用CPM方案，即最小频移键控(minimum shift keying，MSK)和高斯MSK(GMSK)的归一化定时误差方差.在上述两种方案内，在速率T/m的条件下对S形曲线进行了取样，其中，在两种方案内分别为m=2和4.从图2中可看出，相较于m=2，在m=4时采取的样本与较大噪声范围内对应的MCRB十分接近.由于内插算法的精确度是随着m值的增加而提升，该结果符合预期.经过观察可以看出，在噪声较大的情况下，提出的算法十分接近MSK和GMSK中Es/N0≤0 dB和Es/N0≤10 dB的界限，其中，Es/N0表示符号能量与噪声功率谱密度之间的比率.
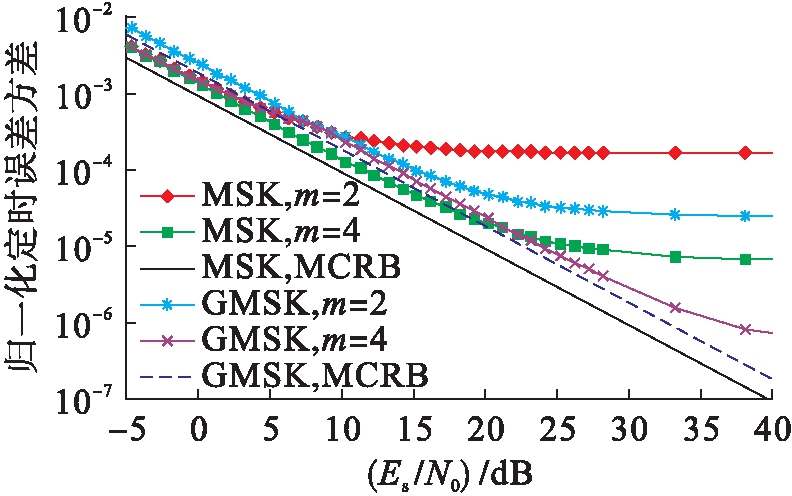
图2 MSK和GMSK归一化定时误差方差
Fig.2 Normalized timing error variancein MSK and GMSK
随着m值的增加，本文希望MSK的性能优于GMSK，但是图2显示的结果却违反了这个预期.在L=1的MSK方案中，线性函数在符号周期内并不具有信号相变的特点.因此，在构成S形曲线并且定时估计不精确的时候出现了近似误差.但是在L≈3的GMSK方案中，线性函数较好地逼近了相位，这一点与S形曲线近似以及定时估计的精确度提升一致.通常，L≥2并且h≤0.5的CPM信号在符号间隔内具有线性相变的特点，并且基函数对其进行了较好地逼近.由于L降低或者h增加，相位变化不再与线性函数类似，同时近似精确度也会降低.为了进一步说明，本文考虑使用两个候选的逼近容量CPM方法[10-11]，其中，参数为Mc=4、2RC(RC表示g(t)由升余弦函数调制产生)，进制位h=1/8以及Mc=2、4REC(REC表示g(t)由矩形脉冲函数调制产生)，h=1/4.在这种情况下，在较大的Es/N0范围内与MCRB十分接近，在Es/N0≤15 dB的条件下，m=2与m=4之间的差异较小，如图3所示.
3.2 闭环系统实验结果
对于闭环系统而言，假设定时残留误差为τ=0，可以在DD模式下对其性能进行检测.这种情况是人为设计的，但是能够观察到错误的数据判决对定时误差方差的影响.在DD模式下，数据部分包含大约550个符号，并且确定回溯值D=1.图4、5为环路带宽为2.5e-3时DD定时的性能.显然，在MSK和GMSK两种方案中，符号定时估计器表现出了鲁棒性能，十分接近较大噪声值的界限，但是偏离了MCRB，即出现了近似误差.从图5(参数为Mc=4、2RC，h=1/8以及Mc=2、4REC，h=1/4)中可看出相似的趋势，高阶参数方案对近似误差更加敏感，原因在于在符号间隔内的相位变化不再逼近线性函数.但在所有情况下，闭环系统均能够在一定信噪比范围内实现可信的定时估计，该范围是在调制方案的工作范围内.
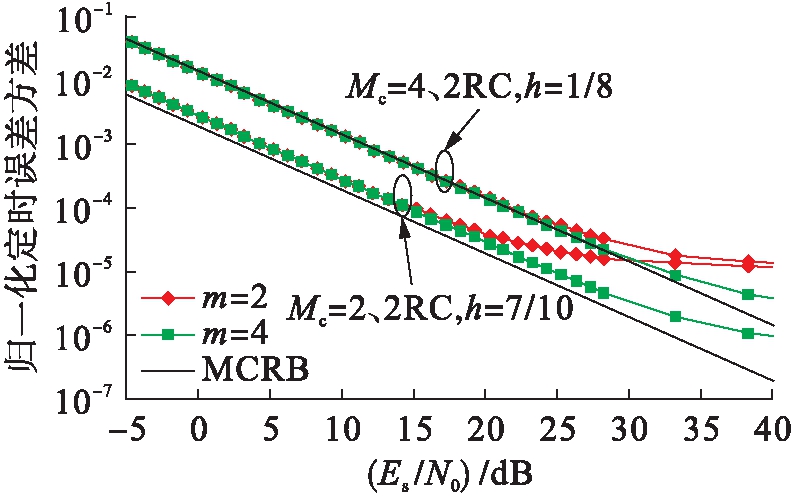
图3 在两个逼近容量CPM方案中的归一化定时误差方差
Fig.3 Normalized timing error variance in twoapproximation capacity CPM schemes
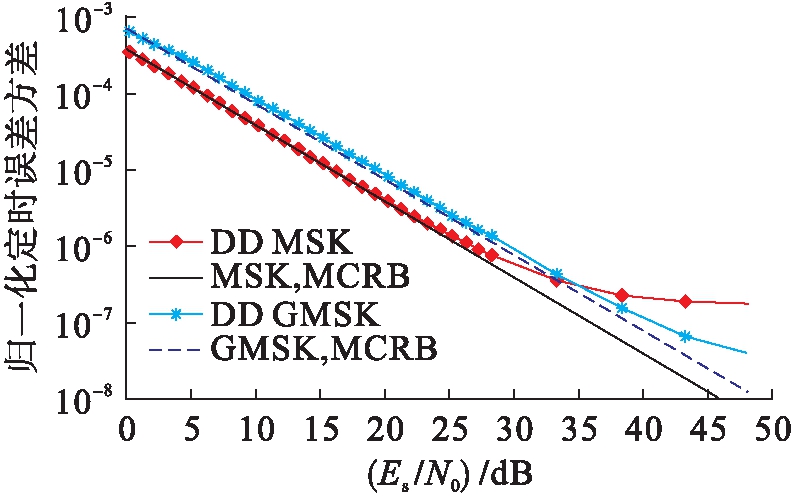
图4 DD模式下MSK和GMSK方案内的归一化定时误差方差
Fig.4 Normalized timing error variance in MSK and GMSK schemes under DD mode
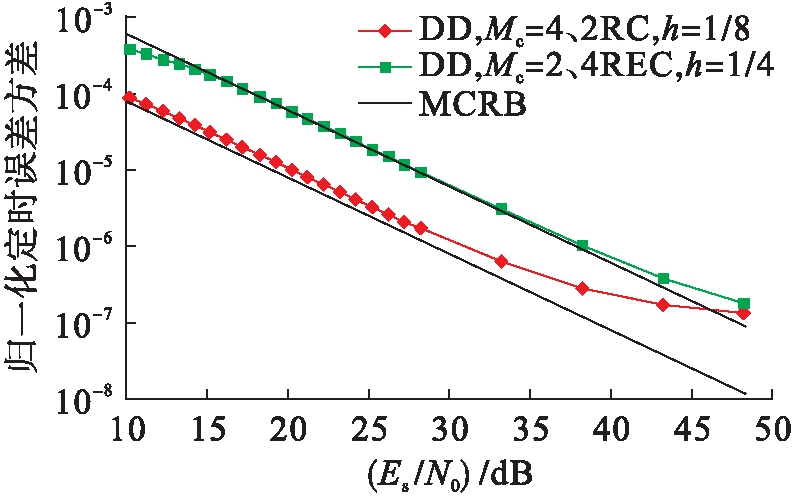
图5 DD模式下两个逼近容量CPM方案中的归一化定时误差方差
Fig.5 Normalized timing error variance in two approximationcapacity CPM schemes under DD mode
3.3 算法复杂度分析
为了分析算法实现成本，对本文提出方案的复杂度进行了比较.在文献[4]中，为了进行求导，每个符号需要12(LoM+(L-1)A)次运算，其中，乘法次数为M，加法次数为A，Lo表示匹配滤波器的样本长度，需要3M+A次运算来实现定时估计.在文献[5]中，为了进行求导，需要4(LoM+(L-1)A)次运算，以及3M+A次运算来实现定时估计.在本文中，只需通过mLo次加法运算就能够实现导数运算，并且通过12M+11A次运算实现了定时估计，比较结果如表1所示.由表1可知，本文提出方法的整体计算成本更低.
表1 不同算法的运算复杂度比较
Tab.1 Comparison in computational complexityof different algorithms
4 结 论
本文提出了一种新型低复杂度的CPMML定时估计方案.利用基函数的替代集合(以勒让德多项式的形式)来更好地逼近CPM信号.该方法能够使ML方案中的定时转移线性化，并且使导数运算变为简单求和.结果表明，对于各种CPM参数而言，在开环以及闭环两个系统中，本文提出算法的估计性能与MCRB相近.
参考文献(References)：
[1] Bellili F，Meftehi R，Affes S，et al.Maximum likelihood SNR estimation of linearly-modulated signals over time-varying flat-fading SIMO channels [J].IEEE Transactions on Signal Processing，2014，63(2)：441-456.
[2] Peral-Rosado J A D，López-Salcedo J A，Seco-Granados G，et al.Joint maximum likelihood time-delay es-timation for LTE positioning in multipath channels [J].EURASIP Journal on Advances in Signal Processing，2014(1)：1-13.
[3] 周相超，薛睿，赵旦峰，等.连续相位调制信号的载波相位软同步算法 [J].吉林大学学报(工学版)，2015，45(1)：291-296.
(ZHOU Xiang-chao，XUE Rui，ZHAO Dan-feng，et al.Carrier phase soft synchronization algorithm for continuous phase modulated signals [J].Journal of Jilin University (Engineering Science Edition)，2015，45(1)：291-296.)
[4] Cariolaro G，Cipriano A M.Minimal PAM decompositions of CPM signals with separable phase [J].IEEE Transactions on Communications，2014，53(12)：2011-2014.
[5] Chen Y.Semiparametric time series models with log-concave innovations：maximum likelihood estimation and its consistency [J].Scandinavian Journal of Statistics，2015，42(1)：1-31.
[6] Dehay D.Parameter maximum likelihood estimation problem for time periodic modulated drift Ornstein Uhlenbeck processes [J].Statistical Inference for Stochastic Processes，2015，18(1)：1-30.
[7] Bialer O，Raphaeli D，Weiss A J.Efficient time of arrival estimation algorithm achieving maximum likelihood performance in dense multipath [J].IEEE Transactions on Signal Processing，2012，60(3)：1241-1252.
[8] O’Shea D，Mcgrath S.A novel interpolation method for maximum likelihood timing recovery [J].Wireless Personal Communications，1997，4(3)：315-324.
[9] 周荣，刘爱军，潘克刚，等.基于判决反馈的CPM信号定时相位联合估计算法 [J].通信技术，2015，48(2)：146-150.
(ZHOU Rong，LIU Ai-jun，PAN Ke-gang，et al.A joint estimation algorithm for CPM signal timing phase based on decision feedback [J].Communication Technology，2015，48(2)：146-150.)
[10]Perotti A，Tarable A，Benedetto S，et al.Capacity-achieving CPM schemes [J].IEEE Transactions on Information Theory，2010，56(4)：1521-1541.
[11]郭黎利，周彬，孙志国，等.基于FRFT滤波的SNCK通信系统接收方法 [J].沈阳工业大学学报，2013，35(6)：672-679.
(GUO Li-li，ZHOU Bin，SUN Zhi-guo，et al.Recei-ving method of SNCK communication system based on FRFT filter [J].Journal of Shenyang University of Technology，2013，35(6)：672-679.)