边坡是一种复杂的地质体，具有未知性、随机性、模糊性和可变性等特点，据统计，每年所造成的直接经济损失多达50～60亿元[1].风险分析通过查明系统中的各种不确定性因素，对其存在的危险性做出分析与评价，对于确保边坡工程的长期稳定和安全性具有重要的意义[2-3].目前，用于边坡风险评价的方法主要有定性分析法、定量分析法和综合分析法，例如德尔菲法、智爆法、蒙特卡罗法、概率统计法和敏感性分析法等[4-5].但是这些方法或多或少都存在缺陷，具有多属性、不相容、定性与定量综合评价的问题，如德尔菲法难以准确量化，概率统计法中数据收集往往比较困难，且计算过程复杂[6].
因此，本文提出了基于马尔科夫链法和物元可拓法来建立动态的边坡风险评价模型(MC-EE)，该综合评价模型对多维数据进行动态分析，以寻求新的方法和途径来认识风险本质和风险因子的性质和相互联系，追踪和预测边坡风险的变化规律.该模型的优点是简单、容易掌握，对于多层次、多因素的复杂问题评判效果较好，很好地弥补了前述方法缺乏预测性和时效性差的缺陷，在减少人为主观因素影响、提高评价结果的可靠性和时效性等方面，均起到了很好的作用.本文在详细介绍该模型的原理、特点和算法后，将其应用于实际边坡工程的风险评价中，实例检验其可行性及效果.
1 风险评价模型
1.1 物元可拓法
物元可拓理论(element extension theory，EE)[7-10]的基本思想是引入物元把处理研究对象间的矛盾问题变成处理物元之间的矛盾问题，将边坡工程风险评价中的矛盾问题转化为相容问题，从边坡系统的组成部分和内外关系去研究其安全性能，目前已广泛应用于各个领域，其具体步骤如下.
1) 确定边坡风险状态评价的物元.假定边坡的名称为N，对应边坡风险特征C的量值为V，有序三元组R=(N，C，V)称为物元，其表达式为
R= (N，C，V)=
[对象特征c1特征值v1
特征c2特征值v2⋮⋮
特征cn特征值vn]=[R1R2⋮Rn]
(1)
2) 建立评价模型，过程如下：
① 计算边坡风险评价的单指标关联函数.依次选择某一待评物元，计算其关于各等级的关联度，判定所属等级.把该待评对象N的第i个特征关于第j级别的关联函数记为rj(vi(t))，i=1，2，…，n；j=1，2，…，m，具体的计算过程为
{rj(vi(t))=ρ(vi(t)，〈a0ij，b0ij〉)b0ij-a0ij(vi(t)∈〈a0ij，b0ij〉)
rj(vi(t))=ρ(vi(t)，〈a0ij，b0ij〉)ρ(vi(t)，〈api，bpi〉)-ρ(vi(t)，〈a0ij，b0ij〉) (vi(t)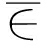
〈a0ij，b0ij〉)
(2)
式中，
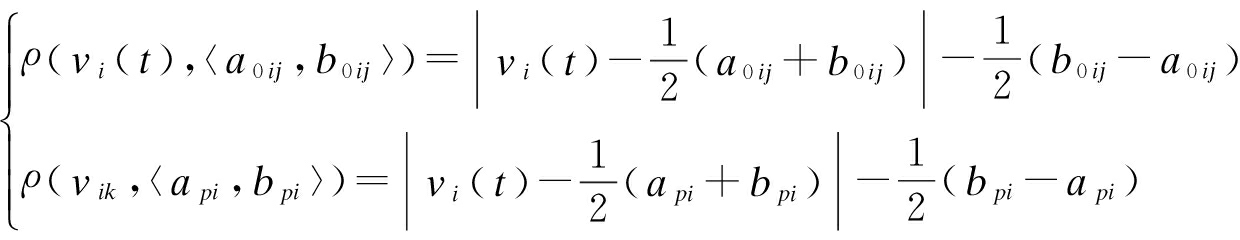
(3)
其中，各变量的含义见文献[7].
② 计算多指标综合关联度.待评对象N关于级别j的关联度计算公式为
(4)
式中，wi为第i个评价指标的权重分配系数，
③ 确定边坡风险级别的关联度.采用熵权法[11-12]来确定各指标的权系数，求得边坡风险状态针对各级别的关联度Kjt，之后根据公式Kt(N)=max{Kjt(N)}即可判定待评边坡N的安全级别属于等级t，t为待评价边坡所属风险级别的特征值，其表达式为
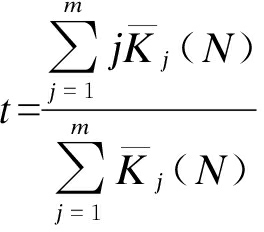
(5)
式中，
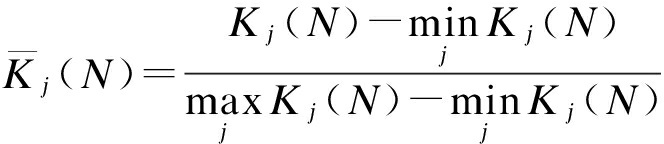
(6)
详细的物元可拓评价模型的计算流程如图1所示.
1.2 马尔科夫链法
马尔科夫链法(Markov chain，MC)[13]的基本思路是对满足马尔科夫性的某事物，利用其状态转移概率来研究其动态变化和未来发展趋势.该方法具有较高的准确性和科学性，适用于随机波动性较大的时序，在现代预测方法中占有重要的地位，并逐步应用于资源科学、地质学、经济领域和自然灾害学等各个领域.
设{Xk，k≥0}为马尔科夫链，样本数据X1，X2，…，Xk为马尔科夫链的指标值序列，选取距离预测时间最近的P个时步，依据距离的远近将转移步数依次定为1，2，…，P.求出各转移步数对应的状态转移矩阵，从中选取起始状态所对应的行向量，将其组成新的概率矩阵G，对G的列向量求和，其和最大的转移步数所对应的状态即为该时间序列的发展趋势.
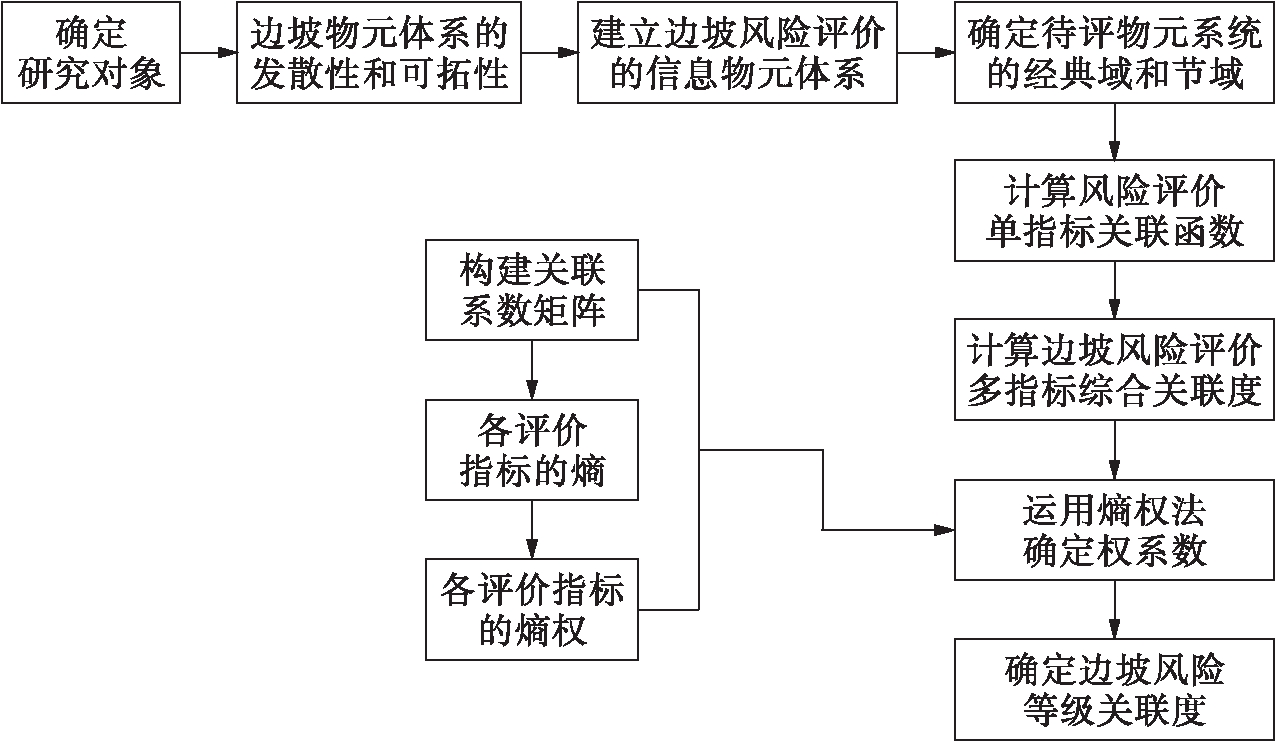
图1 边坡风险状态的可拓评价流程图
Fig.1 Flow chart of extension evaluation for state of slope risk
需要注意的是，在应用马尔科夫模型时需先检验是否符合马尔科夫性质.对离散序列的马尔科夫链通常采用χ2统计量来检验.对于边际概率
当m充分大时，统计量χ2=
服从自由度为(m-1)2的χ2分布.当
时，该序列符合马尔科夫性质，否则不能当作马尔科夫链来计算.
1.3 风险评价计算模型
由边坡风险定义可知，对其评价是由危险性评价和损失评价共同构成，描述不确定因素与风险事件发生概率的关系，以及不确定因素与可能损失之间的关系.因此，本文提出了基于马尔科夫链法和物元可拓法来建立边坡的风险评价数学模型，融合危险性评价和易损性评价二者所得到的失事概率和损失后果的计算结果用风险矩阵来分区表示，其优点是模型简单、容易掌握，对于多层次、多因素的复杂问题评判效果较好.
依据最低合理可行原则(ALARP)，表1为风险的级别及基本对策.
表1 风险的分级及相应对策
Tab.1 Risk grades and corresponding countermeasures
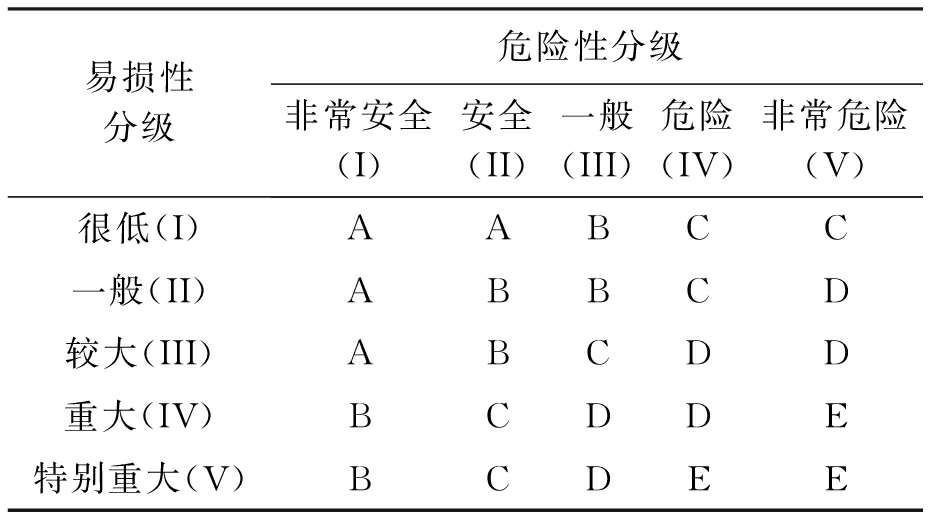
表2为按照上述可拓评价步骤计算得到的风险矩阵列表，由失效可能性和造成损失后果的五个级别两两排列组合，形成了一个5×5的矩阵.
该方法将边坡灾害、灾害特征和灾害特征值结合为一个整体，借助关联函数计算来实现边坡灾害的级别归属和安全性态的综合描述判断，实现了定性与定量综合集成评价，利于揭示各因素之间的相互依赖关系和影响结果，从而更完整、深刻地反映了灾害的本质，为边坡风险分析提供直观的查询和参考依据.
表2 风险评价矩阵列表
Tab.2 Matrix of risk assessment
2 工程应用
采用本文模型对某边坡工程进行动态风险评价研究.该边坡地处青藏高原向四川盆地过渡的斜坡地带，地质条件复杂，具有断层、层间挤压带等不良地质构造，工程边坡的安全稳定性问题非常突出.因此，对其开展风险研究和分析工作并进行合理地预测具有十分重要的意义.
2.1 确定风险等级
待评价边坡的风险评价物元表达式为R= (N，C，V)=
计算待评边坡N的第i个特征关于风险各等级的关联度，其表达式为
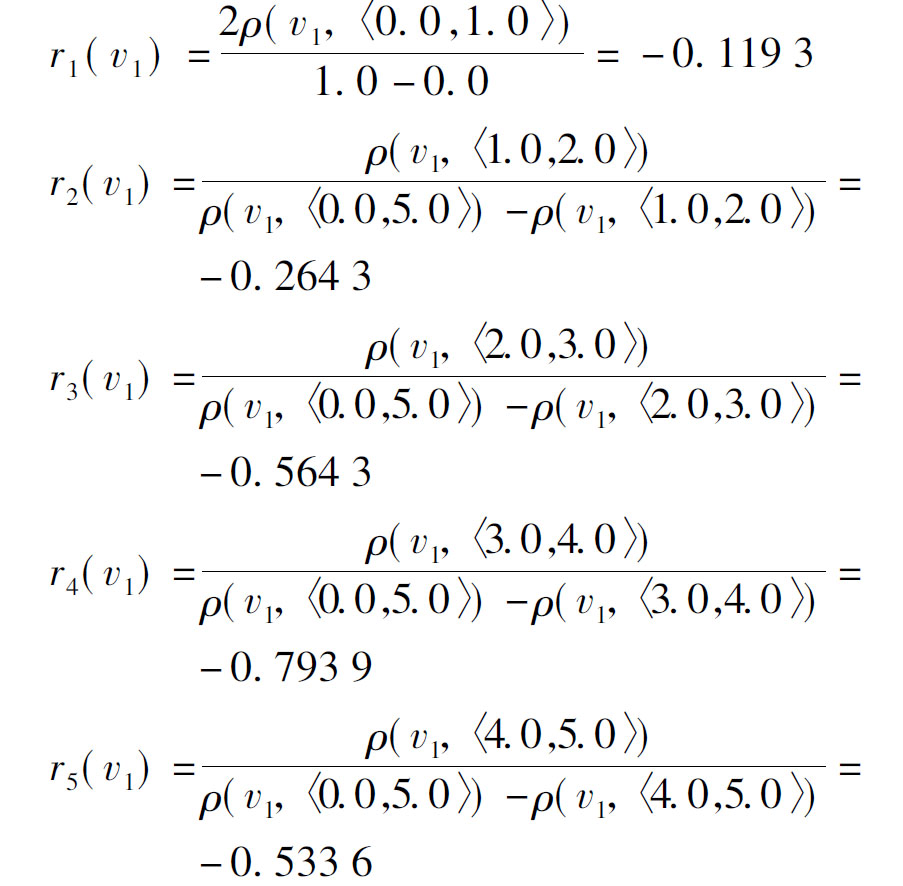
同理可以求得其他关联度，即
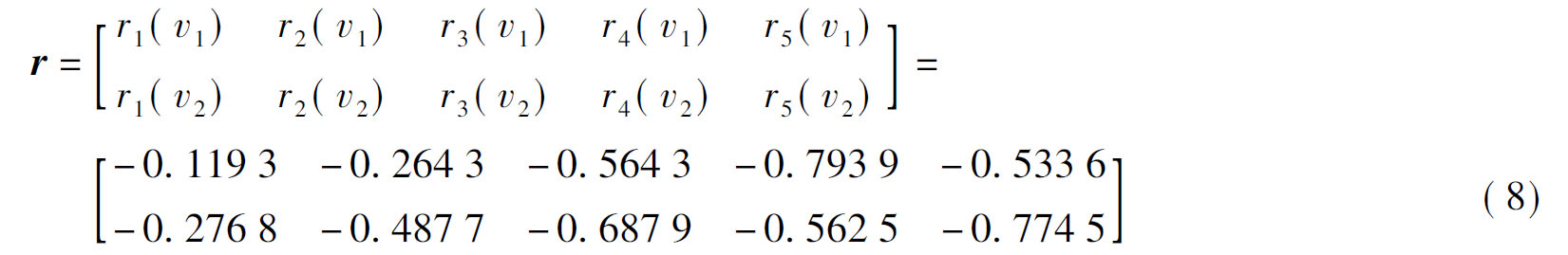
求出单指标关联度后，依据熵权法求得相应权系数值，并计算多指标关联度.该边坡关于各风险等级的关联度计算结果如表3所示.
表3 边坡物元可拓风险评价计算结果
Tab.3 Calculated results of matter-element
extension evaluation of slope risk
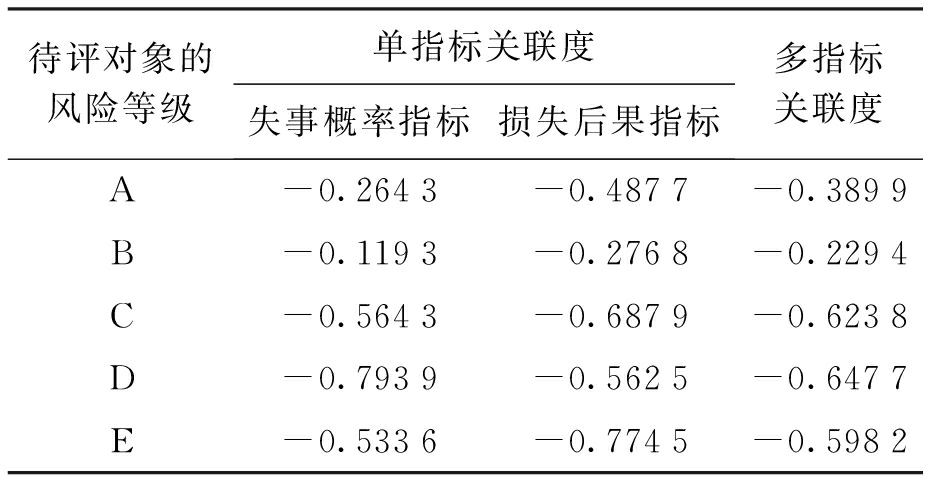
最后综合得出该边坡的安全情况属于B级，处于较低风险状态，即使发生事故，所造成的后果相对轻微，无需专门考虑和关注.该边坡工程的风险值处于可以接受的风险区域.
2.2 风险趋势分析
对于边坡工程来说，趋势性分析是风险评价的重要环节.由于监测数据中蕴含了大量丰富的变形信息，因此，本文根据已有的历史监测资料分析，采用马尔科夫链法智能挖掘和统计其安全演化规律并预测风险发展趋势.将边坡的监测位移时序划分为五个状态S1、S2、S3、S4、S5，界限划分结果如表4所示.
表4 状态类型的划分
Tab.4 Division of state typesmm
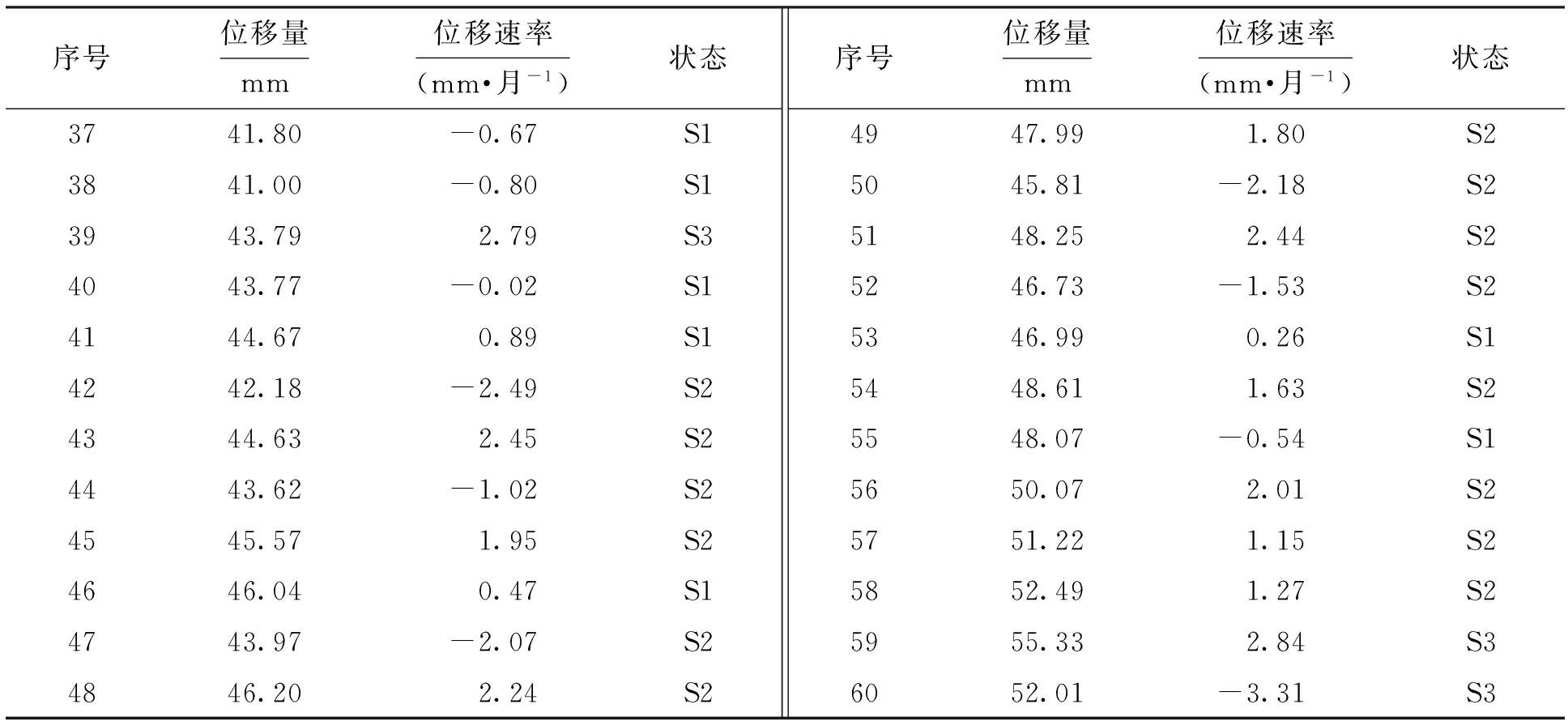
选取典型外观测点TPL7进行研究分析，该测点完整监控了边坡从开挖到现在的所有情况，包含安全等级的所有状态，利用其完整信息来研究演化的规律和发展趋势.表5列出了该观测点历年的部分实测数据.
根据公式
可以得到χ2的值为33.276 5，显著性水平α为0.05(即在原假设事实上正确的情况下，研究人员接受这一假设的可能性为95%)时，分位点
由于
所以监测值序列满足马尔科夫性质，故可采用马尔科夫链法来计算.各步长状态转移的概率矩阵为
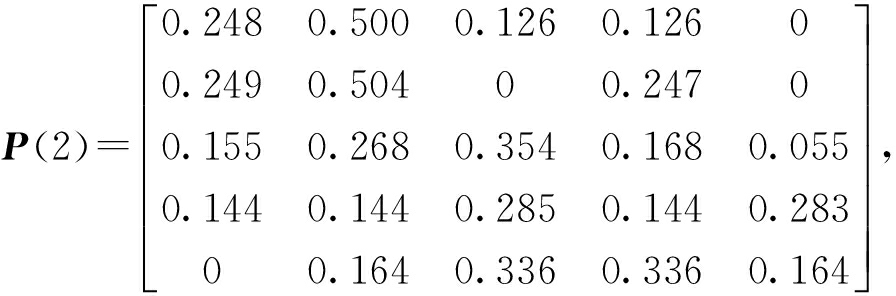
表5 部分年份的监测位移量及其等级
Tab.5 Monitoring displacement and grade in partial years
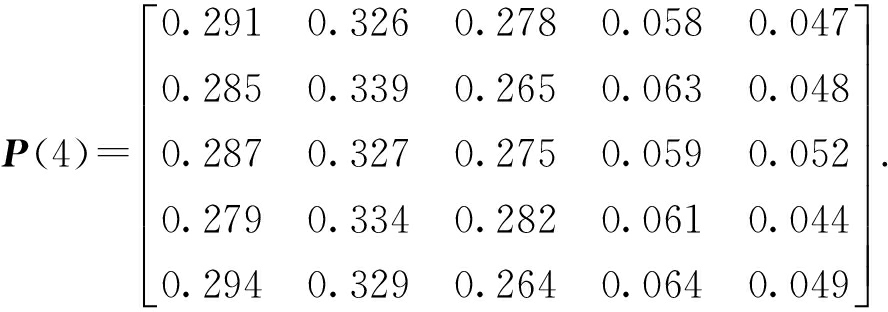
对该边坡从1～6月份的安全性进行预测，由于将时序划分为5个状态，所以选取离预测时间最近的时步编制预测表，转移步数按时步的远近分别定为1、2、3、4.在转移步数所对应的转移矩阵中，选取初始状态的行向量组成新的转移概率矩阵.对新的矩阵进行列向量求和，其和最大的转移步数所对应的状态即为系统的未来转向状态，相应的结果如表6所示.
由表6可知，各时序状态的预测概率叠加值分别为1.044、1.288、1.097、0.388、0.183，其中最大值为1.288，其预测所处的状态为S2，即该月的位移量约在53.01～54.51 mm之间，而实测位移是53.83 mm，处于该范围内，说明预测结果与实际情况相吻合.
表6 1月份边坡部位的风险状态预测
Tab.6 Risk state prediction of slope part in January
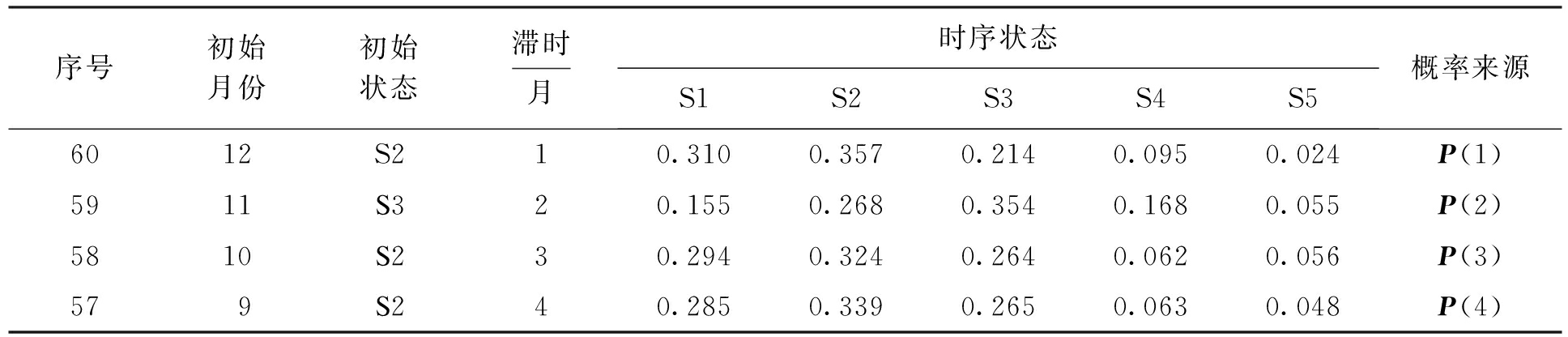
表7为2月份边坡部位的风险状态预测.由时序58～61号的实测值预测第62个时序的位移值，即2月份的监测值为53.46 mm，计算结果表明与实际相符合，进一步论证了该方法的合理性和科学性.对3～8月份的风险状态进行动态滚动预测，结果如表8所示.
表7 2月份边坡部位的风险状态预测
Tab.7 Risk state prediction of slope part in February
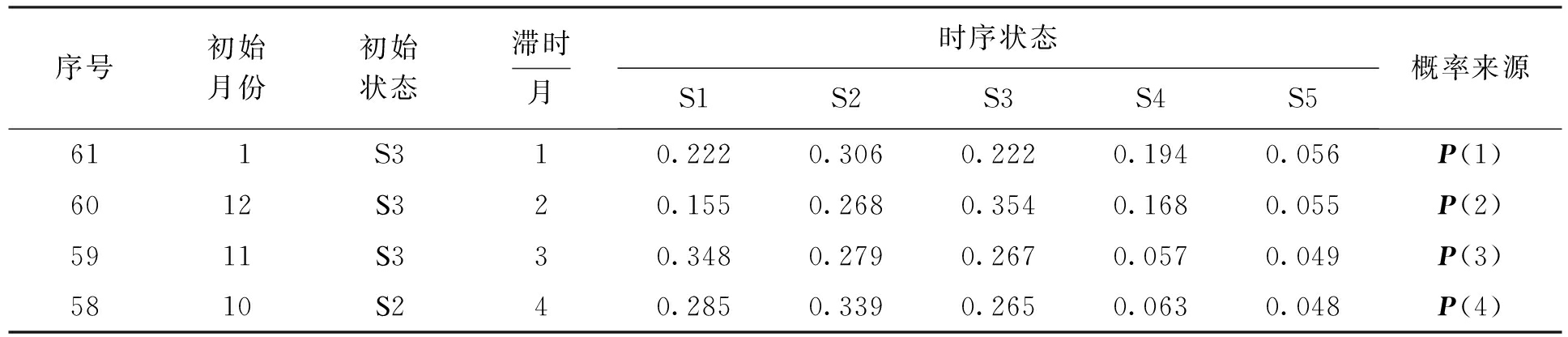
表8 位移时序的监测值与预测值
Tab.8 Monitored and predicted values ofdisplacement time sequence
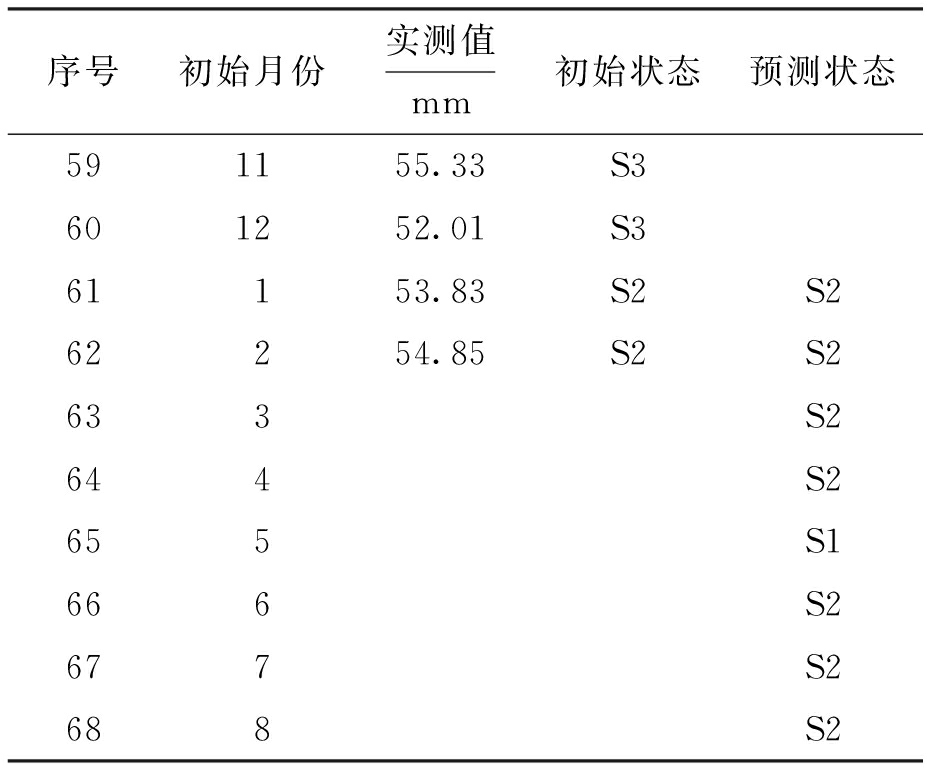
从预测结果可以看出，目前边坡的安全状态为较低风险，未来的半年时间内在“较低风险”和“低风险”之间波动，没有大的变化趋势，比较稳定，处于可以接受的风险状态，能够保证工程的正常运行.
3 结 论
本文通过分析得出以下结论：
1) 将物元可拓法和马尔科夫链法相结合，提出了一种动态追踪和预测边坡风险变化规律的评价模型(MC-EE).将该模型应用到边坡工程的风险研究中，显示了良好的预测效果，表明本文提出的MC-EE动态风险评价模型具有较好的实际应用价值.
2) 该模型从风险的概念出发，对数据动态递推分析，构建的风险矩阵完成了从定性到定量的集成评价，将现场监测数据纳入风险评价体系来预测其变化趋势.本文研究方法在充分认识风险的本质和相互联系后，动态分析边坡系统的整体风险，提高了风险评价结果的时效性和可靠性，预测结果更加准确客观.
参考文献(References)：
[1] 郑莲婧.金沙江旭龙水电站左岸坝肩边坡稳定分析评价 [D].长春：吉林大学，2015.
(ZHENG Lian-jing.The analysis of left bank dam abutment slope stability of Xulong hydropower station of Jinsha river [D].Changchun：Jilin Univerxity，2015.)
[2] Möller N，Hansson S O.Principles of engineering safety：risk and uncertainty reduction [J].Reliability Engineering & System Safety，2008，93(6)：798-805.
[3] 李典庆，肖特，曹子君，等.基于高效随机有限元法的边坡风险评估 [J].岩土力学，2016，37(7)：1994-2003.
(LI Dian-qing，XIAO Te，CAO Zi-jun，et al.Slope risk assessment using efficient random finite element method [J].Rock and Soil Mechanics，2016，37(7)：1994-2003.)
J
R，et al.Risk and reliability analysis of slope stability deterministic and probabilistic method[C]//17th International Research Expert Conference on Trends in the Development of Machinery and Associated Technology.Istanbul，Turkey，2013：229-232.
[5] Penna A，Lagomarsino S，Galasco A.A nonlinear macroelement model for the seismic analysis of masonry buildings [J].Earthquake Engineering and Structural Dynamics，2014，43(2)：159-179.
[6] Zhu H，Zhang L M.Evaluating suction profile in a vegetated slope considering uncertainty in transpiration [J].Computers and Geotechnics，2015，63(26)：112-120.
[7] 蔡文，杨春燕，林伟初.可拓工程方法 [M].北京：科学出版社，1997.
(CAI Wen，YANG Chun-yan，LIN Wei-chu.Extension engineering method [M].Beijing：Science Press，1997.)
[8] Saravanakumar R，Ali M S.Robust H∞control for uncertain Markovian jump systems with mixed delays [J].Chinese Physics B，2016，25(7)：108-113.
[9] 林登科，沈斐敏，廖素娟.基于可拓理论与区间赋权的煤矿水害安全评价 [J].安全与环境工程，2015，22(2)：124-128.
(LIN Deng-ke，SHEN Fei-min，LIAO Su-juan.Research on safety evaluation of coal mine water hazard based on extension theory and interval empowerment [J].Safety and Environmental Engineering，2015，22(2)：124-128.)
[10]赵博，徐卫亚，张冬梅，等.基于安全监测信息的岩石高边坡稳定性评价 [J].沈阳工业大学学报，2014，36(1)：100-105.
(ZHAO Bo，XU Wei-ya，ZHANG Dong-mei，et al.Stability evaluation of high rock slope based on safety monitoring information [J].Journal of Shenyang University of Technology，2014，36(1)：100-105.)
[11]周惠成，张改红，王国利.基于熵权的水库防洪调度多目标决策方法及应用 [J].水利学报，2007，38(1)：100-106.
(ZHOU Hui-cheng，ZHANG Gai-hong，WANG Guo-li.Multi-objective decision making approach based on entropy weights for reservoir flood control operation [J].Journal of Hydraulic Engineering，2007，38(1)：100-106.)
[12]周佳宽，郑博宁，赵红泽.基于熵权
可拓理论的边坡稳定性评价 [J].露天采矿技术，2016，31(7)：26-30.
(ZHOU Jia-kuan，ZHENG Bo-ning，ZHAO Hong-ze.Slope stability evaluation based on the extension theory combined with entropy weight [J].Opencast Mi-ning Technology，2016，31(7)：26-30.)
[13]Desharnais J，Edalat A，Panangaden P.Bisimulation for labelled Markov processes [J].Information & Computation，2015，179(2)：149-158.