电机驱动系统是电动汽车三大关键技术之一,无论是混合动力汽车、燃料电池汽车还是纯电动汽车,都离不开对电机驱动及控制系统的依赖[1].与用于其它类型电动汽车动力系统的电机相比,永磁同步电机具有高能量密度、高效率、易维护等优点,且目前电动汽车用永磁同步电机(PMSM)驱动系统普遍采用矢量控制技术和直接转矩控制技术.对于高性能的电动汽车电机驱动系统,最大转矩电流比(MTPA)控制、弱磁(FW)控制及电压与电流的限制是很重要的,直接转矩控制(DTC)系统可以利用基于运行条件所提供的参考转矩和参考磁链来实现最佳控制.然而,在大多数情况下,DTC系统需要利用与转子磁链同步旋转dq参考系中数学模型的控制规律[2],因此,需要计算d轴和q轴电流以确定转矩和磁通之间的关系,而且对电机参数依赖性大.为了解决传统DTC技术在电动汽车动力系统应用中所存在的低速转矩脉动及该动力系统对恒功率调速范围要求较高的问题,文献[3]提出了一种DSVM-DTC改进策略,通过优化低速区的开关表减小了低速转矩脉动,但低速转矩脉动减小的程度并不明显;文献[4]提出了基于龙贝格观测器的弱磁控制方法,其充分利用了母线电压,但弱磁控制算法较复杂,实现较困难,调速效果并不理想.
针对上述问题,本文提出了一种新型的永磁同步电机MT坐标系下的直接转矩控制系统.该系统中包括用于计算给定磁链的改进式MTPA控制和实现宽调速运行的弱磁控制,通过对定子磁链控制器所产生的磁链误差进行积分实现磁链估算.此外,传统的磁链估算方法没有考虑到逆变器所产生的电压饱和,降低了定子磁链的估算精度.在所提出的系统中,采用不同的电压矢量对所估算的磁链进行精确补偿,改善了系统所存在的低速转矩脉动,达到了宽速范围运行的目的.
1 永磁同步电机数学模型
PMSM驱动系统经常利用dq坐标系下的电机数学模型,其电压方程为
Ud=(Ra+PLd)id-wrLqiq
(1)
Uq=(Ra+PLq)iq+wrLdid+wrψa
(2)
式中:Ud与Uq分别为电枢电压的d轴和q轴分量;id与iq分别为电枢电流的d轴和q轴分量;Ld与Lq分别为电感的直轴分量和交轴分量;Ra为电枢电阻;wr为转子的角速度;ψa为永磁体磁链;P为微分算子.
然而,在本文所提出的系统中,PMSM驱动系统利用的是PMSM在MT坐标系下的电机数学模型,其电压方程[5-6]为
(3)
UT=RaiT+wsψs
(4)
式中:UM和UT分别为电枢电压矢量的M轴和T轴分量;iM和iT分别为电枢电流矢量的M轴和T轴分量;ψs为定子磁链矢量的幅值;ws为定子磁链矢量的角速度.
由于定子磁链矢量仅具有沿着M轴的分量,所以通过磁链和电流之间的正交关系来计算电磁转矩Te,其计算公式为
Te=PnψsiT
(5)
式中,Pn为电机的极对数.
定子磁链、电枢电流及电枢电压的坐标轴与矢量图如图1所示,图1中的αβ坐标系是静止参考坐标系,而MT坐标系是与定子磁链矢量同步旋转的参考坐标系,θs为定子磁链矢量的位置[7-8].
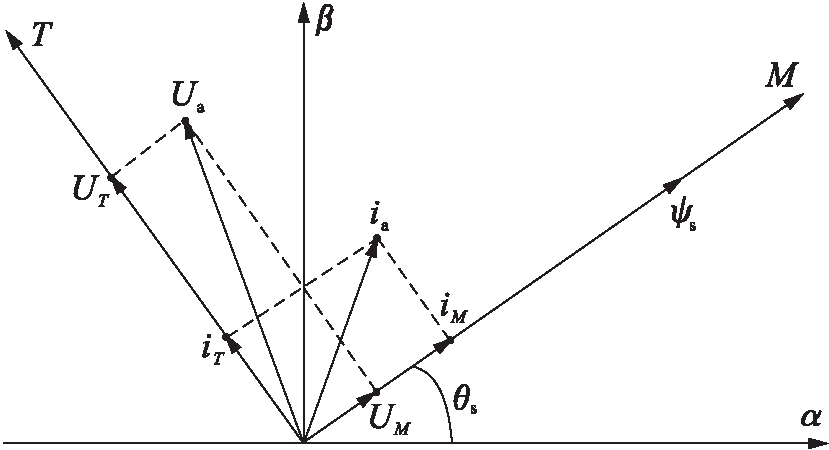
图1 系统坐标轴和稳态矢量图
Fig.1 Coordinate axes of system andvector diagram in steady state
2 MT坐标系下PMSM DTC控制系统
2.1 参考转矩与参考磁链的计算
本文所设计的参考转矩和参考磁链计算框图如图2所示.
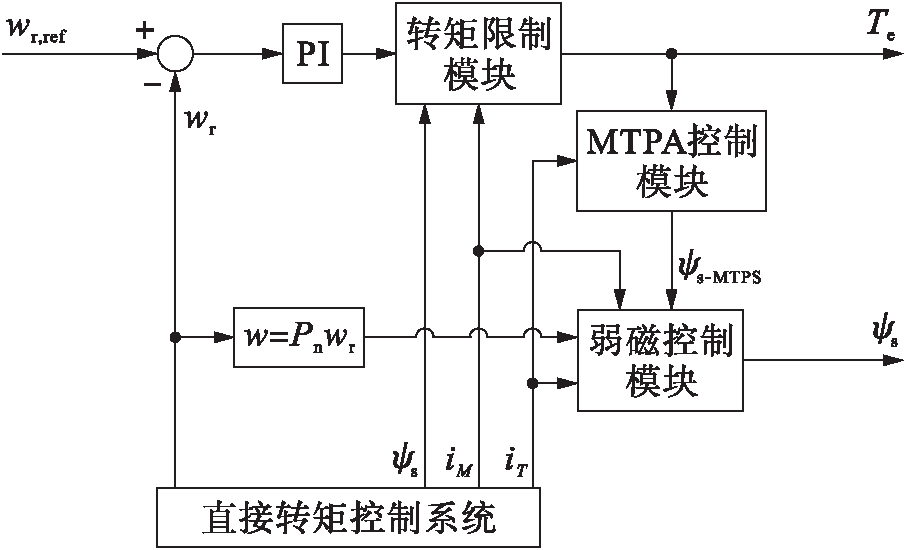
图2 参考转矩和参考磁链计算框图
Fig.2 Block diagram of calculating referencetorque and reference flux linkage
2.1.1 改进的MTPA控制
在传统PMSM的DTC控制系统中,转矩和磁链的参考值是根据dq坐标系中的数学模型计算出来的,然而在本文所提出的系统中,MTPA控制采用的数学模型为
![]() ψa
ψa
(6)
式中,b,L和Lk为常数,它们是根据电机的MTPA特性计算得到的.
在所提出的DTC控制系统中,根据转矩的参考值计算出磁链的参考值,但式(6)是关于电枢电流T轴电流分量的函数,因此,利用式(5)把转矩的参考值转换为电枢电流T轴电流分量值.利用MTPA控制计算参考磁链值的关系框图如图3所示,该方法使得电枢电流T轴分量值达到MTPA控制的工作点,当iT=iT1时,磁链的参考值也达到MTPA控制的最佳值[9].
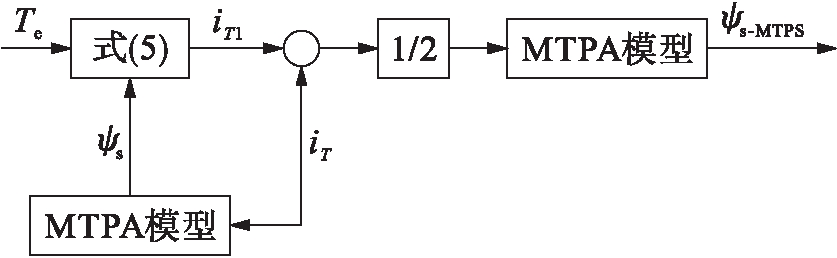
图3 MTPA算法计算参考磁链
Fig.3 Calculation of reference flux linkagewith MTPA algorithm
2.1.2 弱磁控制
与传统dq坐标系下的控制方法相比,由于DTC系统直接控制定子磁链变量,所以DTC系统更容易完成弱磁控制[8-11].在本文所提出的控制系统中,当系统处于高速运行区域时,通过弱磁控制使得电枢电压达到极限值,且弱磁控制方法的数学模型是从MT坐标系下电压方程推导出来的,将![]() 代入到式(4)中,便可以得到定子磁链的动态幅值,弱磁控制的数学模型[12]为
代入到式(4)中,便可以得到定子磁链的动态幅值,弱磁控制的数学模型[12]为
(7)
式中,Uam为电枢电压的极限值.
2.1.3 转矩限制器
由于电枢电流的实际值是由逆变器和电机的容量确定的,且存在极限值,从而对转矩的幅值产生了一定的限制作用.对于永磁同步电机而言,可以利用磁阻转矩,但该转矩和电流的关系是非线性的,因此推导出这种关系是非常复杂的.在所提出的系统中,转矩限制器则利用式(5)作为数学模型进行转矩限制值计算,其模型表达式为
Tm=PnψsiTm
(8)
式中,iTm为电枢电流T轴分量的极限值.
当电枢电流达到极限值iam时,电枢电流T轴分量的极限值计算公式为
(9)
因此,转矩限制器的控制规则可以由式(8)、(9)得到,且转矩限制值可以表示为
(10)
2.2 MT坐标系下的DTC系统
MT坐标系下的DTC系统框图如图4所示,该系统的转矩控制器采用比例、积分(PI)控制器,由于具有相同的转矩控制原理,所以可以采用文献[13]中所描述的增益设计方法,转矩控制器的增益可以表示为
![]() ζwn
ζwn
(11)
(12)
式中:kP和ki分别为比例增益和积分增益;ts为采样周期;ζ为阻尼因子;wn为自然角频率;kT为转矩关于转矩角的导数.
在所提出的DTC控制系统中,定子磁链矢量的角速度估计值是通过定子磁链角位置变化量的参考值获得的;定子磁链的角位置估计值是通过对定子磁链矢量的角速度估计值进行积分得到的,它被用于进行坐标变换;磁链的估计值是通过磁链偏差积分得到的,并且对磁链进行前馈控制.另一方面,本文所提出的控制器是采用PMSM的 离散模型进行构建的,其中的感应电压Uo与式(3)右侧第二项相对应,且需要进行离散化处理.感应电压矢量与定子磁链矢量的关系示意图如图5所示,由于定子磁链变化导致产生感应电压,其感应电压计算式为
(13)
式中:k为当前数值;k+1为下一个采样周期内的数值.
通过式(13)可以求出感应电压矢量的M轴与T轴电压分量的参考值[14-15],其计算公式为
![]() ψs+Δψs)cos Δ
ψs+Δψs)cos Δ![]() ψs]
ψs]
(14)
![]() ψs+Δψs)sin Δ
ψs+Δψs)sin Δ![]()
(15)
式中:Δ![]() 为定子磁链角度变化量的参考值;
为定子磁链角度变化量的参考值;![]() 和
和![]() 分别为感应电压矢量的M轴与T轴分量参考值.
分别为感应电压矢量的M轴与T轴分量参考值.
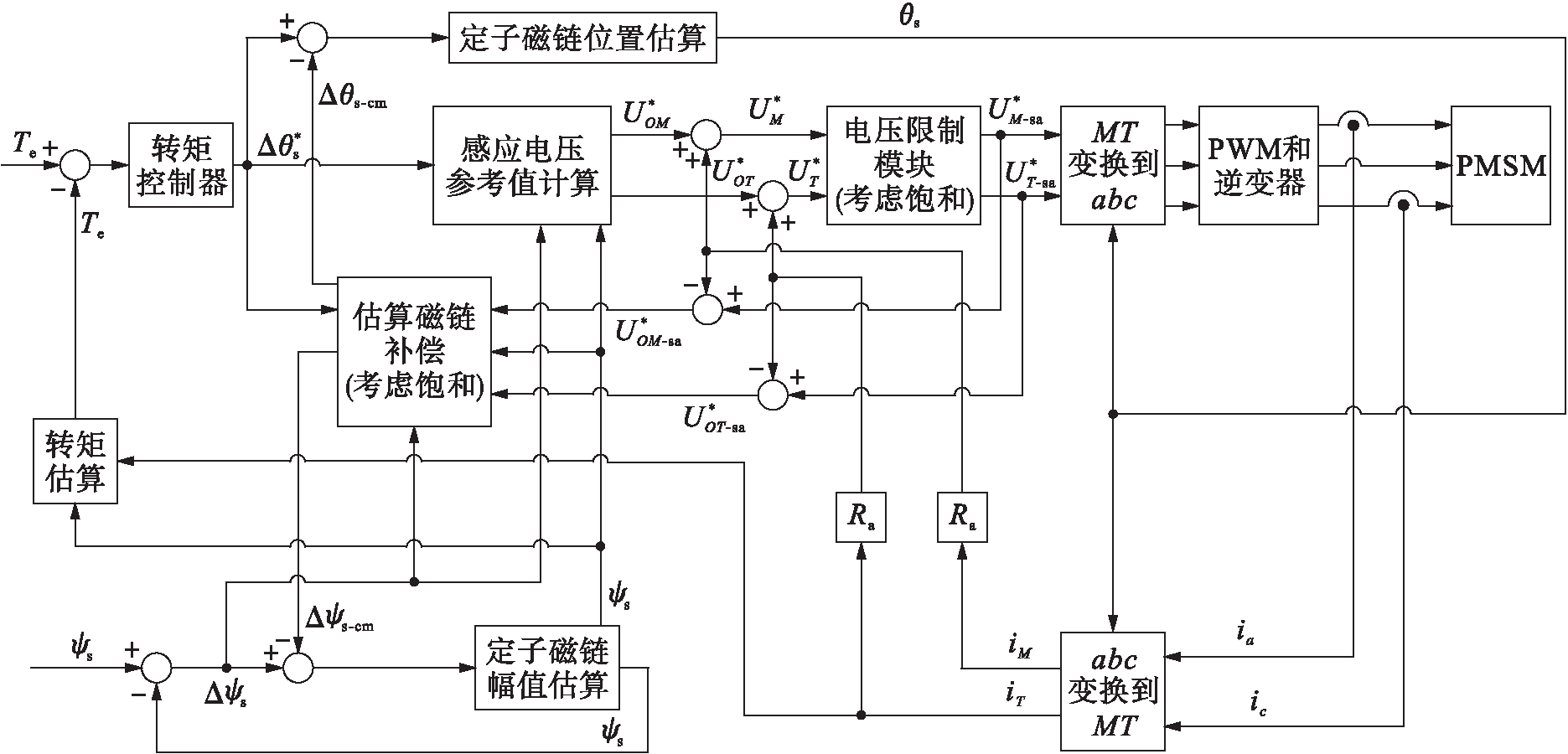
图4 MT坐标系下的DTC系统框图
Fig.4 Block diagram of DTC system in MT coordinate system
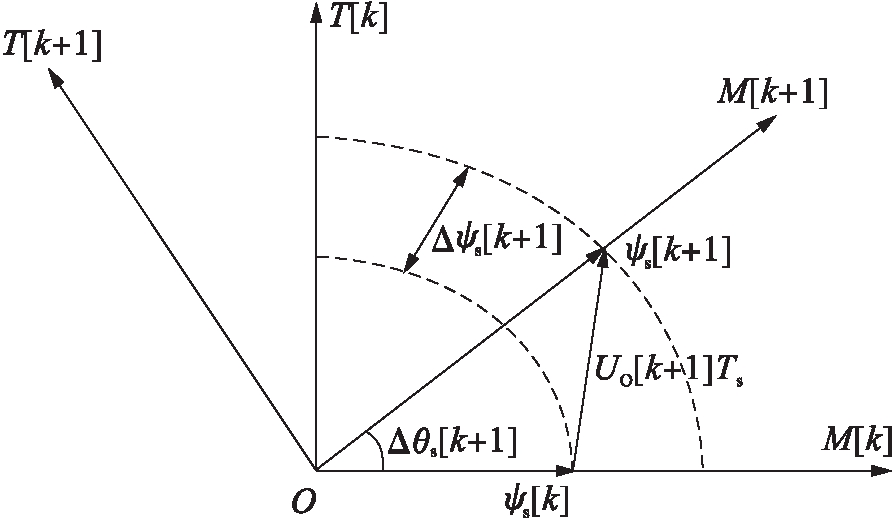
图5 离散时间条件下定子磁链矢量和电压矢量的关系
Fig.5 Relationship between stator flux linkage vector andvoltage vector under condition of discrete time
2.3 电压饱和条件下估算磁链补偿
MT坐标系下DTC系统所估计的定子磁链是通过磁链的误差量积分获得的,因此,电枢电压的饱和将会导致磁链估算的结果产生误差.当电枢电压达到饱和值时,即最大电压值Umax时,参考电枢电压矢量的变化曲线如图6所示,系统中电枢电压矢量的角度不发生改变.饱和电枢电压的M轴与T轴电压分量的参考值![]() 和
和![]() 计算公式为
计算公式为
(16)
(17)
式中,![]() 和
和![]() 分别为电枢电压矢量的M轴和T轴电压分量的参考值.
分别为电枢电压矢量的M轴和T轴电压分量的参考值.
由于感应电压的参考值![]() 和
和![]() 和饱和感应电压的参考值
和饱和感应电压的参考值![]() 和
和![]() 之间存在着一 定的差异,所以使得所估计的定子磁链产生了相应的误差,磁链的幅值误差和磁链的位置误差分别表示为
之间存在着一 定的差异,所以使得所估计的定子磁链产生了相应的误差,磁链的幅值误差和磁链的位置误差分别表示为
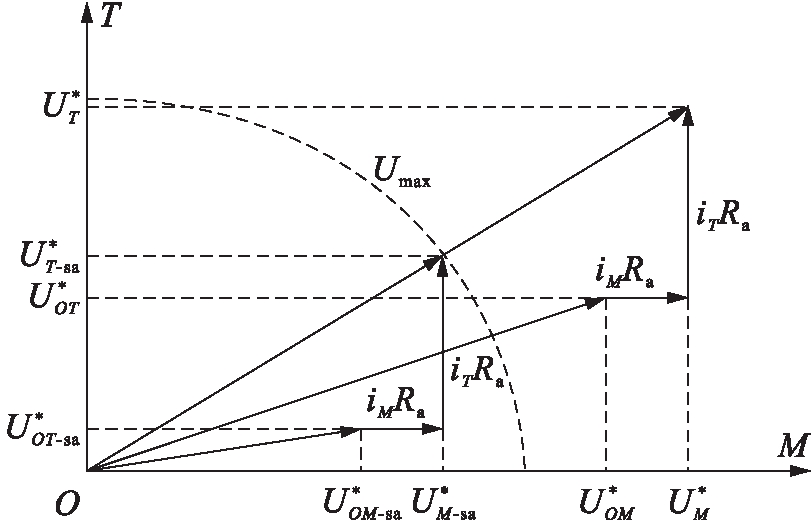
图6 当电枢电压达到饱和时电枢电压矢量的变化曲线
Fig.6 Change of armature voltage vector whenarmature voltage reaching saturation
Δψs-cm=ψs+Δ![]()
(18)
Δθs-cm=Δ![]()
(19)
式中,ψM和ψT分别为下一个采样周期内定子磁链矢量在M轴和T轴的分量,其计算表达式为
(20)
(21)
3 仿真结果与分析
本系统所采用的PMSM参数为:极对数为2,ψa=0.108 5 Wb,Ld=8.75 mH,Lq=28.35 mH,电枢电阻为0.64 Ω,转动惯量为0.002 kg·m2,电枢电流极限值为8.6 A,采样周期为100 μs;速度控制器:kp=0.04,ki=0.01;转矩控制器:kp=0.16,ki=30;电压限压器的最大电压(Umax)为93 V;弱磁控制模块的电枢电压极限值(Uam)为82.5 V.
仿真研究对比:
1) 参考转速设定为100 r/min,初始时刻负载转矩为TL=0 N·m,在t=0.2 s时突加负载转矩TL=1.5 N·m,对文献[3]提出的DSVM-DTC改进策略与MT坐标系下DTC策略的低速转矩脉动情况进行转速与转矩的仿真对比,结果如图7~10所示.
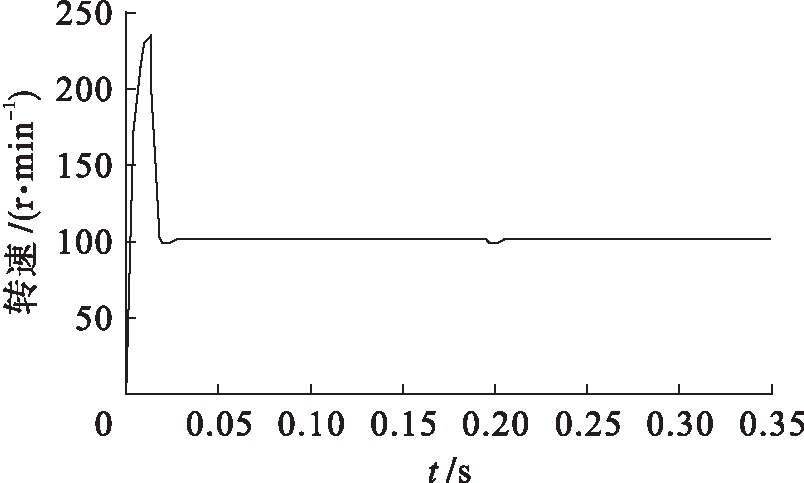
图7 DSVM-DTC的转速曲线
Fig.7 Rotating speed curve of DSVM-DTC
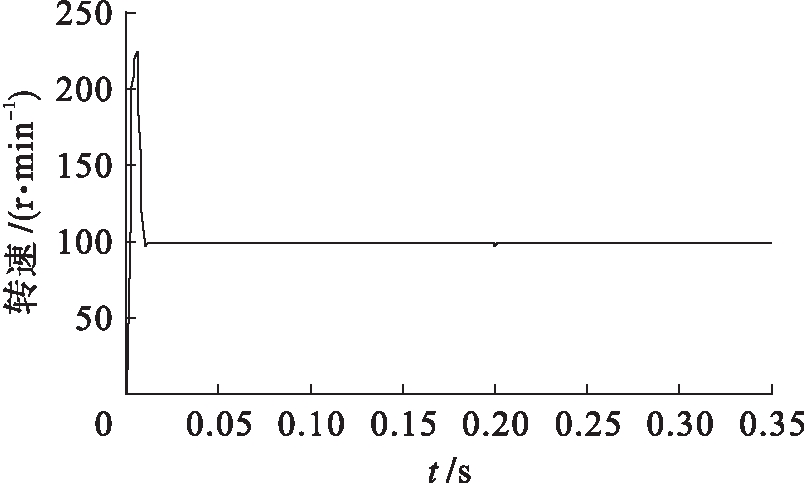
图8 MT坐标系下DTC的转速曲线
Fig.8 Rotating speed curve of DTCin MT coordinate system
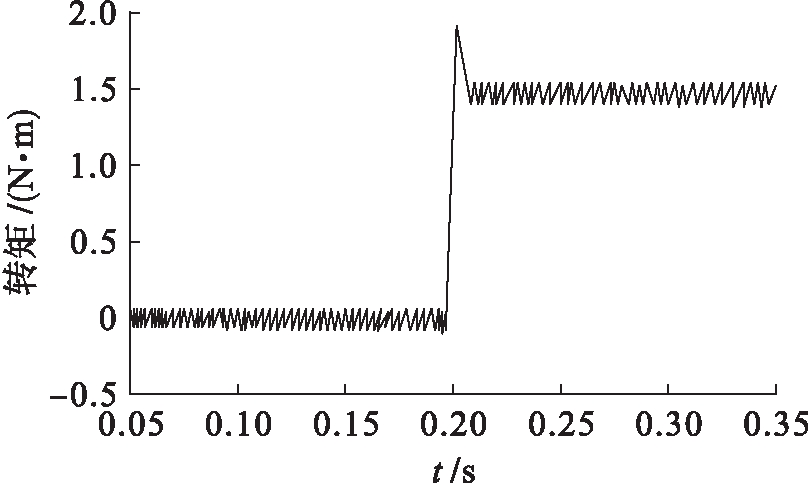
图9 DSVM-DTC的转矩曲线
Fig.9 Torque curve of DSVM-DTC
由图7、8的仿真结果可以看出,当电机从零速上升到参考转速100 r/min时,虽然开始时电机转速有一些超调量,但仍然具有较快的动态响应速度,并且当0.2 s突加负载转矩后,电机也能快速恢复到给定参考转速值;从图9、10仿真结果可以看出,文献[3]提出的DSVM-DTC改进策略的转矩 波动值为0.16 N·m,而本文所提出的MT坐标系下DTC控制策略的转矩波动值为0.04 N·m,转矩波动幅值显著减小,从而说明所提出的DTC系统可以更加有效地抑制低速转矩脉动,并且具有较好的动态性能和抗扰动能力.
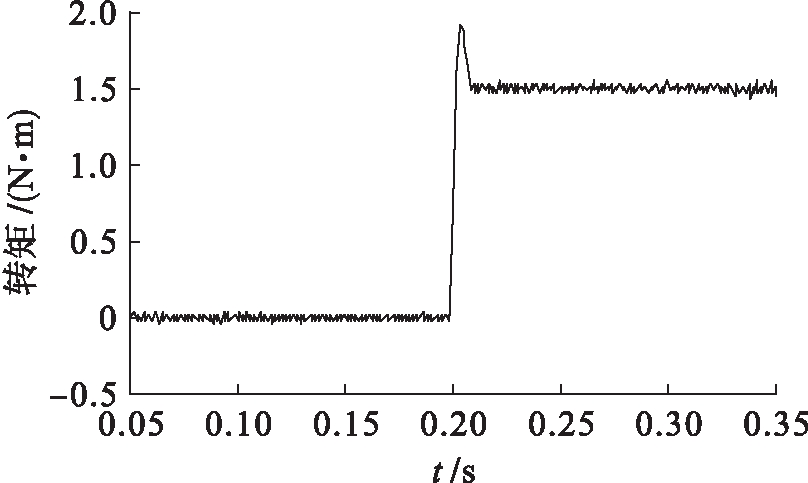
图10 MT坐标系下DTC的转矩曲线
Fig.10 Torque curve of DTC in MT coordinate system
2) 在空载条件下,设定参考转速在0.5 s时由100 r/min变为4 500 r/min,对MT坐标系下DTC系统的加速性能进行仿真研究,结果如图11~15所示.
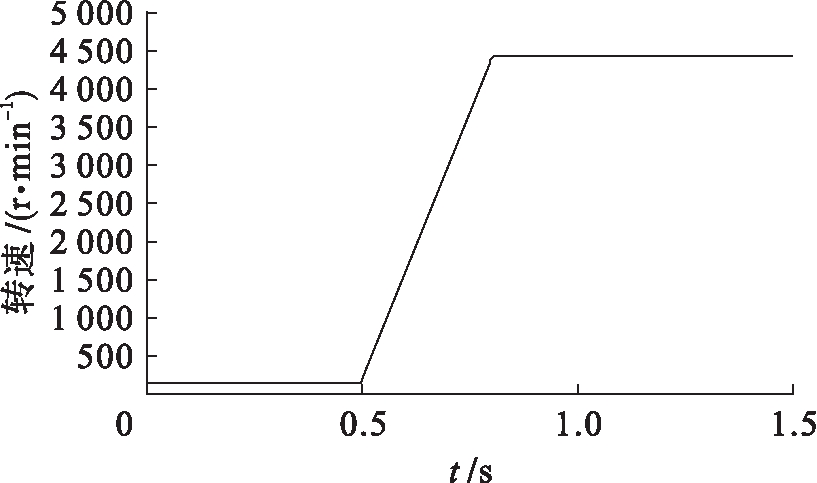
图11 转速曲线
Fig.11 Rotating speed curve
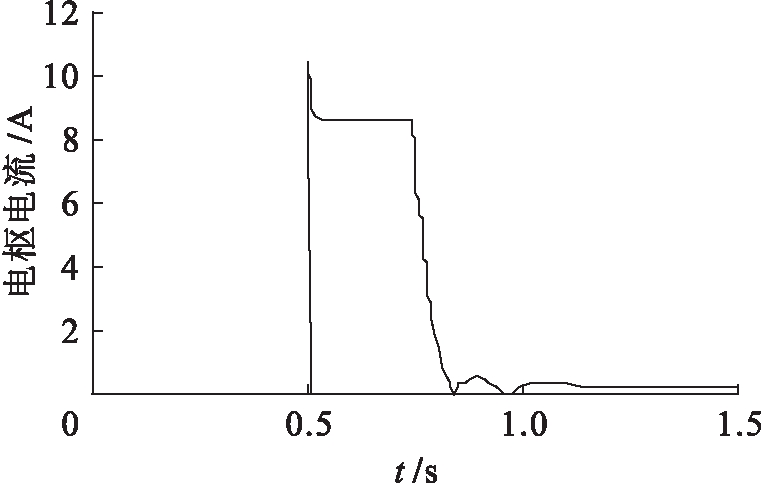
图12 电枢电流曲线
Fig.12 Armature current curve
由图11~15所示的仿真结果可以看出,在加速过程中,图11中电机的实际转子转速在0.5 s时,随着参考转速设定值的改变可以稳定地从100 r/min升至4 500 r/min.图12中电枢电流在参考转矩值增大之后发生巨大变化,电压出现饱和现象,但由于补偿环节对估算磁链的补偿作用,实现了对转矩和磁链的稳定控制,并且电枢电流值在加速期 间一直保持在8.6 A左右.图13、14中的转矩、磁链的估算值与参考值几乎接近,转矩与磁链在0.5 s时随着参考转速设定值的改变而迅速的增大,在100~3 000 r/min之间,转矩与磁链保持恒定不变;在3 000~4 500 r/min之间,转矩与磁链逐渐减小,二者最终趋于稳定.但转矩在0.5 s时,由于电压饱和对转矩控制器产生影响,从而出现转矩值过大的现象.图15中M轴和T轴电流在恒转矩运行区域,保持常数不变,M轴电流随着转速的增加而减小,T轴电流则随着转速的增加而增加.
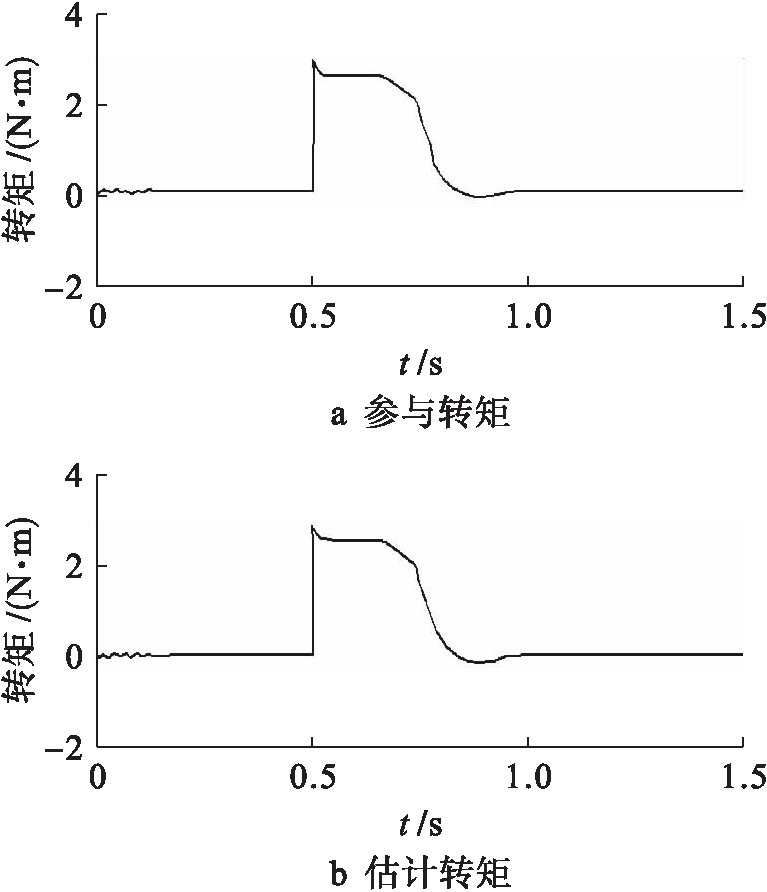
图13 转矩曲线
Fig. 13 Torque curve
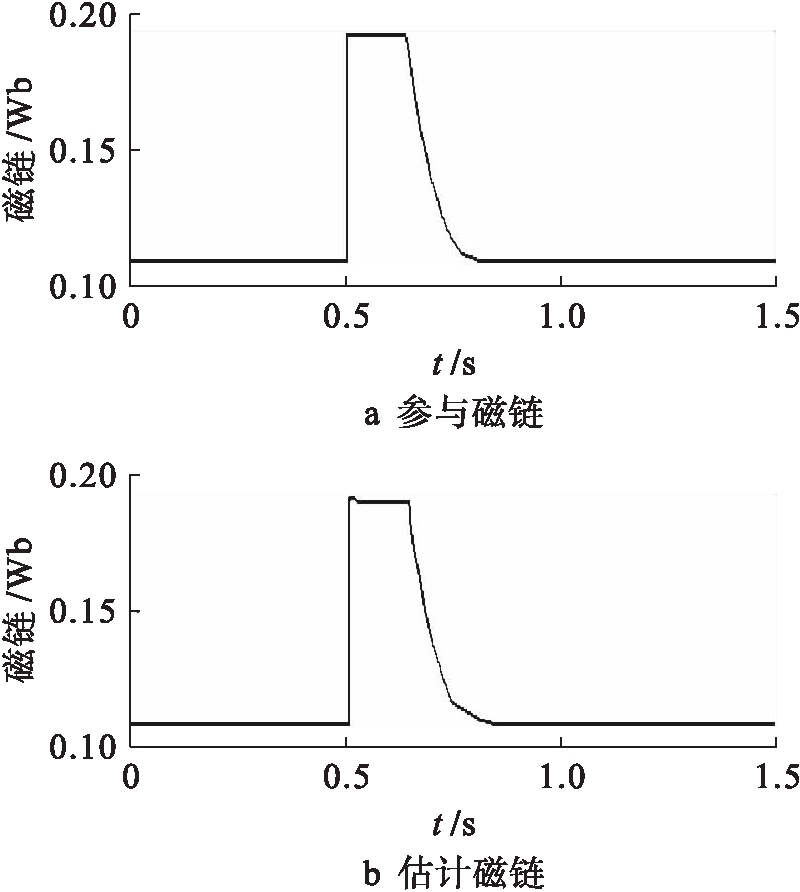
图14 定子磁链曲线
Fig. 14 Stator flux linkage curve
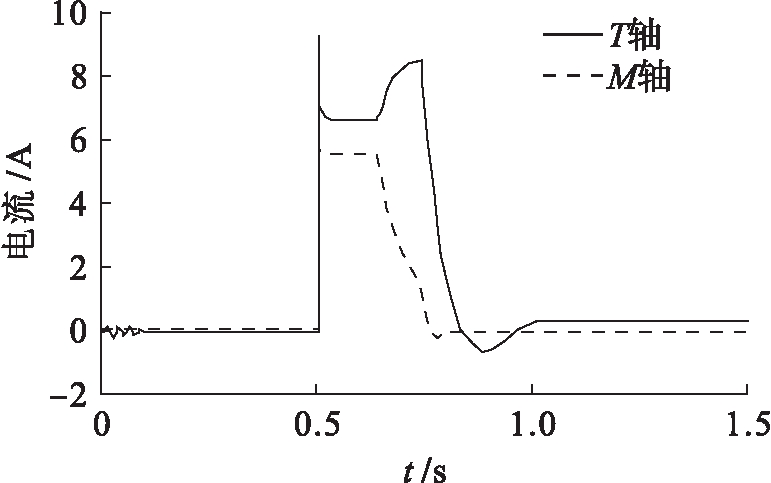
图15 M轴与T轴电流曲线
Fig. 15 Current curves of M and T axes
综上所述,所提出的DTC系统在恒转矩运行区域时,采用MTPA控制以产生最大转矩;在恒功率运行区域时,相比采用文献[4]所提出的基于龙贝格观测器的弱磁方法,本系统所采用的弱磁方法简单、易于实现,且调速范围得到了拓宽,使得电机可以在高速时稳定运行.
4 结 论
针对直接转矩驱动技术在电动汽车动力系统应用中所存在的低速转矩脉动以及动力系统对恒功率调速范围要求较高的问题,提出了一种新型永磁同步电机MT坐标系下的直接转矩控制系统.该系统采用改进MTPA控制计算给定磁链,采用弱磁控制实现宽速范围运行,通过对定子磁链控制器所产生的磁链误差进行积分实现磁链估算.此外,传统磁链估算方法没有考虑到逆变器所产生的电压饱和,降低了定子磁链的估算精度,本系统则采用了不同的电压矢量对所估算的磁链进行精确补偿,进而改善了系统存在的低速转矩脉动问题,并实现了宽调速范围运行.
参考文献(References):
[1] 张红伟.新能源汽车的发展现状及前景分析 [J].汽车实用技术,2016(9):22-24.
(ZHANG Hong-wei.Analysis of development status and prospect of new energy vehicles [J].Automobile Applied Technology,2016(9):22-24.)
[2] Zhang Y,Zhu J,Xu W,et al.A simple method to reduce torque ripple in direct torque controlled permanent magnet synchronous motor by using vectors with variable amplitude and angle [J].IEEE Transactions on Industrial Electronics,2011,58(7):2848-2859.
[3] 胡卫华,奚国华,喻寿益,等.一种改善直接转矩控制低速性能的DSVM改进策略 [J].电气传动,2007,37(9):11-14.
(HU Wei-hua,XI Guo-hua,YU Shou-yi,et al.Improved DSVM strategy to modify the low speed performance of direct torque control [J].Electric Drive,2007,37(9):11-14.)
[4] 陈宁,张跃,桂卫华,等.变频空调驱动电机的弱磁控制 [J].电机与控制学报,2014,18(7):65-71.
(CHEN Ning,ZHANG Yue,GUI Wei-hua,et al.Flux weakening control for drive motor of inverter air conditioner [J].Electric Machines and Control,2014,18(7):65-71.)
[5] 陈志锦,马艳.永磁同步电机参数自动辨识方法研究 [J].电子设计工程,2016,24(4):144-147.
(CHEN Zhi-jin,MA Yan.Research on parameter automatic identification of PMSM [J].Electronic Design Engineering,2016,24(4):144-147.)
[6] Pellegrino G,Bojoi R I,Guglielmi P.Unified direct-flux vector control for AC motor drives [J].IEEE Transactions on Industry Applications,2011,47(5):2093-2102.
[7] Inoue Y,Ichiya T,Morimoto S,et al.Wide-speed-range operation of DTC based PMSM drive system using MTPF control [C]//2014 International Power Electronics Conference.Hiroshima,Japan,2014:370-375.
[8] 钱伟康,郭论,洪晨,等.基于EPS的永磁同步电机弱磁控制仿真研究 [J].电子科技,2017,30(1):111-114.
(QIAN Wei-kang,GUO Lun,HONG Chen,et al.Simulation research on flux weakening control of permanent magnet synchronous motor based on EPS [J].Electronic Science and Technology,2017,30(1):111-114.)
[9] Inoue T,Inoue Y,Morimoto S,et al.Mathematical model for high efficiency control of permanent magnet synchronous motor in stator flux linkage synchronous frame [C]//2014 International Power Electronics Conference.Hiroshima,Japan,2014:363-369.
[10]史宇超,孙凯,黄立培,等.内埋式永磁同步电机宽调速范围运行控制策略 [J].清华大学学报(自然科学版),2012,52(11):1565-1570.
(SHI Yu-chao,SUN Kai,HUANG Li-pei,et al.Control of interior permanent magnet synchronous motor drives over a wide speed range [J].Journal of Tsinghua University (Science and Technology),2012,52(11):1565-1570.)
[11]庄见伟,房绪鹏,李辉.基于非正交坐标系下模糊PI永磁同步电机的研究 [J].现代电子技术,2016,39(11):164-167.
(ZHUANG Jian-wei,FANG Xu-peng,LI Hui.Study on PMSM with fuzzy PI controller based on no orthogonal coordinate system [J].Modern Electronics Technique,2016,39(11):164-167.)
[12]Inoue Y,Morimoto S,Sanada M.Comparative study of PMSM drive systems based on current control and direct torque control in flux-weakening control region [J].IEEE Transactions on Industry Applications,2012,48(6):2382-2389.
[13]Inoue Y,Morimoto S,Sanada M.Examination and linearization of torque control system for direct torque controlled IPMSM [J].IEEE Transactions on Industry Applications,2010,46(1):159-166.
[14]Tang L,Zhong L,Rahman M F,et al.A novel direct torque control for interior permanent-magnet synchronous machine drive with low ripple in torque and flux-a speed-sensorless approach [J].IEEE Transactions on Industry Applications,2003,39(6):1748-1756.
[15]Choi C H,Seok J K,Lorenz R D.Wide-speed direct torque and flux control for interior PM synchronous motors operating at voltage and current limits [J].IEEE Transactions on Industry Applications,2013,49(1):109-117.