绝热剪切带是在高应变速率荷载条件下材料所产生的一种独特的失效形式，普遍存在于高速冲击、冲孔、冲蚀、切削等高速变形过程中[1-2].在高速变形过程中，材料应变能的90%将转化为内能，加之转变过程极为短暂，从而会导致材料自身温度急剧升高且来不及散失.因此，可以认为上述高速变形过程为绝热升温过程.作为一种特殊的材料局部失稳形式的标志，绝热剪切带的出现表征材料承载力水平的降低甚至失效[3].目前，有关绝热剪切带的研究所用冲击试样大多是柱状或块状的，但由于帽状试样结构更有利于在加载后处于纯剪切状态而更适于获取绝热剪切带[4]，因此，帽状试样被广泛应用于高速冲击变形组织的研究领域.
随着汽车工业的蓬勃发展，其带来的环境问题日益严重，汽车自身减重问题受到了广泛的关注和研究，采用镁合金和铝合金来代替钢铁已成为当今汽车减重降排的发展趋势.因此，通过研究镁合金和铝合金的动态力学性能从而提高汽车的安全性显得愈加重要[5-9].在模拟材料动态力学性能方面，相关学者提出的经验材料本构模型[10-12]已经成为采用有限元方法进行精确性计算的有力工具，同时该模型也使得材料本构方程的参数拟合更加简单.
传统科学分析方法仅限于观察材料变形前后的组织变化，并通过材料所表现出来的力学性能对材料的变形过程进行分析.数值模拟方法则可以更好地再现材料的变形过程.魏志刚等[13]利用ABAQUS软件对钨合金材料的绝热剪切机理进行研究后发现，在一维应力冲击条件下钨合金圆柱状试样变形均匀，且很难观察到微裂纹、微孔洞和绝热剪切带，而哑铃形和阶梯形试样在受到很小的冲击下，即可观察到绝热剪切带；李建崇等[14]利用LS-DYNA软件对TC4合金的动态剪切过程进行了数值模拟后发现，在冲击载荷作用下TC4合金绝热剪切带的内部温度达到了TC4合金的再结晶温度，该发现为TC4合金内部微观组织变形机制的研究提供了理论依据.然而，目前针对镁合金和铝合金动态压缩行为数值模拟的相关研究仍然较为欠缺，本文利用ANSYS/LS-DYNA软件分别对AZ31B镁合金和6065铝合金帽状试样的动态压缩过程进行了数值模拟，对比了在高应变率压缩条件下两种合金的变形特点，以期为两种合金的工程应用提供相关参考.
1 实验模型
1.1 本构模型与损伤方程
Johnson-Cook本构方程能够以非耦合形式同时考虑应变硬化、应变率敏感性和热软化作用的影响，其一般表达式为
·
(1)
式中：
为等效应力；εp1为等效塑性应变；
为等效塑性应变率；
为相对应变率，一般取
10-3 s-1；TM为金属熔点；T0为参考温度；T为材料自身温度；A、B、n、C和q分别为材料的屈服强度、硬化系数、硬化指数、应变率敏感指数与温度软化指数.当T=T0时，该本构方程为等效应力与等效塑性应变之间的函数关系；当T>T0时，该本构方程为等效应力、等效塑性应变和温度之间的函数关系.
为了进一步描述材料累积损伤时的本构关系，Johnson-Cook提出了新的模型，其表达式为
εf= [D1+D2exp(D3σ*
·
(2)
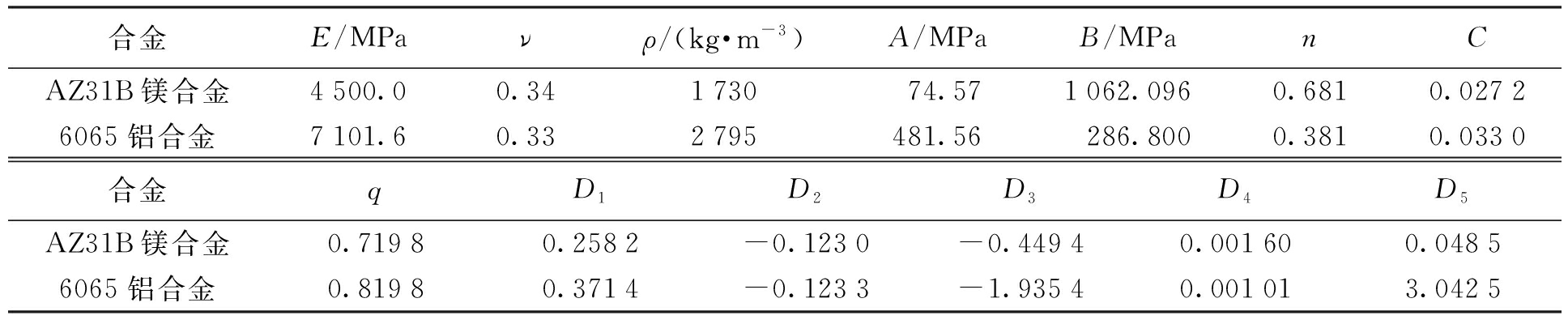
式中：εf为损伤塑性应变；σ*为三向应力值；D1、D2、D3、D4和D5为累积损伤模型中的相应损伤常数.AZ31B镁合金和6065铝合金的材料属性如表1所示，其中E、ρ和ν分别为合金的弹性模量、密度与泊松比.
表1 合金的材料属性
Tab.1 Material properties of alloys
1.2 有限元模型
基于分离式霍普金森压杆系统进行高速冲击实验，SHPB系统尺寸与材料属性分别如表2、3所示.
为了提高计算精度并节省计算时间，本文采用了二维轴对称模型.为了易于捕捉到绝热剪切带，本文采用帽状试样，其具体尺寸如图1所示 (单位：mm).由于帽状试样在变形过程中可能会在试样的两个拐角连线处产生强烈的局域化变形带，因此，对该区域进行了网格细化处理.SHPB系统的有限元模型如图2所示，其中网格细化区域范围为10 μm×10 μm，单元总数量为8 674个.在实验过程中子弹首先撞击输入杆(红色部分)，并将能量通过输入杆传递到帽状试样(绿色部分)，再由帽状试样将能量进一步传递到输出杆(蓝色部分)，同时在输出杆的一端产生反射能量，最后经过试样反射返回至输入杆，其整个过程遵循一维弹性波理论.
表2 SHPB系统尺寸
Tab.2 Size of SHPB system mm
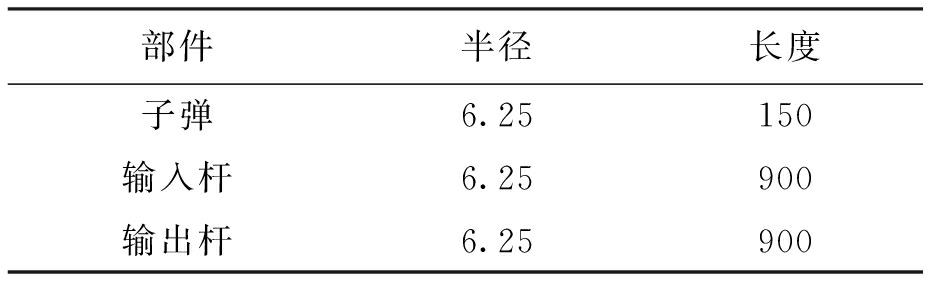
表3 结构钢的材料属性
Tab.3 Material properties of structural steel
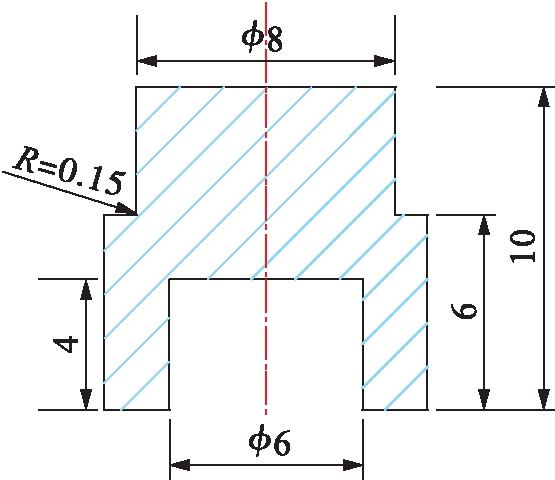
图1 帽状试样的几何尺寸
Fig.1 Geometric size of hat-shaped specimen
图2 SHPB系统的有限元模型
Fig.2 Finite element model for SHPB system
本文采用Automatic 2D Single Surface Contact接触方式.子弹初速度为13 m/s，试样初始温度为300 K.完成有限元模型建立和边界条件施加后，输出Key文件，并添加表1、2所示的热物性参数，进而求解两种合金在热力耦合条件下的本构关系.
2 分析与讨论
2.1 裂纹的萌生与扩展
利用LS-PREPOST软件提取实体模型数值模拟结果，从而再现子弹冲击后的帽状试样动态变形过程.图3为当子弹速度为13 m/s时，AZ31B镁合金帽状试样塑性应变过程的数值模拟结果.帽状试样的几何不连续性导致高塑性应变区域首先产生于帽状试样的两拐角连线处，当塑性应变累积量超过损伤判定值时，帽状试样两拐角连线处将会萌生裂纹.随着载荷的增加，高塑性应变区域向两拐角连线的中间区域处进行扩展与汇聚的同时，裂纹也向该中间区域进行延伸，直至帽状试样发生完全断裂.
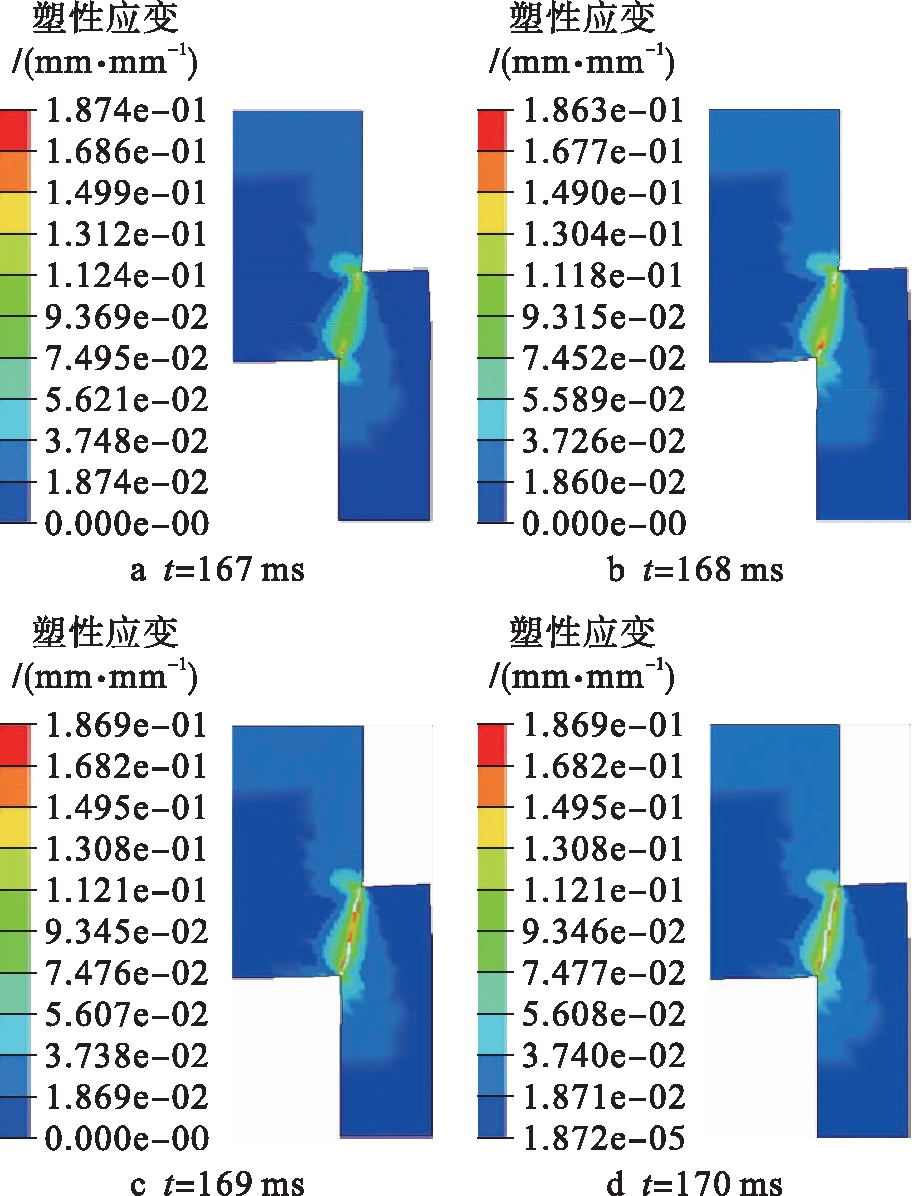
图3 AZ31B镁合金塑性应变过程的数值模拟
Fig.3 Numerical simulation for plastic strainprocess of AZ31B magnesium alloy
相同实验条件下6065铝合金帽状试样塑性应变过程的数值模拟结果如图4所示.与AZ31镁合金帽状试样的塑性应变过程相比，6065铝合金的高塑性应变区域和裂纹的扩展方式较为一致，且其扩展速度高于AZ31B镁合金，但6065铝合金的塑性影响区域更加细长而狭窄，同时6065铝合金的损伤塑性应变临界值高于AZ31镁合金.
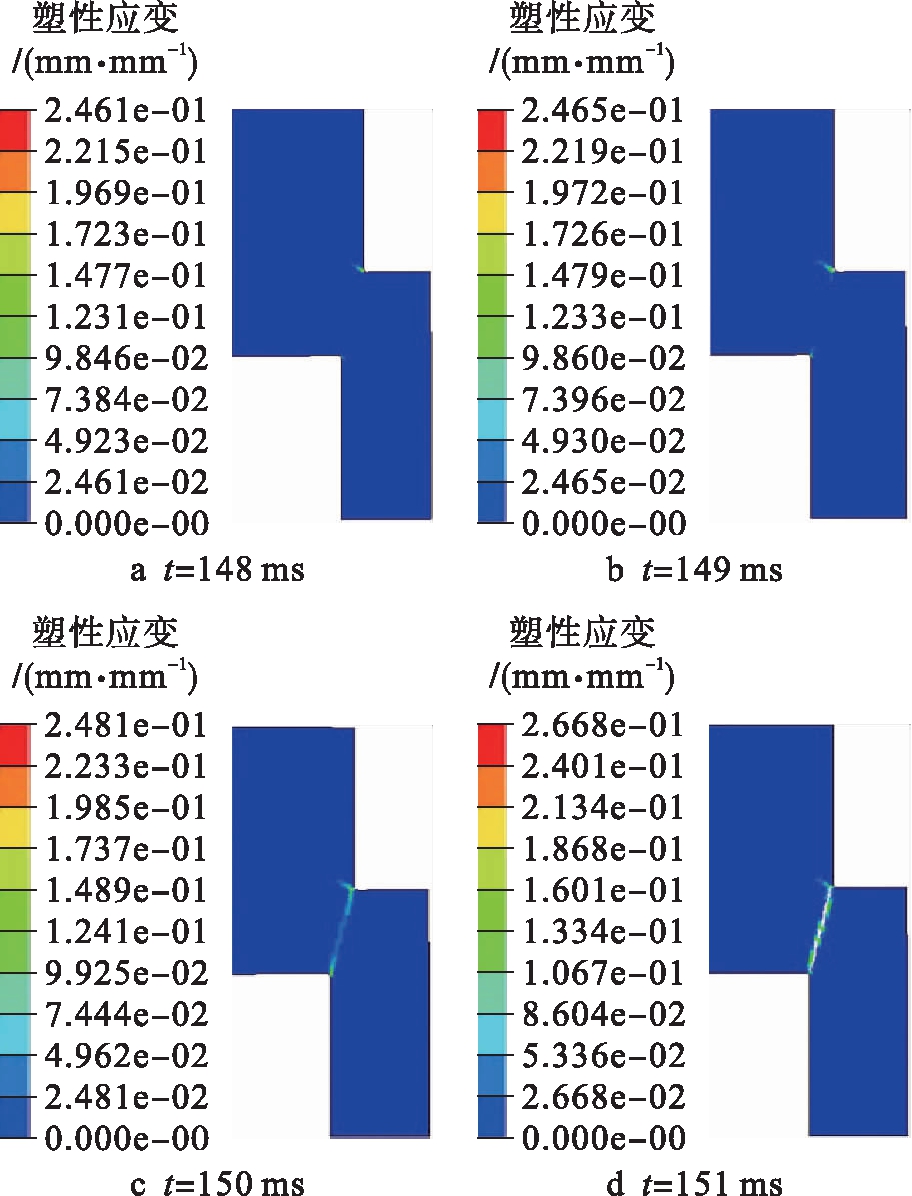
图4 6065铝合金塑性应变过程的数值模拟
Fig.4 Numerical simulation for plastic strainprocess of 6065 aluminum alloy
2.2 变形温度分析
在高应变速率条件下绝热剪切带通常被认为是材料的一种失效形式.由于局域化变形在较高的温度条件下会形成绝热剪切带，因此，温度是衡量绝热剪切带形成的重要因素.温升转变关系的一般表达式为
Δ
εp1
(3)
式中：εt为最后时刻的塑性应变值；Cp为比热容；α为功热转换系数，且在高应速率条件下一般α=0.9.
图5为AZ31镁合金帽状试样在不同时刻的温度云图.由图5可见，试样温度呈层状分布，裂纹扩展前沿温度较高，且其分布形态与该合金的塑性应变云图类似，这主要是因为变形过程中温度来自塑性功的转变.
相同实验条件下6065铝合金帽状试样在不同时刻的温度云图如图6所示.由图6可见，6065铝合金的温度影响区域范围也与其塑性应变云图类似.值得注意的是，在子弹速度为13 m/s的室温条件下，AZ31B镁合金试样的最大温升为588.3 K，该数值低于AZ31镁合金的动态再结晶温度，这与Rittel等[15]研究得到的AM50合金试 样内部最高温度为533 K的实验结果相接近.然而，6065铝合金试样的最大温升能够达到671 K，该数值高于6065铝合金的动态再结晶温度，这与Wang等[16]研究得到的6061合金剪切带内温度能够达到667 K的实验结果相接近.可见，与AZ31镁合金相比，6065铝合金更易形成绝热剪切带.
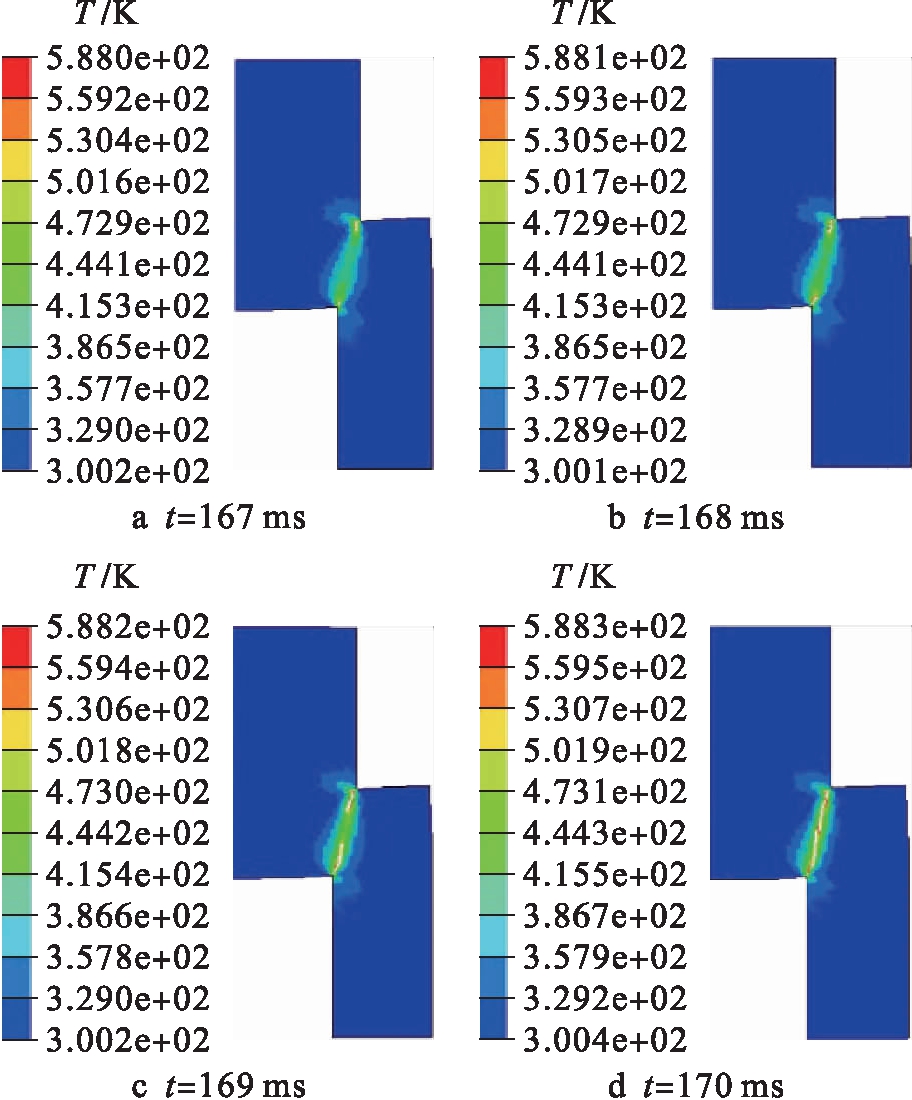
图5 AZ31B镁合金的温度云图
Fig.5 Temperature nephogram ofAZ31B magnesium alloy
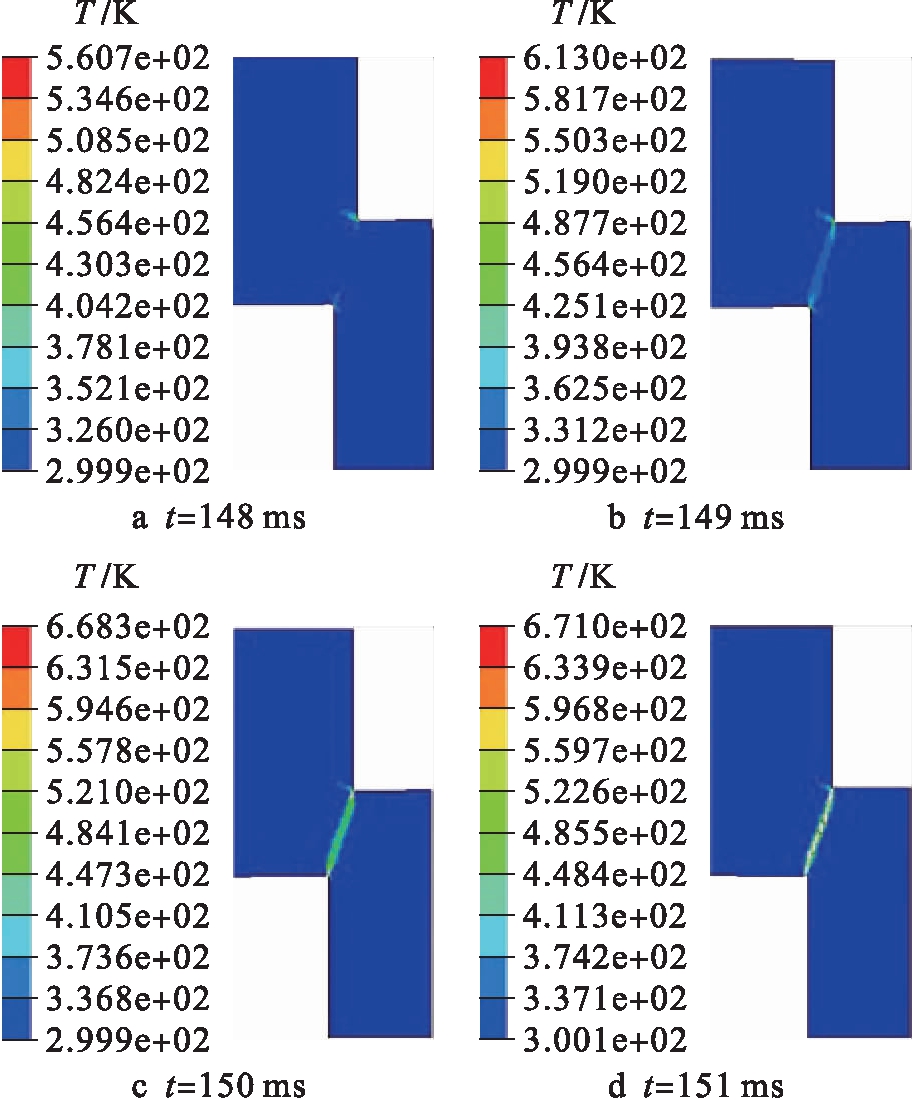
图6 6065铝合金的温度云图
Fig.6 Temperature nephogram of6065 aluminum alloy
2.3 局域化变形带内应力应变关系
在高应变速率条件下帽状试样在变形过程中存在两种形式，分别为由应变和应变率导致的材料硬化以及由高应变率塑性功转变为内能引起的材料热软化.在应变和应变率硬化为主导的变形过程中，材料的自身承载能力会得到一定程度的提高，主要表现为应力增长速率大于塑性应变增长速率.然而，在热软化效应强于应变和应变率硬化的变形过程中，当内部温升较高时，材料将发生流变失稳，致使材料内部变形发生局域化并产生绝热失稳，从而形成了绝热剪切带，即材料产生“自锐”效应.在局域化变形带内部以及周围提取5个特征单元，其编号及位置如图7所示.
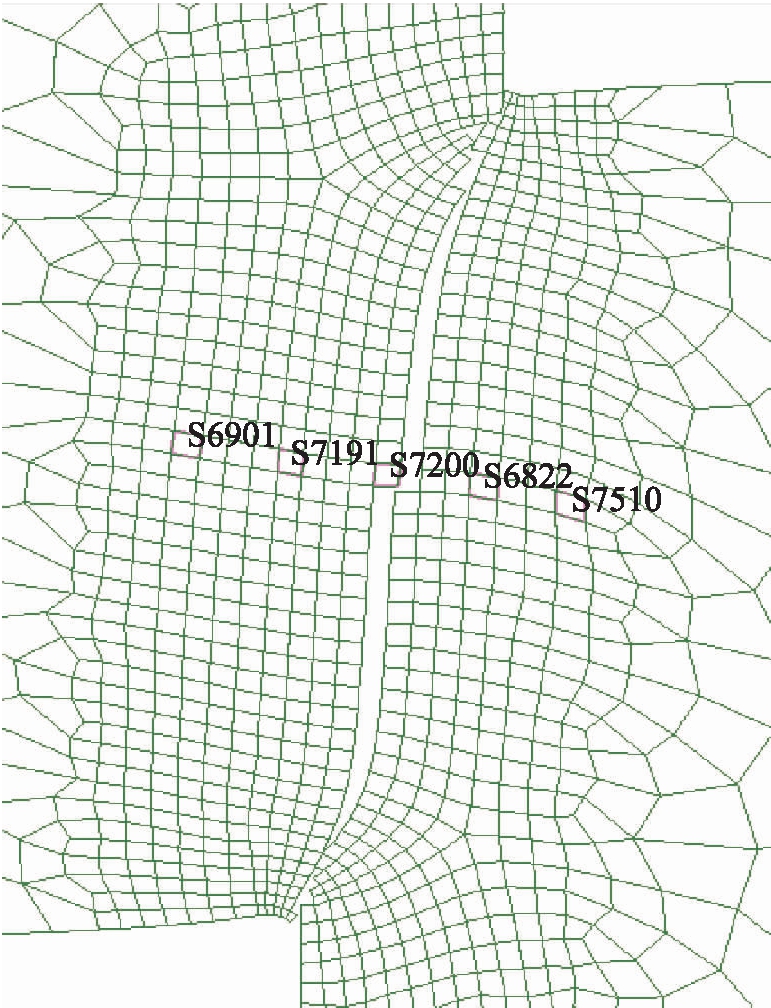
图7 特征单元的编号及位置
Fig.7 Number and location of feature element
绘制AZ31镁合金与6065铝合金特征单元的应力应变时程曲线，结果如图8所示.由图8a可知，AZ31镁合金的应力增长速度关系为VS7200>VS6822>VS7191>VS7510>VS6901，其应力最大值为282.233 MPa.由图8b可知，6065铝合金的应力增长速度关系为VS7200>VS6822>VS7191>VS7510>VS6901，其应力最大值为570.745 MPa.通过对比分析后发现，两种合金的5个特征单元的应力变化过程相似，因此，两种合金局域化变形过程中的应力影响区范围相似，但同等时间内6065铝合金的应力增加效果更加明显，表明6065铝合金的应变硬化和应变率硬化效果更加显著.由图8c可知，在AZ31镁合金的局域化变形过程中，塑性应变 增长速度关系为
≈
≈
，由此可见，在整个变形过程中局域化变形带法向方向上的塑性应变呈对称分布.由图8d可知，在6065铝合金局域化变形过程中，塑性应变增长速度关系为
≫
≈
≈
≈，由此可见，在整个变形过程中局域化变形带都是极为狭窄的.此外，两种合金中编号为S7200的特征单元中均产生了明显的应力塌陷现象，且6065铝合金的应力塌陷产生时间约为10 ms，而AZ31B镁合金的应力塌陷产生时间约为35 ms，表明在变形过程中AZ31镁合金的应变和应变率硬化作用效果低于6065铝合金.
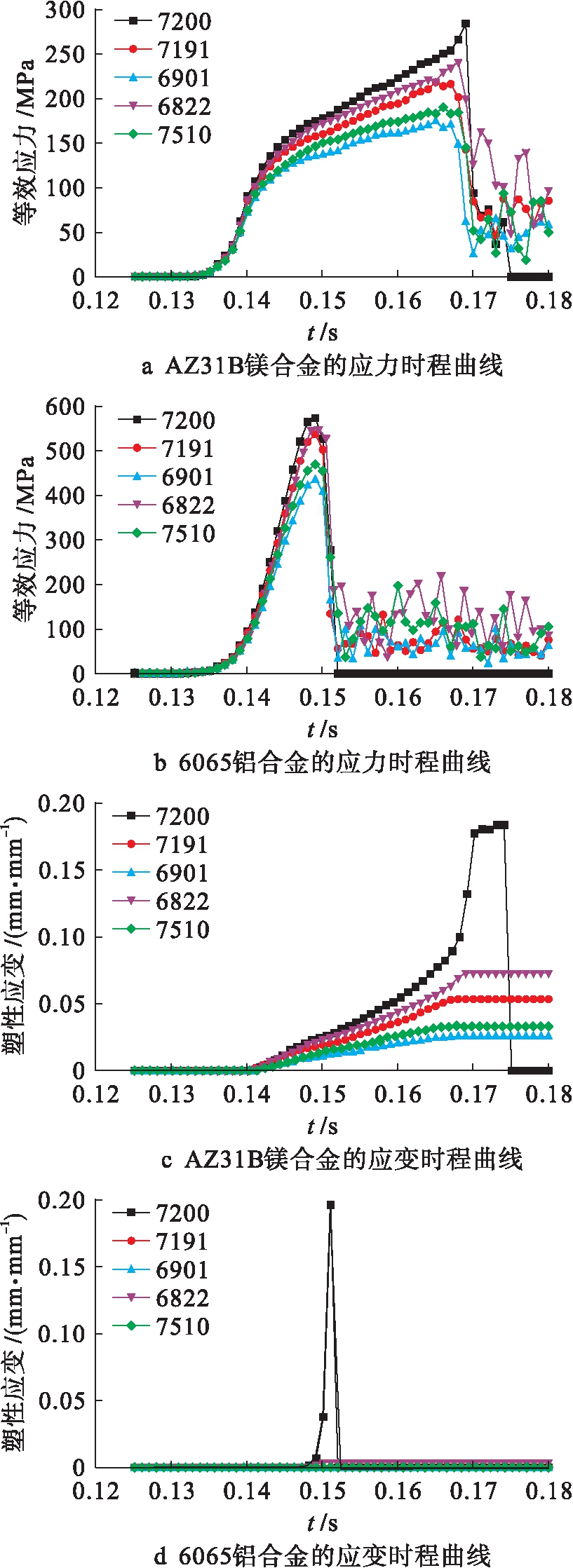
图8 两种合金的应力与应变时程曲线
Fig.8 Time history curves for stressand strain of two alloys
3 结 论
利用ANSYS/LSDYNA数值模拟软件、Johnson-Cook本构方程及其累积损伤本构方程，通过数值模拟分析再现了高应变速率条件下AZ31B镁合金和6065铝合金帽状试样的动态变形过程，得到了如下结论：
1) 在AZ31B镁合金和6065铝合金的变形过程中，两者的裂纹萌生和扩展过程相似，但6065铝合金的塑性影响区更加狭窄且塑性应变累积损伤临界值较高.
2) 在室温条件下当子弹冲击速度为13 m/s时，AZ31镁合金的模拟温升最大值为588.3 K，不易于绝热剪切带的形成.6065铝合金的模拟温升能够达到671 K，易于形成绝热剪切带.
3) AZ31B镁合金和6065铝合金的塑性应变值在局域化变形带由内向外均呈对称分布，变形过程中均产生了应力塌陷现象，但6065铝合金的应变和应变率硬化范围小于AZ31B镁合金，而其强化效果高于AZ31B镁合金.
参考文献(References)：
[1] Feng F，Huang S，Meng Z，et al.A constitutive and fracture model for AZ31B magnesium alloy in the tensile state [J].Materials Science & Engineering A，2014，594(4)：334-343.
[2] Tang L，Chen Z Y，Zhan C，et al.Microstructural evolution in adiabatic shear bands of copper at high strain rates：electron backscatter diffraction characterization [J].Materials Characterization，2012，64：21-26.
[3] Zheng C，Wang F，Cheng X，et al.Capturing of the propagating processes of adiabatic shear band in Ti-6Al-4V alloys under dynamic compression [J].Materials Science & Engineering A，2016，658：60-67.
[4] Choung J，Nam W，Lee J Y.Dynamic hardening behaviors of various marine structural steels considering dependencies on strain rate and temperature [J].Marine Structures，2013，32(3)：49-67.
[5] 毛萍莉，刘超，刘正.不同温度下AZ31镁合金绝热剪切变形局域化 [J].沈阳工业大学学报，2014，36(4)：379-383.
(MAO Ping-li，LIU Chao，LIU Zheng.Adiabatic shear deformation localization of AZ31 magnesium alloy at different temperatures [J].Journal of Shenyang University of Technology，2014，36(4)：379-383.)
[6] 刘正，董阳，毛萍莉，等.轧制AZ31镁合金板材(4 mm) 动态压缩性能与失效行为 [J].材料工程，2015，43(2)：61-66.
(LIU Zheng，DONG Yang，MAO Ping-li，et al.Dynamic compressive properties and failure behavior of rolled AZ31 magnesium alloy sheet (4 mm) [J].Journal of Materials Engineering，2015，43(2)：61-66.)
[7] Yang Y，Jiang L.Self-organization of adiabatic shear bands in ZK60 magnesium alloy [J].Materials Science & Engineering A，2016，655：321-330.
[8] 毛萍莉，刘遵鑫，刘正，等.晶粒大小对AZ31镁合金绝热剪切敏感性的影响 [J].沈阳工业大学学报，2015，37(5)：494-499.
(MAO Ping-li，LIU Zun-xin，LIU Zheng，et al.Effect of grain size on adiabatic shear sensitivity of AZ31 magnesium alloy [J].Journal of Shenyang University of Technology，2015，37(5)：494-499.)
[9] Liu Z，Dong Y，Mao P L，et al.Dynamic tensile and compressive properties of vacuum and ordinary die-casting AT72 magnesium alloy at high strain rates [J].Journal of Magnesium & Alloys，2013，1(2)：150-162.
[10]Wang X，Shi J.Validation of Johnson-Cook plasticity and damage model using impact experiment [J].International Journal of Impact Engineering，2013，60(10)：67-75.
[11]He A，Xie G，Zhang H，et al.A modified Zerilli-Armstrong constitutive model to predict hot deformation behavior of 20CrMo alloy steel [J].Materials & Design，2014，56(4)：122-127.
[12]Hernandez C，Maranon A，Ashcroft I A，et al.A computational determination of the Cowper-Symonds parameters from a single Taylor test [J].Applied Mathematical Modelling，2013，37(7)：4698-4708.
[13]魏志刚，李永池，李剑荣，等.冲击载荷作用下钨合金材料绝热剪切带形成机理 [J].金属学报，2000，36(12)：1263-1268.
(WEI Zhi-gang，LI Yong-chi，LI Jian-rong，et al.Formation mechanism of adiabatic shear band in tungsten heavy alloys [J].Acta Metallurgica Sinica，2000，36(12)：1263-1268.)
[14]李建崇，李树奎，范群波.TC4合金绝热剪切动态演变过程数值模拟研究 [J].稀有金属材料与工程，2010，39(12)：2193-2195.
(LI Jian-chong，LI shu-kui，FAN Qun-bo.The simulation research of TC4 alloy adiabatic shear dynamic evolution process [J].Rare Metal Materials and Engineering，2010，39(12)：2193-2195.)
[15]Rittel D，Wang Z G.Thermo-mechanical aspects of adiabatic shear failure of AM50 and Ti6Al4V alloys [J].Mechanics of Materials，2008，40(8)：629-635.
[16]Wang B，Ma R，Zhou J，et al.Adiabatic shear localization in ultrafine grained 6061 aluminum alloy [J].Materials Science & Engineering A，2016，675：221-227.