合金是一种化合物,并于20世纪得到广泛应用.生活中最常用的合金包括不锈钢、铝合金、铁合金与铜锌合金等,在合金的冶炼过程中如果改变添加元素的含量,则会改变合金的某些物理性质和化学性质.例如,将适量Sn添加到青铜中,可以提高青铜的塑性和抗腐蚀性;将适量Mn和Mg添加到铝合金中,可以提高铝合金的塑性和抗腐蚀性;将适量Sn添加到黄铜中,可以提高黄铜的抗海水腐蚀能力;将适量Pb添加到黄铜中,可以提高黄铜的润化性[1-7].钒和稀土是影响铝合金性能的两种原料,且对合金的抗拉强度、伸长率与热裂倾向值均具有一定影响.为了在提高合金产品质量的同时,又能最大化地节省原材料,在生产过程中需要对合金产品性能进行系统研究.
1 实验假设条件
本文主要从在冶炼过程中钒和稀土的添加量 角度出发,对合金产品的抗拉强度、伸长率和热裂倾向值三个指标进行了研究.为了方便分析,在整个研究过程中假定Al-4.5Zn-1.0Mg-0.8Cu合 金中,不含其他影响实验结果的杂质;假设实验过程不受其他外界因素(如湿度、温度和压强等)的影响,即假设实验是在一个环境适宜且相对稳定的条件下进行的.实验获得的具体数据如表1所示.
表1 钒和稀土的添加对合金力学性能和抗热裂性能的影响
Tab.1 Effect of addition of vanadium and rare earth on mechanical properties and thermal cracking resistance of alloy
2 不同添加方案对合金性能的影响
2.1 单独添加钒对合金性能的影响
为了研究钒的添加量与合金抗拉强度、伸长率和热裂倾向值之间的关系,本文采用多项式拟合法,建立以钒的含量为自变量,合金的抗拉强度、伸长率与热裂倾向值分别为三个因变量的拟合函数关系,再分别计算近似函数和实际数据的误差,从而判断拟合函数的拟合效果.
假设给定已知数据点的坐标为(xi,yi)(i=1,2,…,n),则其多项式拟合函数![]() ,其中,ak为多项式系数.已知数据点的误差平方和δ
,其中,ak为多项式系数.已知数据点的误差平方和δ![]() ,其中,yi为函数实际值,且误差平方和越小越好.上述方法称为多项式拟合法,且拟合效果的评价可以通过以下几个方面[8]进行描述:
,其中,yi为函数实际值,且误差平方和越小越好.上述方法称为多项式拟合法,且拟合效果的评价可以通过以下几个方面[8]进行描述:
1) 误差平方和值δ越接近0,拟合效果越好;
2) 相关指数R的取值范围为[0,1],且R2值越接近1,拟合效果越好;
3) 标准差![]() 越接近0,拟合效果越好.
越接近0,拟合效果越好.
在多项式拟合的具体操作中,本文采用MATLAB软件中的函数拟合工具箱CFTOOL进行最小二乘拟合处理,即先将数据导入软件,采用相应向量保存数据,再利用拟合工具箱对数据进行多项式拟合.同时逐次增加多项式次数,观测函数图像并对照实验数据,最终得出拟合效果最佳、误差最小的多项式次数.
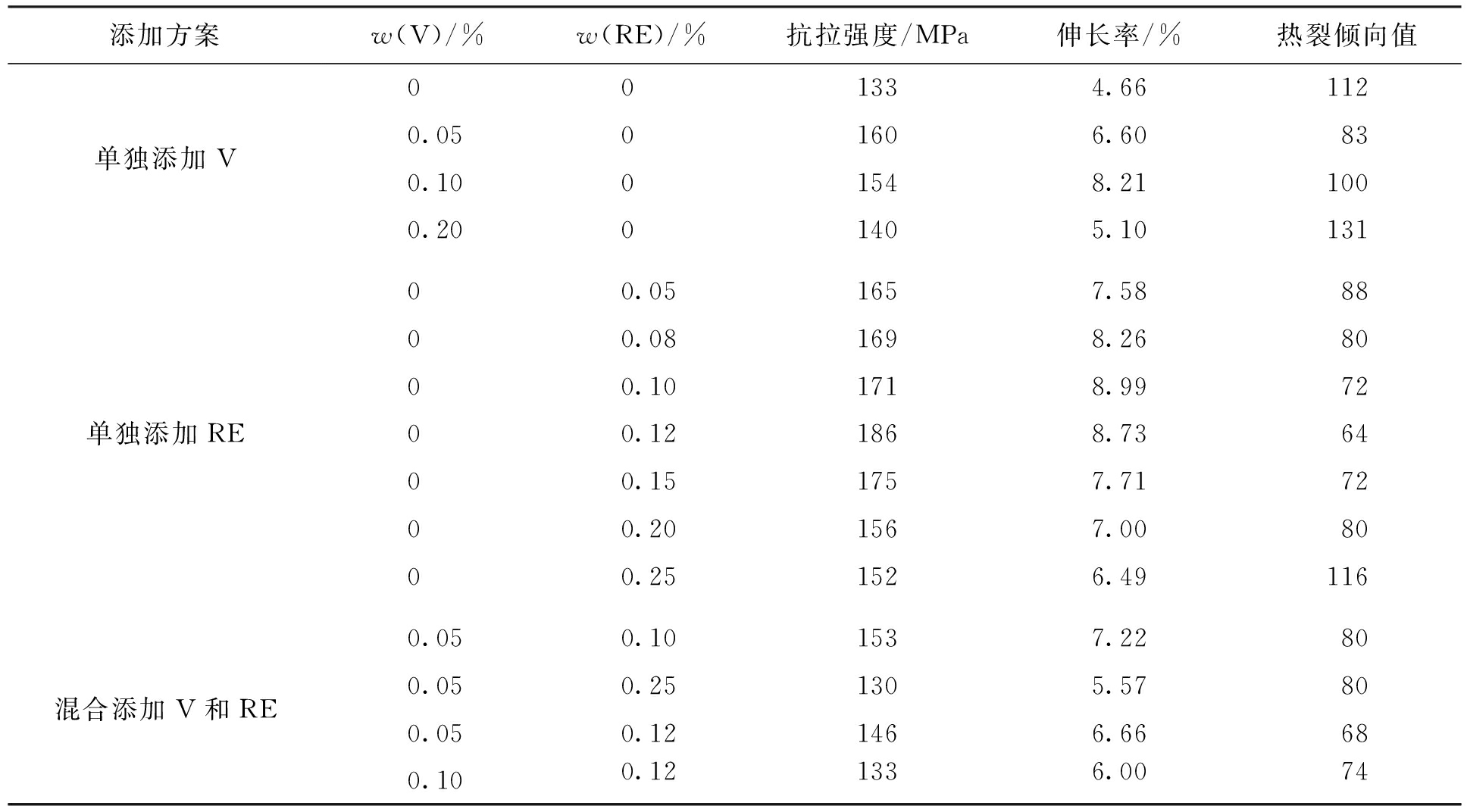
假设钒的添加量为自变量x1,此时合金产品的抗拉强度、伸长率和热裂倾向值分别为因变量f1(x1)、f2(x1)和f3(x1).利用上述多项式拟合模型,结合表1中单独添加钒方案时的实验数据,求出对应的拟合函数图像及拟合函数表达式,具体拟合函数图像如图1所示.通过图1可以得到合金获得最大抗拉强度、最大伸长率和最小热裂倾向值时对应的钒含量.
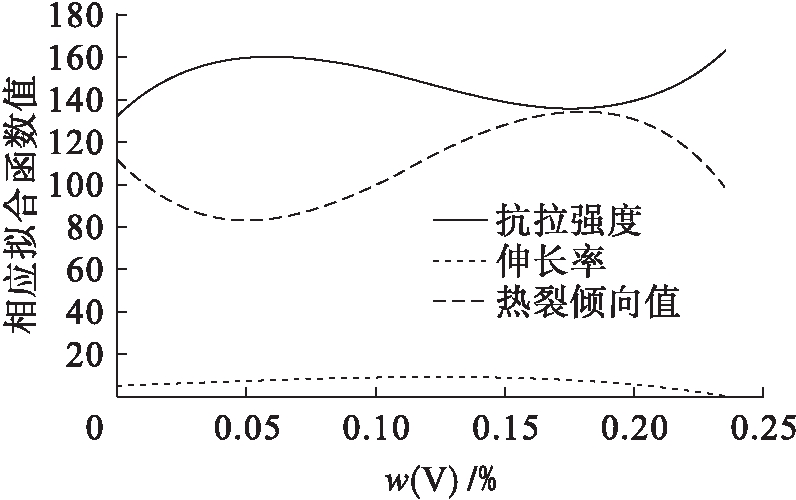
图1 单独添加钒时合金抗拉强度、伸长率和热裂倾向值的拟合函数
Fig.1 Fitting functions of ultimate tensile strength,elongation and hot cracking tendency value of alloy with adding vanadium alone
通过分析可知,单独添加钒时合金抗拉强度的近似拟合函数为
(1)
计算得到其误差平方和为1.858×10-26,相关指数R为1,可见拟合精度较高.
同理可得,单独添加钒时合金伸长率的近似拟合函数为
![]() .2x1+4.66
.2x1+4.66
(2)
计算得到其误差平方和为9.545×10-29,相关指数R为1,可见函数拟合精度也较高.
此外,单独添加钒时合金热裂倾向值的近似拟合函数为
(3)
计算得到其误差平方和为4.786×10-26,相关指数R为1,拟合程度同样较高.
2.2 单独添加稀土对合金性能的影响
沿用上述方法,首先分别求出合金产品的抗拉强度、伸长率和热裂倾向值与稀土添加量之间的三个近似拟合函数,对拟合函数求导并求取极值,之后与函数端点值进行比较后确定最值,从而得到合金性能最佳时所需单独添加稀土的含量.为了对合金的三个指标整体产生较好影响,需要对三个指标函数进行整体分析.为了便于观察,本文对函数进行了相应处理,再综合给定的约束条件,观察三个函数图像的走向趋势,并运用相关软件最终确定自变量的取值,即单独添加稀土的含量.
利用表1中单独添加稀土方案的数据,假设稀土含量x2∈[0,0.25],合金产品的抗拉强度、伸长率和热裂倾向值分别为f1(x2)、f2(x2)和f3(x2),可得合金的三个指标关于稀土含量的拟合函数图像如图2所示.
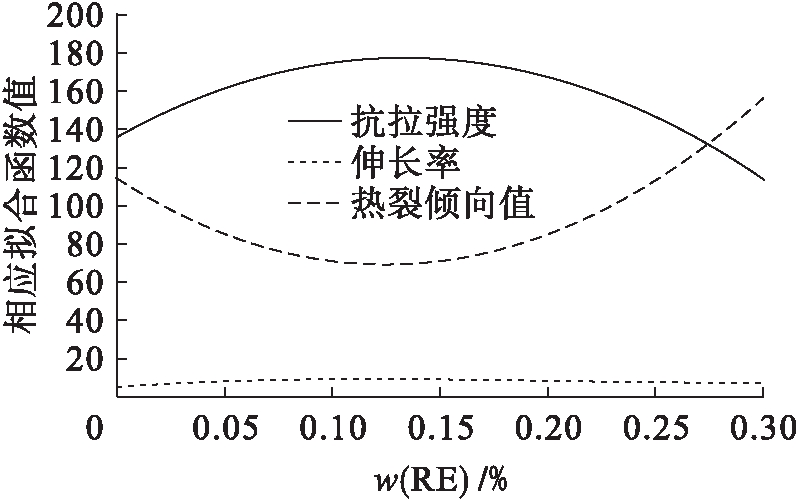
图2 单独添加稀土时合金抗拉强度、伸长率和热裂倾向值的拟合函数
Fig.2 Fitting functions of ultimate tensile strength,elongation and hot cracking tendency value of alloy with adding rare earth element alone
分析图2可知,单独添加稀土时合金三个指标关于稀土含量的函数关系分别为
![]() .5x2+136
.5x2+136
(4)
![]() .
.![]() .44x2+4.59
.44x2+4.59
(5)
![]() .8
.8
(6)
根据上述函数表达式可以分别求出合金抗拉强度、伸长率和热裂倾向值的极值及其对应的稀土含量.将单独添加稀土时合金抗拉强度拟合函数的极大值176.859 MPa与已知数据中合金抗拉强度的端点值133、152 MPa进行比较,可得合金抗拉强度最大值为176.859 MPa,对应稀土质量分数为0.134 1%,即当单独添加质量分数为0.134 1%的稀土时,合金的抗拉强度最大.将单独添加稀土时合金伸长率拟合函数的两个极值8.598%和6.45%与已知数据中合金伸长率的端点值4.66%和6.49%进行比较,可得合金伸长率最大值为8.598%,对应稀土的质量分数为0.098 9%,即单独添加稀土的质量分数为0.098 9%时,合金的伸长率最大.将热裂倾向值拟合函数的极小值68.999与已知数据中合金热裂倾向值的端点值112和116进行比较,可得合金热裂倾向值的最小值为68.999,此时对应的稀土质量分数为0.126 2%,即单独添加稀土的质量分数为0.126 2%时,合金的热裂倾向值最小.
为了求出使得合金的抗拉强度和伸长率较大,但热裂倾向度较小时,需要单独添加的稀土含量,将图2整合为便于观察合金三个指标关于稀土含量的整体变化趋势图.在具体操作过程中,将合金抗拉强度与稀土含量的对应数值缩小20倍,合金热裂倾向值与稀土含量的对应数值缩小10倍,并保持合金伸长率与稀土含量的对应数值不变,从而在同一坐标系内作出三个函数图像并方便观察其变化趋势,具体结果如图3所示.
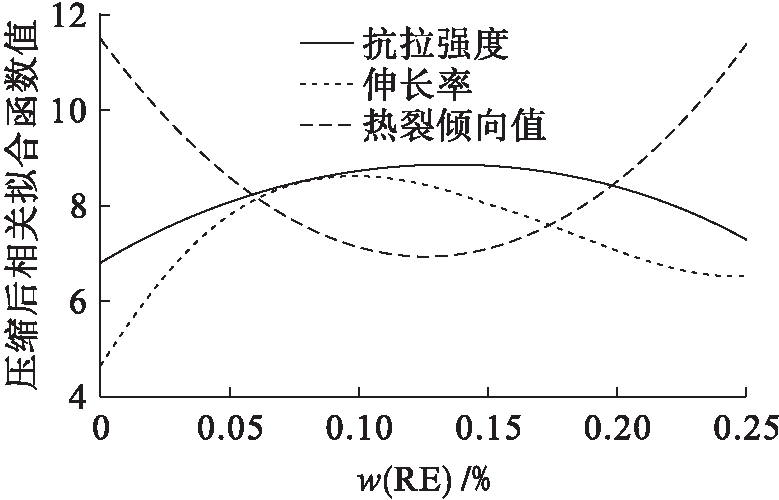
图3 压缩后各指标的整体变化趋势
Fig.3 Overall change trends of differentindexes after compression
为了使得合金的抗拉强度、伸长率较大,热裂倾向值较小,需要构造令合金的抗拉强度、伸长率和热裂倾向值整体效果较好的目标函数z,且z=f1(x2)+f2(x2)-f3(x2).当z取最大值时整体效果最好,且此时x2的取值即为所求稀土含量.利用MATLAB软件计算可得,当x2=0.128%时,合金的整体效果最好,这与图3结果一致,即当单独添加稀土的质量分数为0.128%时,可以提高合金的抗拉强度和伸长率,同时减少合金热裂倾向值,从而使得合金性能的整体效果较好.
2.3 混合添加钒和稀土对合金性能的影响
为了方便起见,采用非线性规划优化模型[8]对合金性能进行系统描述.通常在合金的抗拉强度不低于150 MPa,伸长率不低于7%,同时热裂倾向值尽可能小的情况下,合金使用率最为广泛.首先利用拟合法分别求出合金抗拉强度、伸长率和热裂倾向值关于自变量钒和稀土添加量的函数关系式,再将抗拉强度不低于150 MPa,伸长率不低于7%视为约束条件,将热裂倾向值减少到最小视为目标函数,根据两个约束条件与表1中钒和稀土的含量范围,可以得出两个自变量的可行解区域,最后在该区域内找出使目标函数值最小的点,此点即为最优解点,且最优解点的横纵坐标分别对应钒和稀土的含量.
在具体求解过程中,根据表1中混合添加钒和稀土方案的实验数据,运用MATLAB软件求得合金的抗拉强度、伸长率和热裂倾向值关于钒含量x1和稀土含量x2的拟合函数图像,具体结果如图4所示.
由图4可得合金三个指标的二元拟合函数表达式为
f1(x1,x2)= 4 484.![]() .
.![]() .419 3x1-
.419 3x1-
79.294 4x2+197.948 6
(7)
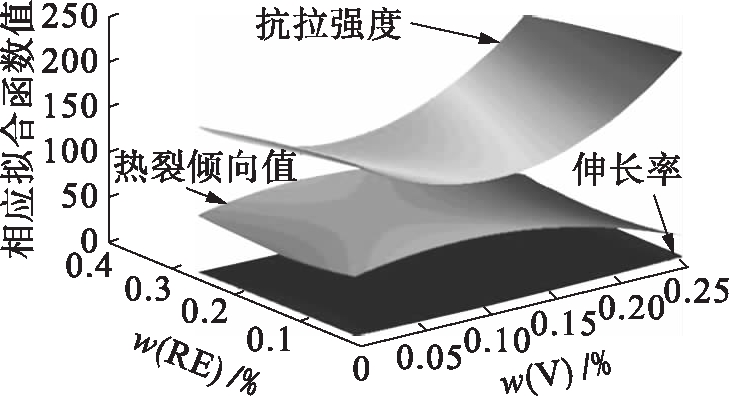
图4 混合添加钒和稀土时合金抗拉强度、伸长率和热裂倾向值的拟合函数
Fig.4 Fitting functions of ultimate tensile strength,elongation and hot cracking tendency value of alloy with mixed addition of vanadium and rare earth
f2(x1,x2)= 183.![]() .
.![]() .600 1x1+
.600 1x1+
8.471 9x2+8.448 2
(8)
f3(x1,x2)= -1 829.![]() .
.![]()
282.999x1-145.798 6x2+74.004 8
(9)
依据非线性优化模型原理可得目标函数与约束条件分别为
min f3(x1,x2)= -1 829.![]() .
.![]()
282.999x1-145.798 6x2+
74.004 8
(10)
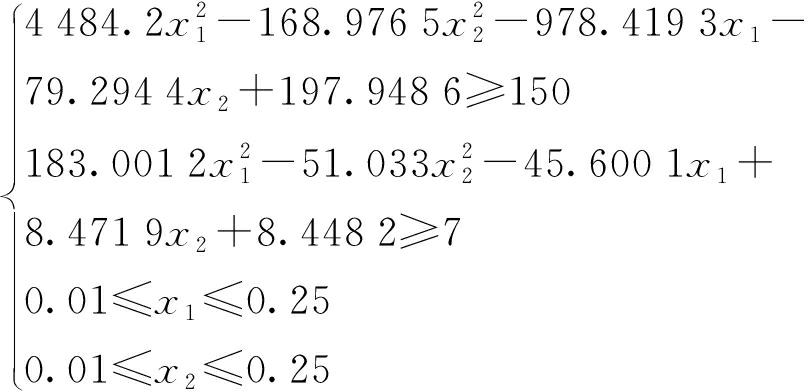
(11)
利用MATLAB软件进行处理后可知,当且仅当x1=0.01%、x2=0.14%时,合金的热裂倾向值最小,且最小值为66.618 9,即当混合添加质量分数分别为0.01%的钒和0.14%的稀土时,才能在合金的抗拉强度不低于150 MPa,伸长率不低于7%的情况下,使得合金的热裂倾向值最小.
3 最优方案模型的建立与求解
3.1 模型建立
本文采用主成分分析法对多种方案进行评价,主成分分析法的基本原理[9-11]为:
1) 在n维实向量空间Rn中,全体单位向量的集合记为E={LLTL=1,L∈Rn}.设X=(X1,X2,…,Xn)T为n维随机向量,L1,L2,…,Ln为Rn中n个不同的单位向量,即Li∈E.构造新变量Z1,Z2,…,Zn,且![]() (j=1,2,…,n).由主成分定义可知,求取随机向量X的主成分Z1,Z2,…,Zn的关键是要求出系数向量M1,M2,…,Mn.
(j=1,2,…,n).由主成分定义可知,求取随机向量X的主成分Z1,Z2,…,Zn的关键是要求出系数向量M1,M2,…,Mn.
2) 列出原始数据矩阵,并计算每个指标的均值![]() 和方差
和方差![]() .Xti(i=1,2,…,p)表示原指标体系中的某个随机变量,其标准化形式为
.Xti(i=1,2,…,p)表示原指标体系中的某个随机变量,其标准化形式为
(12)
(13)
3) 将原始数据矩阵标准化后,得出标准化后的数据矩阵.令![]() 表示原始指标数据标准化后的元素,得到由原有随机向量样本生成标准化后的样本矩阵Y=(ytj)N×p.
表示原始指标数据标准化后的元素,得到由原有随机向量样本生成标准化后的样本矩阵Y=(ytj)N×p.
4) 计算各样本相关系数rij,得出样本相关矩阵H,则样本相关系数与相关矩阵表达式分别为
(14)
(15)
5) 求解相关矩阵的特征值λj、相应的正则化特征向量Mj与正则化特征向量矩阵M,此时主成分集Zj=YMj,综合评价值![]() .
.
欲从单独添加钒、单独添加稀土、混合添加钒和稀土这三种添加方案中,选出对提高合金的抗拉强度和伸长率并减少热裂倾向值的整体效果更加明显的方案,可以依据上述主成分分析法评价模型对三个方案进行评价,并根据最终评价值确定最优方案.但在评价之前需要对各方案的指标数据进行预处理.首先选取各指标的平均值作为评价模型的原始数据,其次对原始样本数据矩阵进行标准化处理,继而得到标准矩阵,再求出各样本的相关系数得到样本相关矩阵,进而求出各指标特征值,并依据特征值的大小确定主成分集和特征向量矩阵,最后依据综合评价值计算公式,得到各方案的综合评价值,从而确定最优方案.
3.2 计算结果
1) 原始数据矩阵表达式为

三个指标的均值分别为![]() .819 4、
.819 4、![]() .788 9和
.788 9和![]() .944 4;三个指标的标准差分别为S1=8.586 8、S2=0.642 5和S3=16.111 9.
.944 4;三个指标的标准差分别为S1=8.586 8、S2=0.642 5和S3=16.111 9.
2) 标准化后样本矩阵为
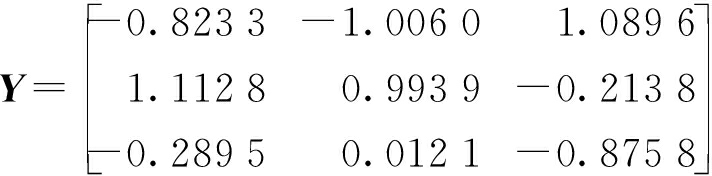
3) 样本相关矩阵为

4) 三个指标的相关矩阵特征值分别为λ1=0、λ2=0.599 3和λ3=2.400 7.正则化特征向量矩阵为

综合评价矩阵表达式为
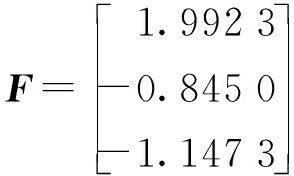
综上所述,综合评价矩阵中单独添加微量钒方案的评价值最大,因而为最优方案.
4 结 论
本文主要从钒和稀土在冶炼过程中的添加量角度出发,针对钒和稀土添加方案对合金产品的抗拉强度、伸长率和热裂倾向值三个指标的影响进行了分析,利用主成分分析法评价模型对三个方案进行评价,由三个方案的最终评价值可以确定最优方案为第一种方案,即单独添加微量钒的方案.同时本文模型均通过了相应的软件检验,具有较强的科学性和可行性,本文方案和结果可以为合金冶炼等相应部门提供应用参考.
参考文献(References):
[1] 黄佰成.稀土微合金化对Al-4Cu-1.5Mg-Mn合金组织与性能的影响 [D].合肥:安徽农业大学,2016.
(HUANG Bai-cheng.Effect of rare earth micro alloying on microstructure and properties of Al-4Cu-1.5Mg-Mn alloy [D].Hefei:Anhui Agricultural University,2016.)
[2] 兰滢.Al-Zn-Mg-Cu-Zr-Sc合金的时效析出行为及力学性能 [D].沈阳:沈阳工业大学,2015.
(LAN Ying.Aging precipitation behavior and mechanical properties of Al-Zn-Mg-Cu-Zr-Sc alloy [D].Shenyang:Shenyang University of Technology,2015.)
[3] 唐玲.热处理对Al-Cu-Mg-La合金的组织及力学性能的影响 [D].沈阳:沈阳工业大学,2014.
(TANG Ling.Effect of heat treatment on microstructure and mechanical properties of Al-Cu-Mg-La alloy [D].Shenyang:Shenyang University of Technology,2014.)
[4] Rownaghi A A,Yun T Y,Rezaei F,et al.Influence of rare-earth and bimetallic promoters on various VPO catalysts for partial oxidation of n-butane [J].Catalysis Letters,2009,130(3/4):504-516.
[5] 代丽.稀土元素Y和Gd对Mg-Al系压铸镁合金组织和性能的影响 [D].沈阳:沈阳工业大学,2014.
(DAI Li.Effect of rare earth elements Y and Gd on microstructure and properties of Mg-Al alloy die-casting magnesium alloys [D].Shenyang:Shenyang University of Technology,2014.)
[6] 余姗姗,朱家明,陈媛,等.钒和稀土对合金性能影响状况的研究 [J].九江学院学报(自然科学版),2015,30(3):17-21.
(YU Shan-shan,ZHU Jia-ming,CHEN Yuan,et al.A study of vanadium and rare earth’s effect on alloy property [J].Journal of Jiujiang University(Natural Sciences),2015,30(3):17-21.)
[7] 曹喆,周立敏,孙文康.钒和稀土对合金性能影响的定量评估 [J].内蒙古煤炭经济,2015(7):187-189.
(CAO Zhe,ZHOU Li-min,SUN Wen-kang.Quantitative evaluation of effect of vanadium and rare earth on properties of alloy [J].Inner Mongolia Coal Economy,2015(7):187-189.)
[8] 李孟莹,张楠,童易成,等.基于多种方法分析钒与稀土对合金性能的影响 [J].湖州师范学院学报,2015,37(8):11-16.
(LI Meng-ying,ZHANG Nan,TONG Yi-cheng,et al.Effect of vanadium and rare earth on the properties of alloys based on a variety of methods [J].Journal of Huzhou University,2015,37(8):11-16.)
[9] 唐冲.基于MATLAB的非线性规划问题的求解 [J].计算机与数字工程,2013,41(7):1100-1102.
(TANG Chong.Solution of nonlinear programming problem based on MATLAB [J].Computer & Digital Engineering,2013,41(7):1100-1102.)
[10]殷焕武,张俊光.基于主成分法的投资项目多方案评价 [J].工业工程,2008,11(5):128-130.
(YIN Huan-wu,ZHANG Jun-guang.Evaluation of multi-projects based on main-element analysis [J].Industrial Engineering Journal,2008,11(5):128-130.)
[11]李克宇.基于主成分分析法的土地整治项目优先度评价研究 [D].兰州:甘肃农业大学,2012.
(LI Ke-yu.The research on the priority evaluation of land consolidation and rehabilitation projects based on principal component analysis [D].Lanzhou:Gansu Agricultural University,2012.)