随着机器人技术的快速进步，机器人已经被广泛地应用在工业、军事、服务业以及危险环境等领域[1].移动机器人的环境探索任务可以看作是根据特定的性能指标或效用函数，使机器人无重复地并以较优化的路径来遍历工作环境中的所有探索点，从而提高机器人环境探索的效率.该任务在安保机器人巡逻、军用机器人扫雷以及工业的运输搬运机器人等领域有广泛的应用，因此，所涉及的任务分配和路径规划等问题成为目前移动机器人研究的重点和热门领域[2].
机器人环境探索就是机器人使用路径规划方法找出一条最优路径[3]，近年来出现一些智能方法，如蚁群算法[4]、改进遗传算法[5-6]以及神经网络方法[7]等.遗传算法是一种新型的、广泛应用于环境探索系统中的路径规划方法[8]，目的是对机器人的探索环境进行规划，通过最后的环境探索路径确定任务点的探索顺序.对于复杂的探索任务，由于过多的环境探索点往往导致单个机器人规划效率低下甚至不能获取优化路径，因此难以满足当前需求.相比较单机器人而言，多机器人具备诸多优点，如多机器人数据采集信息及处理结果共享，机器人合作完成复杂的工作等.
基于此，本文研究了多机器人任务分配和路径规划策略的探索方法.任务分配机器人根据与待探索任务点距离进行分配，路径规划使用改进的免疫遗传算法对分配到的待探索任务点进行探索路径优化.
1 多机器人多任务分配
机器人的复杂工作任务往往是由一系列的多个子任务组成，而这些子任务可以由多个机器人共同完成[9]，因此需要良好的策略充分考虑机器人及任务因素将多任务分配给多个机器人，任务分配即将一项工作划分为多项子任务分配给多个机器人以提高工作效率的策略.多机器人环境探索及任务描述如图1所示.
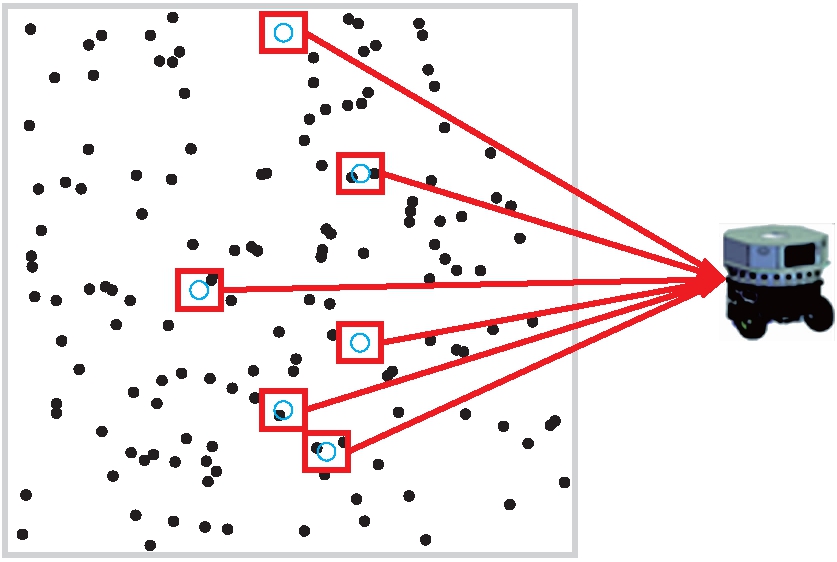
图1 多机器人环境探索任务描述
Fig.1 Description of multi-robot environmentexploration task
图1中，矩形框中圆圈表示机器人，黑色圆点表示探索环境中任务点.由于本文的研究重点在机器人环境探索方面，因此，在环境探索之前的任务分配简单地考虑机器人与任务点之间的距离，将任务分配至距离最近的机器人.
本文中的多机器人任务分配策略主要基于探索任务点与机器人的最邻近原则，即优先为每个机器人分配距离最近的探索任务点.i号机器人初始位置为
，j号任务的位置为pj，i号机器人完成j号任务所需行走距离为dij.其中，i∈[0，N-1]，j∈[0，M-1].本文分配具体步骤如下：
1) 由随机或读取方法产生机器人及任务信息；
2) 计算每个机器人与任务之间的距离dij，计算公式为
(1)
3) 找出距离dij最小的数据，判断j号任务是否被分配，如果是则取下一个次小的距离数据，否则将任务分配给距离最短机器人；
4) 更新i号机器人与j号任务的数据信息，转到步骤3).
2 机器人环境探索
2.1 问题描述及编码
在一系列的任务被分配至机器人后，机器人需要探索这些自身分配到的任务，在探索任务点的过程中需要根据已知的环境信息综合考虑约束条件产生一条最短的最优路径.本文中环境探索是根据免疫遗传算法实现的.机器人路径编码采用的是任务点编号形式，如设有n个任务点，则(1，2，3，…，n)记为一条路径.
2.2 初始路径生成
在对机器人路径规划问题进行抗原呈递后，使用基于任务点编号的路径形式.在免疫遗传算法中需要产生一定数量的初始解，常用的初始解产生方式为随机方法，随机产生初始解的优点是任何路径解出现的概率都相同，在任务点数目较小的情况下产生的路径解极有可能包括最优解，但是当任务点数目较多时路径解的数量以组合的方式快速增长，产生的初始最优解并不是很优.因此，本文在产生初始解时，采用最邻近算法找出一条与全局最优解相近的解，能够明显加快免疫遗传算法的收敛速度.设初始子路径为son，该路径只包含一个任务点，未插入的任务点包含在集合W中，最邻近算法具体步骤为：
1) 从W中取出与son距离最小的点r，将r插入子路径son中，并从W中移除任务点r；
2) 继续从集合W中取出一任务点r，新任务点r为与son中任务点距离最短的任务点，将任务点插入到son中；
3) 重复进行步骤2)操作，直到W中无任务点.
2.3 适应度确定
适应度是免疫遗传算法中评判一条路径好坏的标准[10]，适应度越大说明路径距离越短，反之距离越长，是免疫遗传算法中最重要的计算部分.对于一条路径P(T1，T2，…，Tn)，本文采用的适应度函数f(P)计算公式为
(2)
，Vk+1)+d(Vn，V0)
(3)
式中：d(Vk，Vk+1)为任务点Vk与Vk+1之间的距离；d(P)为整条环形路径的距离；d(best)为当前最优路径距离；f(P)为路径P的适应度，取6次方是为了扩大适应度的间隙.
2.4 算法参数定义
为了保证算法中抗体群的多样性，应该对高浓度的抗体进行抑制，对适应度高、浓度低的抗体进行促进.本文采用的方法是动态改变抗体的选择概率，使得浓度高、适应度低的抗体选择概率较小，否则选择概率较大.
2.4.1 抗体浓度
在抗体种群大小为m的种群中，第l个抗体的浓度为
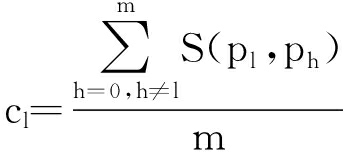
(4)
式中，S(pl，
，ε为一个较小的实数，g(pl，ph)=similar(pl，ph)-1，similar(pl，ph)为路径pl和ph的相似度.
2.4.2 选择概率
在抗体种群大小为m的种群中，第l个抗体的选择概率为PSl，为了对浓度高的抗体进行抑制，对适应度高的抗体进行促进，选择概率计算公式为
(5)
λcl
(6)
式中：
为l号抗体初始最大选择概率；
为l号抗体初始最小选择概率；fl为l号抗体的适应度；cl为l号抗体的浓度；λ为浓度对选择概率的影响决定因子，当λ为0时，本文算法和基本遗传算法相似.
2.4.3 变异概率
在免疫遗传算法中，为了保持高适应度的抗体不被破坏，适应度高的抗体其变异概率应较小，变异算子作用是保证抗体的多样性，因此，本文变异概率设计的目的是当抗体适应度越大时，其变异概率越小；抗体的浓度越大，其变异概率越大.但为了最后群体可以稳定收敛，抗体变异概率应逐渐减小，其变异概率表达式为
·PMmax·
(7)
(8)
式中：fmax为抗体种群中最大适应度；PMmax为抗体初始最大变异概率；PMmin为抗体初始最小变异概率；T为最大迭代次数；t为当前迭代次数.
2.4.4 交叉概率
在抗体种群中，为了使得免疫遗传算法在解搜索范围内不存在某个方向的偏向，而是各个解的搜索方向都应该具有同等的机会，因此抗体之间的交叉概率应相同，但是为了保证算法的稳定性，交叉概率应逐步减小.交叉概率的表达式为
PC=PCmax·
(9)
PC=PCmin (PC<PCmin)
(10)
式中：PCmax为抗体初始最大交叉概率；PCmin为抗体初始最小交叉概率.
3 实验结果及分析
对于多机器人环境探索任务，本文在仿真环境中对其进行实验，实验中机器人数量、机器人位置、任务数量和任务位置等信息都可随机产生也可读取数据文件，图2为本文随机产生的6个机器人及200个任务点的面板示意图，当前显示的是未分配情况图.图2中，数字为机器人的编号，小圆圈为随机生成的任务点.
3.1 多机器人任务分配实验
根据任务分配方法进行多机器人任务分配，本文综合考虑距离的多任务分配，其结果如图3所示.图3中，带有数字的大圆点为机器人，形状各异的点为分配至不同机器人的任务，可以看出每个机器人分配到的任务都集中在机器人附近.
3.2 多机器人环境探索实验
对上述任务分配结果中1号机器人进行环境探索，图4a为本文使用最邻近算法产生初始抗体种群时最优抗体路径，图4b为只采用随机法产生初始抗体种群时的当前最优路径.
图2 多机器人多任务的环境示意图
Fig.2 Schematic diagram of multi-robotand multi-task environment
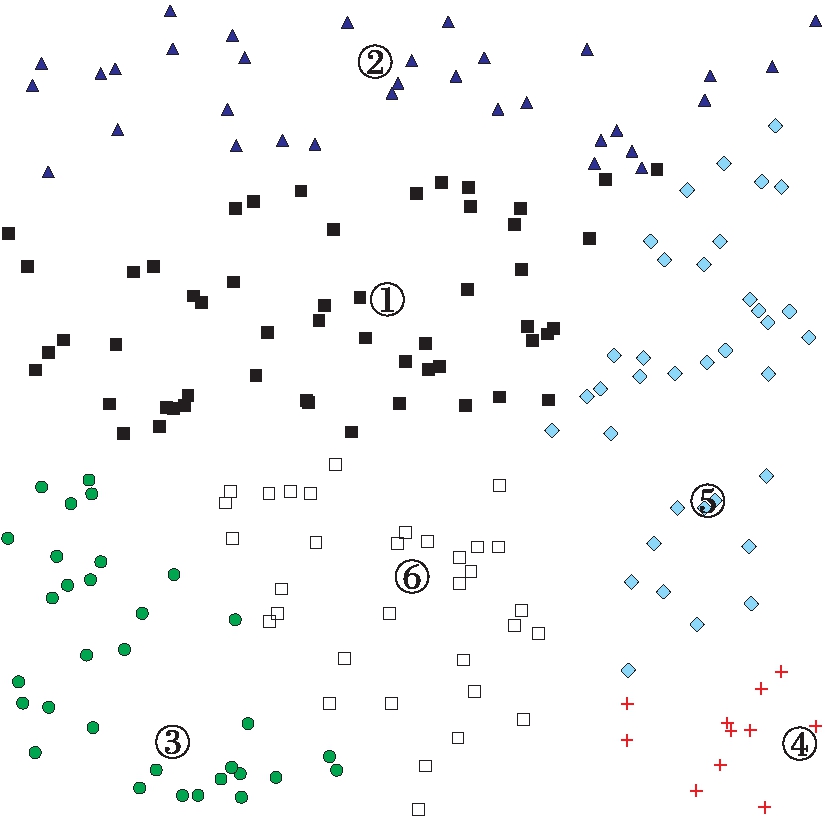
图3 多机器人任务分配示意图
Fig.3 Schematic diagram of multi-robot task allocation
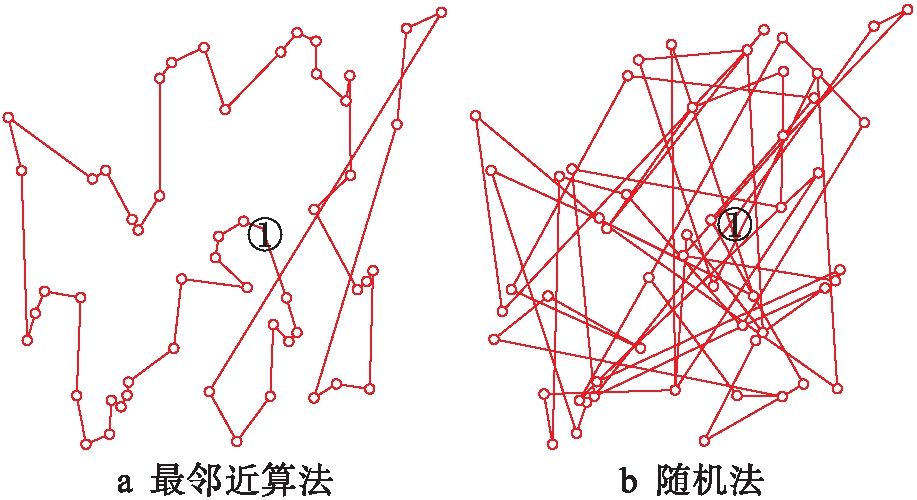
图4 单机器人初始路径图
Fig.4 Initial path diagram of single robot
由图4可以看出，使用最邻近算法产生初始抗体最优解明显比随机法产生初始最优解更接近全局最优解.
为了验证本文提出的改进免疫遗传算法的有效性，分别使用本文算法和遗传算法进行任务点路径规划，并对实验结果进行比较.对于任务分配结果中1号机器人的任务点，图5a为本文算法规划得到的最短路径示意图，图5b为使用遗传算法求得的路径解示意图.
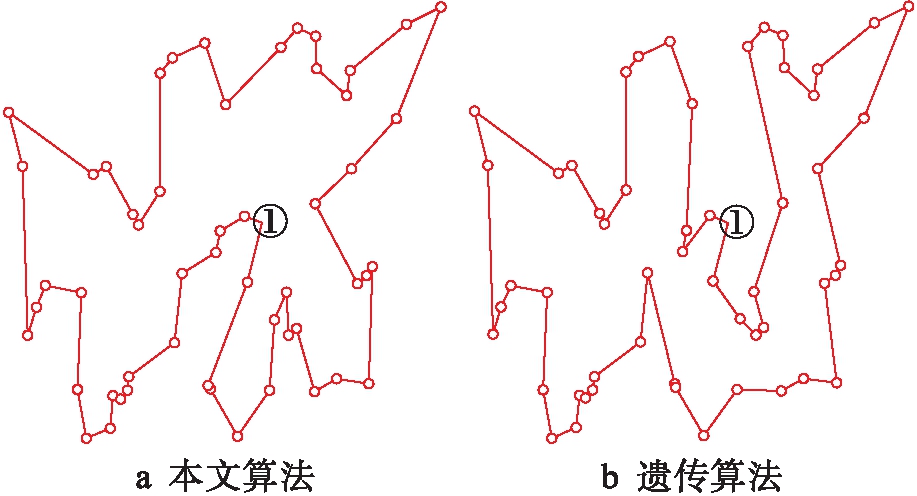
图5 单机器人实验结果对比图
Fig.5 Comparison in experimentalresults of single robot
图6、7分别为本文算法与遗传算法的最佳个体与遗传代数的关系图，可知本文经过294次迭代遗传求解到的最优路径距离为1 826，而遗传算法在迭代1 434次时求解到的距离为1 888.
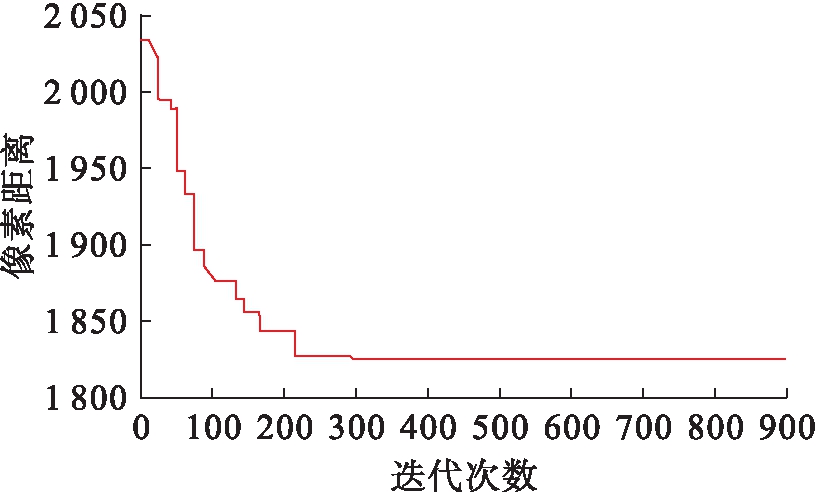
图6 本文算法进化图
Fig.6 Evolution diagram of proposed algorithm
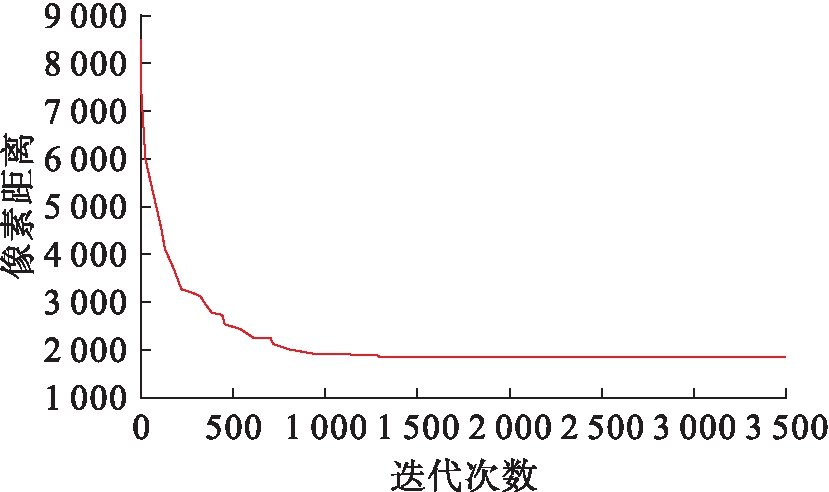
图7 遗传算法进化图
Fig.7 Evolution diagram of genetic algorithm
从图6、7中可以看出，本文方法在开始时的最优路径距离与遗传算法迭代多次的距离相同，且本文方法在迭代约300次完成收敛，而遗传算法在约1 450次完成收敛.结果表明，本文提出的改进免疫遗传算法能够高效地规划出较优路径.
对于图2的任务环境，在进行多机器人任务分配后，分别对1至6号机器人使用本文方法进行环境探索，得到的路径示意图如图8所示.
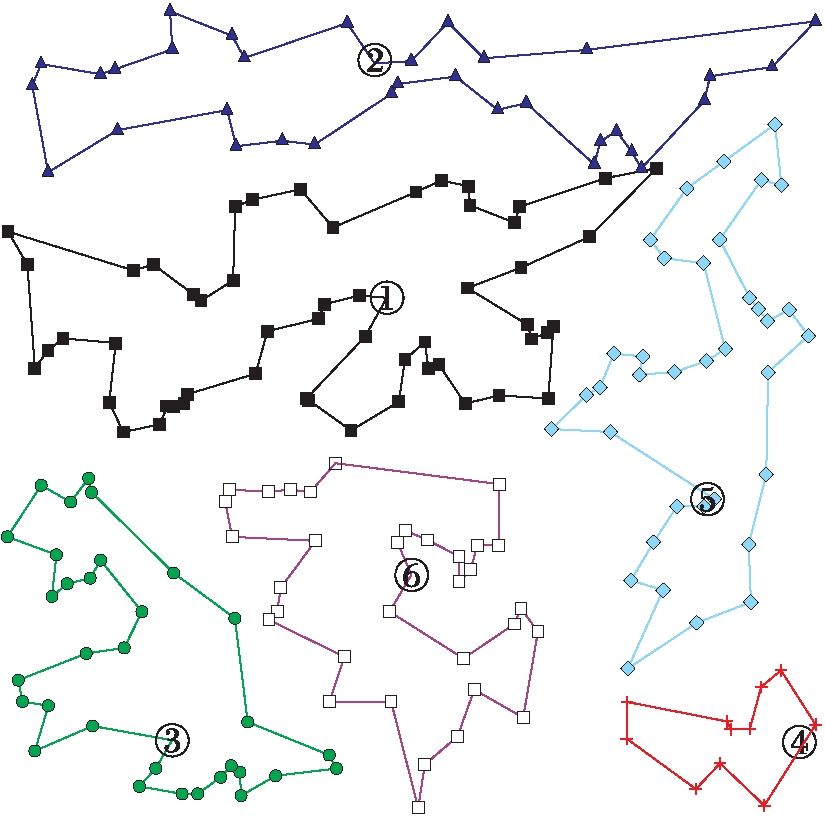
图8 路径规划图
Fig.8 Path planning diagram
为了验证本文方法的有效性和实用性，本实验随机生成另一组多机器人及探索任务点数据，然后进行多机器人探索规划，其结果如图9所示.
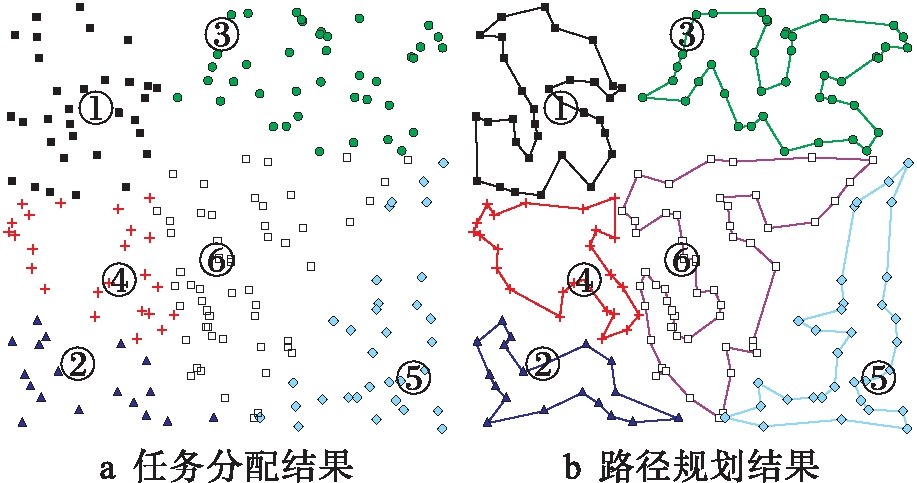
图9 多机器人环境探索实验结果
Fig.9 Experimental results of multi-robotenvironment exploration
4 结 论
本文研究了一种多机器人环境探索方法，首先根据探索任务点的位置分布进行多机器人任务分配，然后利用改进的免疫遗传算法实现路径规划.由实验结果可知，本文算法相对于其他算法在初始抗体种群产生时能够产生较为优化的初始路径，从而提高复杂路径规划效率.此外，对于环境中存在较多探索任务点的情况，通过多机器人协作以降低个体机器人完成任务的复杂度，从而提高全局路径规划效率.
参考文献(References)：
[1] 计时鸣，黄希欢.工业机器人技术的发展与应用综述 [J].机电工程，2015，32(1)：1-13.
(JI Shi-ming，HUANG Xi-huan.Review of development and application of industrial robot technology [J].Mechanical and Electrical Engineering，2015，32(1)：1-13.)
[2] 朱大奇，曹翔.多个水下机器人动态任务分配和路径规划的信度自组织算法 [J].控制理论与应用，2015，32(6)：762-769.
(ZHU Da-qi，CAO Xiang.An improved self-organizing map method for multiple autonomous underwater vehicle teams in dynamic task assignment and path planning [J].Control Theory and Applications，2015，32(6)：762-769.)
[3] Stachniss C，Mozos O N，Burgard W，et al.Efficient exploration of unknown indoor environments using a team of mobile robots [J].Annals of Mathematics and Artificial Intelligence，2008，52(2)：205-227.
[4] 卜新苹，苏虎，邹伟，等.基于复杂环境非均匀建模的蚁群路径规划 [J].机器人，2016，38(3)：276-284.
(BU Xin-ping，SU Hu，ZOU Wei，et al.Ant colony path planning based on non-uniform modeling of complex environment [J].Robot，2016，38(3)：276-284.)
[5] Liu F，Liang S，Xian X.Optimal robot path planning for multiple goals visiting based on tailored genetic algorithm [J].International Journal of Computational Intelligence Systems，2014，7(6)：1109-1122.
[6] 张毅，代恩灿，罗元.基于改进遗传算法的移动机器人路径规划 [J].计算机测量与控制，2016，24(1)：313-316.
(ZHANG Yi，DAI En-can，LUO Yuan.Mobile robot path planning based on improved genetic algorithm [J].Computer Measurement & Control，2016，24(1)：313-316.)
[7] 钱夔，宋爱国，章华涛，等.基于自适应模糊神经网络的机器人路径规划方法[J].东南大学学报(自然科学版)，2012，42(4)：637-642.
(QIAN Kui，SONG Ai-guo，ZHANG Hua-tao，et al.Path planning for mobile robot based on adaptive fuzzy neural network [J].Journal of Southeast University(Natural Science Edition)，2012，42(4)：637-642.)
[8] Juli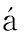
M，Gil A，Reinoso O.A comparison of path planning strategies for autonomous exploration and mapping of unknown environments [J].Autonomous Robots，2012，33(4)：427-444.
[9] 么立双，苏丽颖，李小鹏.多机器人系统任务分配的研究与发展 [J].制造业自动化，2013，35(5)：21-24.
(YAO Li-shuang，SU Li-ying，LI Xiao-peng.Overview of research on multiple mobile robots task allocation [J].Manufacturing Automation，2013，35(5)：21-24.)
[10]陈果，邓堰.遗传算法特征选取中的几种适应度函数构造新方法及其应用 [J].机械科学与技术，2011，30(1)：124-128.
(CHEN Guo，DENG Yan.Several new methods for features extraction based on genetic algorithm and their application [J].Mechanical Science and Technology，2011，30(1)：124-128.)