尽管信息时代已经迈入了千家万户,但互联网业务和流量仍在不断地发展和增长.互联网业务不仅倾向于数量的增加,而且对质量的要求也在明显提高[1-3].此外,新兴技术如物联网、远程监控和云计算也需要大量具有实时性要求的流量和全球网站的互连,因此,除了具有QoS性能的网络外,这些服务还需要一种端到端的QoS来连接各种多样化的载体网络[4-6].如今的电信市场主要集中在流量服务方面,为了满足客户期望,电信公司被迫在容量上进行大量投资,而这些投资如果不能获得足够的回报,就无法维持可持续的经营.在这种情况下,现存的互联网商业规则可能无法为域间互连网络中价值链(主要包括网络应用提供商和网络服务提供商等)的所有参与者提供一个可持续发展的经济效益.事实上,现存的对等协议规则并不知道全部域的QoS性能,而且多数是以流量对称为前提,这使不断发展和高质量要求的服务不能得到满足.此外,对于绝大多数互联网连接来说,最常见的定价方式是月费率(即按月定价付费),而其他的参与者如应用提供商APs或顶层供应商(over the top providers,OTTs)获得的收益是按每消耗的带宽为基础的,这依赖于现有网络基础设施上的服务,从而造成网络提供商不能获得足够的报酬[7].已有许多互联网公司和学术机构在积极研究和分析未来的发展趋势,以期得到满足端到端的需求和各种可操作的商业模式.自治系统(autonomous systems,ASs)联盟或联合体的出现,作为一个新兴架构为其提供服务[8].
已有文献提出采用网络带宽拍卖来解决带宽分配问题.这些研究多数是寻求投标机制本身而忽略带宽的有效分配.文献[9]提出了一种适应于P2P网络分布式特性的带宽拍卖分配机制.该机制通过上载带宽支付方式,迫使自私请求节点选择合适的带宽需求,使得整个P2P网络中的节点良性竞争带宽资源,避免了“公共地悲剧”发生,且带宽分配算法在资源节点和请求节点并行执行.文献[10-13]基于Vickrey-Clark-Groves(VCG)机制提出了在多轮喊价中挑选出第一和第二最高喊价,然后依次淘汰,最终确定出最高喊价的方法.这些竞价机制一方面仅集中在喊价高低,目标是利益最大化,而忽视网络服务质量;另一方面,这些机制多数需要集中式计算,其中有些还假设特定的网络拓扑结构,或假设买方知道网络拓扑结构.文献[14]提出了采用第一价格拍卖.在这种拍卖中,尽管目标也是寻求收益最大化,但其实现的复杂性要远低于第二价格和多轮竞价拍卖机制.
针对以上方法的不足,本文在文献[14]第一价格拍卖机制的基础上,一方面,考虑多域联合情形而不是单域情形,即ASs以一种合作的方式协同工作来出售端到端质量确保的比特管道.比特管道不一定要出售给最终用户,而是出售给中间参与者如代理商或OTTs,中间参与者将通过质量保证路径把比特管道转售给最终用户,不但使得端到端的质量参数得到保证,而且还能使整个联盟的收益最大化.另一方面,在考虑端到端的QoS约束和容量约束条件下,提出了一种基于Shapley值的收益分享激励机制,激励联盟中的ASs出售更多优质的服务,从而增加整个联盟收益和其自身的收益分享.仿真结果表明,本文提出的多域联合情形下的带宽分配算法和基于Shapley值的收益分享激励机制,不但能够实现端到端QoS约束下的带宽优化分配,而且能实现整个多域联盟的总收益最大化,并激励各个AS提供更多优质服务而获得更多收益分享.
1 基于带宽优化分配的收益最大化
考虑几个ASs协同工作,以一个多域质量保证路径来出售容量(比特流),称这种质量保证路径为QoS管道或路径.在这种情况下,每个AS按此方法出售的专用容量是其已部署容量的一部分,也就是说,每个AS有其自身的基础设施,可以决定将它们的多大容量提供给联盟.
对于每个QoS管道来说,如果有一组用户/买家愿意获得管道上的一部分带宽,把该组用户/买家愿意为每个数量的带宽支付的金额总数称为效用函数.本文目标就是在实现端到端QoS约束条件下,使整个联盟的收益最大化.一般而言,这种情况下的端到端QoS约束条件就是端到端的延迟约束(即端到端的最大可容许延迟).为了定量化描述这种情况,把联盟中的每个AS用n来表示,等效容量为cn,全部节点集用N来表示,可用的管道是集合S中的管道,表示为s,对路径s上的延迟约束用Ds来表示.假设联盟内的路由固定且为单路径,把这些路由表示为N×S大小的矩阵R,其中,符号·表示集合的基数,如果管道j*的路由穿过节点i*,则Ri*,j*等于1,否则为0,用r(s)表示管道s的路由.分配给管道s的带宽(即出售给与管道s相关联的买家的流量数量)表示为as,与每个管道s相关联的效用函数表示为Us(as),通常情况下,Us(as)是带宽的一个严格的凹函数.
QoS管道是由入口和出口点以及最大延迟来确定的,这意味着2个QoS管道被视为是不同的,尽管2个管道完全共享相同的物理路径,但具有不同的延迟界限.
在一个路径中由每个节点引入的延迟是全部路径经由节点所携带的带宽的递增凸函数,这个函数可以通过某种方式获得或通过域估计得到,节点的延迟函数可表示为fn(an),![]() .
.
出售给全部路径的流量(即带宽)数量必须满足由联盟预计的收益是最大化的,同时还要满足QoS约束条件,故该问题可表示为带宽分配问题.
问题1:
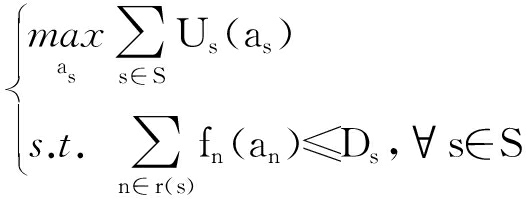
(1)
定理1 原始![]() 对偶算法的收敛性.给定问题1,设
对偶算法的收敛性.给定问题1,设![]() 是严格的凹函数,且fn(an)(∀n∈N)为凸函数,则在式(2)、(3)中定义的迭代
是严格的凹函数,且fn(an)(∀n∈N)为凸函数,则在式(2)、(3)中定义的迭代![]() ∀s∈S)逐渐收敛于问题1的解.
∀s∈S)逐渐收敛于问题1的解.
在问题1中,容量约束条件已经被考虑在fn中,如果fn是一个闸函数(即当带宽接近于容量时,其趋近于无穷大),则可以忽略容量约束.事实上,联盟可能总是出售带宽给某一个路径,如果预计这样做的收益低于某个不被考虑的界限值时,则目标就是采用分布式方法来求解问题1.因此,对问题1采用原始![]() 对偶算法,其相关的拉格朗日表达式为
对偶算法,其相关的拉格朗日表达式为
L(a,λ![]()
(2)
式中,λ={λs}s∈S为拉格朗日乘子向量.
为了找到式(2)的一个鞍点(即问题1的最优解),采用梯度投影算法来更新原始![]() 对偶变量,即
对偶变量,即
(3)
(4)
式中:[·]+=max{0,·};γs和αs为步长大小.
更新式(3)、(4)是在一个管道(也把这个管道称为源)的每个边缘路由器上迭代执行.每个源通过路由r(s)发送一个λs和as的初始值,每个节点接收到全部值并计算延迟和延迟的导数乘上它所接收到的λs的总和,并发送给源,全部这些值用2个和累加并返回到源.因此,在每次迭代中只需要把2个值发送并返回到源,一旦源接收到这些值,就对λs和as的值进行更新.
1.1 多域网络带宽拍卖
将本文算法应用于多域带宽拍卖模型,把每个管道与出售的服务关联起来,这些服务有确定的带宽σs和延迟Ds,通过同一管道的网络带宽拍卖出售.本文采用第一价格拍卖机制,即获胜用户获得投标的数量.
考虑一次性带宽拍卖情形,也就是提供服务的全部可用容量将在某一时刻被拍卖.对于每个服务s来说,有Ns个买家/用户加入到拍卖中来获得一个服务实例.Ns中的每一个买家/用户的出价(投标)为![]() ,其排序为
,其排序为
![]() ≥
≥![]() ≥
≥![]() ≥…≥
≥…≥![]()
(5)
在第一价格拍卖机制下,寻找到使得这些投标可以接受的资源分配判决,以使整个联盟的收益最大化,同时使每个路由的延迟小于给定的延迟约束值.对于每个服务s来说,全部投标都是针对相同的带宽和延迟约束,故最优解就是每个服务可接受的最高出价.定义一个变量ψs,k,如果对服务s的第k个投标被接受,则ψs,k等于1,否则为0;定义一个变量ms为对于服务s可接受的出价数量,可得
(6)
可接受的ms个投标将得到一个总的接受率,即带宽as,且as=σsms.因此,每个服务的效用就可以定义为
(7)
式(7)为as的离散值,本文通过线性插值将其扩展为as的一个分段线性凹函数,则最优化问题可表示为问题2:
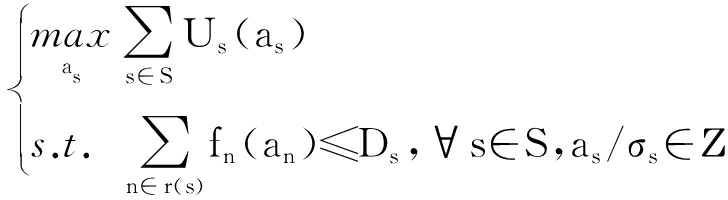
(8)
可知问题2与问题1唯一的差别在于加入了一个整数约束.一方面,本文采用求解问题1最优解的方法和过程来求解实例模型的问题2;另一方面,由于整数规划是NP-hard的,因此,采用凸松弛以及舍入来满足这个整数约束,可以通过在两个连续的整数值之间得到一个跳变结果来使效用函数非严格的凹特性妥协于算法的收敛性.为了避免震荡,还可以采用近点优化法来得到一个严格的凹函数作为目标,而不改变所要得到的解的点.为了出售服务,以周期性的方式重复上述过程,在每个周期时间T内收集全部投标并分配带宽,得到满足整数约束的问题2的最优解即为最大化收益.
1.2 拍卖实例性能仿真
图1为算法应用实例的性能仿真结果.图1a为拓扑结构,本文在网络仿真平台J-Sim环境中进行仿真,J-Sim网络仿真环境可以很容易地建立网络拓扑、节点结构和通讯行为,从而实现网络仿真,达到评价网络算法的目的.拓扑结构中有4个AS联合提供2个服务,对于2个服务来说,有12个买家给出喊价;每个AS的等效容量(带宽)为40,服务1的延迟界限(即延迟约束)D1=2.8,服务2的延迟界限D2=0.25,2个服务提供的带宽数量均为80.图1b为对于每个服务仿真所得到的效用函数.延迟约束小的(D2=0.25,意味着QoS性能更好)服务2获得了更高的喊价,说明在这种端到端QoS约束条件下,本文提出的多域网络带宽拍卖模型在保证更好QoS性能的优化带宽分配下还能获得较高的拍卖价格,说明本文提出的算法是可行和有效的.图1c为仿真得到的2个服务对于算法收敛所需要的迭代过程中带宽as的变化情况.获得更多收益的服务2可以得到更多的可接受带宽.图1d为仿真得到的每个服务所预计的收益变化情况.具有较好端到端QoS约束条件(D2=0.25)下的带宽分配服务2的预期收益要远远高于较差端到端QoS约束条件(D1=2.8)下的带宽分配服务1的预期收益.
2 基于Shapley值激励的收益分享
对于互联网服务来说,传统的对等支付可能并不适合这类有质量保证的服务,因此,基于某种公平原则来实现收益分享变得十分重要.在理想情况下,每个AS的预计收益应当与其提供给联盟的利润成正比,而那些提供端到端QoS性能下降或出现瓶颈的AS,或在某种程度上限制其收益,或鼓励增加提供给联盟的资源.
2.1 Shapley值
Shapley值是由Lloyd Shapley在1952年提出,该方法能够实现一个联合体或联盟的收益分享,因其良好的性能而被广泛应用于各种研究中.
一个具有可转移效用的联盟博弈可表示为(M,v),其中,M是玩家(成员)的一个有限集合,v∈2M→R为与每个联盟Q⊆M相关的价值函数,即成员可以在联盟之间分配到一个有真正价值的报酬v(Q).
给定一个博弈G=(M,v),称x={xi}(∀i∈M)为报酬向量,xi代表玩家i∈M所得到的大联盟M的报酬份额.一个预归集是报酬向量的集合,满足全部xi的总和等于v(M).一个虚拟玩家对联盟的贡献与其想获得的报酬是相同的,采用这些定义,引入对称性(即对任意的v,如果i和j对任意联盟的贡献相同,则xi=xj)、虚拟玩家(即对任意的v,如果i是一个虚拟玩家,则xi=v({i}))和可加性的概念,则Shapley值的定义如下所示.
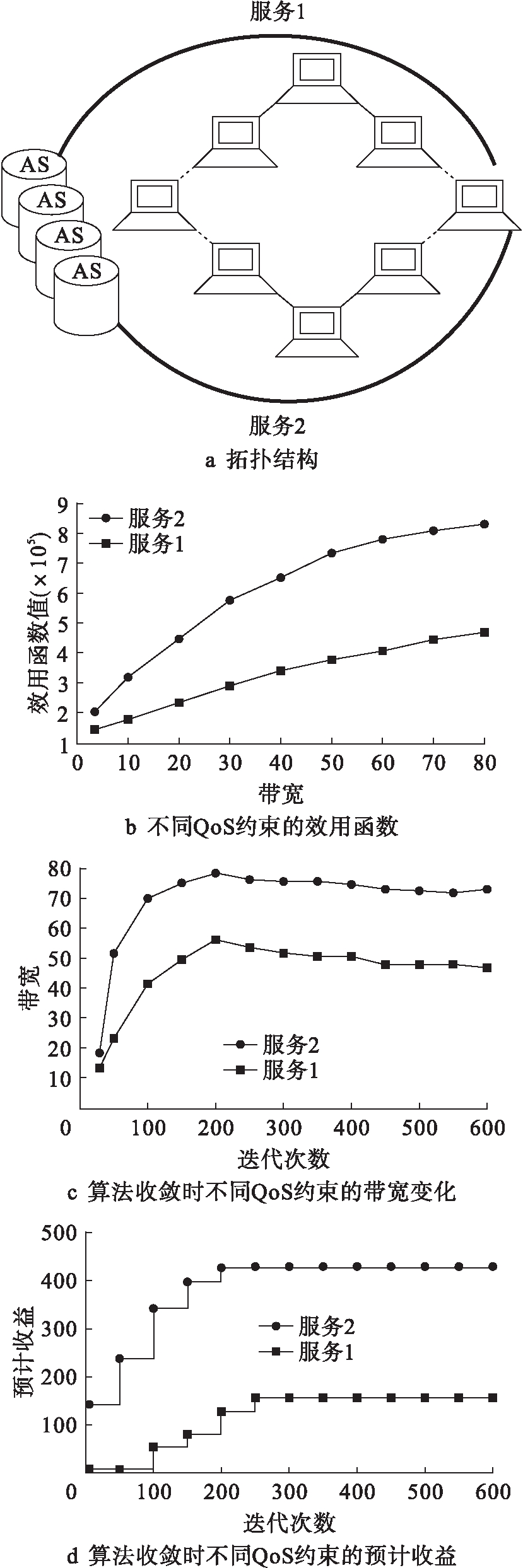
图1 算法应用实例的性能仿真结果
Fig.1 Performance simulation results foralgorithm application examples
定义1 Shapley值.给定一个联盟博弈(M,v),存在一个唯一的预归集φ(M,v)满足对称性、虚拟玩家和可加性,就把它称为Shapley值.对于玩家i来说,φ(M,v)可定义为
φi(M,v)![]()
[v(Q∪{i})-v(Q)]
(9)
2.2 收益分享
为了分享收益,设博弈中的玩家是联盟中N个AS的集合,假设对于每个服务来说,投标各自服从连续概率分布,把发生在一定时间内拍卖的效用函数用该时间内全部效用的平均值来表示,即
(10)
一般情况下,式(10)是as的一个严格的凹函数.假设每个AS的延迟函数在考虑的时间段内保持不变,则对于每个子联盟Q⊆N来说,价值函数v就可以作为问题3的解.
问题3:
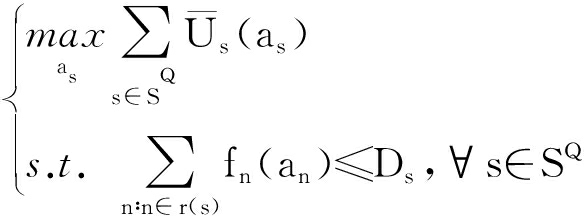
(11)
式中,SQ为由Q能够提供的服务的集合.一旦联盟收集到全部收益,在带宽分配阶段,收益就在全部AS之间按Shapley值的比例进行分享.
定理2 提高容量的激励机制.令(N,v,c)为一个联盟博弈,N个节点集代表博弈者,c表示N中全部节点的等效容量,v是由问题3定义的价值函数.如果增加节点i的容量,i∈N,则分享系数φi将不会减少.令c*为当i的容量增加时全部节点的容量,则φi(N,v,c*)≥φi(N,v,c),φi(N,v,c)给定博弈(N,v)和容量c中节点i的Shapley值.
根据Shapley值的定义,则有
φi(N,v,c*![]() ∪{i},c*)-
∪{i},c*)-
v(Q,c*)]
(12)
式中:K为常数;v(Q,c*)为当容量给定为c*时子联盟Q的价值函数.由于除i外(不考虑i的容量)任何联盟的价值函数是相同的,通过减去i的分享系数,则有
φi(N,v,c*)-φi(N,v,c)![]() ∪{i},c*)-
∪{i},c*)-
v(Q∪{i},c)]
(13)
事实上,v是问题3的解,是具有凸约束条件的凹函数的最大化值.通过增加容量,就会得到更大的或相等的解.
定理2表明,如果节点i增加其容量,则分享系数就会增加或保持不变,在所考虑的时间段内,联盟所预计的总收益也不会减少.因此,如果节点i的容量增加,那么联盟可以分配更多的带宽(使收益增加),或者可以分配相同数量的带宽(使收益保持不变).
2.3 分享机制性能仿真
为了体现基于Shapley值激励的收益分享机制的有效性,本文采用图2a所示的拓扑结构,并与采用一般Shapley值的联盟博弈算法进行比较.3个AS的容量以及延迟函数都是相同的,买家对各个AS的出价是随机的,故每个AS获得的收益是不同的.图2b为对于3个AS在本文提出的基于Shapley值激励的收益分享机制和采用一般Shapley值的联盟博弈算法得到的累计收益.本文提出的基于Shapley值激励的收益分享机制对于每个AS来说,其累计收益始终要高于采用一般Shapley值的联盟博弈算法得到的累计收益,3个AS的平均累计收益增加了约28%,说明本文提出的收益分享机制能够激励联盟中各个AS增加其容量,从而不仅增加整个联盟的累计总收益,而且各个AS的累计收益也明显增加,说明本文提出的收益分享机制是可行且可操作的.
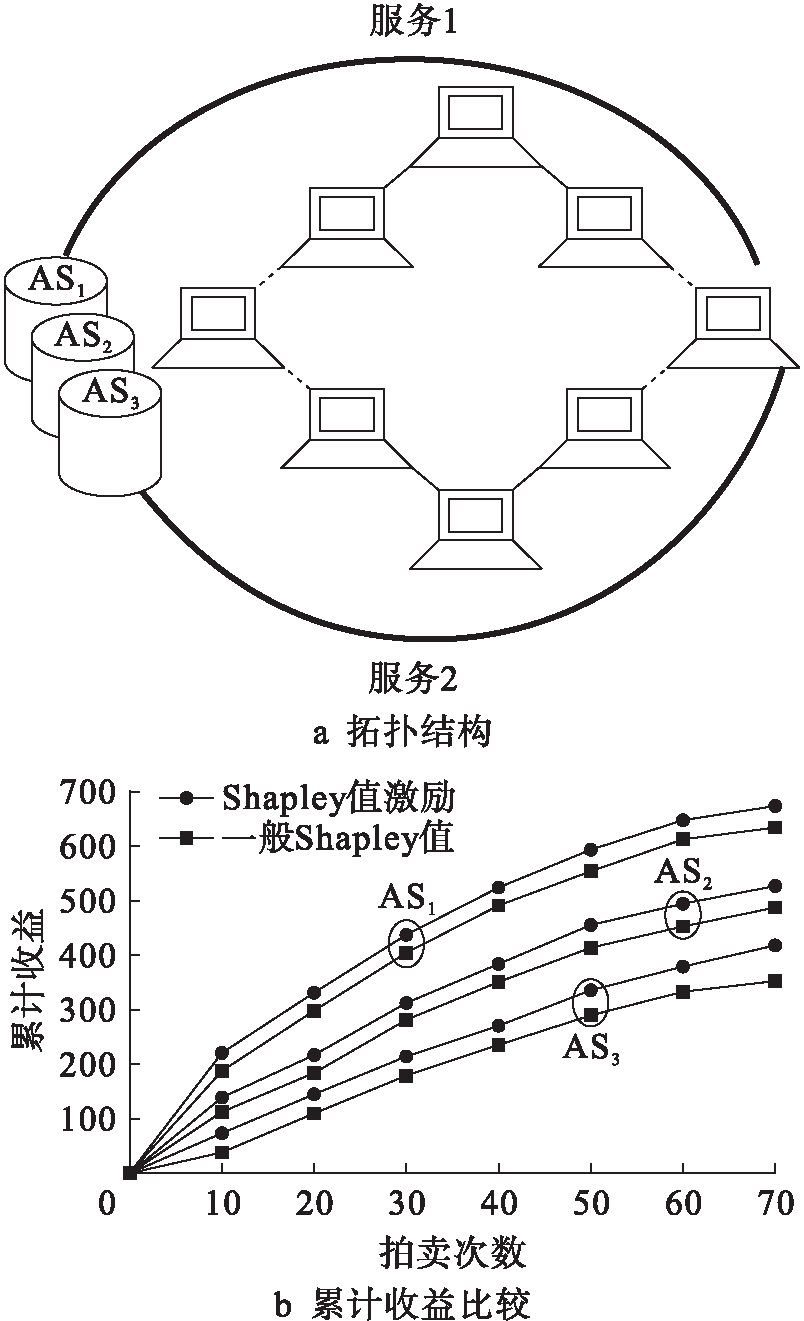
图2 不同收益分享机制下的累计收益比较
Fig.2 Comparison in cumulative income underdifferent income sharing mechanisms
3 结 论
本文提出了一种基于带宽优化分配的收益最大化算法和基于Shapley值激励的收益分享机制,分析了具有QoS约束的网络带宽分配问题,并以基于网络带宽拍卖应用为实例,将联盟博弈理论和Shapley值用于联盟收益分享,既能使整个联盟收益最大化,又能增加整个联盟的收益和其自身的收益分享.
参考文献(References):
[1] Trestian R,Ormond O,Muntean G M.Performance evaluation of MADM-based methods for network selection in a multimedia wireless environment [J].Wireless Networks,2015,21(5):1-19.
[2]蒲斌,崔梦天,赵海军.基于二阶段的3D虚拟世界客户分配方法 [J].计算机工程,2016,42(1):109-115.
(PU Bin,CUI Meng-tian,ZHAO Hai-jun.Client allocation approach in 3D virtual world based on two-stage [J].Computer Engineering,2016,42(1):109-115.)
[3] 王晗,吴心筱,贾云得.使用异构互联网图像组的视频标注 [J].计算机学报,2013,36(10):2062-2069.
(WANG Han,WU Xin-xiao,JIA Yun-de.Video annotation by using heterogeneous multiple image groups on the web [J].Chinese Journal of Computer,2013,36(10):2062-2069.)
[4] Douville R,Pouyllau H,Lonsethagen H.ETICS:QoS-enabled interconnection for future internet services [J].Frontiers in Psychology,2013,5(7):640.
[5] 段华琼,唐宾徽.基于线性多尺度模型的计算机网络数据流量预测 [J].沈阳工业大学学报,2017,39(3):322-327.
(DUAN Hua-qiong,TANG Bin-hui.Prediction of data flow in computer network based on linear multi-scale model [J].Journal of Shenyang University of Technology,2017,39(3):322-327.)
[6] 王思秀,郭文强,于凯,等.异构网络中支持终端直通的联合模式资源复用算法 [J].沈阳工业大学学报,2017,39(4):422-427.
(WANG Si-xiu,GUO Wen-qiang,YU Kai,et al.A resource reuse algorithm for device-to-device communication based on combination mode in heterogeneous networks [J].Journal of Shenyang University of Technology,2017,39(4):422-427.)
[7] Ma R T B,Chiu D M,Lui J C S,et al.Internet economics:the use of shapley value for ISP settlement [J].IEEE/ACM Transactions on Networking,2010,18(3):775-787.
[8] Courcoubetis C,Dramitinos M,Stamoulis G D,et al.Inter-carrier interconnection services:QoS,economics and business issues [J].Computers & Communications,2011,34(17):779-784.
[9] 张云鹤,朱艳琴,纪其进.基于拍卖的 P2P 内容分发网络带宽分配机制 [J].通信学报,2013,34(4):99-105.
(ZHANG Yun-he,ZHU Yan-qin,JI Qi-jin.Auction based bandwidth allocation mechanism for P2P content distribution networks [J].Journal on Communications,2013,34(4):99-105.)
[10]刘志新,申妍燕,关新平.一种基于VCG拍卖的分布式网络资源分配机制 [J].电子学报,2010,38(8):1929-1934.
(LIU Zhi-xin,SHEN Yan-yan,GUAN Xin-ping.A VCG-auction based distributed mechanism for network resource allocation [J].Acta Electronica Sinica,2010,38(8):1929-1934.)
[11]Vohra R V.Combinatorial auctions [J].Handbook of Game Theory with Economic Applications,2015,4(1):455-476.
[12]Shin K,Jung J Y,Lee J R.Resource allocation and pricing mechanisms for wireless multimedia service:auction and bargaining models [J].Journal of Internet Technology,2013,14(7):1093-1103.
[13]Canzian L,Xiao Y,Zorzi M,et al.Game theoretic design of MAC protocols:pricing and intervention in slotted-Aloha [J].IEEE Transactions on Communication,2013,63(11):4287-4303.
[14]Belzarena P,Paganini F,Ferragut A.Optimizing revenue for bandwidth auctions over networks with time reservations [J].Computer Networks,2011,55(9):2289-2302.