控制工程
贺 琳1, 白朝阳2
(1. 大连海事大学 交通运输管理学院, 辽宁 大连 116026; 2. 大连理工大学 管理与经济学部, 辽宁 大连 116023)
摘 要: 针对云制造服务链稳定问题,提出了单一制造商同供应商联盟进行谈判的二阶段领导者![]() 追随者博弈模型.该模型根据云制造实际情境,假设制造商决定订单或服务的数量和价格,将云制造过程中制造商与供应商的合作过程抽象为两阶段的博弈,其中第一阶段为面向供应商联盟的竞争博弈,第二阶段为制造商同供应商联盟的合作博弈,并分析了合作策略选择机理.模型分析结果表明,优质供应商个体采用联盟形式,可以获得更高议价权和利益,并可对保持云制造服务链的稳定发展提供一定的决策支持.
追随者博弈模型.该模型根据云制造实际情境,假设制造商决定订单或服务的数量和价格,将云制造过程中制造商与供应商的合作过程抽象为两阶段的博弈,其中第一阶段为面向供应商联盟的竞争博弈,第二阶段为制造商同供应商联盟的合作博弈,并分析了合作策略选择机理.模型分析结果表明,优质供应商个体采用联盟形式,可以获得更高议价权和利益,并可对保持云制造服务链的稳定发展提供一定的决策支持.
关 键 词: 制造商; 供应商; 联盟; 合作竞争博弈; 领导者![]() 追随者博弈; 谈判; 云制造; 制造服务
追随者博弈; 谈判; 云制造; 制造服务
云制造是一种基于网络并面向服务的智慧化制造新模式,基于云计算、物联网、服务计算、智能科学和高效能计算等新兴信息技术,云制造将各类制造资源和制造能力进行虚拟化、服务化,构成制造资源和制造能力的服务云池,并进行统一、集中的优化管理和经营,从而完成制造全生命周期的各类活动[1].作为一种新的制造模式,云制造的主要特征是实现制造资源与制造能力的开放和共享.核心制造商和多个供应商构成了云制造供应链,与传统供应链相比,云制造供应链个体具有更加灵活的进入自主性.如何构建稳定的供应链是目前云制造供应链研究的热点问题.
国内外已有一些学者探讨了供应链上制造商与其供应商之间的博弈问题.Marx等首先探讨了单个制造商与双供应商之间依次谈判的多边谈判模型,结果表明,当供应商处于不同的谈判地位与制造商进行博弈时,供应商讨价还价能力的不同会对其所获得的利润产生不同影响[2-3].付娟等研究了供应链中零售商与供应商之间的一体化博弈与协调问题,根据制造商同时决策和先后决策的情景建立了Nash均衡博弈以及Stackelberg主从博弈模型,并分析了供应商行为对供应链各方利润变化的影响[4].Ang等研究了单一制造商作为追随者以及多个供应商作为领导者的供应链优化问题,在确定采购原料价格的前提下供应商之间针对配送频率进行竞争,博弈的目标在于追求单个供应商利润的最大化以及制造商采购成本的最小化,并利用变分不等式证明了最优解的存在性和唯一性[5].Demiguel等构建了针对供应一种同质产品(或服务)进行博弈的随机多领导者Stackelberg博弈模型,研究发现供应商角色不同,其市场影响力也不同,且追随者比领导者更具有市场竞争力[6].慕静等从道德风险角度建立了供应链同级企业之间的道德风险演化博弈模型以及供应链网络上下游企业间的道德风险演化SD模型[7].刘强等构建了单买方与具有不同讨价还价能力的多个供应商分别进行双边谈判或多边谈判的博弈模型,并指出供应商数量及其讨价还价能力是影响其承诺战术的重大因素[8].江世英等以一个制造商和一个零售商组成的二级绿色供应链为背景,建立了考虑产品绿色度的4种绿色供应链博弈模型,通过比较分析4种博弈模型下的产品绿色度、产品价格与批发价格,建立了收益共享契约下的博弈模型[9].张国兴等研究了双渠道模式下制造商和零售商在不同权利结构下的博弈模型,探讨了不同形式下博弈模型对渠道价格、产品需求及博弈参与者利润的影响[10].肖迪等以两个供应商和一个制造商构成的二级供应链为背景,研究了在质量和价格竞争同时作用下的供应链协调机制[11].李凤艳针对由一个供应商与两个制造商组成的供应链系统模型,在产品单一定价与差别定价两种情境下,以实现供应链整体利润最大化为目标,建立了供应链最优控制模型[12].
以往文献在研究制造商与其供应商之间的博弈时只考虑了供应商之间完全竞争的情况,忽略了供应商为了获得更大收益而进行合作的情形.实际上,在制造商实力强大,供应商数量众多、实力不同的情况下,为了获得更高利润,供应商有必要进行合作,以增强整体实力,并通过竞争分配所获收益.制造商及其供应商作为供应链上的供需双方存在产品或服务的买卖关系[13-14].云环境下制造资源通过云计算、物联网等技术接入互联网并形成云服务,因而信息传递更加快捷,信息共享程度更高,供应链的组织方式更为灵活,企业进出供应链更加自由,这就为供应商之间的合作竞争创造了有利条件[15-17],并为企业实现获取最大利润提供了可能.鉴于此,本文根据云制造实际运作情境,从核心制造商与供应商联盟博弈角度,系统考虑了云制造环境(简称云环境)下供应商之间的合作竞争关系,研究了制造商与供应商的合作过程和策略选择的内在机理,建立了制造商同供应商联盟进行谈判的领导者![]() 追随者博弈模型,对比分析了供应商之间合作与不合作两种情形对其收益的影响,以期为构建稳定发展的良性云制造环境提供决策支持.
追随者博弈模型,对比分析了供应商之间合作与不合作两种情形对其收益的影响,以期为构建稳定发展的良性云制造环境提供决策支持.
传统供应链制造商与供应商的关系如图1所示.由图1可见,在传统供应链下制造商为了降低对单个供应商的依赖程度并降低风险,会选择多个供应商供应其需求,而供应商之间重在竞争,缺乏交流,在与强大的制造商进行谈判时往往处于劣势地位,从而被动地接受制造商提出的订单需求.
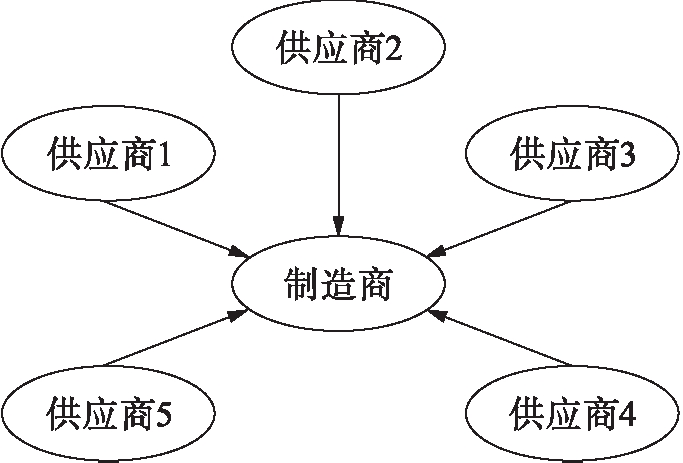
图1 传统供应链制造商与供应商的关系
Fig.1 Relationship between traditional manufacturerand suppliers of supply chain
随着科学技术的进步,云制造为供应商提供了相互交流的平台.为了增强与制造商进行讨价还价的能力,供应商可以联合起来,结盟应对制造商提出的订单需求.云制造下制造商与供应商的关系如图2所示.由图2可见,具有相同条件的供应商之间可以通过云制造模式形成短期联盟,在订单完成之后,可以选择解散或者继续合作下一个订单,从而增强了供应商谈判的综合实力.由于企业进出灵活,一个供应商可以根据不同的订单与不同的供应商形成多个联盟,对供应商自身而言,不仅降低了依赖一个供应商联盟的风险,而且提高了自身的讨价还价能力.
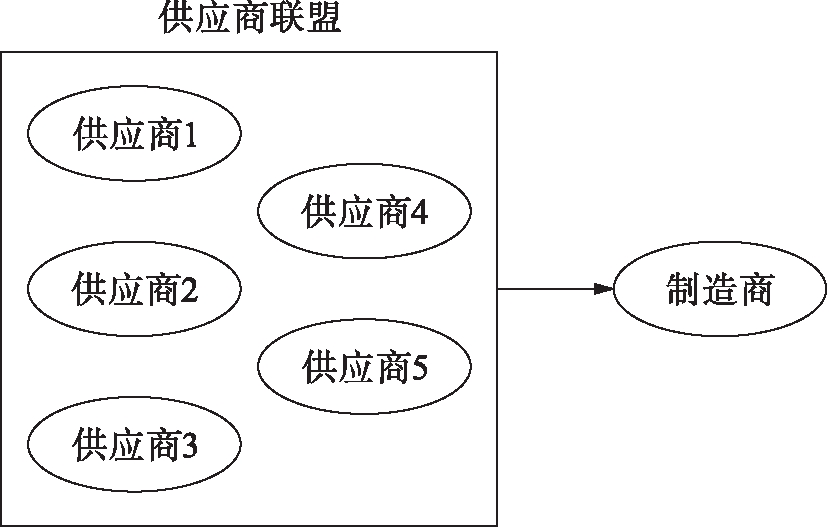
图2 云制造下制造商与供应商的关系
Fig.2 Relationship between manufacturer andsuppliers under cloud manufacturing
对于供应商而言,选择加入或拒绝联盟是一个选择最大效用的问题.本文建立了云制造下制造商同供应商联盟谈判的二阶段领导者![]() 追随者博弈模型,研究了供应商在联盟中获得的效用是否大于单独与供应商谈判获得的效用的问题.模型情境为云制造下N个供应商为一大型制造商提供一种同质的原料(半成品或零部件,以下用物料代替),但是不同供应商的供应量、生产成本与运输成本等存在差别.供应商联盟与制造商谈判的过程由两阶段组成.在第一阶段,具有共同目标的供应商通过合作竞争博弈形成供应商联盟,单个供应商通过合作方式增加同制造商谈判的实力,并利用竞争分配获得利润;在第二阶段,供应商联盟根据制造商对该种物料的需求量,同制造商谈判确定所供应物料的价格.
追随者博弈模型,研究了供应商在联盟中获得的效用是否大于单独与供应商谈判获得的效用的问题.模型情境为云制造下N个供应商为一大型制造商提供一种同质的原料(半成品或零部件,以下用物料代替),但是不同供应商的供应量、生产成本与运输成本等存在差别.供应商联盟与制造商谈判的过程由两阶段组成.在第一阶段,具有共同目标的供应商通过合作竞争博弈形成供应商联盟,单个供应商通过合作方式增加同制造商谈判的实力,并利用竞争分配获得利润;在第二阶段,供应商联盟根据制造商对该种物料的需求量,同制造商谈判确定所供应物料的价格.
模型建立的假设条件为:
1) 供应商可以通过云制造平台沟通交流,且付出成本忽略不计;
2) 制造商的需求量D服从正态分布;
3) 由制造商制定采购配额,每个供应商对该物料的供应量为λi.
模型建立过程中主要参数说明:
1) 供应商i∈N的生产变动成本为ci,单位运输成本为ki,物料的交易价格为p;
2) rj(j=1,2)表示制造商和供应商联盟的策略选择;
3) u(rj)(j=1,2)表示制造商和供应商联盟的效用函数.
首先建立第一阶段供应商合作竞争博弈联盟模型.制造商的需求量的数学期望E(D)可以表示制造商的平均需求.供应商联盟的形成过程建立在单个供应商成员偏好的基础上,并以竞争(非合作)博弈作为微观基础.每一个供应商即为一个合作竞争博弈的参与人.合作竞争博弈的核心是所有参与人找到自己所有策略组合下的最小效用系数,然后从中选择相对较大的效用系数,则该效用系数对应的策略即为合作竞争博弈的均衡策略,若选择该策略的参与人最多,则参与人达到均衡状态.每个参与人的效用系数为该参与人在该策略下的效用与其所能获得最大效用的比值.
若供应商i的生产变动成本函数ci(λi)=ciλi,则相应物料的线性逆需求函数可以表示为
p(λ)=E(D)-(λ1+…+λi+…+λn)
(1)
供应商i的利润函数,即目标函数可以表示为
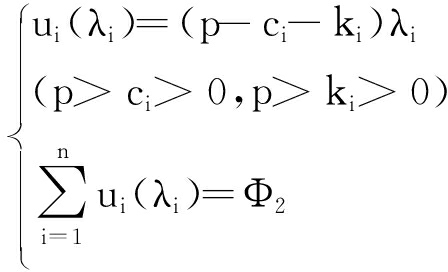
(2)
式中:ui(λi)为供应商效用;Φ2为供应商联盟与制造商博弈获得的总效用.
利用供应商效用系数来表示供应商利益,且该效用系数为供应商效用与最大效用的比值.供应商i需要通过合作竞争来使效用系数最大化.供应商、供应量决策、供应量与利润分别对应博弈中的参与人、策略选择、结果和效用.当供应商i垄断市场时,所获得的效用最大,且该最大效用可以表示为
![]() /4
/4
(3)
因此,供应商i的效用系数可以表示为
Qi(λi)= ui(λi)/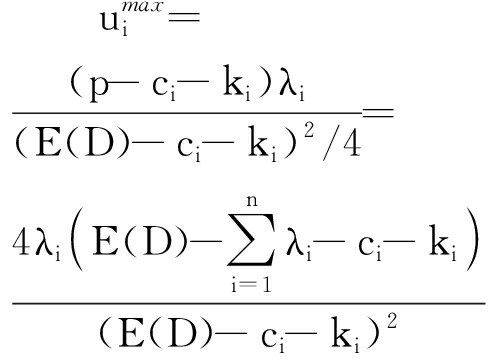
(4)
Ang等已经证明由制造商制订采购配额的分配策略且供应商之间就配送频率进行竞争的两阶段博弈模型的均衡解是存在且唯一的[5].在供应商联盟与制造商的博弈中,制造商为领导者,供应商联盟为追随者.制造商决定特定物料的需求量,制订需求策略;供应商联盟在制造商制订的需求计划基础上,决定所供应物料的价格策略.制造商在制订需求策略时需要充分了解供应商联盟如何行动,即供应商联盟的反应函数.
随后需要建立第二阶段制造商与供应商联盟针对所供应物料价格的领导者![]() 追随者博弈模型.利用Rj(j=1,2)表示制造商和供应商联盟的策略空间,给定制造商的选择策略后,供应商联盟的目标函数可以表示为
追随者博弈模型.利用Rj(j=1,2)表示制造商和供应商联盟的策略空间,给定制造商的选择策略后,供应商联盟的目标函数可以表示为
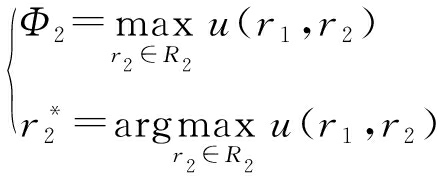
(5)
式中,![]() ,上述问题的最优解.
,上述问题的最优解.
根据Stackelberg模型,制造商制订需求计划前能够观察到供应商联盟的反应函数,即供应商联盟的策略选择最优解![]() ,因此,制造商可以通过选择相应的策略r1,使得自身效用最大化,此时对应的目标函数可以表示为
,因此,制造商可以通过选择相应的策略r1,使得自身效用最大化,此时对应的目标函数可以表示为
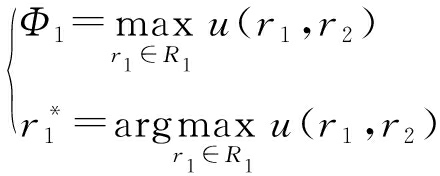
(6)
式中:Φ1为制造商的效用;![]() 为相应问题的最优解.此时,供应商联盟与制造商两阶段博弈的最优解可以表示为
为相应问题的最优解.此时,供应商联盟与制造商两阶段博弈的最优解可以表示为![]() ,
,![]() .
.
对于有限合作竞争博弈而言,可以使用枚举法将满足目标函数的可行解即供应商i的最低效用系数一一列出,再从中选择最大的效用系数,即可获得最优解.对于效用函数可导的无限合作竞争博弈而言,可以转化为非线性规划问题,并利用拉格朗日乘子和Karush-Kuhn-Tucker(KKT)条件进行求解.
为了求解供应商联盟内部合作竞争博弈的均衡解,根据Minimax定理求解![]() λ1),Q2(λ2),…,Qn(λn)),结合式(4)可得相应求解表达式为
λ1),Q2(λ2),…,Qn(λn)),结合式(4)可得相应求解表达式为
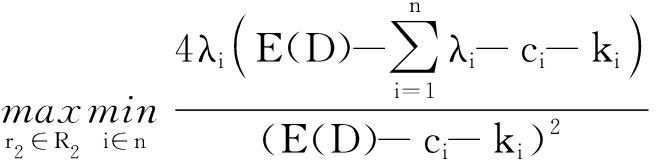
(7)
将式(7)转化为等价非线性规划问题进行求解,且等价非线性规划表达式为
max H
(8)
式中,H≤![]() .
.
由于Qi(λi)满足严格凸性并且是可行的,因此,λi最优解与拉格朗日乘子βi可以转化为Lagrange函数,即
L(H,![]() βi
βi![]() E(D)-
E(D)-
(9)
式中,![]() βi=1且βi≥0.
βi=1且βi≥0.
根据KKT条件,令式(9)对λi的偏导数为零,则
∂L/∂![]() βiλi+
βiλi+
βi(E(D)-ci-ki)=0
(10)
整理可得
(11)
若![]() λi-E(D)-ci-ki=0,代入式(4)可知Qi(λi)=0,即每个供应商联盟成员的效用系数均为零,不符合实际情况,因而不会被任何一个联盟成员所采纳.
λi-E(D)-ci-ki=0,代入式(4)可知Qi(λi)=0,即每个供应商联盟成员的效用系数均为零,不符合实际情况,因而不会被任何一个联盟成员所采纳.
若nβi-1=0,则βi=1/n.结合式(4)和(10)可知,![]() ,此时供应商联盟合作竞争博弈均衡点处所有供应商的效用系数相同,即Q1(λ1)=Q2(λ2)=…=Qn(λn)=max H,经过相应计算可知,此时均衡点处供应商i的效用系数Qi(λi)=1/n.此外,均衡点处供应商i获得的效用可以表示为
,此时供应商联盟合作竞争博弈均衡点处所有供应商的效用系数相同,即Q1(λ1)=Q2(λ2)=…=Qn(λn)=max H,经过相应计算可知,此时均衡点处供应商i的效用系数Qi(λi)=1/n.此外,均衡点处供应商i获得的效用可以表示为
(12)
若供应商之间进行完全竞争,并单独同制造商进行谈判,则此时供应商i获得的效用为
ui(λi)′![]()
(13)
由于ui(λi)>ui(λi)′,因此,相对于完全竞争而言,供应商之间合作竞争获得的效用更大.
假设两个供应商同时为某制造商提供所需物料,若制造商所需物料的期望E(D)=5,c1=2,c 2=1,k1=k2=1,则两个供应商的供应量之间的关系可以表示为
![]() λ1λ2-18λ1+12λ2=0
λ1λ2-18λ1+12λ2=0
(14)
式中:λ1∈[0,2];λ2∈[0,3].
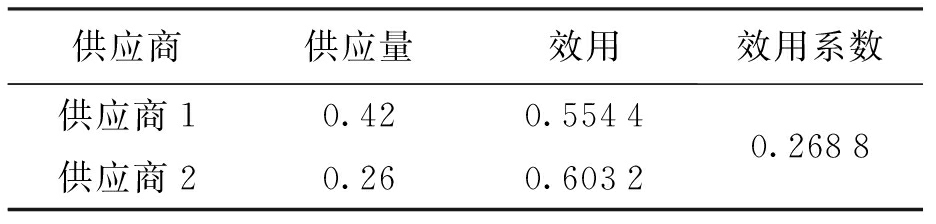
利用计算机求解近似解,得到的1 000等分精度下的效用系数模拟结果如图3所示.表1为1 000等分精度下的均衡战略与均衡效用数据.由表1可见,精度为0.001的均衡点处两个供应商的供应量分别为0.42和0.26,均衡点处的效用分别为0.554 4和0.603 2,均衡点处的效用系数为0.268 8.若供应商之间采用完全竞争方式单独同制造商进行谈判,则可获得的效用分别为0.222与0.333,可见供应商联盟所获效用明显高于单独同制造商谈判时获得的效用.
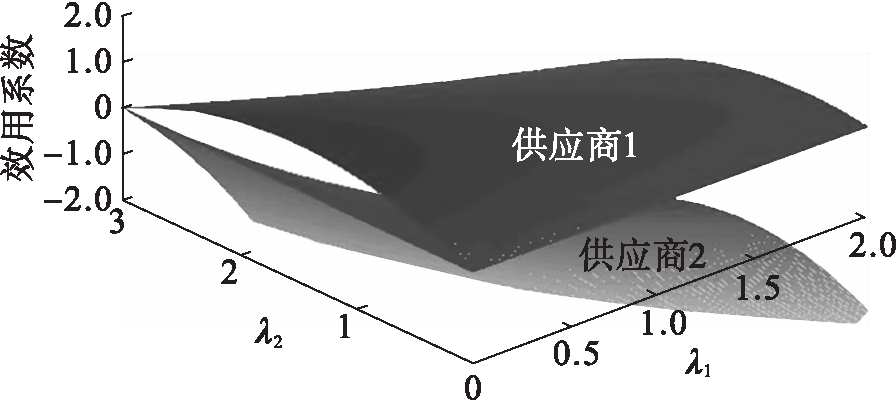
图3 1 000等分精度下的效用系数图
Fig.3 Utility coefficient diagram with precisionat level of 1 000 aliquots表1 1 000等分精度下的均衡战略与均衡效用
Tab.1 Balance strategy and utility with precisionat level of 1 000 aliquots
由以上模型分析可知,当多个供应商选择联盟策略时,其产生的利益要远大于单独向制造商供货产生的利益,从本质上讲,供应商联盟削弱了制造商作为价格主导者的地位,提高了供应商与制造商讨价还价的能力.
本文从供应商角度,研究了单一制造商同多个供应商之间的领导者![]() 追随者博弈,以及供应商联盟内部的合作竞争博弈.通过将供应商联盟内部合作竞争博弈与由完全竞争获得的效用进行对比后发现,供应商联盟内部采用合作竞争策略有利于提高每个供应商获得的效用,对供应商而言更具吸引力,这种联盟式的供应商群体在满足制造商需求时,更为灵活快捷,更具优越性,因而为供应商之间寻求合作联盟提供了理论基础.但从长远来看,制造商为了降低采购风险,一贯采取的战略方式为多家供应商并存,因而会在一定程度上发展一定数量的其他供应商[13],当多家供应商联盟之后,制造商失去主动优势,就可能会寻找可替代的供应商,并在两者成本之间进行取舍.因此,供应商之间不能仅限于简单的供应叠加式合作,而应该在零件或半成品的质量提升方面进行长远合作,充分利用云制造环境的优势,取长补短,增强核心竞争力,这对于供应链上其他企业的发展也同样具有深远意义.
追随者博弈,以及供应商联盟内部的合作竞争博弈.通过将供应商联盟内部合作竞争博弈与由完全竞争获得的效用进行对比后发现,供应商联盟内部采用合作竞争策略有利于提高每个供应商获得的效用,对供应商而言更具吸引力,这种联盟式的供应商群体在满足制造商需求时,更为灵活快捷,更具优越性,因而为供应商之间寻求合作联盟提供了理论基础.但从长远来看,制造商为了降低采购风险,一贯采取的战略方式为多家供应商并存,因而会在一定程度上发展一定数量的其他供应商[13],当多家供应商联盟之后,制造商失去主动优势,就可能会寻找可替代的供应商,并在两者成本之间进行取舍.因此,供应商之间不能仅限于简单的供应叠加式合作,而应该在零件或半成品的质量提升方面进行长远合作,充分利用云制造环境的优势,取长补短,增强核心竞争力,这对于供应链上其他企业的发展也同样具有深远意义.
参考文献(References):
[1] 齐二石,李天博,刘亮,等.云制造理论、技术及相关应用研究综述 [J].工业工程与管理,2015,20(1):8-14.
(QI Er-shi,LI Tian-bo,LIU Liang,et al.The review of cloud manufacturing theory,technologies and application states [J].Industrial Engineering and Management,2015,20(1):8-14.)
[2] Marx L,Shaffer G.Break-up fees and bargaining power in sequential contracting [J].International Journal of Industrial Organization,2010,28(5):451-463.
[3] Marx L,Shaffer G.Rent shifting and the order of negotiations [J].International Journal of Industrial Organization,2007,25(5):1109-1125.
[4] 付娟,闵杰,赵菊,等.基于需求依赖库存的多制造商供应链博弈与协调模型 [J].管理工程学报,2016,30(3):195-201.
(FU Juan,MIN Jie,ZHAO Ju,et al.Game and coordination models for supply chain with multiple manufacturers under inventory-dependent demand [J].Journal of Industrial Engineering and Engineering Management,2016,30(3):195-201.)
[5] Ang J,Fukushima M,Meng F W,et al.Establishing Nash equilibrium of the manufacturer-supplier game in supply chain management [J].Journal of Global Optimization,2013,56:1297-1312.
[6] Demiguel V,Xu H F.A stochastic multiple-leader Stackelberg model:analysis,computation and application [J].Operations Research,2009,57:1220-1235.
[7] 慕静,毛金月.供应链网络道德风险演化与仿真研究 [J].运筹与管理,2013,22(4):68-76.
(MU Jing,MAO Jin-yue.A study on evolution and simulation of moral hazard in supply chain networks [J].Operations Research and Management Science,2013,22(4):68-76.)
[8] 刘强,苏秦.供应链多边谈判中的买方承诺战术 [J].系统工程学报,2012,27(2):243-247.
(LIU Qiang,SU Qin.Buyer’s commitment tactic in supply chain multilateral negotiation [J].Journal of Systems Engineering,2012,27(2):243-247.)
[9] 江世英,李随成.考虑产品绿色度的绿色供应链博弈模型及收益共享契约 [J].中国管理科学,2015,23(6):169-176.
(JIANG Shi-ying,LI Sui-cheng.Green supply chain game models and revenue sharing contract with product green degree [J].Chinese Journal of Management Science,2015,23(6):169-176.)
[10]张国兴,方帅,汪应洛.不同权力结构下的双渠道供应链博弈分析 [J].系统工程,2015(3):52-59.
(ZHANG Guo-xing,FANG Shuai,WANG Ying-luo.Game analysis in a dual-channel supply chain with different power structures [J].Systems Engineering,2015(3):52-59.)
[11]肖迪,袁敬霞,包兴.质量与价格双重竞争情景下的供应链协调策略分析 [J].中国管理科学,2013,21(4):82-88.
(XIAO Di,YUAN Jing-xia,BAO Xing.Supply chain coordination strategy considering dual competition from price and quality [J].Chinese Journal of Mana-gement Science,2013,21(4):82-88.)
[12]李凤艳.供应链中间产品转移价格最优控制 [J].沈阳工业大学学报,2015,37(4):451-455.
(LI Feng-yan.Optimal control on transfer price of intermediate products in supply chain [J].Journal of Shenyang University of Technology,2015,37(4):451-455.)
[13]古川,张红霞,安玉发.云制造环境下的供应链管理系统研究 [J].中国科技论坛,2013(2):122-127.
(GU Chuan,ZHANG Hong-xia,AN Yu-fa.On supply chain management system in cloud manufacturing environment [J].Forum on Science and Technology in China,2013(2):122-127.)
[14]刘会燕,戢守峰.考虑产品绿色度的供应链横向竞合博弈及定价策略 [J].工业工程与管理,2017,22(4):91-99.
(LIU Hui-yan,JI Shou-feng.Horizontal competition cooperation game and pricing strategy of supply chain considering product green degree [J].Industrial Engineering and Management,2017,22(4):91-99.)
[15]刘军,谭德庆,李良.供应链价格策略与主导模式博弈分析 [J].软科学,2017,31(4):132-138.
(LIU Jun,TAN De-qing,LI Liang.Game analysis of supply chain price strategy and leading mode [J].Soft Science,2017,31(4):132-138.)
[16]钱奕凡.供应链网络节点间信息共享的演化博弈分析 [J].网络安全技术与应用,2017(3):63-64.
(QIAN Yi-fan.Evolutionary game analysis of information sharing among supply chain network nodes [J].Network Security Technology & Application,2017(3):63-64.)
[17]何丽红,廖茜,刘蒙蒙,等.两层供应链系统最优广告努力水平与直接价格折扣的博弈分析 [J].中国管理科学,2017,25(2):130-138.
(HE Li-hong,LIAO Qian,LIU Meng-meng,et al.Game analysis of optimal advertising effort level and direct price discount for two-tier supply chain system [J].Chinese Journal of Management Science,2017,25(2):130-138.)
HE Lin1, BAI Zhao-yang2
(1. Transportation Management College, Dalian Maritime University, Dalian 116026, China; 2. Faculty of Management and Economics, Dalian University of Technology, Dalian 116023, China)
Abstract: Aiming at the stability problem of cloud manufacturing service chain, a two-stage leader-follower game model for the negotiation between the single manufacturer and supplier union was established. According to the actual situation of cloud manufacturing, it was assumed in the model that the manufacturer decided the quantity and price of orders or services, and the cooperation process between the manufacturer and suppliers in the cloud manufacturing process was abstracted as a two-stage game. The first stage was the competition game facing to the supplier union. The second stage was the cooperative game between the manufacturer and supplier union, and the selection mechanism of cooperation strategy was analyzed. The results of model analysis indicate that the individual supplier with high quality adopts the alliance form to obtain higher bargaining power and benefit, which has a certain decision support to maintain the stable development of service chain under the cloud manufacturing.
Key words: manufacturer; supplier; union; competitive and cooperative game; leader-follower game; negotiation; cloud manufacturing; manufacturing service
收稿日期: 2017-07-12.
基金项目: 中央高校基础科研业务资助项目(3132017086); 教育部人文社会科学研究青年基金资助项目(13YJCZH052); 辽宁省社科规划资助项目(L15BGL040).
作者简介: 贺 琳(1980-),女,江西吉安人,副教授,博士,主要从事智能制造信息化技术与物流交通系统等方面的研究.
* 本文已于2018-05-03 13∶03在中国知网优先数字出版.
网络出版地址:http:∥kns.cnki.net/kcms/detail/21.1189.T.20180503.0901.018.html
doi:10.7688/j.issn.1000-1646.2018.03.16
中图分类号: TM 343
文献标志码:A
文章编号:1000-1646(2018)03-0328-06
(责任编辑:尹淑英 英文审校:尹淑英)