基于神经网络算法的网络安全评价模型*

摘　要：为了准确地评价复杂网络的信息安全水平，设计了一个具有网络安全评价功能的GABP算法评价模型.该模型通过引入德尔菲法等方法，建立了科学的评价指标体系.基于这一体系，通过修改BP算法和遗传算法的若干步骤，选取适当的目标函数，并对算法的流程进行精确控制，最终得到了一个具备这两种算法优点的GABP评价算法.该评价算法的仿真结果表明，只需输入复杂网络的信息安全监测数据，算法就可以准确评价出该网络的信息安全水平.

关　键　词：神经网络算法；遗传算法；德尔菲法；信息安全；安全评价； Matlab软件；目标函数；适应度

当前，各种计算机病毒、木马和黑客入侵等事件接连发生，网络信息安全的局势越来越严峻.在复杂的网络环境中，如何评价和检测网络的安全风险程度，成为了信息安全领域的重要问题.很多专家和学者做出了大量的努力[1-3]，这些算法的优点在于从各个角度对网络的安全状态进行了研究，但其缺点是实用性不强.为进一步优化网络安全评价模型，回避BP神经网络算法收敛慢、搜索能力差等问题，本文引入了GA遗传算法，得出了结合这两种算法的网络安全评价模型，该模型既克服了BP神经网络算法和GA遗传算法的缺点，同时兼具这两种算法的优点，能够理想地完成网络安全评价工作.

1　评价指标设计

在复杂网络环境中，公众信息安全受到了多方面威胁，例如恶意攻击、软件漏洞、软件后门和操作失误等.为了能够准确地评估网络安全受威胁的程度，需要建立起一套综合评价指标体系.

1.1　评价指标种类

评价指标需要从层次结构、安全特性和系统安全评价体系等角度进行讨论[4].首先，目前网络的层次结构大多都是TCP/IP协议的分层模型，应用层负责用户的应用程序，其安全措施包括个人认证、加密和签名等；传输层负责用户端的进程通信，使用了安全套接字、访问控制和加密等技术；网络层负责网络的路由服务，使用了防火墙、IPSec技术；链路层负责网络中点到点的通信服务，主要用加密技术来保障安全；物理层负责实现网络中的物理连接，使用了数据流加密技术等安全措施.其次，网络的安全特性主要包括数据的保密性、完整性、可用性、可控性和不可否认性，数据的保密性是指未授权的第三方不能取得该数据；完整性保护网络中真实信息不被未授权的第三方修改；可用性能够防止人为因素对网络信息的破坏；可控性是指对内部的信息和信息系统进行监管，防止恶意代码的执行和破坏；不可否认性是指对授权的用户行为进行监控，防止用户否认自己的行为[5].最后，网络安全的评价体系主要由网络的管理安全、环境安全、硬件安全、软件安全和数据安全等方面组成，这些大的方面可以囊括网络安全的各个具体评价指标，如入侵检测和访问控制等检测指标.

1.2　设计原则

1) 完备性.网络安全评价指标应该全面、完整和有效刻画出网络安全的基本特征，得出精确可信的评价结果.

2) 独立性.评价指标之间经常会有或多或少的相关性，设计人员应该尽量减少多个指标的联系，提高评价的准确性.

3) 简要性.优良的评价指标能够简明扼要地反映网络的安全水平.

4) 可操作性.指标设计必须切合实际，涉及数据的收集和处理过程简单易行.

1.3　评价指标体系

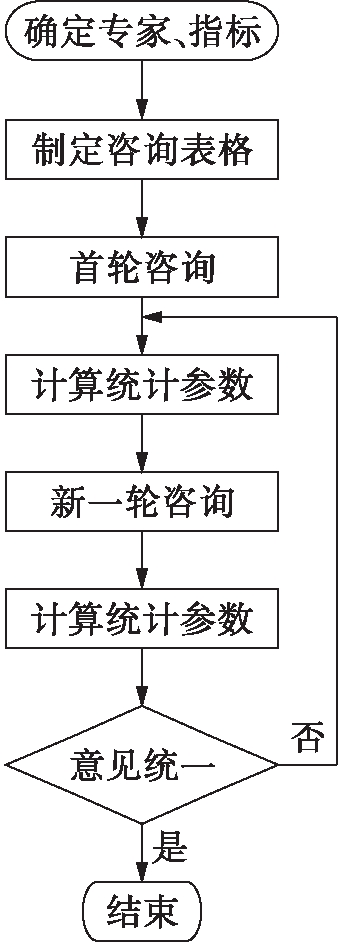
为建立科学的评价指标体系，本文引入了德尔菲法(Delphi)，该方法使用了背对背的方式咨询专家小组的意见，小组成员匿名发表意见，同时成员之间不允许相互讨论，通过这样多轮的反复询问和反馈修正，得到集中的预测意见，从而总结出符合实际情况的预测结论.这种方法也叫专家意见法，具有匿名性、反馈性和优良的统计特性，能够结合多个专家主观意见和客观规律，可以对大量无法定量分析的指标进行相对准确的估算.首先确定专家小组的所有成员和若干评价指标，制作出成员需要填写的咨询表格，然后进行首轮初步咨询，并计算需要统计的参数，进行多轮咨询并反复修正专家意见，最后统一专家成员的意见，本文使用德尔菲法流程图如图1所示[6].

图1　德尔菲法流程图
Fig.1　Flow chart of Delphi method

在德尔菲法的作用下，经过系统分析和对专家评分的统计，选取出的指标形成了本文评价模型的完整指标体系，该体系结构如图2所示.

2　算法模型

神经网络(BP)算法是一种借鉴人体神经元结构来进行信息处理和计算的智能算法，具有高度的自组织性和自学习性等优点，善于处理推理、判断等问题，但该算法也存在收敛速度慢、容易陷入局部极小值和网络泛化能力差等缺点[7-8].为了避免BP算法的上述缺陷，本文引入了GA遗传算法，将这两种算法结合到一起来进行计算，并对网络的安全程度进行计算和评价.在算法中，令E为目标函数，w和v分别为输入层到隐含层、隐含层到输出层的权值矩阵，θ和r分别为对应的阈值矩阵，m为输入层的数量，n为输出层的数量，p为隐含层的数量，则GABP算法的数学表达式为

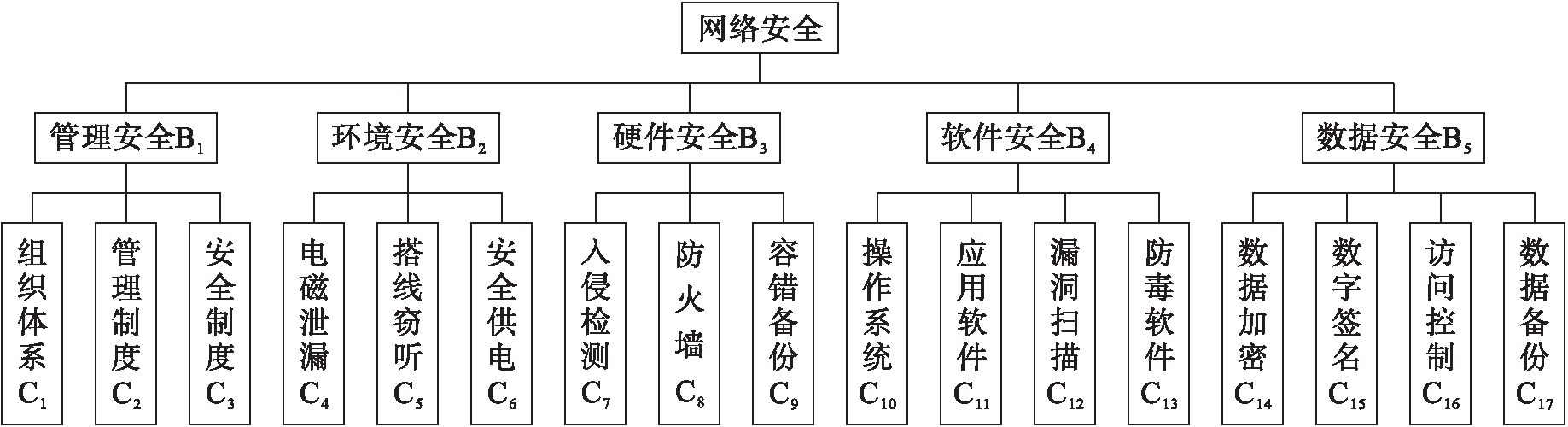
图2　网络安全评价指标体系
Fig.2　Network security evaluation index system

如上所述，GABP算法的输入层x∈Rm，输出层y∈Rn，输入层到隐含层的权值矩阵w∈Rm×p，阈值矩阵为θ∈Rp，隐含层到输出层的权值矩阵v∈Rp×n，阈值矩阵为r∈Rn.设隐含层h∈Rp，则输入层到隐含层的关系为h=xiwi+θi，且隐含层到输出层的关系为y=hvi+ri.其中，算法需要优化的对象是w、θ、v和r.

2.1　目标函数

在本算法中，目标函数被用来评价解的质量，将直接影响到算法的执行效率和运行结果.令yk(t)和

分别表示第t个节点的输出值和期望输出值，则本文目标函数E的表达式为

GABP算法的初始化需要使用BP神经网络算法中的反向传播算法来完成，令前向反馈结构的神经网络第l层第j个节点的输入为

输出为

反馈函数为F，该算法的步骤如下：

3) 令k=1到N，计算每一层所有节点的输出

输入

和期望输出

同时计算

修正权值矩阵

为介于(0，1)区间的常数.

在执行过程中，算法的步骤还涉及到“轮盘赌”的概率选择运算[9].该运算的计算过程为：计算单个个体a的目标函数值E(a)和适应度eval(a)，同时计算出个体所在群A的总适应度

然后计算每个个体被选概率

和其累计概率

在运算过程中，生成一个[0，1]内的随机数γ，如果γ<Q1，选择第1个个体；否则，选择满足Qt-1≤γ≤Qt的第t个个体.

该运算与遗传算法中的交叉运算基本一样，就是以一定的概率P将两个向量进行重新组合，令

和

表示两个运算输入参数，则其数学描述为

该算法的变异运算使用均匀变异的方法，即个体在变异时，仅随机改变个体向量中的某个分量，得到的新个体必须具有更小的目标函数值才能取代变异前的个体，如果不是，则个体保持不变，其数学表达式为

2.2　算法步骤

1) 初始化，按照上文中提到的算法来得到初步解(w，v，θ，r)，设定遗传进化代数k、输入矩阵X、目标函数值E、遗传最大代数N、交叉概率Pc和变异概率Pm.

2) 如果目标函数值E<ε(ε为常数)，跳转至步骤6)；否则，设定k=0，跳转至步骤3).

3) k=k+1，如果k≥N，跳到步骤5)；否则，计算当前解的目标函数值E.

4) 以交叉概率Pc和变异概率Pm随机对当前解进行交叉或者变异运算，得到备选解，然后使用轮盘赌选择方法对当前解和备选解进行评估和对比，生成目标函数值更小的新一代个体，跳转至步骤3).

3　仿真与分析

在网络安全评价研究领域，评价结果可以分为A(很高)、B(高)、C(一般)、D(低)4个等级，设满分为1分，这些等级的评分分布如表1[10]所示.

表1　安全等级评分分布
Tab.1　Distribution of safety level scoring

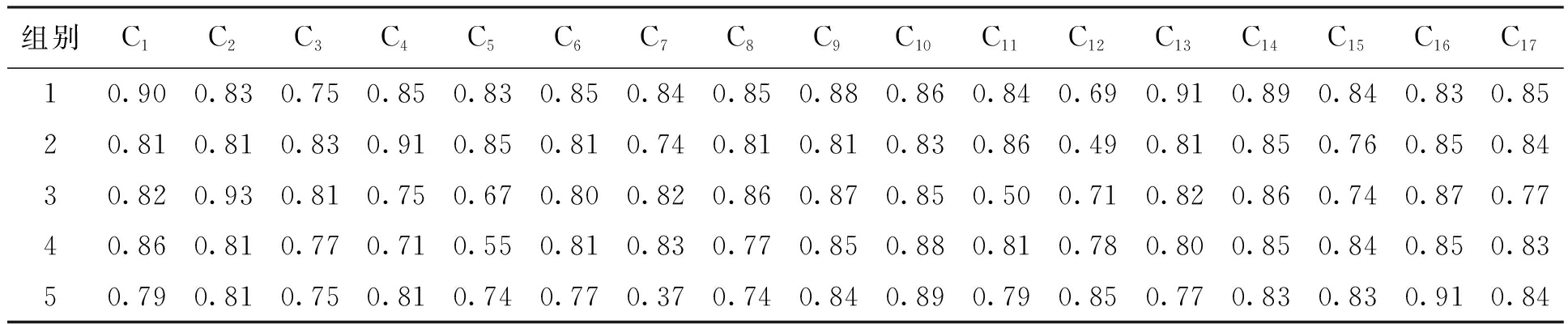
为验证GABP算法的可行性和执行效率，本文使用Matlab平台进行仿真.在具体仿真前，BP神经网络算法必须先使用多组数据进行训练，之后才能使用训练完成的神经网络进行评价.在本文中多组网络安全指标数据被用来训练神经网络.在仿真过程中，5组输入数据(每组数据C1～C17)和期望输出数据被用来进行具体的仿真评价，在执行过程中，上述算法被编译成Matlab程序脚本，首先神经网络进行了8 000多次训练，其输出误差最终达到收敛.

在神经网络算法仿真中，隐含层的节点数是一个重要参数.理论证明，如果隐含层节点数增加到一定程度，BP神经网络算法的训练误差可以无限逼近0.在仿真过程中，本文针对不同隐含层节点函数，使用GABP算法对相同数据进行训练，根据其仿真结果得到不同隐含层节点的训练误差与预测误差，分别如图3、4所示.

由图3可知，随着隐含层节点数的增加，评价算法的训练误差在不断下降，最后趋近于0，在节点数达到5之后，其下降速率就会增强，这说明隐含层节点数的增加可以增强算法的学习能力.由图4可知，随着隐含层节点数从2增加到5，评价算法的预测误差急剧降低，隐含层节点数从5增加到7时，其预测误差基本不变，隐含层节点数继续增加时，预测误差会急剧增加.这意味着隐含层节点数在比较小的时候，评价算法的预测能力会随着节点数增加而增强，然而节点数增加到一定程度时，算法中的神经网络会产生过度吻合，即节点太多反而令噪声增加，这时算法的预测能力下降.综上所述，为了令评价算法的训练误差和预测能力达到相对理想的状态，隐含层节点数最好设置在[5，7]之间.本文神经网络的隐含层节点数设置为5，学习精度设置为0.001，其仿真使用数据如表2所示.

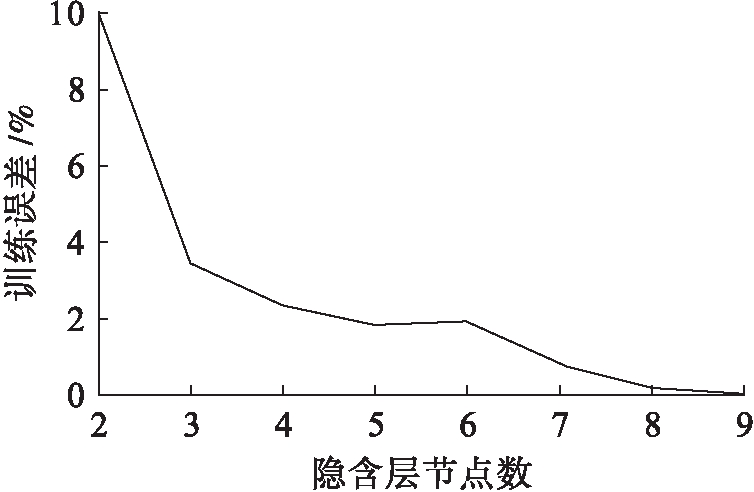
图3　不同隐含层节点数设置的训练误差
Fig.3　　　　Training error of number of nodes in different hidden layers

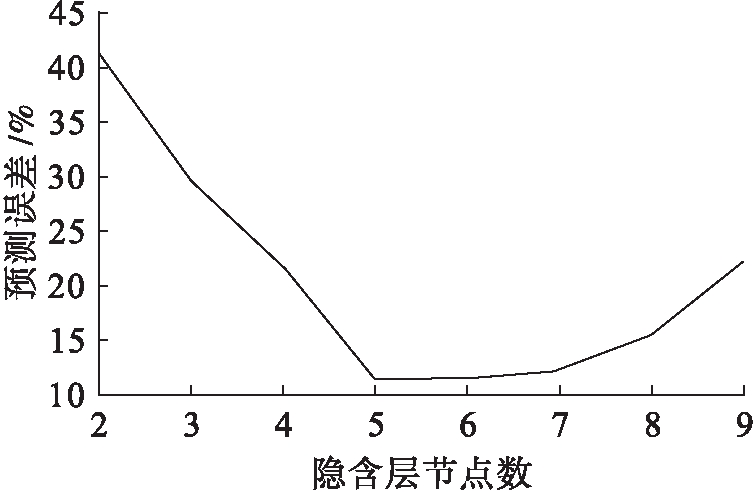
图4　不同隐含层节点数设置的预测误差
Fig.4　　　　Prediction error of number of nodes in different hidden layers

表2　仿真使用数据
Tab.2　Data used in simulation

本文网络安全仿真结果如表3所示.表3中评分是根据目标函数值E计算得出的，其计算公式为

结果表明，该模型的最大相对误差为3.7%，实际输出与期望输出基本一致，所有的网络安全等级为B，网络的安全程度较高.

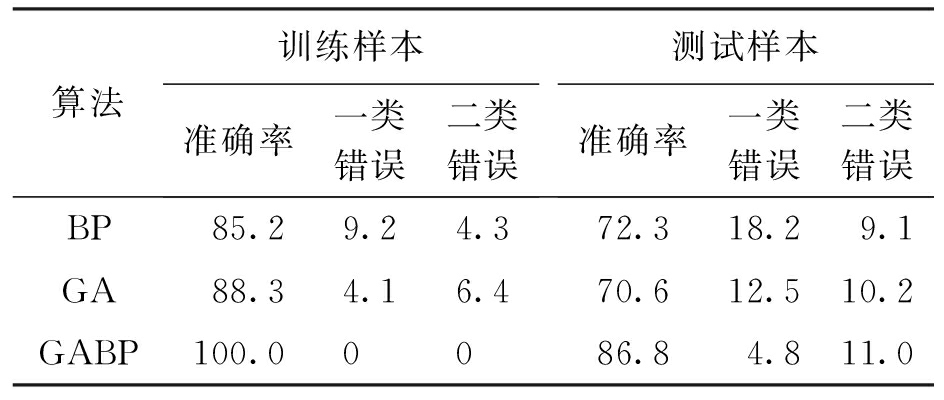
另外，将本文的算法与BP算法和遗传算法进行了误差比较，比较结果如表4所示.通过对比可以发现，本文算法的评估精度均高于BP算法和遗传算法.

表3　仿真结果
Tab.3　Simulation results

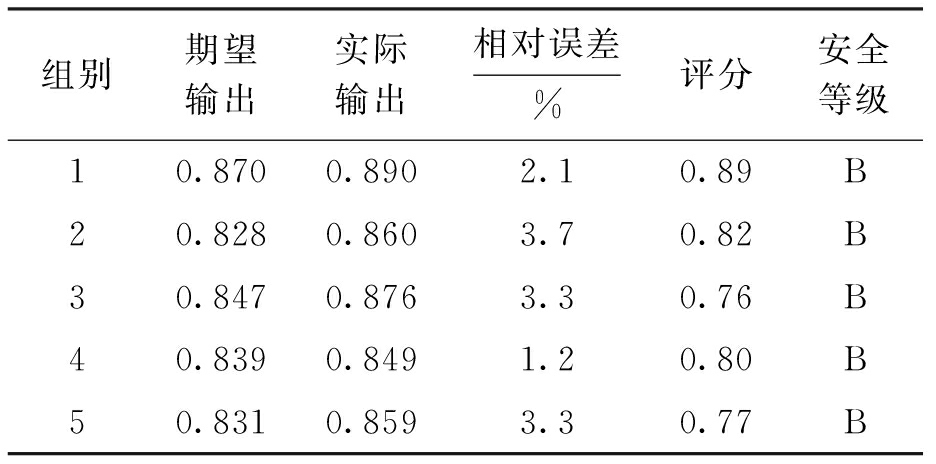
表4　BP、GA与GABP算法的误差比较
Tab.4　　　　Comparison in error of BP，GA and GABP algorithms　%

4　结　论

本文在分析神经网络算法和遗传算法的基础上，通过优化组合提出了能够评价网络信息安全的GABP算法，并对该算法的评价功能进行了逼近实际的仿真.仿真结果表明，本文所提出的GABP算法性能优于BP算法和遗传算法，可以准确地评价出网络的信息安全程度.综上所述，GABP算法可以科学评价安全指标体系，并可以使用网络实时监控数据，定量地评价出网络的信息安全状况，为未来网络信息安全研究提供了参考.

[1] 孙玉兰.基于GABP算法的计算机复杂网络可靠性评估方法研究 [J].电脑开发与应用，2014，27(12)：12-14.

(SUN Yu-lan.Research on computer complex network reliability evaluation method based on GABP algorithm [J].Computer Development and Application，2014，27(12)：12-14.)

[2] 扈诗扬，汪芳宗.基于GaBP 算法的快速潮流计算方法 [J].计算技术与自动化，2016，35(4)：76-80.

(HU Shi-yang，WANG Fang-zong.Fast GaBP algorithm power flow calculation method [J].Computing Technology and Automation，2016，35(4)：76-80.)

[3] 许卫明.基于GPU的GaBP并行算法研究 [J].湖南城市学院学报(自然科学版)，2016，25(2)：143-144.

(XU Wei-ming.Research on GaBP parallel algorithm based on GPU [J].Journal of Hunan City University (Natural Science Edition)，2016，25(2)：143-144.)

[4] 曾小燕，王林.基于优化神经网络的桁架有限元模型修正 [J].江苏科技大学学报(自然科学版)，2017，31(2)：237-240.

(ZENG Xiao-yan，WANG Lin.Modification of truss finite element model based on optimized neural network [J].Journal of Jiangsu University of Science and Technology (Natural Science Edition)，2017，31(2)：237-240.)

[5] 王华丽，王泉.访问控制列表在网络安全中的应用 [J].电子科技，2007，20(1)：58-60.

(WANG Hua-li，WANG Quan.Application of access control list in network security [J].Electronic Science and Technology，2007，20(1)：58-60.)

[6] 杨明，胡冠宇，刘倩.CMA-ES算法优化网络安全态势预测模型 [J].哈尔滨理工大学学报，2017，22(2)：140-144.

(YANG Ming，HU Guan-yu，LIU Qian.CMA-ES algorithm for optimizing network security situation prediction model [J].Journal of Harbin University of Science and Technology，2017，22(2)：140-144.)

[7] 杨云峰，唐凤仙.改进遗传算法优化神经网络的入侵检测研究 [J].河池学院学报，2017，37(2)：77-83.

(YANG Yun-feng，TANG Feng-xian.Research on improved genetic algorithm for optimizing intrusion detection of neural networks [J].Journal of Hechi Universiry，2017，37(2)：77-83.)

[8] 谢丽霞，王志华.基于CSBPNN的网络安全态势评估方法 [J].计算机应用，2017(7)：78-81.

(XIE Li-xia，WANG Zhi-hua.Network security situation assessment method based on CSBPNN [J].Computer Applications，2017(7)：78-81.)

[9] 曹成.基于GABP算法的复杂计算机网络安全评价方法 [D].合肥：合肥工业大学，2007.

(CAO Cheng.The method of the complex computer network security assement based on GABP algorithm [D].Hefei：Hefei University of Technology，2007.)

[10]高华.网络入侵失稳控制时最优节点选择 [J].沈阳工业大学学报，2017，39(1)：94-98.

(GAO Hua.Optimal node selection method under instability control after network invasion [J].Journal of Shenyang University of Technology，2017，39(1)：94-98.)

Network security evaluation model based on neural network algorithm

(Guangdong Power Grid Co. Ltd., China Southern Power Grid, Guangzhou 510630, China)

Abstract： In order to accurately evaluate the information security level of complex network, a GABP algorithm evaluation model with network security evaluation function was designed. Through introducing the Delphi method and other methods, a scientific evaluation index system was established in the proposed model. Based on the established system and through modifying some steps of BP algorithm and genetic algorithm, the appropriate objective function was selected, the algorithm flow was accurately controlled, and finally the GABP evaluation algorithm with the advantages of two algorithms was obtained. The simulation results show that the proposed algorithm can accurately evaluate the information security level of network only through entering the information security monitoring data of complex network.

Key words： neural network algorithm; genetic algorithm; Delphi method; information security; safety evaluation; Matlab software; objective function; fitness

作者简介：周　珑(1985-)，男，江西抚州人，工程师，博士生，主要从事电力信息化等方面的研究.

网络出版地址： http：∥kns.cnki.net/kcms/detail/21.1189.T.20180622.0838.012.html

基于神经网络算法的网络安全评价模型*

1 评价指标设计

1.1 评价指标种类

1.2 设计原则

1.3 评价指标体系

2 算法模型

2.1 目标函数

2.2 算法步骤

3 仿真与分析

4 结 论