基于连续非对称卷积结构的手写体数字识别<span class="superscript">*</span>

(1. 沈阳工业大学软件学院，沈阳 110870； 2. 中国科学院沈阳自动化研究所，沈阳 110016)

摘要：为了提高手写体数字识别的准确率，设计并提出了一种基于连续非对称卷积结构的手写体数字识别的深度学习算法.以连续非对称卷积结构为基础，结合极限学习机和MSRA初始化设计网络结构.在识别输入图像时，利用CUDA并行计算与Cudnn神经网络GPU加速库对手写体数字识别进行加速.在MNIST手写体数字数据库上进行实验，提出的网络结构识别准确率达到99.62%，单张图像识别速度为0.005 8 s.经实验结果对比表明，该网络结构在识别准确率和识别速度上得到有效提升.

关键词：连续非对称卷积结构；手写体数字识别；极限学习机；深度学习；批量正则化； MSRA初始化； CUDA并行计算； MNIST数据库

手写体数字识别已经应用在金融税务、邮寄分类和智能终端产品等诸多领域，目前单模型识别率已达到99.1%左右.由于各应用领域数据量急剧增大及人工智能的发展，对手写体数字的识别准确率和识别速度提出了更高的要求.作为模式识别的一个重要方法，面向手写体数字识别的神经网络得到了广泛的应用，其中常见的神经网络应用方法是20世纪提出的Lenet-5卷积神经网络结构[1]，但其识别准确率不够高，难以满足应用准确度的要求.

以Lenet-5结构为主要代表的卷积神经网络由于当时计算机性能受限，无法对算法参数和结构给出直观解释，一直以来没有受到学术和工业界的广泛关注.随着机器学习与深度学习的发展，在2012年Alex及其团队提出Alexnet，赢得2012年Imagenet冠军之后，卷积神经网络引起了广大研究人员的关注[2].近两年由于计算机硬件性能的不断提升，卷积神经网络有了突飞猛进的发展，涌现出大量优秀的研究成果.

目前许多卷积神经网络结构在大型数据库上的表现十分优异，但这些网络因为结构较为复杂(如若用在手写体数字识别问题上会出现过拟合的现象)导致识别准确率较低.同时若想训练这些复杂的网络结构需要性能极高的GPU作为硬件资源，这并不符合手写体数字识别这一问题的实际应用背景.

本文针对提高手写体数字识别准确率与识别速度这一问题，设计并构建出一种连续非对称卷积神经网络结构，并通过CUDA并行计算和Cudnn加速库对手写体数字识别进行加速.通过试验对比证明，本文方法的识别准确率和识别速度均有明显提升.

1 卷积神经网络结构设计

本文设计一种连续非对称卷积结构对输入图像进行特征提取，利用Dropout正则化在防止过拟合的同时提升网络的拟合能力，并采用极限学习机为网络增加稀疏性.

1.1 连续非对称卷积结构

卷积神经网络能够有效识别图像，主要是因为卷积层很适合针对图像进行特征提取.卷积层拥有局部感知，与人类的视觉神经感知结构更为相似.卷积层能否提取得到有效特征直接影响到卷积神经网络对图像的识别效果.所以在卷积层一般使用多神经元结构，而多神经结构会导致卷积层网络权值数量的增大，影响输入图像的识别速度.

为了在提取有效特征的同时降低网络权值的数量，本文提出了连续非对称卷积结构提取输入图像的特征，在保证网络结构提取特征能力的同时可以降低网络参数个数.连续非对称卷积结构以1×n和n×1为模块，这一组连续非对称卷积结构仅有2×n个参数，而一个n×n的卷积核需要n2个参数.

通过输入不同尺寸的图像发现，当特征图分辨率过高时不适合使用连续非对称卷积结构，信息丢失严重.当特征图分辨率过低时连续非对称卷积结构加速效果不再明显.在设计网络结构过程中得出连续非对称卷积结构适用范围的经验值：适合分辨率为10×10～30×30之间的特征图.

在手写体数字识别过程中，数字图像的分辨率较低，特征图尺寸在10×10～30×30之间，所以本文采用连续非对称卷积结构应用于手写体数字识别问题.

以数字5的某一样本作为输入图像，经由尺寸为1×3的32个卷积核神经元组成的卷积后提取得到的特征图如图1a所示，再经由尺寸为3×1的32个神经元卷积核的卷积后得到的特征图如图1b所示.图2为对输入图像直接使用由32个神经元组成的3×3卷积提取得到的特征图.

图11×3卷积与3×1卷积特征图
Fig.1Featurediagramsof1×3and3×1convolution

通过对比特征图1、2可知，使用连续非对称卷积神经网络结构提取得到的特征与直接使用传统对称卷积结构提取得到的特征图几乎一致.当特征图分辨率较高时，先使用连续非对称卷积结构提取图像特征，可以既减少权值个数，又提升网络速度，得到有效的特征图；当特征图分辨率降低后，特征图尺寸减小，通过连续非对称卷积结构减少权值个数达到加速的效果不再明显，可以直接使用传统对称卷积结构.

为了增大特征提取部分的拟合能力，本网络结构引入Dropout正则化，在防止过拟合的同时增加网络的拟合能力.Dropout正则化每次都按照设置的概率关掉该层一部分的感知器，相当于产生一个新的模型，在若干次迭代后做融合，这样便既满足了网络的拟合要求，又防止过拟合现象的发生.本网络中Dropout关闭概率通过设计网络结构过程中的经验值得出.

本网络结构在特征提取部分采用两组连续非对称卷积结构与一组传统卷积结构相结合的方式.第1组连续非对称卷积结构每层为32个神经元；第2组连续非对称卷积结构每层为64个神经元，Dropout正则化随机关闭概率为0.2；第3组为2层连续对称卷积结构，2层连续对称卷积结构每层采用128个神经元，Dropout正则化随机关闭概率为0.4.使用连续小尺寸对称卷积结构能提高网络的非线性表达能力，更好地提取局部特征[3].所有的池化层均采用最大池化的方式，网络结构参数如表1所示.

表1提取特征部分各层参数
Tab.1Parametersforeachlayerofextractedfeatureparts

1.2 极限学习机

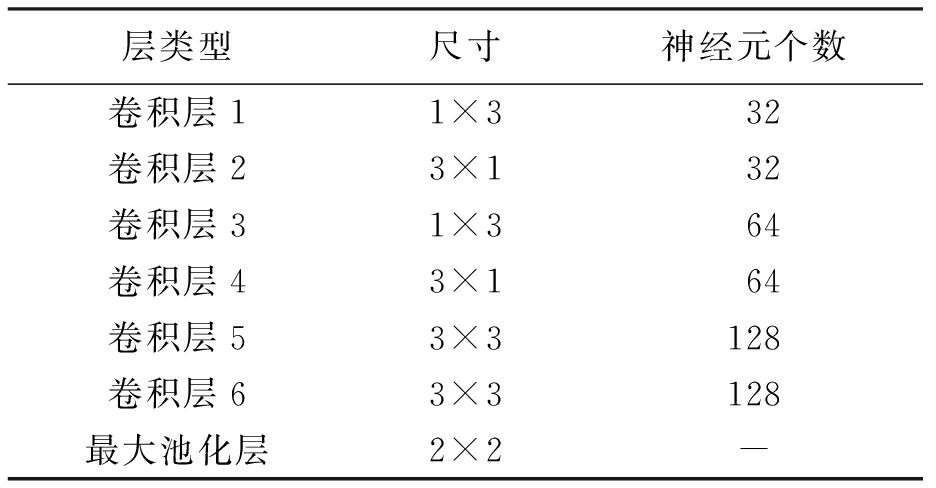
极限学习机(ELM)是由Huang等提出的一种分类器[4]，对于单隐层神经网络，极限学习机可以随机初始化权重和偏置，并得到相应的隐节点输出，极限学习机示意图如图3所示.

假设对任意样本(xj，tj)进行分类，其中xj=[xj1，xj2，…，xjn]T，tj=[tj1，tj2，…，tjn]T，若要输出的误差最小，则需

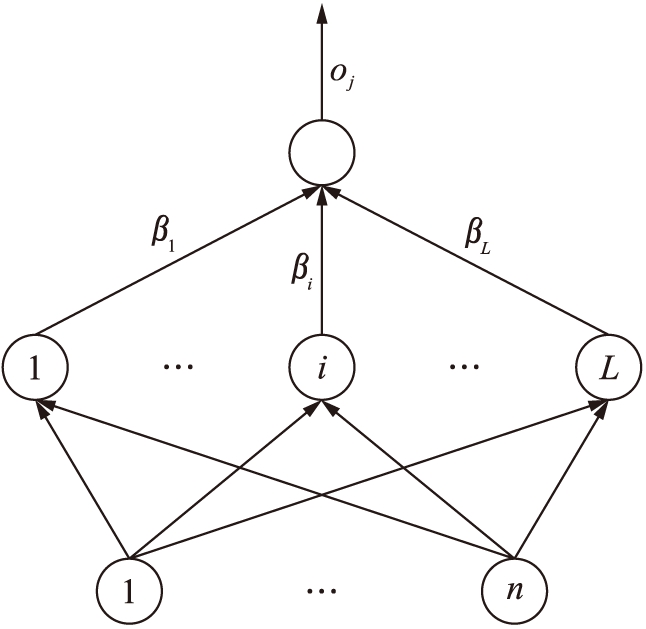
图3极限学习机网络结构
Fig.3Networkstructureofextremelearningmachine

式中：xj为输入矩阵；oj为输出矩阵；tj为期望矩阵；βi为第i个隐层单元的输出权重；g(x)为激活函数；wi为第i个隐层单元的输入权重；bi为偏置常数矩阵.

在ELM算法中，一旦输入权重wi和隐层的偏置bi被随机确定，隐层的输出矩阵h就被唯一确定，训练单隐层神经网络便可以转化为求解一个线性系统.

在提取特征图后使用ELM可以从有限的输入数据中学习到相对稀疏的特征，本网络结构利用ELM对经过特征提取得到的特征图进行分类.在经过ELM后连接两层全连接层和Relu激活函数，增大网络的拟合能力，再利用Softmax进行多分类.

2 网络训练

由于采用连续非对称卷积神经网络结构，使得网络结构深度增加，在训练过程中容易产生梯度消失和梯度爆炸的现象，所以引入了BatchNormalization正则化和MSRA初始化，防止梯度消失和梯度爆炸现象的发生[5].

2.1BatchNormalization正则化

BatchNormalization正则化通过修改网络每层的输出结果，使输出满足高斯分布，防止梯度消失和梯度爆炸的出现.

首先对输出结果根据每一维度的均值和方差进行归一化处理，即

式中：Xk为输入量；e[Xk]为输入特征期望；var[Xk]为输入特征方差；

为经过修正的输出量.

对经过修正的输出特征向量做线性变换，使输出特征向量在满足高斯分布的同时保留原有的输出信息，即

式中：yk为经过线性变换的输出；rk和αk由BP反向传播在训练过程中确定.

本网络在各卷积层和全连接层后加入BatchNormalization正则化，保证各卷积层和全连接层可以通过反向传播学习得到有效的权重.

2.2 网络初始化

本网络通过对比三种初始化方法：高斯分布的随机数初始化、哈维尔初始化和MSRA初始化后，选择MSRA初始化解决由连续非对称卷积导致网络出现梯度消失的现象.

1) 随机数初始化.由于采用连续非对称卷积结构增大网络结构深度，如果以高斯分布的随机数进行初始化将会出现梯度弥散或者梯度爆炸的现象.例如采用均值为0，方差为1的高斯分布做初始化，随着前向传播过程中隐层数目的增多，方差不断减小，最后趋近于0，将导致所有神经元输出完全相等，网络结构整体失去活力.

2) 哈维尔初始化.若采用哈维尔初始化依旧面临梯度弥散的问题，哈维尔初始化针对深层网络存在梯度消失和梯度爆炸的现象，将权重的初始化与该权重所在层的神经元个数关联起来，神经元个数应与权重始化的值成反比.但当深层网络使用Relu激活函数时，若Relu激活函数的输入小于0，将会发生截断，所以权重的方差依旧在不断衰减.

3)MSRA初始化.MSRA初始化是在哈维尔初始化的基础上，认为该层原神经元个数只有真实数目的一半，因此防止了Relu激活函数对小于0的输入产生截断.

3CUDA并行计算与Cudnn加速库

CUDA是Nvidia基于GPU推出的并行计算架构，由多个线程组成一个线程块，再由多个线程块组成一个栅格[6].使用CUDA训练网络结构过程如图4所示.

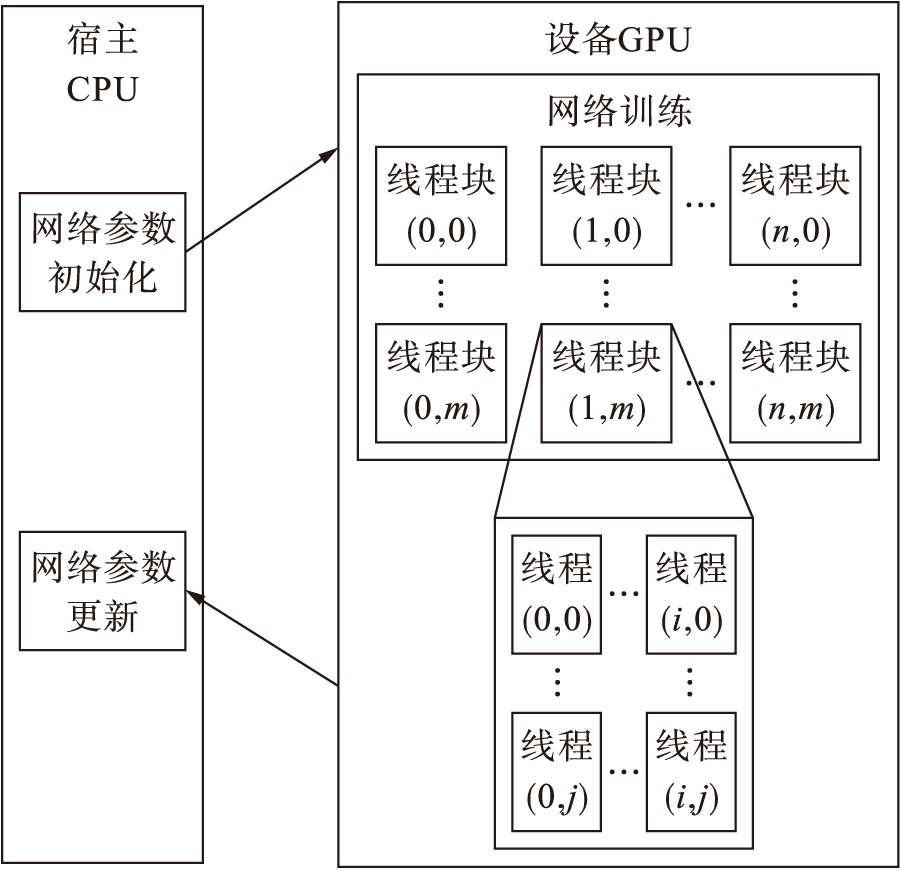
图4CUDA并行计算示意图
Fig.4SchematicdiagramofCUDAparallelcomputing

Cudnn是Nvidia针对深度神经网络设计的GPU加速库，被广泛应用于各种深度学习开源框架中.CUDA与Cudnn对卷积神经网络的加速主要体现在对卷积运算的加速.卷积神经网络主要应用在图像领域，而图像本身数据量较大，对图像进行卷积运算就需要花费大量的时间；而Cudnn能够将这些复杂的矩阵运算转化为子矩阵乘法运算，并且利用CUDA进行多线程运算，从而实现对卷积的并行加速[7].

假设当前卷积层为l，每次输入的图像为C个颜色通道，分辨率为W×H，并以M个图像样本批量随机训练，卷积层记为D∈RWHMC.设当前卷积层由K个神经元组成，卷积模板尺寸为S×Q，偏置为b，卷积层记为F∈RKCQS.卷积层输出M∈iNKPQ可表示为

式中：u，v分别为垂直与竖直方向卷积的移动步长；h，w分别为卷积补0的长度和宽度；p，a分别为卷积输出的长和宽.

由三重嵌套求和公式可知，卷积计算量极大，所以将卷积操作转换成若干子矩阵相乘.将输入D划分为若干个子矩阵Dm，将卷积模板重新组装成矩阵Fm，这样三重嵌套求和运算便转换为矩阵Fm和若干个子矩阵Dm相乘，达到了加速计算的目的[8].

通过调用Cudnn并行计算加速库，使前向传播用时明显缩短，对比在GPU下前向传播速度有明显提升.

4 实验与结果

4.1 实验环境

本文采用的硬件平台是Intel(R)Core(R)CPUI5-4570，3.2GHz，4核处理器，NVIDIA(R)GTX(R) 1050TI.软件配置为Ubuntu14.04版64位操作系统，利用了Caffe深度学习开源框架，CUDA并行计算库，Cudnn深度神经网络加速库，OpenBLAS矩阵运算加速库，Anaconda的Python计算环境发行版及opencv3.0计算机视觉库.

4.2 实验数据库

采用MNIST手写数字数据库进行训练和测试.MNIST为Google实验室和纽约大学建立的手写数字数据库，包括了0～9这10个数字，是手写体字符识别这一领域广泛使用的标准库.MNIST包含训练集6万张，测试集1万张，每张图像大小均为28×28，数据库样本图像如图5所示.

4.3 参数设计与结果分析

将本文提出的连续非对称卷积网络结构与Lenet-5网络结构在MNIST数据集中进行识别准确率与识别速度的对比实验，本文提出的网络结构参数如表2所示，实验结果如表3所示.

表3中前4项网络类型是针对本文提出的网络结构进行试验，后2项是对Lenet-5网络结构的试验结果.通过对比可以发现，相比Lenet-5，本文提出的连续非对称卷积与极限学习机结合的结构识别准确率和识别速度都有提升；相比连续对称卷积结构，达到了相同的识别准确率并且提升了识别速度.相同的网络结构在使用CUDA与Cudnn情况下，由于GPU运算精度更高，识别准确率也会有部分提升.

表2网络结构参数
Tab.2Parametersfornetworkstructure

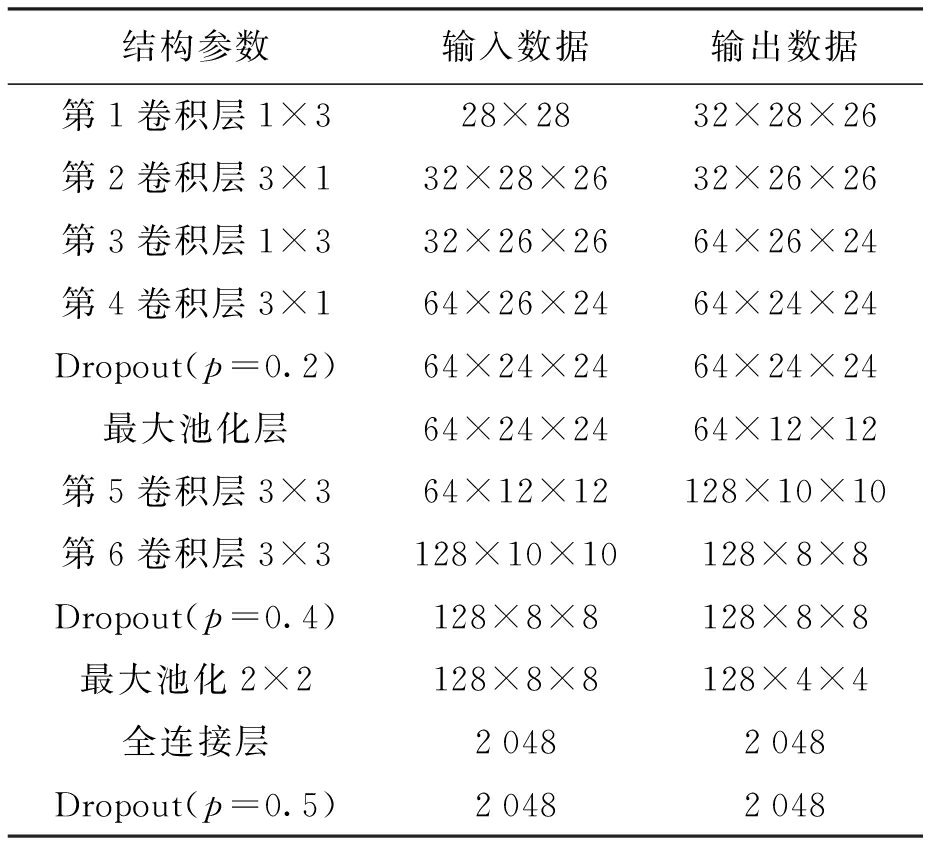
表3实验对比结果
Tab.3Experimentalcomparisonresults

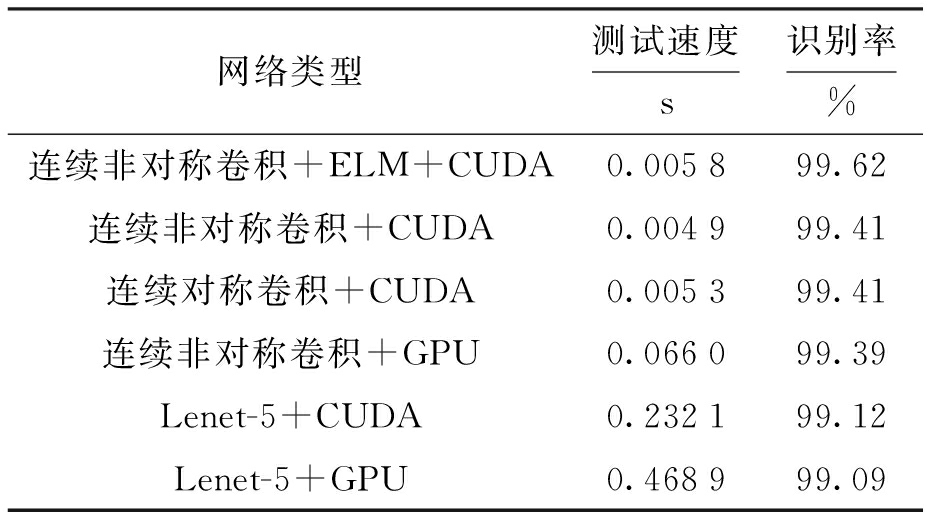
将本文提出的连续非对称卷积与极限学习机结合的结构与其它在MNIST数据库上进行测试的手写体数字识别算法进行对比，对比算法包括：基于统计和结构特征的手写体数字识别[9]、基于自适应深度置信网络的图像分类[10]及基于原型生成技术的手写体数字识别[11]，各算法识别准确率如表4所示.

表4MNIST数据库中算法比对
Tab.4AlgorithmstestedonMNISTdatabase

通过对比各算法在MNIST上测试的准确率可知，本文提出的连续非对称卷积与极限学习机结合的结构在准确率上有明显提升.

虽然本方法有较高的识别准确率，但是还有部分歧义图像仍未能正确识别，例如数字4和数字6之间的歧义如图6所示.

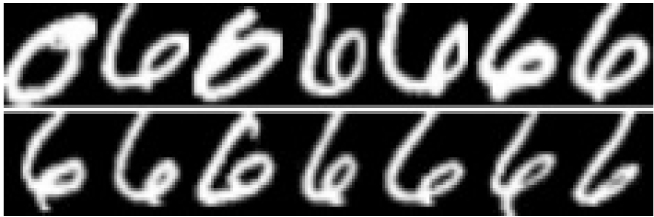
图6测试集中存在歧义的图像
Fig.6Ambiguousimagesintestingset

选取图6中图像进行测试，表5为网络结构判断输入图像中的数字分别为0～9的概率.

表5图像中的数字分别为0～9的概率
Tab.5Probabilityofnumbersfrom0to9inimage

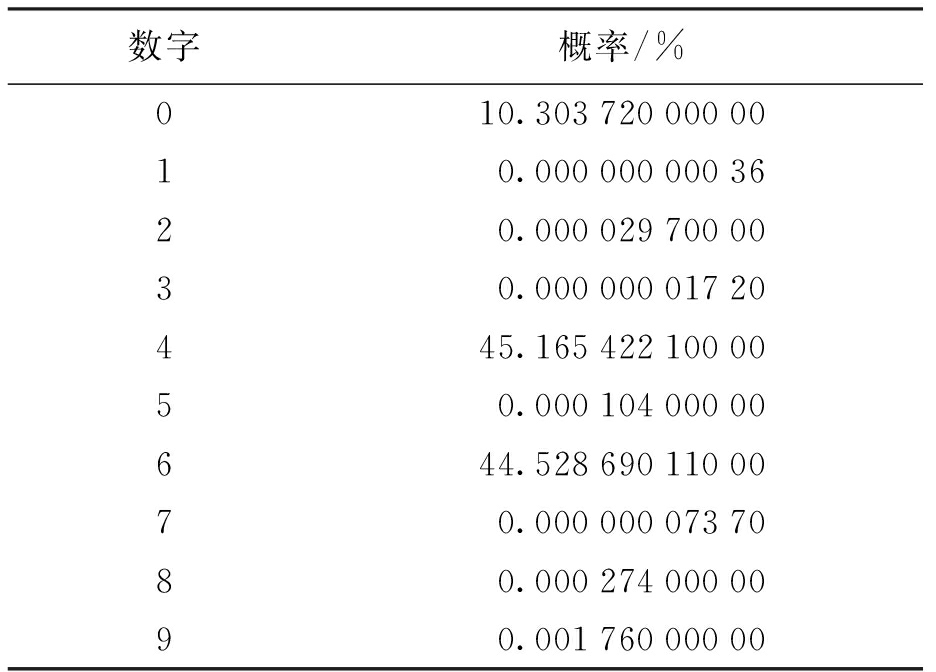
由于网络判断最大输出概率为最终识别结果，所以本网络判断出了错误结果，将图像中的数字识别为4.通过观察表5中数据概率可知，输出的9个数字中，数字0、4和6的概率都明显高于其它数字，其中数字4和6的概率最为相近，这也符合肉眼观察图像的结果.若要正确识别歧义图像，简单有效的方法是使用模型融合，利用投票原则判断歧义图像.

5 结论

本文提出了一种针对手写体数字识别的连续非对称卷积神经网络结构，并结合极限学习机、Dropout正则化和MSRA初始化提升了识别准确率.通过在MNIST数据集的测试结果表明，本结构的识别准确率达到了99.62%.未来将利用深度可分离卷积，通过剪枝与量化的方式对本网络结构进行进一步压缩与加速，使压缩后的网络结构可在嵌入式设备上运行.

[1] Alwzwazy H A，Albehadili H M，Alwan Y S，et al.Handwritten digit recognition using convolutional neural networks [J].International Journal of Innovative Research in Computer & Communication Engineering，2016，4(2)：1101-1106.

[2] 徐娟娟，陈晨，杨洪军.基于Gabor滤波器和深度学习的图像检索方法 [J].沈阳工业大学学报，2017，39(5)：529-534.

(XU Juan-juan，CHEN Chen，YANG Hong-jun.Image retrieval method based on Gabor filterand deep learning [J].Journal of Shenyang University of Technology，2017，39(5)：529-534.)

[3] 牛连强，陈向震，张胜男，等.深度连续卷积神经网络模型构建与性能分析 [J].沈阳工业大学学报，2016，38(6)：662-666.

(NIU Lian-qiang，CHEN Xiang-zhen，ZHANG Sheng-nan，et al.Model construction and performance analysis for deep consecutive convolutional neural network [J].Journal of Shenyang University of Technology，2016，38(6)：662-666.)

[4] Tang J，Deng C，Huang G B.Extreme learning machine for multilayer perceptron [J].IEEE Transa-ctions on Neural Networks & Learning Systems，2016，27(4)：809-821.

[5] Ioffe S，Szegedy C.Batch normalization： accelerating deep network training by reducing internal covariate shift [J].International Conference on Machine Learning，2015，37： 448-456.

[6] Brias A，Mathias J D，Deffuant G.Accelerating viabi-lity kernel computation with cuda architecture： applica-tion to bycatch fishery management [J].Computational Management Science，2016，13(3)：371-391.

[7] 周瑛，周尚波.面向大尺度三维重建的多核并行SIFT算法 [J].沈阳工业大学学报，2014，36(5)：555-560.

(ZHOU Ying，ZHOU Shang-bo.Multicoreparallel SIFT algorithm facing large scale three dimension reconstruction [J].Journal of Shenyang University of Technology，2014，36(5)：555-560.)

，Madzin M，Fousek J，et al.Optimizing cuda code by kernel fusion： application on blas [J].Journal of Supercomputing，2015，71(10)：3934-3957.

[9] 双小川，张克.基于统计和结构特征的手写数字识别研究 [J].计算机工程与设计，2012，33(4)：1533-1537.

(SHUANG Xiao-chuan，ZHANG Ke.Research of handwritten numeral recognition based on statistical and structure characteristics [J].Computer Engineering and Design，2012，33(4)：1533-1537.)

[10] 杨春德，张磊.基于自适应深度置信网络的图像分类方法 [J].计算机工程与设计，2015(10)：2832-2837.

(YANG Chun-de，ZHANG Lei.Image classification algorithm based on adaptive deep belief network [J].Computer Engineering and Design，2015(10)：2832-2837.)

[11] 任美丽，孟亮.基于原型生成技术的手写体数字识别 [J].计算机工程与设计，2015(8)：2211-2216.

(REN Mei-li，MENG Liang.Handwriting digit recognition based on prototype generation technique [J].Computer Engineering and Design，2015(8)：2211-2216.)

Handwrittennumeralrecognitionbasedoncontinuousasymmetricconvolutionstructure

(1. School of Software, Shenyang University of Technology, Shenyang 110870, China; 2. Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, China)

Abstract：In order to improve the accuracy of handwritten numeral recognition, a deep learning algorithm for handwritten numeral recognition based on the continuous asymmetric convolution structure was designed and proposed. Based on the continuous asymmetric convolution structure and in combination with the extreme learning machine and MSRA initialization, the network structure was designed. With identifying the input image, the CUDA parallel computing and the Cudnn neural network GPU acceleration library were used to accelerate the handwritten numeral recognition. The experiments were performed on the MNIST handwritten digital database. The accuracy of network structure recognition is 99.62%, and the single image recognition speed is 0.005 8 s. The comparison of experimental results shows that both recognition accuracy and recognition speed for the present network structure has been effectively improved.

Keywords：continuous asymmetric convolution structure; handwritten numeral recognition; extreme learning machine; deep learning; batch normalization; MSRA initialization; CUDA parallel computing; MNIST database

* 本文已于2018-08-30 15∶18在中国知网优先数字出版. 网络出版地址： http：∥kns.cnki.net/kcms/detail/21.1189.T.20180829.1555.005.html

作者简介：张志佳(1974-)，男，河北晋州人，教授，博士生导师，主要从事机器视觉检测技术、图像处理与模式识别等方面的研究.

基金项目：国家自然科学基金资助项目(61540069)；装发部共用技术课题项目资助(Y6k4250401).

基于连续非对称卷积结构的手写体数字识别*