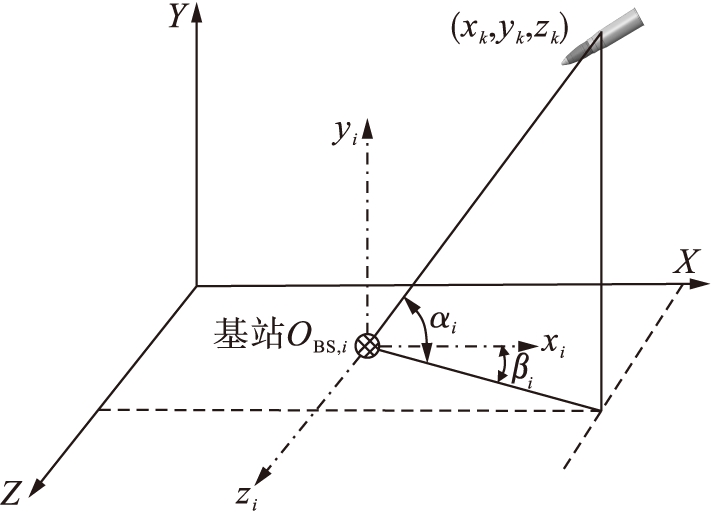
图1定位系统模型
Fig.1Modelforlocationsystem
吴清怡, 吴中红
(海军工程大学 电子工程学院, 武汉 430033)
摘要:针对全球定位系统、雷达和卡尔曼滤波等传统测量手段在弹道量测中面临的诸多问题,提出了超宽带技术与平方根无迹卡尔曼滤波方法相结合的弹道估计算法,通过试验与仿真对该算法进行了分析.结果表明,采用平方根无迹卡尔曼滤波进行估计时,运行时间低于扩展卡尔曼滤波,略高于无迹卡尔曼滤波,且位置和速度均方根误差均低于二者.将平方根无迹卡尔曼滤波应用于弹道估计问题中可取得更为有效、准确的估计结果.
关键词:超宽带; 弹道估计; 平方根无迹卡尔曼扩展滤波; 扩展卡尔曼滤波; 无迹卡尔曼滤波; 运行时间; 位置均方根误差; 速度均方根误差
准确、实时的弹道估计可大幅度提高炮弹观测与校正的精确度,优化武器系统的作战效能.在实际弹丸定位过程中,常采用传感器[1-2]、全球定位系统[3-4]和雷达[5]等无线定位手段,以实现弹道的估计.但这些定位技术仍存在易受大气和噪声等环境因素影响,抗干扰性弱,测量实时性较低,不能对记录目标进行准确标记等问题.因此,本文采用超宽带(ultra-wide band,UWB)技术,利用该技术不易受环境因素影响、抗干扰性强、启动时间短、体积小、易安装和多条数据同时记录等优点,可有效解决上述问题.
文献[6-12]对几种弹道估计的滤波方法进行了分析对比.文献[6]提出了一种基于空域追踪的修正算法,通过非线性滤波器从原始信号中粗提出基线信号,利用多步迭代微分算子消除噪声误差;文献[7-8]采用扩展卡尔曼滤波(EKF)降低目标定位误差;文献[9-10]使用无迹卡尔曼滤波(UKF),通过提高滤波的收敛速度来实现优化估计精度的目的;文献[11]提出了引入积分预测算法来减少离散卡尔曼滤波器一步预测的误差;文献[12]采用方差补偿方法建立自适应卡尔曼滤波算法完成目标跟踪.其中,EKF由非线性方程进行泰勒展开保留一次项得到,由于其忽略了高次项使得精度降低,且EKF对初始值较敏感,设置不当易造成滤波发散,需要计算雅克比矩阵,复杂度较高;UKF是一种求采样点的非线性滤波方法,计算精度可达到二阶或三阶的泰勒展开精度,性能优于EKF,但当非线性系统维度大于3时,该方法很有可能受到非正定协方差的影响,造成滤波发散,使估计精度大大降低.
为了避免出现非正定协方差,本文采用平方根无迹卡尔曼滤波(square root unscented Kalman filter,SRUKF)进行弹道估计,仿真结果表明,EKF具有较低的复杂度,但估计精度明显低于SRUKF和UKF,且SRUKF与UKF相比具有较强的稳定性.综上所述,在针对六维弹道估计问题上,EKF、UKF、SRUKF三种滤波方式中,SRUKF具有最优越的综合性能.
本文以质点弹道方程为依据建立模型,坐标系中Y轴与地面相垂直,弹丸质点坐标为(xk,yk,zk);各定位基站坐标分别为(x1,y1,z1),(x2,y2,z2),…,(xk,yk,zk),定位基站i相对于弹丸目标的俯仰角为αi,方位角为βi,定位系统模型如图1所示.

图1定位系统模型
Fig.1Modelforlocationsystem
为了简化定位算法的复杂度,以质点弹道方程为依据建立系统状态方程,现假设弹丸为一质点,该质点的位置坐标与各方向上的速度表示为[x,y,z,Vx,Vy,Vz]T,则质点弹道方程组[13]可表示为
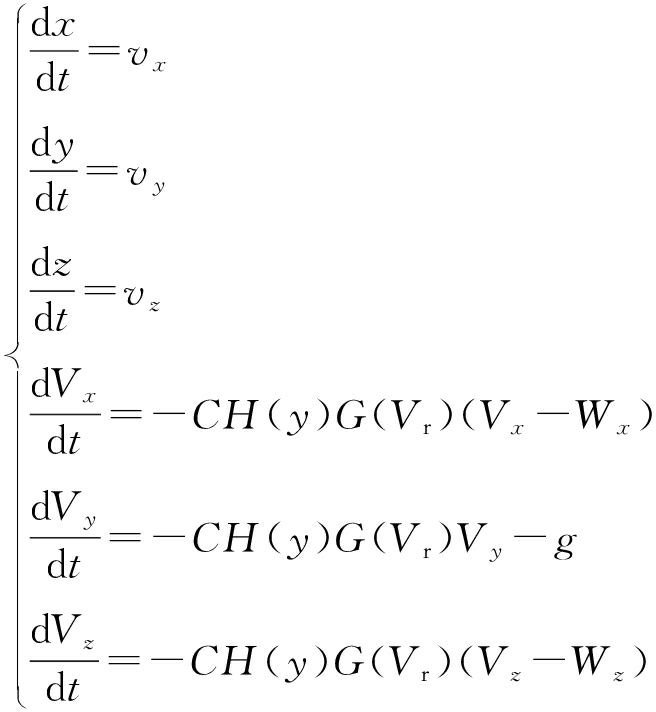
(1)
式中:C为弹道系数;H(y)为空气密度函数;G(Vr)为空气阻力函数;![]() 为目标相对速度;Wx为纵风速度;Wz为横风速度;g为重力加速度.
为目标相对速度;Wx为纵风速度;Wz为横风速度;g为重力加速度.
当y≤10 000 m时,空气密度函数依据经验公式[13]可表示为
(2)
空气阻力函数表达式[13]为
(3)
式中:ρON=1.206 kg/m3为地表空气密度标准值;S为沿速度方向弹丸投影面积;CXON为标准阻力系数;![]() 其中,V为弹丸质心速度,k为绝热指数,R为气体常数,τ为虚温.则式(3)可表示为
其中,V为弹丸质心速度,k为绝热指数,R为气体常数,τ为虚温.则式(3)可表示为
G(Vx)=4.737×10-4VCXONVx/Cs
(4)
综上所述,选取弹丸位置、速度(x,y,z,Vx,Vy,Vz)为状态变量,设X=[x1,x2,x3,x4,x5,x6]T,则离散状态方程可表示为
Xk+1= f(Xk)+wk=
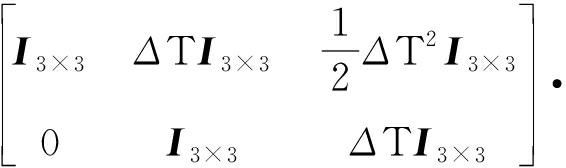
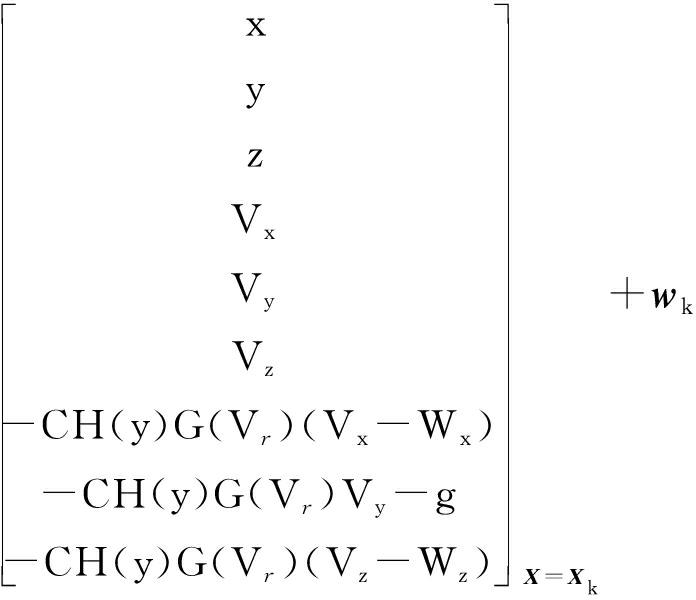
(5)
式中:f()为状态转移函数;ΔT为抽样时间间隔;wk为过程噪声,其均值为零,协方差为Qk.该方程在计算过程中必然会存在受各种因素影响所产生的误差,因此需要对误差进行补偿处理.
系统采用测量到达时间差与到达角度的方法建立系统测量方程.将1号定位基站设为参考基站,系统需要测量相对于参考基站各基站接收目标信号所需要的时间差Δti1,以及各个基站接收目标信号的俯仰角αi与方位角βi.
1.2.1 基于到达时间差的测量方程
基于到达时间差测量方程的表达式为
(6)
(7)
(8)
式中:ri为定位基站i与目标弹丸的距离;ti为第i个基站接收目标信号所需时间;t1为第1个基站接收目标信号所需时间;r1为第1个基站与目标的距离;c为电波传播速度.由式(6)~(8)可得基于TDOA算法的测量方程,即
vk-TDOA
(9)
式中,vk-TDOA为测量到达时间差的测量噪声.
1.2.2 基于角度的测量方程
设第i个基站测得目标俯仰角为αi,方位角为βi,则有
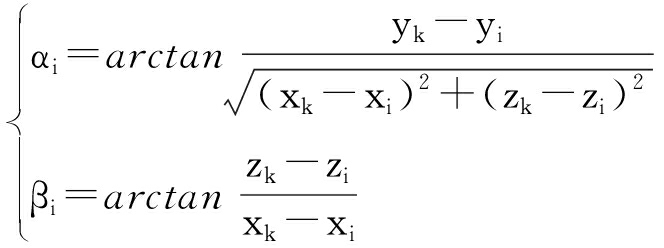
(10)
由式(10)可得,基于AOA方法的测量方程为
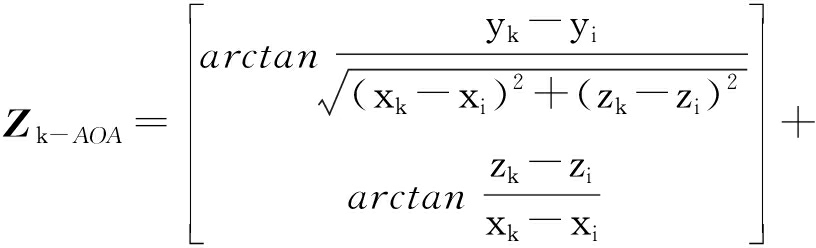
vk-AOA
(11)
式中,vk-AOA为测量角度时的测量噪声.
1.2.3 到达时间差与角度联合的测量方程
基于到达时间差与角度联合的测量方程所需测量值为z=[ri1,α,β]T,则测量方程为
(12)
式中:h()为测量转移函数;vk=[vk-TDOA,vk-AOA]T,vk-TDOA满足![]() 的分布特性,vk-AOA满足
的分布特性,vk-AOA满足![]() 的分布特性,二者相互独立,且与Xk和wk不相关,则vk的协方差为
的分布特性,二者相互独立,且与Xk和wk不相关,则vk的协方差为![]()
无迹卡尔曼滤波算法(UKF)通过选取一组采样点(sigma点)来计算系统的协方差,有效提高了估计精度,降低了算法复杂度,在解决非线性问题中具有广泛的应用[14].但是,该方法在使用过程中可能会出现非正定协方差,导致滤波不稳定甚至发散.为了解决这一问题,Steven等[15]于2008年提出平方根无迹卡尔曼滤波.SRUKF建立在UKF的基础上,直接利用协方差矩阵的平方根参与递推运算,避免了协方差的非正定性,能有效提高滤波稳定性.
使用SRUKF算法,首先需要建立非线性的状态方程与测量方程[16],即
(13)
具体步骤如下:
1) 初始化,其表达式为
(14)
(15)
式中,Xa为扩充状态向量,Xa=[XT,WT,VT],XT为状态变量,WT为系统噪声,VT为观测噪声.
2) 选取权值,即
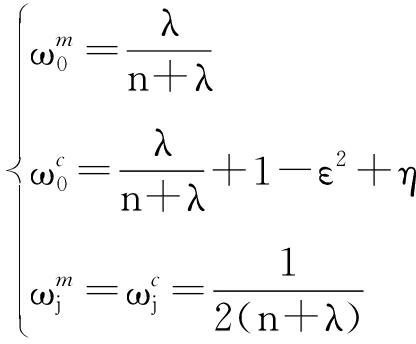
(16)
式中:λ=ε2(n+κ)-n为尺度调节因子,n为状态变量维数,10-4≤ε≤1,κ为次尺度调节因子,通常取0;j为第j个sigma点,j=1,2,…,2n;η用来体现X的分布,对于高斯分布![]() 表示均值(mean)的权值,
表示均值(mean)的权值,![]() 表示协方差(covariance)的权值.
表示协方差(covariance)的权值.
3) 取sigma点,即
(17)
式中,![]()
4) 预测误差协方差,其表达式为
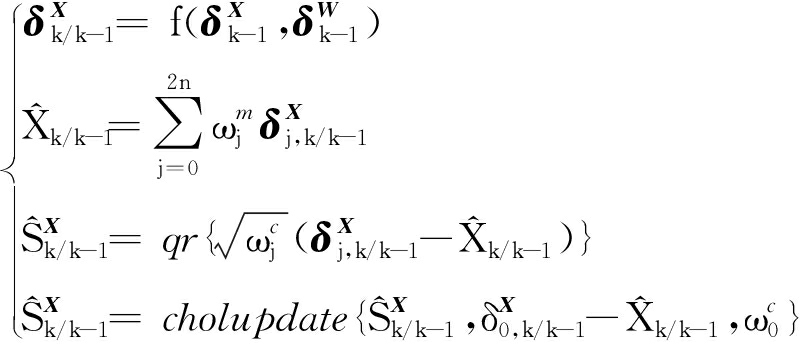
(18)
式中:qr表示QR分解;cholupdate表示choleskey一级更新.
5) 预测互协方差平方根,计算一步预测、方差以及互协方差平方根,其表达式为
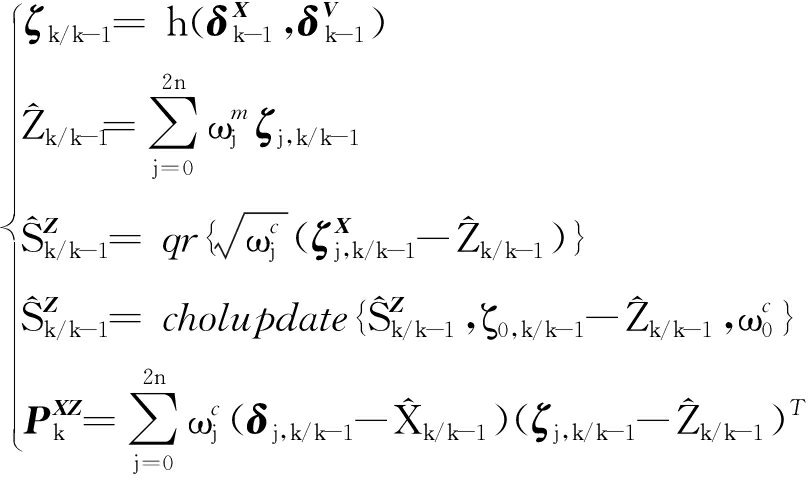
(19)
6) 计算状态误差方差平方根,即
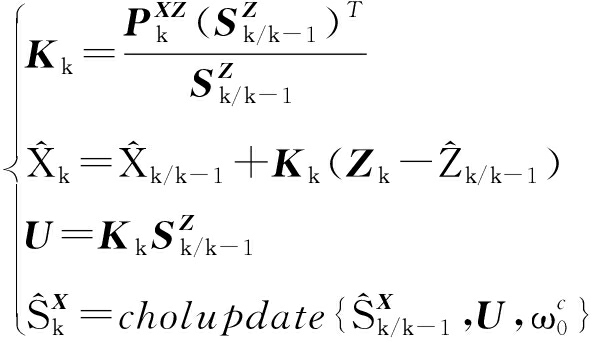
(20)
结合式(14)~(20),通过UWB设备中定位基站测得的炮弹坐标为系统提供采样点,则可实现基于平方根无迹卡尔曼滤波算法的弹道估计.
在实弹试验中设置坐标系,将发射起点布设在X0=[20 000,0,80,-879,190,-12]T坐标点上,定位基站分别布设在坐标原点、(50,0,0)、(-50,0,0)三个坐标点上,发射后,通过高清摄像和UWB设备可得两组轨迹,如图2所示.由高清摄像所得轨迹为炮弹实际运动轨迹,通过UWB设备所得轨迹为炮弹测量轨迹.由图2可知,UWB测量轨迹相对误差较大,需对其测量结果作进一步校正.在上述试验的基础上,使用EKF、UKF、SRUKF三种滤波算法对UWB测量轨迹进行仿真处理,并分析仿真结果.首先设状态变量X=[x,y,z,Vx,Vy,Vz]T的初始值为X0=[20 000,0,80,-879,190,-12]T;测量TDOA的定位基站坐标分别为BS1(50,0,0)、BS2(-50,0,0);测量方位角与俯仰角角度的定位基站坐标为BS3(0,0,0);ΔT为0.25s;纵风Wx为10m/s;横风Wz为10m/s;过程噪声方差q=1;距离测量噪声标准差σr=50m;角度测量噪声标准差σα=σβ=0.5°.
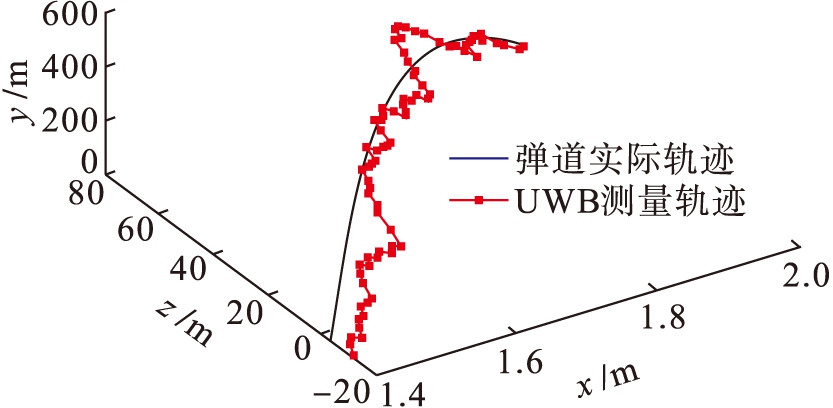
图2弹道运动轨迹与测量轨迹
Fig.2Motionandmeasurementtrajectories
现以均方根误差(root mean square error,RMSE)为评判依据,对EKF、UKF、SRUKF三种滤波的性能进行仿真与分析,即
(21)
式中:Q为仿真次数;xl(t)和![]() 分别为第l次仿真得到的状态向量在t时刻的真值和估计值.
分别为第l次仿真得到的状态向量在t时刻的真值和估计值.
根据设置初始条件和参数,进行300次Monte-Carlo仿真,其中,UKF算法在运行过程中由于出现非正定协方差矩阵将仿真次数缩减为200次,EKF、UKF、SRUKF三种滤波算法所得目标位置与速度的误差对比曲线如图3、4所示,误差均值对比如表1所示,200次Monte-Carlo仿真运行时间对比如表2所示.
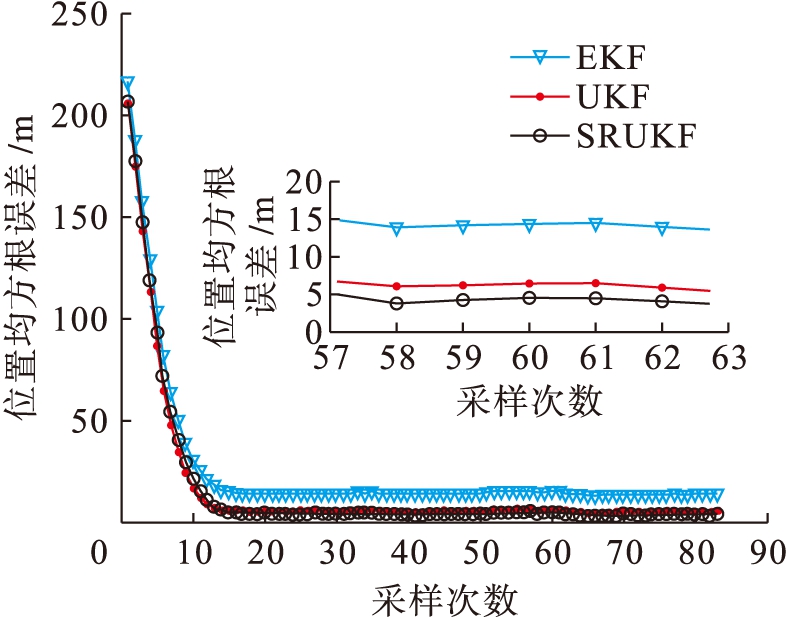
图3三种滤波方式的位置均方根误差
Fig.3RMSEofpositionforthreefilteringways
由图3、4可以看出,在三种滤波方式中,SRUKF估计精度最高,UKF略低,EKF估计精度明显低于前两者.由表1可以看出,SRUKF较EKF和UKF的位置估计精度分别提高了42.11%和9.84%,速度估计精度分别提高了31.13%和7.98%.由表2可以看出,UKF与SRUKF所需时间分别是EKF的2.8和2.4倍,由此可知,EKF复杂度明显低于UKF和SRUKF,SRUKF由于直接使用协方差的平方根进行递推和计算,其复杂度略低于UKF,运行时间是UKF的86%.
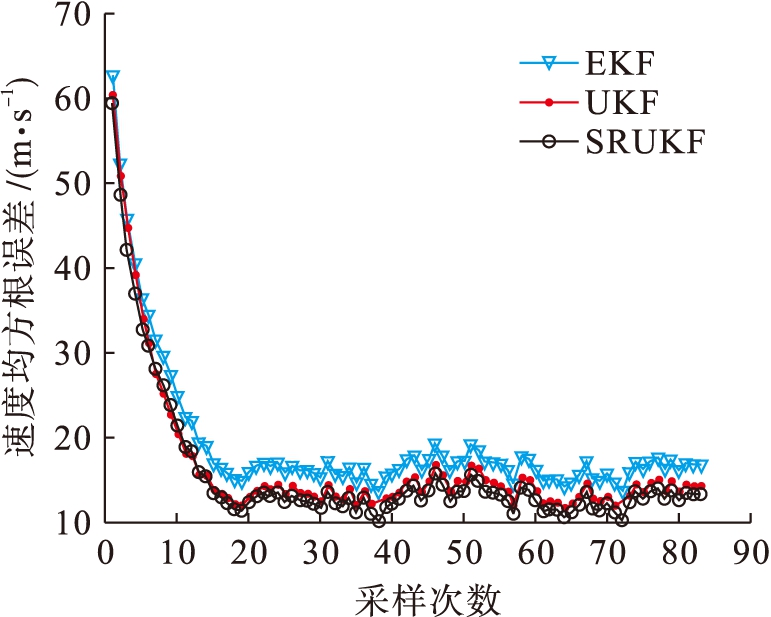
图4三种滤波方式的速度均方根误差
Fig.4RMSEofspeedforthreefilteringways表1各算法精度对比
Tab.1Comparisoninaccuracyofeachalgorithm
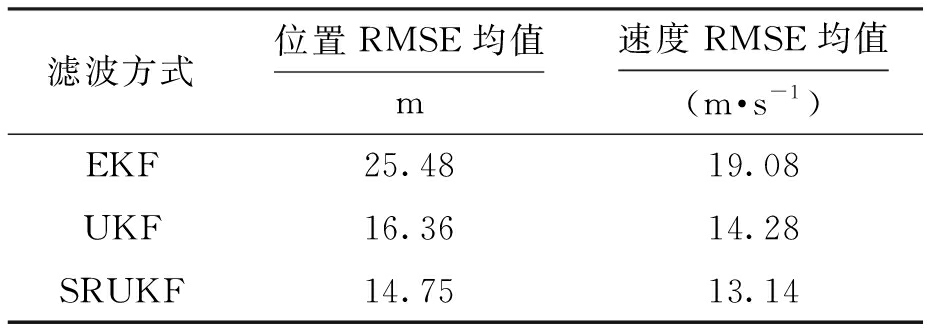
表2三种滤波方式运行时间
Tab.2Runningtimeofthreefilteringways

通过仿真试验表明,采用SRUKF进行滤波估计能较好地克服UKF的协方差非正定和复杂度较高等问题,且估计精度较EKF与UKF相比均有所提高,保证了弹道估计的高效性、稳定性及精确度.但在试验过程中发现,该方法在使用的过程中,基站的布设以及噪声的不确定性对定位精度仍具有较大的影响,需要做出进一步的研究和改进.
参考文献(References):
[1] 张慧.天基红外传感器对中段目标群跟踪技术研究 [D].长沙:国防科学技术大学,2014.
(ZHANG Hui.Tracking techniques for midcurse target complex via space-based infrared sensors [D].Changsha: National University of Defense Technology,2014.)
[2] 陈延军,潘泉,王征.无线传感器网络目标跟踪性能优化及仿真 [J].传感技术学报,2015,28(4):544-550.
(CHEN Yan-jun,PAN Quan,WANG Zheng.Performance optimization and simulation based on target tracking in wireless sensor networks [J].Chinese Journal of Sensors and Actuators,2015,28(4):544-550.)
[3] 张丽艳,杜忠华,张志安,等.基于GPS的弹道修正弹驱动控制器系统 [J].火力与指挥控制,2015,40(2):144-147.
(ZHANG Li-yan,DU Zhong-hua,ZHANG Zhi-an,et al.Study of trajectory correction drive controller based on GPS [J].Fire Control & Command Control,2015,40(2):144-147.)
[4] 张超,顾济华.基于GPS/BDS的移动目标定位追踪系统设计 [J].现代电子技术,2015,38(17):121-123.
(ZHANG Chao,GU Ji-hua.Design of mobile target tracking system based on GPS/BDS [J].Modern Electronics Technique,2015,38(17):121-123.)
[5] 冯存前,李靖卿,贺思三,等.组网雷达中弹道目标微动特征提取与识别综述 [J].雷达学报,2015,4(6):609-620.
(FENG Cun-qian,LI Jing-qing,HE Si-san,et al.Micro-doppler feature extraction and recognition based on netted radar for ballistic targets [J].Journal of Radars,2015,4(6):609-620.)
[6] 谢芳娟,朱淑云.基于空域追踪算法的基线漂移信号噪声修正 [J].沈阳工业大学学报,2016,38(6):692-696.
(XIE Fang-juan,ZHU Shu-yun.Baseline drift noise correction based on null space pursuit algorithm [J].Journal of Shenyang University of Technology,2016,38(6):692-696.)
[7] 王佳伟,史凯,徐国泰.基于扩展卡尔曼滤波的高转速修正引信滚转角测量方法 [J].西北工业大学学报,2016,34(6):938-944.
(WANG Jia-wei,SHI Kai,XU Guo-tai.Roll estimation of high rotation speed correction fuze based on extended Kalman filter [J].Journal of Northwestern Polytechnical University,2016,34(6):938-944.)
[8] 吴汉洲,宋卫东,徐敬青.基于多项式拟合的扩展卡尔曼滤波算法 [J].计算机应用,2016,36(5):1455-1457.
(WU Han-zhou,SONG Wei-dong,XU Jing-qing.Ex-tended Kalman filtering algorithm based on polynomial fitting [J].Journal of Computer Applications,2016,36(5):1455-1457.)
[9] 黄佳,崔乃刚.基于UKF的导弹飞行试验弹道重构方法研究 [J].弹箭与制导学报,2015,35(1):95-99.
(HUANG Jia,CUI Nai-gang.Research on trajectory reconstruction of missile flight test based on UKF [J].Journal of Projectiles,Rockets,Missiles and Guidance,2015,35(1):95-99.)
[10] 潘建平,王盛玺,刘宗伟.集群系统下多弹道实时测量数据处理的UKF算法 [J].电子设计工程,2016,24(13):61-63.
(PAN Jian-ping,WANG Sheng-xi,LIU Zong-wei.UKF algorithm for real-time measurement of multi trajectory data processing in cluster system [J].Electronic Design Engineering,2016,24(13):61-63.)
[11] 杨荣军,王良明,修观.卡尔曼滤波在弹道重构中的应用与仿真 [J].火力与指挥控制,2011,36(11):156-158.
(YANG Rong-jun,WANG Liang-ming,XIU Guan.Simulation and application of Kalman filter in trajectory reconstruction [J].Fire Control & Command Control,2011,36(11):156-158.)
[12] 许哲明.基于卡尔曼滤波的地表移动变形预测 [J].沈阳工业大学学报,2017,39(5):557-561.
(XU Zhe-ming.Prediction of surface movement deformation based on Kalman filtering [J].Journal of Shenyang University of Technology,2017,39(5):557-561.)
[13] 高强,王力,侯远龙.火控系统设计概论 [M].北京:国防工业出版社,2016:40-43.
(GAO Qiang,WANG Li,HOU Yuan-long.Introduction to fire control system design [M].Beijing:National Defend Industry Press,2016:40-43.)
[14] Kolas S,Foss B A,Schei T S.Constrained nonlinear state estimation based on the UKF approach [J].IEEE Transactions on Automatic Control,2009,33(8):1386-1401.
[15] Steven H,Georg K,David W M.A square root unscented Kalman filter for visual on SLAM [C]//2008 IEEE International Conference on Robotics and Automation.Pasadena CA,USA,2008:3710-3716.
[16] 耿文东,王元钦.群目标跟踪 [M].北京:国防工业出版社,2014:20-26.
(GENG Wen-dong,WANG Yuan-qin.Group-targets tracking [M].Beijing:National Defend Industry Press,2014:20-26.)
WU Qing-yi, WU Zhong-hong
(College of Electronic Engineering, Naval University of Engineering, Wuhan 430033, China)
Abstract:In order to solve many problems in the traditional measurement methods such as the global positioning system (GPS), radar and Kalman filtering, the trajectory estimation algorithm in combination with both ultra wide band (UWB) technology and square root unsented Kalman filtering (SRUKF) was proposed. In addition, the proposed algorithm was analyzed through the simulation and experimets. The results show that the running time of SRUKF is lower than that of extended Kalman filtering (EKF), while higher than that of unsented Kalman filtering (UKF). However, the root mean square error (RMSE) of both position and speed of SRUKF is lower than those of EKF and UKF. When the SRUKF is used for the trajectory estimation problem, the more effective and accurate estimating results can be obtained.
Keywords:ultra wide band; trajectory estimation; square root unsented Kalman filtering; extended Kalman filtering; unsented Kalman filtering; running time; root mean square error of position; root mean square error of speed
doi:10.7688/j.issn.1000-1646.2018.05.16
* 本文已于2018-06-07 13∶06在中国知网优先数字出版. 网络出版地址: http:∥kns.cnki.net/kcms/detail/21.1189.T.20180606.1129.004.html
作者简介:吴清怡(1985-),女,辽宁锦州人,讲师,博士,主要从事无线定位等方面的研究.
基金项目:总装备部装备预研基金资助项目(9140A06030215JB11082).
收稿日期:2018-03-04.
文章编号:1000-1646(2018)05-0571-06
文献标志码:A
中图分类号:TN 014
(责任编辑:钟 媛 英文审校:尹淑英)