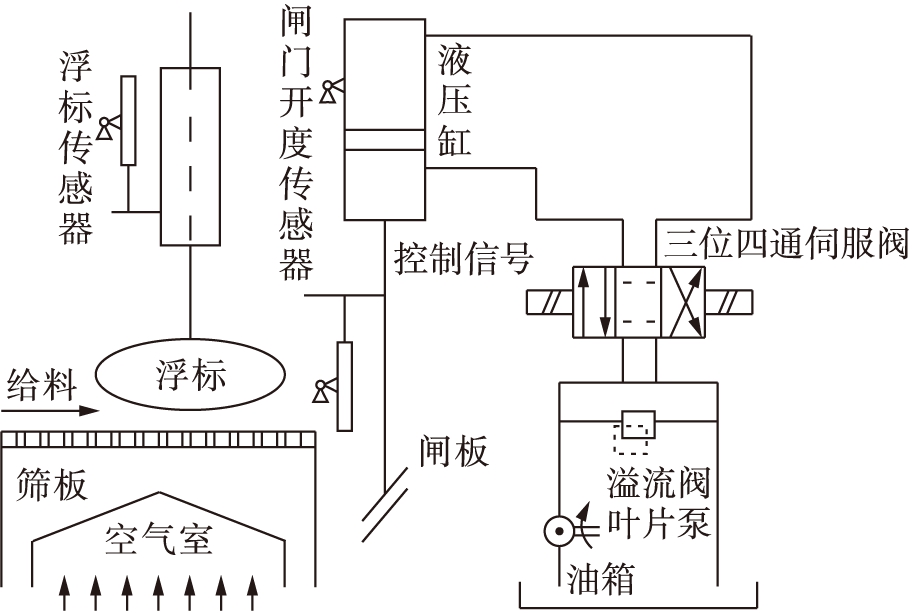
图1跳汰机排料系统原理图
Fig.1Principlediagramofdischargesystemofjigger
马玥珺, 张湘玉
(河北工程大学 机械与装备工程学院, 河北 邯郸 056038)
摘要:针对传统PID控制在复杂跳汰机排料系统中控制精度不高、响应速度慢、参数调整不够精确等问题,提出了一种基于QPSO算法优化的分数阶PIλDμ控制器(QPSO-FOPID).该控制器利用分数阶微积分理论,将传统PID控制由整数阶次推广到复数阶次,并增加了两个参数的自由度.同时利用量子粒子群算法对分数阶PIλDμ控制器参数进行寻优,解决参数调整不精确的问题.以某矿井跳汰机排料系统为例,建立跳汰机排料系统控制的Simulink仿真模型.仿真结果表明,该方法不仅能够实现分数阶PIλDμ控制参数的在线优化,收敛速度快,具有较强的鲁棒性,还具有良好的动、静态性能,无超调现象,控制精度高.
关键词:跳汰机; 排料系统; 分数阶微积分理论; 量子粒子群算法; PID控制器; 分数阶PIλDμ控制器; 在线优化
跳汰机是煤炭分选的关键设备之一,其主要作用是利用矿料间密度和比重的差异进行产品的分选,同时将床层厚度维持在一个稳定、合适的位置,使跳汰机具有良好的分选状态,从而保证精煤质量[1].因此,精确控制跳汰机自动排料系统对整个矿厂的运营至关重要.跳汰机排料系统的运行过程,决定了整个系统是一个典型的大滞后、非线性、随机干扰多等的复杂系统,很难用精确的模型来描述.对跳汰机排料系统的控制,目前主要采用常规PID控制、模糊神经网络控制、遗传算法优化PID控制和模糊预测控制等.其中,由于PID自身的一些局限性,例如参数整定和对模型的依赖等问题,使得控制性能不太理想,但是原理简单,使用方便,结构简单[2];神经网络算法需要大样本训练,且容易出现数值病态和陷入局部最优问题,控制效果有时难以达到理想值;遗传算法对新空间探索能力较差,容易早熟陷入局部最优且优化维度较低,计算量较大.
为此,研究人员在分数阶理论研究的基础上,提出了分数阶PIλDμ控制器,它比传统PID控制器多了积分阶次λ和微分阶次μ,增加了控制器的灵活度,实现PID由点到面的控制.相比于传统PID控制,分数阶PIλDμ控制器继承了传统PID控制的优点并具有更灵活的结构和更强的鲁棒性,其控制律的变化也更加精确,能够获得更优的动态性能和鲁棒性能.在此基础上,本文将量子粒子群算法(QPSO)与分数阶PIλDμ相结合,其中,QPSO算法模型是从量子力学角度出发提出的一种新的PSO算法,改变了传统PSO算法的收敛方式,即轨道形式和粒子速度的限制,在QPSO算法中,其运动状态可以用波动函数ψ(x,t)来描述.通过量子粒子群算法来优化分数阶PIλDμ的参数,使得分数阶参数达到最优,从而能够获得期望的优越控制品质,能更好地稳定跳汰机室内床层厚度,保证选煤的质量.
跳汰机排料系统原理图如图1所示.该系统由筛板、空气室、浮标、浮标传感器和闸板等构成.对于跳汰机排料系统,其筛板上床层的厚度对整个系统的良好运行和分拣效果起到至关重要的作用.因此,该控制系统的控制目标是通过控制阀门开度的大小,来稳定床层给料的厚度,其控制原理为当系统给料在经过上方的浮标时,浮标传感器将给定系统实际厚度的信号与系统设定的厚度在比较器中形成厚度误差信号,送给控制器(如传统的PID控制).根据控制器算法的计算发出控制信号到执行机构(闸门),通过控制阀门开度的大小来改变床层的厚度.若厚度太大,闸门开度增加,反之将减小闸门开度,从而使床层厚度稳定在设定值上.同时,系统要控制好排料的速度,排料速度太快或太慢都会给分拣系统造成不良结果.太快将会造成床层厚度太薄,太慢又会造成床层厚度太厚.为了解决上述问题,本文提出了采用QPSO算法优化的分数阶PIλDμ控制器来实现排料的方法[3].

图1跳汰机排料系统原理图
Fig.1Principlediagramofdischargesystemofjigger
2004年Clerc等人从量子力学角度出发,修改PSO算法中的粒子“进化”历程,即按照新的路径更新粒子位置,形成QPSO算法.一般的PSO算法不能保证概率1收敛到全局最优解,这也是该算法的不足之处.但是,量子粒子群算法能够解决上述问题,保证粒子能够在全局范围内寻找到最优值[4].
在QPSO中,粒子群对各个粒子位置进行更新,其表达式为
(1)
PPij(t)=fij(t+1)Pij(t)+
(1-fij(t+1))Pgj(t)
(2)
Xij(t+1)= PPij(t)+Rand(t+1)a(t+1)·
|mbestj(t+1)-Xij(t)|·
(3)
(4)
式中:fij(t+1)=ranf(),uij(t+1)=ranf(),用于产生一个随机数,服从均匀分布,大小介于[0,1]之间;M为粒子总数;D为粒子的维数;Pi(t)为第i个粒子在第t次迭代时的当前最优位置;Pg(t)为第t次迭代时粒子的全局最优位置;mbest(t+1)为粒子群中所有粒子第t次迭代时当前最佳位置pbest(t)的中间位置;PPij(t)为Pi(t)和Pg(t)之间的随机点;a(t)为QPSO的收缩扩张系数.a(t)可以取一常数,保持不变,也可以按照式(5)取值,即
(5)
式中,通常取m=1,n=0.5,maxTimes为迭代的最大次数.按照上述方式取值后,a(t)的值将随着迭代次数的增加,线性地从m递减到n.
对于N维空间和M个粒子的最优化问题,目标函数为
minF(θ),θ=(θ1,θ2,…,θn)
s.t.θ∈Rn|θmin,i≤θi≤θmax,i,∀i=1,2,…,n
(6)
式中:θ为待优化问题中需要识别的量;θmin,i和θmax,i为参数θ的最小值和最大值.
在量子粒子群算法中,第i个粒子位置为Xi=(xi1,xi2,…,xin);个体最优位置为Pi=(pi1,pi2,…,pin);全局最优位置为G(t)=(G1(t),G2(t),…,GN(t)),计算公式为G(t)=Pg(t),g=argmin{f[Pi(t)]}.
量子粒子群算法中的粒子位置将根据式(3)而不断变化调整,当满足终止条件或者找到了全局最优解时,停止迭代.其中,算法计算过程[5]如图2所示.
分数阶PIλDμ控制器是将分数阶理论和传统PID控制相结合而提出的控制器,可以看作是传统PID控制的一般化,既继承了传统PID控制的优点,又在此基础上有所发展[6],其时域表达式为
(7)
式中:λ>0为积分阶次;μ>0为微分阶次;Kp、Ki、Kd分别为控制器的控制参数,与传统PID的比例、积分和微分的意义一样;![]() 为Caputo定义.由式(7)可知,分数阶PIλDμ控制器比传统PID控制多两个参数,即积分阶次λ和微分阶次μ.因此,其控制效果和鲁棒性均有了很大提高,实际上,分数阶PIλDμ控制器是一个无限维数的滤波器,其设计原理是根据系统的控制性能指标和闭环特征方程的零极点来设计和优化控制参数的.
为Caputo定义.由式(7)可知,分数阶PIλDμ控制器比传统PID控制多两个参数,即积分阶次λ和微分阶次μ.因此,其控制效果和鲁棒性均有了很大提高,实际上,分数阶PIλDμ控制器是一个无限维数的滤波器,其设计原理是根据系统的控制性能指标和闭环特征方程的零极点来设计和优化控制参数的.
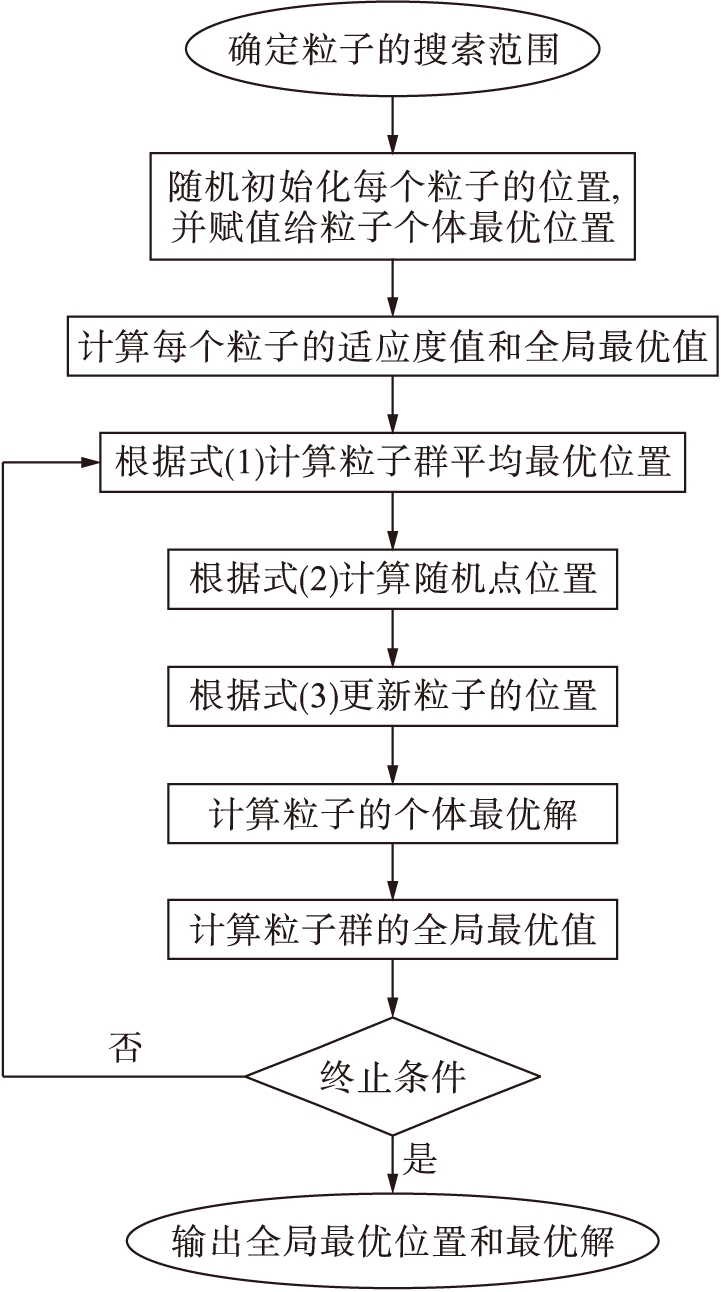
图2量子粒子群算法流程图
Fig.2Flowchartofquantum-behavedparticleswarmalgorithm
由拉普拉斯变换可得
(8)
由式(7)、(8)可以推出分数阶PIλDμ控制器的传递函数为
G(s)=Kp+Kis-λ+Kdsμ
(9)
借助Simulink仿真软件搭建分数阶PIλDμ控制器模块,该模块根据文献[7]介绍的Oustaloup算法进行建模.
针对传统PID控制在跳汰机上的不足,本文设计了量子粒子群算法优化的分数阶PIλDμ控制器(QPSO-FOPID).一方面,该控制器利用分数阶PIλDμ控制器相角范围广,快速性好,精度高等特点来替换传统PID控制器,实现了PID控制从点控到面控的推广;另一方面,针对分数阶PIλDμ里面的参数,引入了量子粒子群算法,实现参数的在线调整,从而使控制系统获得良好的性能指标,其结构如图3所示.
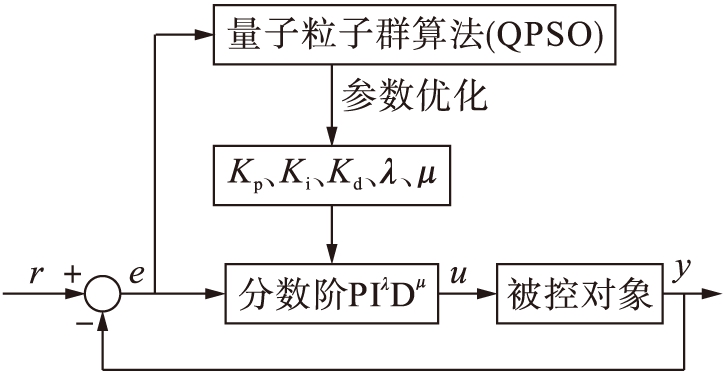
图3QPSO优化的分数阶PIλDμ控制器
Fig.3FractionalorderPIλDμcontrollerwithQPSOoptimization
本文对于跳汰机排料系统的量子粒子群算法优化的分数阶PIλDμ控制器参数,采用的指标为ITAE指标,即时间与绝对误差乘积积分的指标,它能综合体现系统的偏差和时间之间的关系,其值越小越好[8],表达式为
J=![]() t|e(t)|dt
t|e(t)|dt
(10)
以文献[9]得出的矿井跳汰机排料系统作为研究对象,其传递函数为
(11)
系统在时间t=0 s产生单位阶跃响应.采用QPSO算法寻优后得出的跳汰机分数阶PIλDμ控制系统的最优参数分别为Kp=380.320 5、Ki=0.315 2、Kd=8.034 1、λ=0.354 2、μ=0.812 6,其中,QPSO算法的主要参数为:M=60,D=5,maxTimes=30,最优性能指标为J=0.195 6.传统PID控制器的参数是利用传统的Z-N临界比例度法和经验试凑法得出的最优值,即Kp=158.563 0,Ki=0.428 2,Kd=10.450 0.QPSO优化过程中适应度值变化曲线和系统仿真结果如图4~6和表1所示.
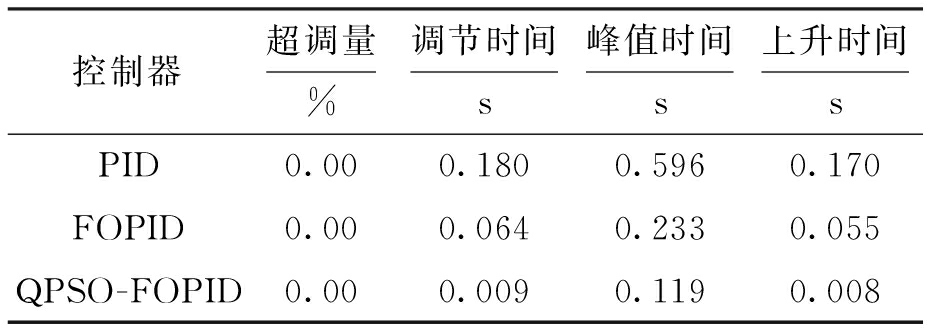
本文针对跳汰机控制系统分别采用传统PID控制、分数阶PIλDμ(FOPID)控制和基于量子粒子群算法优化的分数阶PIλDμ(QPSO-FOPID)控制进行对比分析.根据跳汰机控制系统的实际仿真结果可以明显看出,量子粒子群算法优化的分数阶PIλDμ控制与分数阶PIλDμ控制和常规PID控制相比,其超调量减小,而且调节时间、峰值时间和上升时间等都明显缩短,稳态误差较小,控制精度较高,不仅具有较好的动态响应性能,还有较强的扰动抑制能力,能够提高跳汰机控制系统的控制性能.
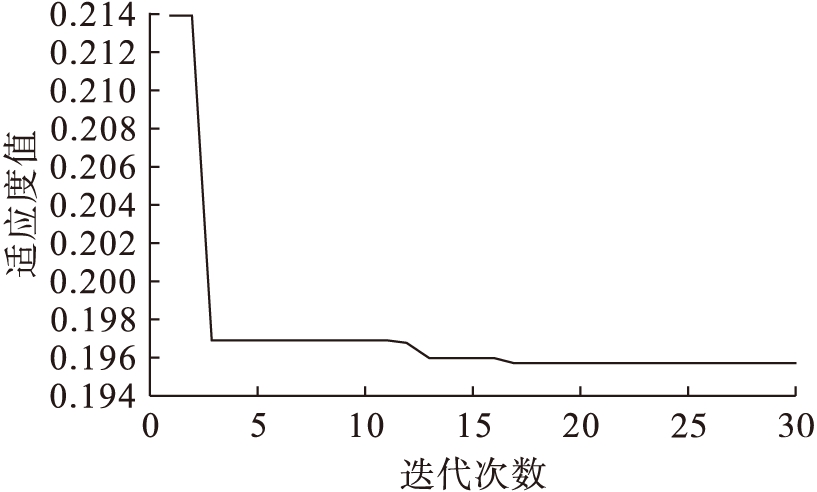
图4适应度值变化曲线
Fig.4Changecurveoffitnessvalue
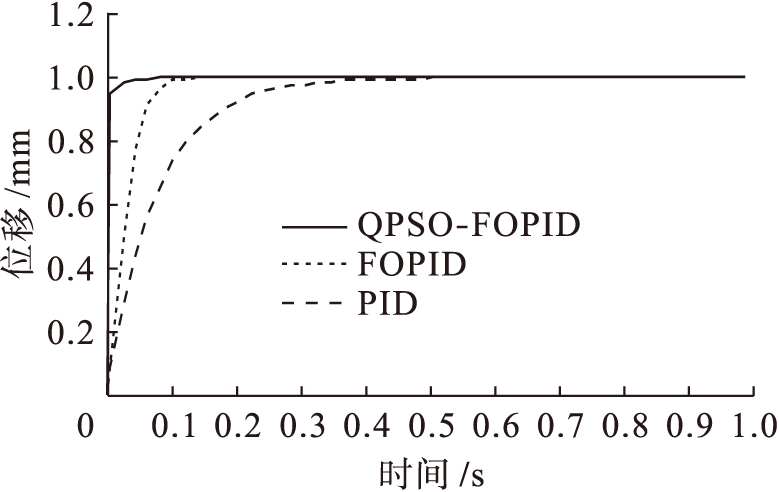
图5系统单位阶跃响应曲线
Fig.5Unitstepresponsecurvesofsystem
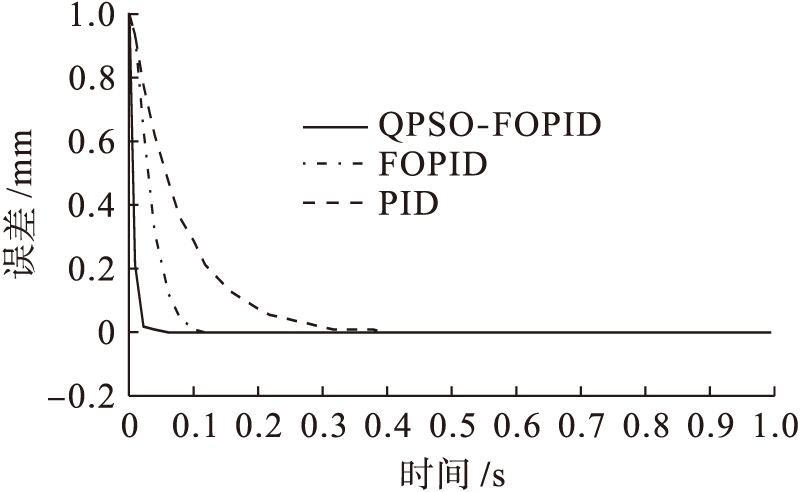
图6系统单位阶跃误差响应曲线
Fig.6Unitsteperrorresponsecurvesofsystem表1不同控制器的动态性能指标比较
Tab.1Comparisonindynamicperformanceindexesofdifferencecontrollers
分数阶PIλDμ控制器可以看成是广义的传统PID控制器,它不仅克服了传统PID的不足,还继承了传统PID控制的优点.针对其参数的调整,本文提出了基于QPSO算法优化的分数阶PIλDμ控制器,实现参数的在线调整,能够对跳汰机排料系统进行有效控制.仿真结果表明,QPSO算法优化的分数阶PIλDμ控制器能够使跳汰机系统获得最佳的控制性能.
参考文献(References):
[1] 孟亚辉.煤炭分选跳汰机排料系统PID控制仿真 [J].煤炭技术,2015,34(12):267-269.
(MENG Ya-hui.Simulation of PID control of jig discharging system optimized by genetic algorithm [J].Coal Technology,2015,34(12):267-269.)
[2] 聂磊.基于粒子群优化的跳汰机风阀优化控制技术研究与设计 [D].赣州:江西理工大学,2015.
(NIE Lei.Based on particle swarm optimization jig air valve control technology research and design optimization [D].Ganzhou: Jiangxi University of Science and Technology,2015.)
[3] 高玉琪.基于模糊PID的跳汰机排料控制的仿真实验研究 [J].煤矿机械,2014,35(6):74-76.
(GAO Yu-qi.Simulation study on jigger discharging system based on fuzzy PID conrtol [J].Coal Mine Machinery,2014,35(6):74-76.)
[4] 孙俊,方伟,吴小俊,等.量子行为粒子群优化:原理及其应用 [M].北京:清华大学出版社,2011.
(SUN Jun,FANG Wei,WU Xiao-jun,et al.Quantum-behaved particle swarm optimization:principle and app-lication [M].Beijing:Tsinghua University Press,2011.)
[5] Chai Z L,Sun J,Cai R,et al.Implementing quantum-behaved particle swarm optimization algorithm in FPGA for embedded real-time applications [C]//Proceedings of Fourth International Conference on Computer Sciences and Convergence Information Technology.Seoul,Korea,2009: 886-890.
[6] 吴振宇,赵亮,冯林.基于分数阶PID控制器的智能车控制 [J].控制工程,2011,18(3):401-404.
(WU Zhen-yu,ZHAO Liang,FENG Lin.Intelligent vehicle control based on fractional PID controller [J].Control Engineering,2011,18(3):401-404.)
[7] 车树涛.分数阶PIλDμ蒸汽压力控制系统算法研究 [D].哈尔滨:哈尔滨理工大学,2012.
(CHE Shu-tao.Research on algorithm of the steam pressure system controlled by fractional-order PIλDμ[D].Harbin:Harbin University of Science and Technology,2012.)
[8] 夏华凤,张中国,刘艳君.船舶锚机控制系统量子粒子群优化PID算法的研究 [J].电工电气,2016(1):25-29.
(XIA Hua-feng,ZHANG Zhong-guo,LIU Yan-jun.Study on PID algorithm based on quantum-behaved particle swam optimization used in ship windlass control system [J].Electrotechnics Elactric,2016(1):25-29.)
[9] 吕亭亭,马小平,陈力.基于遗传算法优化的跳汰机排料系统PID控制仿真 [J].工况自动化,2013,39(1):68-70.
(LÜ Ting-ting,MA Xiao-ping,CHEN Li.Simulation of PID control of jig discharging system optimized by genetic algorithm [J].Industry and Mine Automation,2013,39(1):68-70.)
MA Yue-jun, ZHANG Xiang-yu
(College of Mechanical and Equipment Engineering, Hebei University of Engineering, Handan 056038, China)
Abstract:Aiming at the fact that the traditional PID control in the complex discharge system of jigger has such problems as low control precision, slow response speed and inaccurate parameter adjustment, a fractional order PIλDμcontroller based on the QPSO algorithm optimization (QPSO-FOPID) was proposed. With the fractional order calculus theory, the traditional PID control was generalized from the integer order to the plural order with the proposed controller, and the degrees of freedom of two parameters were increased. At the same time, the parameters for the fractional order PIλDμcontroller were optimized with the quantum-behaved particle swarm optimization (QPSO) to solve the problem of imprecise parameter adjustment. With taking the discharge system of jigger for a certain mine as an example, the Simulink simulation model for the discharge system of jigger was established. The simulation results show that the proposed method can not only realize the online optimization of fractional order PIλDμcontrol parameters, but also has the advantages such as the fast convergence, strong robustness, good dynamic and static performance, no overshoot and high control accuracy.
Keywords:jigger; discharge system; fractional order calculus theory; quantum-behaved particle swarm optimization; PID controller; fractional order PIλDμcontroller; online optimization.
doi:10.7688/j.issn.1000-1646.2018.05.17
* 本文已于2018-04-18 14∶21在中国知网优先数字出版. 网络出版地址: http:∥kns.cnki.net/kcms/detail/21.1189.T.20180418.1050.006.html
作者简介:马玥珺(1977-),女,河北邯郸人,讲师,硕士,主要从事机械制造和机电一体化技术等方面的研究.
基金项目:河北省教育厅基金资助项目(QN2017034).
收稿日期:2017-04-13.
文章编号:1000-1646(2018)05-0577-05
文献标志码:A
中图分类号:TD 445.7
(责任编辑:钟 媛 英文审校:尹淑英)