
图1高架桥Y型桥墩
Fig.1Ytypebridgepierofviaduct
李艳凤1, 罗威力1, 梁 力2
(1. 沈阳建筑大学 交通工程学院, 沈阳 110168; 2. 东北大学 土木工程研究所, 沈阳 110004)
摘要:针对强震下预应力混凝土Y型桥墩的损伤问题,以某市二环路改造工程预应力混凝土Y型桥墩为研究对象,提出了该桥墩的损伤变形及耗能机理,并对其进行了分析.结果表明:强震下Y型桥墩变截面处会出现过多的应力集中,从而导致U形槽区域率先发生损伤,并致使墩柱内力重分布;轴压力的增加会加快墩柱的塑性变形,残余应变增大;横桥向会吸收较多的地震能量,但不能承受过多的位移变化;加固Y型桥墩的U形槽区域,减少桥墩的配重,增加桥墩截面刚度和强度可以有效地提高Y型桥墩的抗震能力.
关键词:Y型桥墩; 预应力混凝土; 损伤变形; 耗能机理; 轴压力; 有限元模拟; 弹塑性变形; 抗震能力
近年来,国内外学者对钢筋混凝土桥墩进行了大量的研究工作,取得了许多有意义的研究成果[1-7].相对已经失效了的《公路工程抗震设计规范》,交通部自2008年10月1日执行的《公路桥梁抗震设计细则》在抗震设计理念、思路要领和地震作用取值等方面均有很大的不同和改善,对于墩柱抗震增加了6.2节梁桥延性抗震设计和6.8节能力保护构件计算的有关规定,增加了8节延性构件细节设计的有关规定,但针对预应力混凝土Y型桥墩并未提出相关设计理论和具体构造措施,如塑性铰区域的划分等[8-11].因此,依然存在以下问题:强震下,预应力混凝土Y型桥墩受损构件的位置和破坏程度等指标与结构整体性能退化规律之间的研究鲜有涉及,破坏机理研究尚未明确.
导致桥墩结构倒塌破坏和结构使用功能降低的主要原因是地震动产生的损坏.地震下桥墩的倒塌破坏不仅取决于桥墩最大能承受的变形,还取决于与桥墩受低周疲劳效应所产生的损伤累积.结构的最大变形和累积的损伤参数通常可用来描述结构的塑性性能,因此,本文拟在Y型桥墩的本构模型里加入损伤参量.开展强震作用下预应力混凝土Y型桥墩弹塑性地震反应研究,并进行预应力混凝土Y型桥墩破坏全过程模拟,系统分析强震作用下结构整体性能退化规律和损伤破坏特性,对损伤破坏机理进行深入研究,以期提高预应力混凝土Y型桥墩结构的抗震能力.
某市二环路改造工程全线采用预应力混凝土Y型桥墩,如图1所示.墩底截面尺寸为160 cm×500 cm,两墩肢截面尺寸为160 cm×190 cm,桥墩墩身材料为C40混凝土,墩身采用HRB335钢筋,桥墩的横向联系梁采用按交错单端张拉方式排列预应力JL32筋的预应力混凝土构件.

图1高架桥Y型桥墩
Fig.1Ytypebridgepierofviaduct
桥墩混凝土的参数如下:混凝土为C40,泊松比为0.166 7,弹性模量为3.25×104MPa,容重为26 kN/m3.预应力精轧螺纹钢筋的参数如下:张拉吨位为632 kN,泊松比为0.3,弹性模量为1.95×105MPa,容重为82 kN/m3,标准强度为930 MPa.
假定混凝土和钢筋之间是理想粘结,选用ABAQUS有限元仿真软件进行理想弹塑性模型的模拟,并使用ABAQUS/Standard进行求解,混凝土构件取20节点六面体单元C3D20R,钢筋取两节点三维桁架单元T3D2,模型如图2所示.
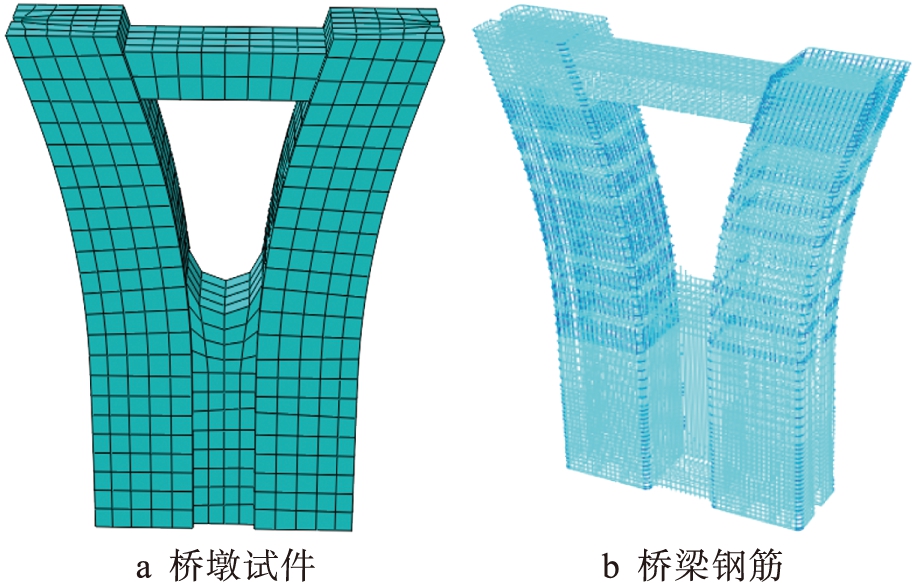
图2Y型桥墩有限元模型
Fig.2FiniteelementmodelforYtypebridgepier
在混凝土构件受力直到损伤的过程中,是弹性到弹塑性变形的过程,在应变时可看作弹性材料,弹性模量不变为E,为弹性段;当应力高出屈服应力时为硬化段,此时构件的变形分为弹性应变和塑性应变,卸载时,弹性应变可恢复,塑性应变不可恢复,从而形成残余应变,随着应变的增大,应力是先增大后减小,应力跨越最大应力值之后开始产生损伤.一般来说,当应力减小到极限应力的80%时,为应变软化段,并引起混凝土结构应变的局部化,可认为构件破坏.
上世纪90年代由Lee、Fenves和Lubliner所创立的混凝土损伤塑性理论是目前ABAQUS所采用的损伤塑性模型的基础,其模型通过各向同性屈服理论来表述非弹性行为,混凝土材料选用不同的损伤因子来描述受压和受拉状态下的刚度退化,并假设混凝土材料的损伤是由拉伸和压缩开裂造成的.鉴于此,引入塑性变形下损伤因子的概念来确定基于规范提供的混凝土本构关系的塑性本构关系参数.
损伤塑性模型(即CDP模型)在进行塑性分析时,需要指定应变和损伤因子的关系,混凝土的弹塑性变形公式为
σ=(1-d)E0(ε-εpl)
(1)
式中:E0为混凝土刚度;d为损伤因子,0<d<1,d=0时为无损伤材料,d=1时为完全损伤材料;εpl为等效塑性应变.由式(1)可知:1)在拉伸和压缩变形后,由于塑性形变的产生,混凝土的刚度不再是原来的E0,而变化为![]() 和
和![]() 分别表示压缩和拉伸等效塑性应变,其值大于0,ABAQUS定义拉伸和压缩的破坏依据是开裂应变
分别表示压缩和拉伸等效塑性应变,其值大于0,ABAQUS定义拉伸和压缩的破坏依据是开裂应变![]() 和非弹性应变
和非弹性应变![]() 其关系式分别为
其关系式分别为
(2)
(3)
建立本构关系的重要环节是损伤因子d的变化规律,其表达式为
(4)
式中,η为塑性应变与非弹性应变的比例系数,拉伸和压缩时η的取值不一样,拉伸时取0.50~0.95,压缩时取0.35~0.70.在做构件的拉压试验时得到的应力应变数据为名义上的数据,在大变形过程中,又不可忽略构件截面面积的改变,故引入真实应力和真实应变,即
(5)
(6)
式中:F为加载荷载;A为试件初始截面面积;l为试件长度;σnom为截面应力;εnom为构件应变.
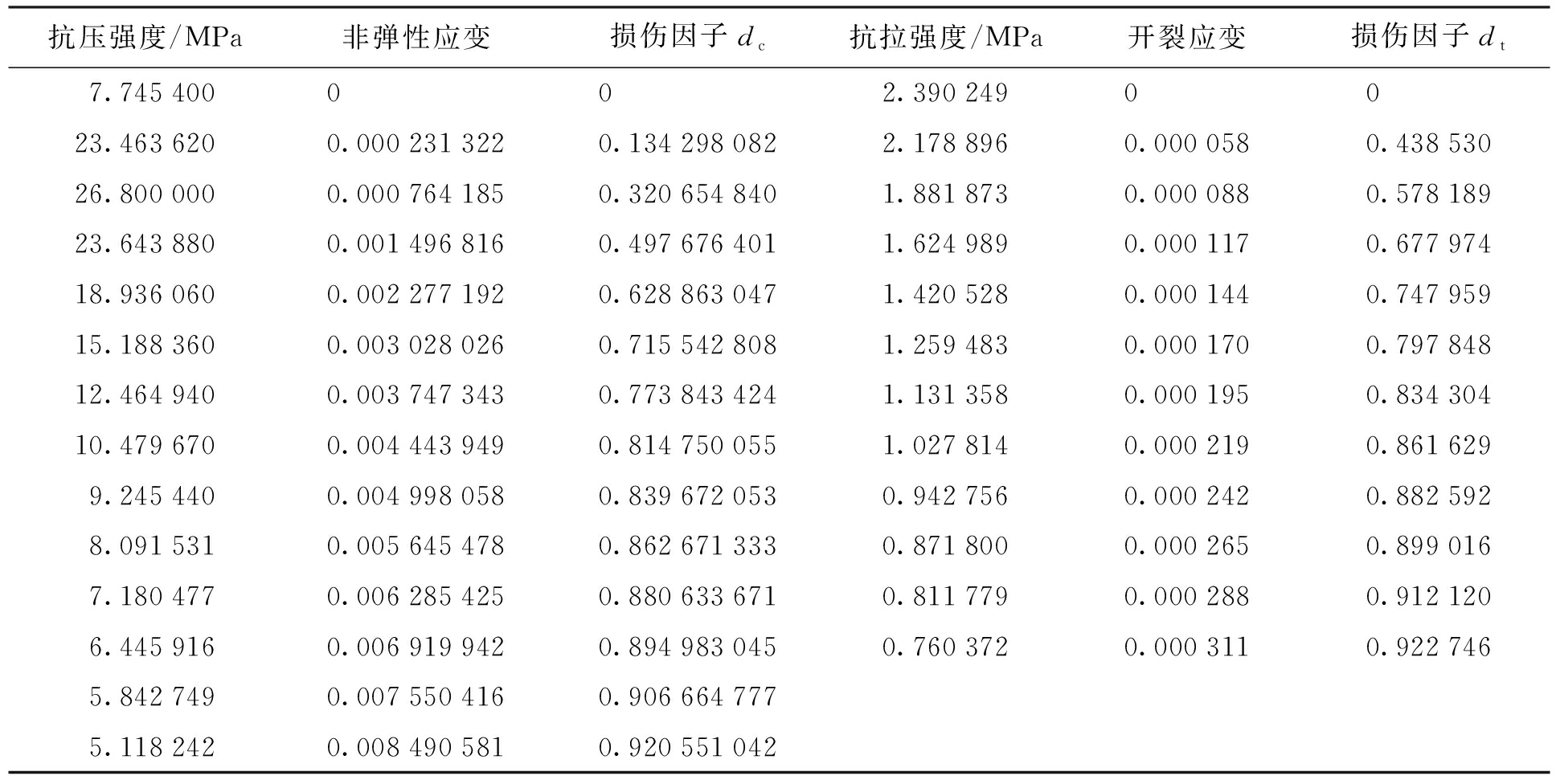
根据上述公式以及C40混凝土材料的性质,可知构件在塑性阶段之后,CDP模型的应力应变曲线参数如表1所示.
表1C40混凝土计算参数
Tab.1CalculationparametersforC40concrete
地震时,经过往复荷载作用,在弹塑性变形下,构件往往经过几十次的往复循环才会倒塌,也就是构件的累积损伤破坏,微小的局部破坏到全部倒塌也需要一个过程.基于Lee-Fenves损伤模型,即CDP模型,可较好地应用于模拟循环加载的情况,但不适用于对于混凝土结构非线性地震响应分析的需求,因此,在不改变子程序的情况下,隐式求解器并不能用于计算现有的地震波,故采用等效的push-over法来模拟桥墩在强震下的低周往复运动,为了更贴合墩身的实际运动,依次在桥墩的顺桥向和横桥向两个方向进行推覆,进而分析其地震下的损伤机理.位移加载的幅值与屈服位移的选定有关,屈服位移以内的混凝土构件可看作是弹性材料,可不做损伤研究.为了避免不必要数据,在制订位移加载制度之前首先进行试件的单推模拟,得到的数据曲线如图3所示.
结合桥墩的墩顶位移与曲率分布成一定的积分关系,如果等效塑性铰的长度已知,墩顶位移也可以由基于塑性铰模型的考虑截面矩形曲率的计算公式求出,可以假设塑性铰位置最先出现在墩底部,从而对墩顶位移进行简便的估算,其表达式为
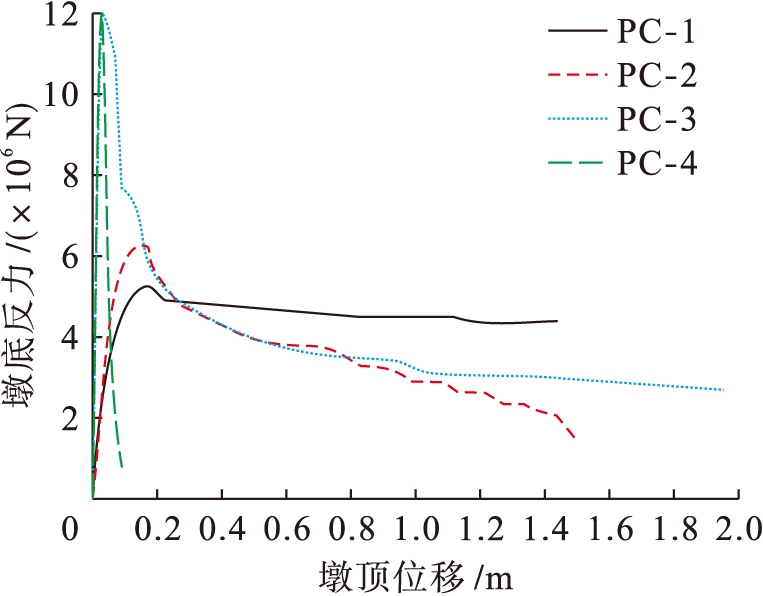
图3试验组单推曲线
Fig.3Singlepushcurvesoftestgroups
(7)
式中:Δ为总位移;Δe为弹性位移;Δp为塑性位移;φe为弹性曲率;φ为总曲率;Lp为等效塑性铰长度;L为构件的长度.
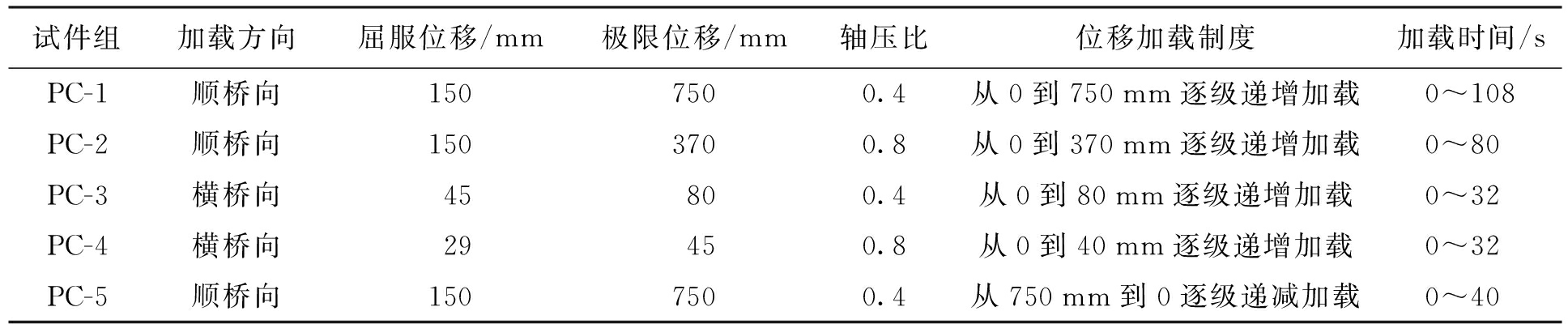
基于上述方法确定了桥墩在试验时所承受的屈服状态下和极限状态下的位移.为了尽可能地模拟桥墩在强震下的破坏规律,在借鉴前人的基础上通过不断地调试方案,最终采用的试验方法如表2所示.为了更好地研究塑性铰的变化规律,增加一组PC-5试件的加载制度,PC-5组是对比试验组,目的是探究急速大变形下对桥墩损伤的影响.
表2试验组的加载方案
Tab.2Loadingschemesfortestgroups
3.3.1 塑性铰结果分析
桥墩的弯曲性能可假设为理想的弹塑性模型,延性是结构在承载能力无明显减小的条件下承受变形的能力,延性和塑性铰的长度存在联系,在反复力的作用下,墩身产生转动,致使弯矩达到弹性弯矩的极限时,转动从弹性进入了弹塑性,可认为此处形成了塑性铰.根据国内常采用的经验公式,塑性铰长度等于0.022倍的纵筋直径与屈服强度的乘积然后加上0.08倍的构件长度.
对5组试件在不同的推覆模拟试验中进行了比较,在控制荷载下,损伤参量云图的场分布如图4~8所示.在ABAQUS的隐式计算中,模型的截面处达到最大损伤参量值时,则不再提升,可认为此处截面所承载的弯矩达到其所能抵抗的极限弯矩,截面曲率也达到极限曲率,因此,用混凝土的损伤参量来判断塑性铰的变化情况.
通过塑性铰产生的顺序和其变化快慢来描述桥墩损伤破坏的规律.
1) 通过对比图4~8,分析塑性铰的产生顺序:PC-1试件在0 s时顶端产生初始损伤,20 s时底端开始出现塑性铰,之后损伤沿底端U形槽区域发展直至形成贯通损伤区域;PC-2试件塑性铰的产生顺序和PC-1试件相同;PC-3试件在0 s时顶端产生初始损伤,10 s时两肢臂、U形槽区和底端两侧几乎同时出现塑性铰,之后肢臂处的塑性铰继续向周围扩大,U形槽处的塑性铰向下发展,底端两侧的塑性铰发育则不太明显;PC-4试件塑性铰的产生顺序和PC-3试件相同;PC-5试件塑性铰的产生顺序和PC-1、PC-2试件相同.
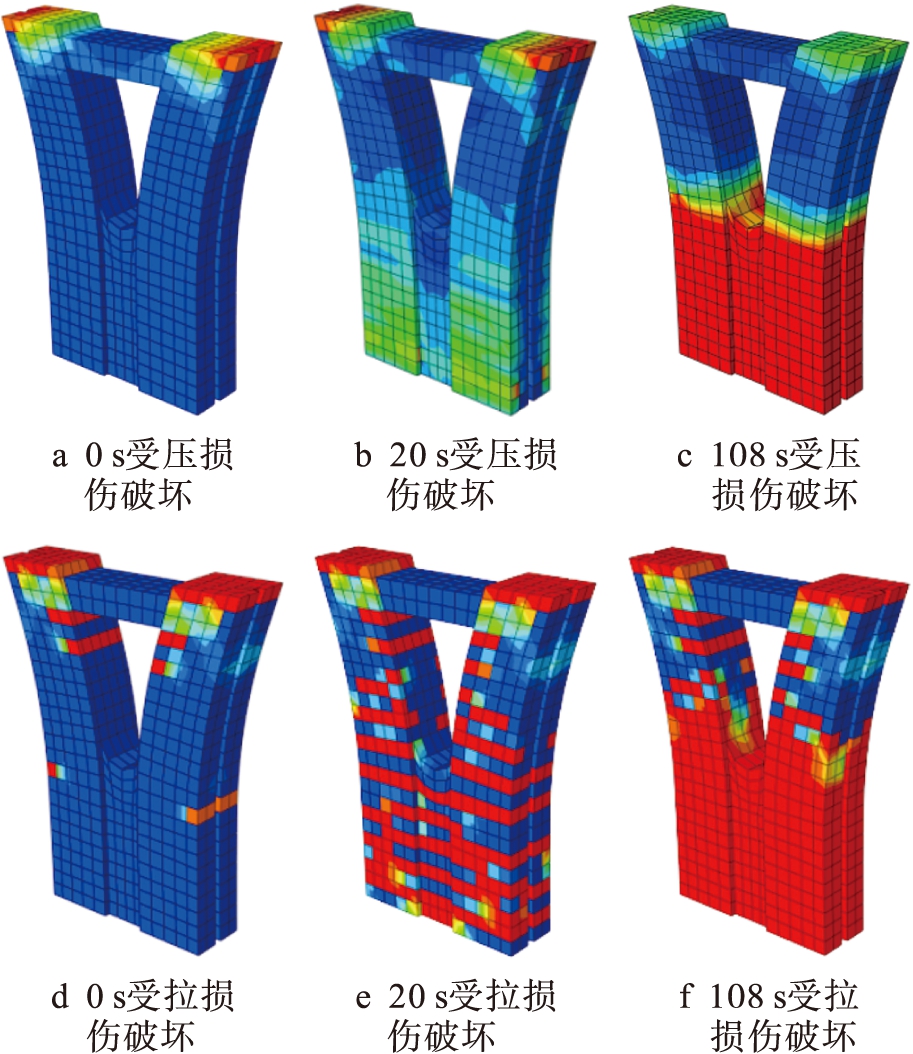
图4PC-1试验组损伤参量云图
Fig.4DamageparameterdiagramofPC-1testgroup
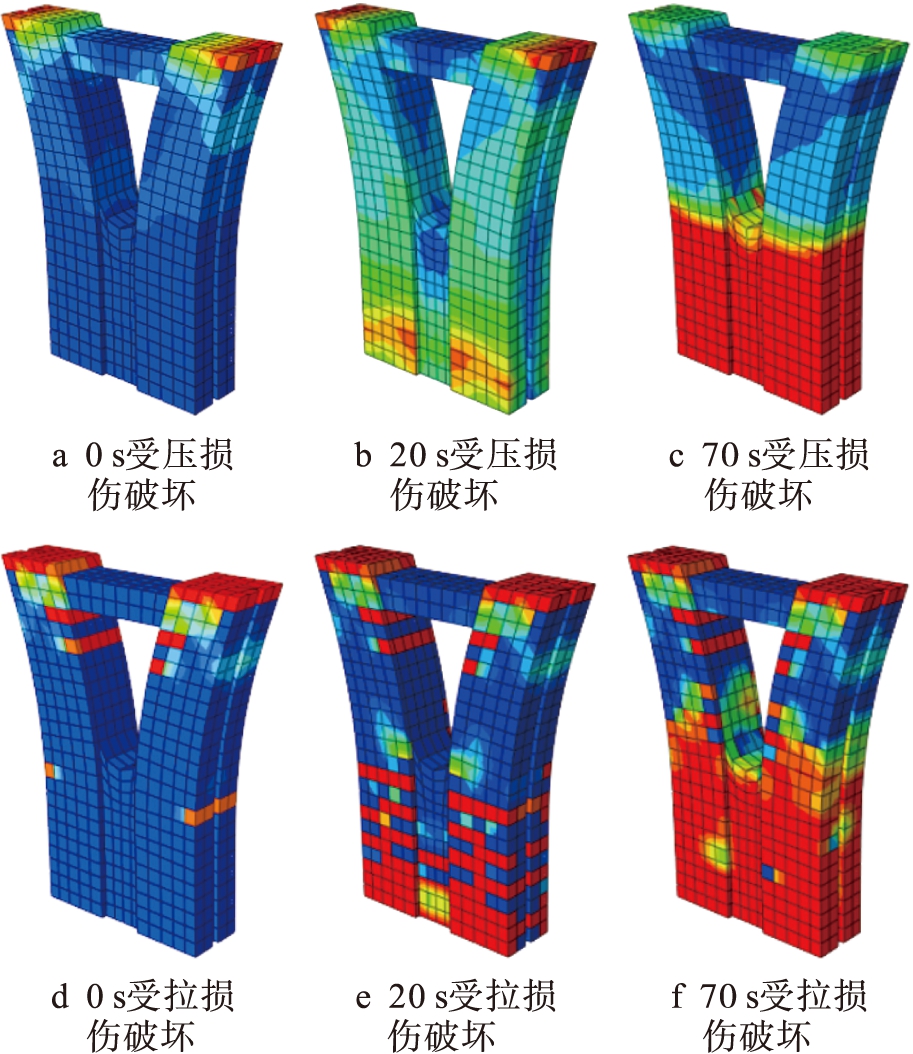
图5PC-2试验组损伤参量云图
Fig.5DamageparameterdiagramofPC-2testgroup
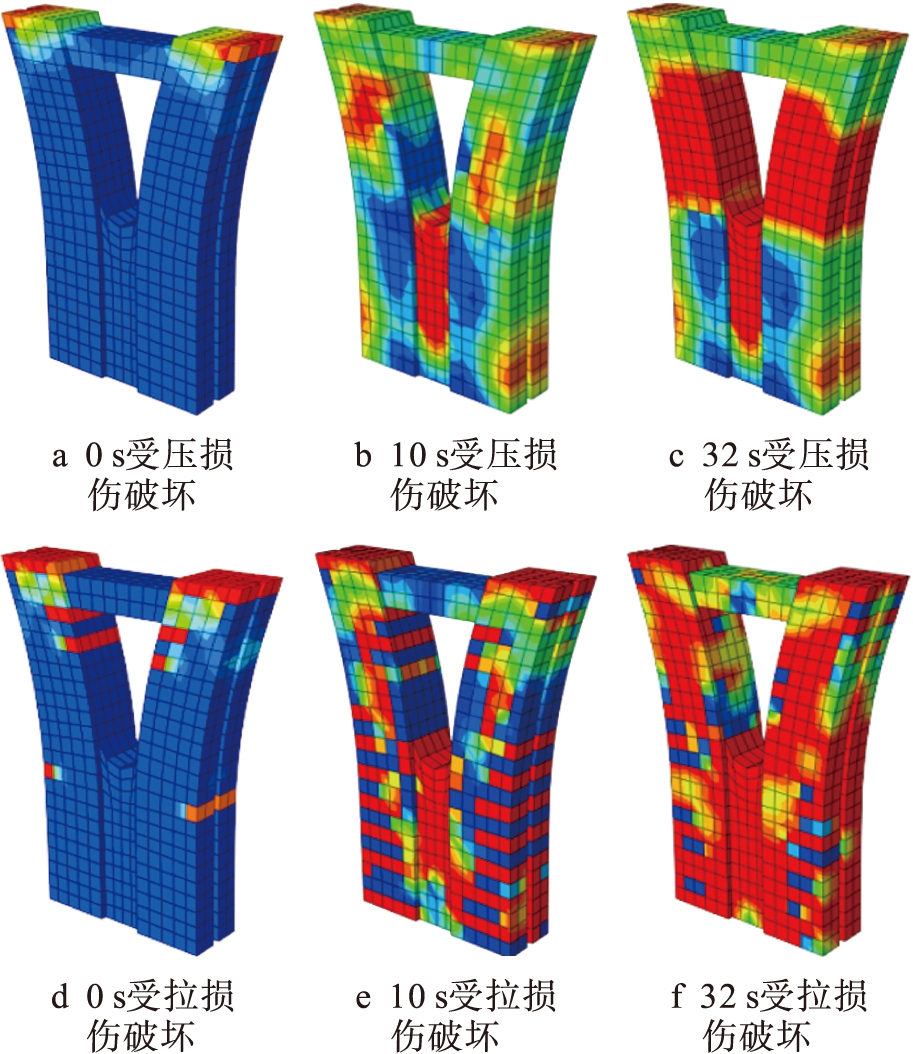
图6PC-3试验组损伤参量云图
Fig.6DamageparameterdiagramofPC-3testgroup
2) 就塑性铰的变化快慢而言,5组试件的塑性变形情况十分接近,参照每组试件的受拉与受压,轴压比和不同加载方向并不能影响塑性铰产生顺序,但会影响塑性铰变化的快慢,轴压比大的试件会较早产生塑性铰(如PC-1比较PC-2、PC-3比较PC-4),横桥向的加载往往较顺桥向先破坏(如PC-1比较PC-3、PC-2比较PC-4);对比试验组PC-5可以看出,逐级递减的幅值加载方案仅仅影响了塑性铰的变化快慢.
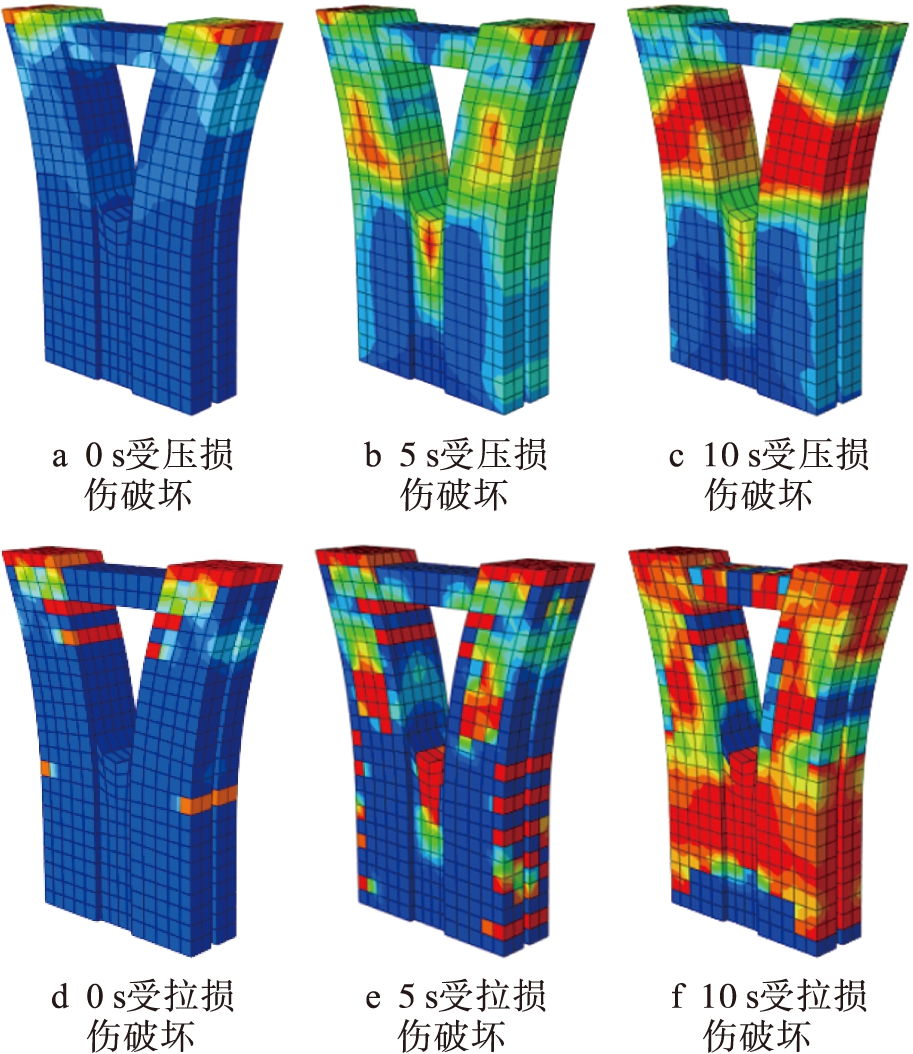
图7PC-4试验组损伤参量云图
Fig.7DamageparameterdiagramofPC-4testgroup
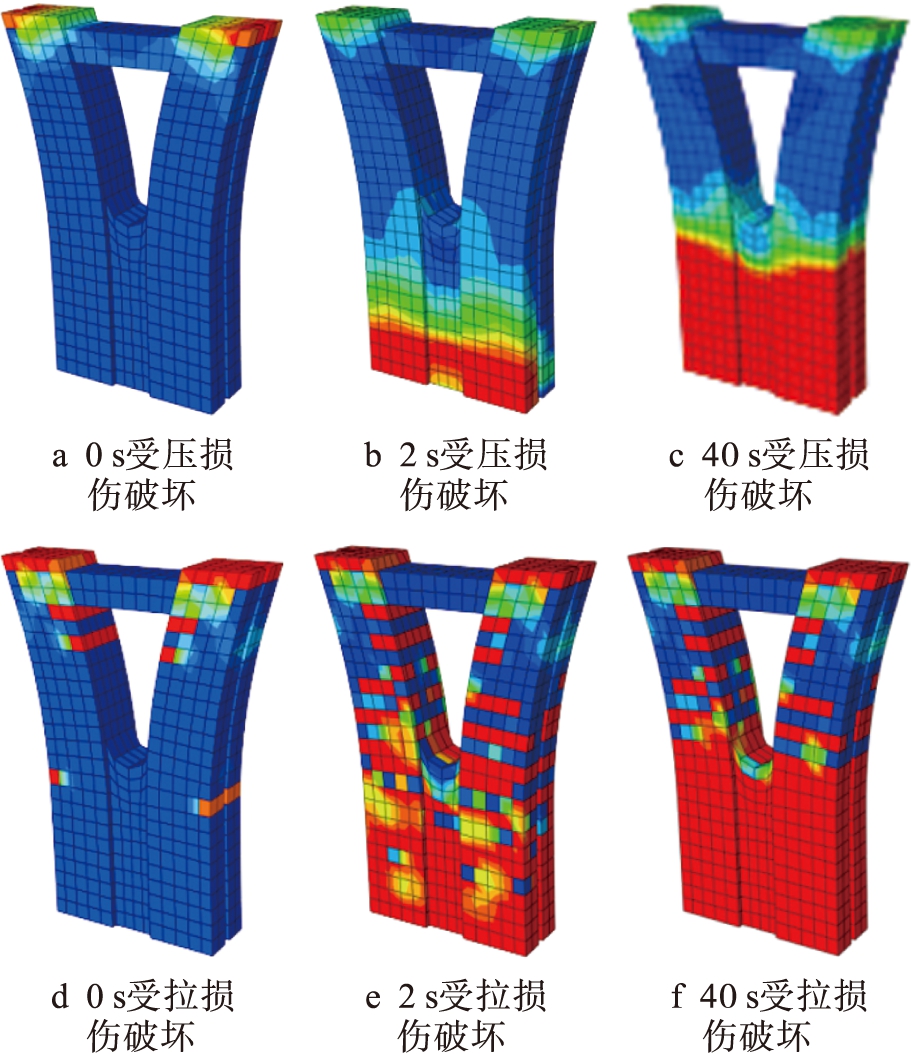
图8PC-5试验组损伤参量云图
Fig.8DamageparameterdiagramofPC-5testgroup
3) 对塑性铰的变化规律进行分析,5组试件的初始损伤均发生在顶端,可看做是由轴压力的作用引起的.在构件变形时,PC-1、PC-2构件的塑性铰优先产生于底端,继而向上发展直至完全破坏;PC-3、PC-4构件底端产生塑性铰时,U形槽内也产生了损伤,之后的塑性发展中两肢臂要明显快于桥墩底部,塑性铰发育的速率明显增加,可判断出U形槽由于应力集中引起率先损伤,并导致墩柱内力的重分布,两肢臂承受过多的内力,成为主要耗能点.由于两肢和底端的塑性铰大量形成并充分发育,致使墩柱塑性变形程度进一步增加,整体的抗震性能大幅度降低(如PC-3的受拉损伤破坏).横梁采用JT32的预应力钢筋,截面刚度与两肢段接近,在反复推拉过程中可近似于三角形结构,稳定性较高,而变截面处由于应力集中,则会率先发生破坏.
3.3.2 滞回性能结果分析
在弹塑性阶段之后,结构体系的阻尼耗能和塑性变形是消耗地震总输入能量的两大主要部分,根据能量平衡原则,如果地震动作用于结构的能量能通过结构的塑性变形、阻尼和滞回的方式消耗掉,那么此结构可较好地抵御地震动荷载,不会倒塌破坏.结构体系进入塑性阶段不可恢复,且结构体系有着稳定变化范围的阻尼比,因此,结构体系的破坏能量可用结构的滞回耗能来表示.数值模拟得到的5组试件墩底荷载与墩顶水平位移的滞回曲线如图9所示.
由图9可知,PC-1试件的滞回曲线呈明显的“梭形”,滞回环面积较小;PC-2试件有一定的捏缩现象,滞回环较饱满;PC-3试件滞回包络面积较大,捏缩现象较为严重;PC-4试件滞回包络面积最小,水平反力下降的速度也慢;PC-5试件呈现较为饱满的“梭形”.由分析结果可以看出:顺桥向加载,随着轴压力的增加,滞回的包络面积增大,但是捏拢现象增大,说明轴压力的增加会增加构件的耗能,同时也增大了残余应变,进而降低了耗能能力,吸收地震能量的能力也随之下降;横桥向则反之,说明构件的滞回性能与构件加载方向的截面形状具有一定的关系,构件的耗能能力与轴压力的大小有关.横桥向桥墩在受损伤破坏时的位移变化量比顺桥向要小得多,可知反复推拉试验更容易破坏横桥向桥墩;PC-5试件良好的滞回性能说明在每级递减的位移加载下,构件的塑性变形能力很强,反映出整个构件抗震时在地震波振幅渐小的情况下,耗能能力最强.
Y型预应力混凝土桥墩的承载力在强震下会随着薄弱区域塑性铰的发展而逐步造成墩身的性能退化,耗能能力降低,其承载能力及延性的损失增大,导致其最终损伤破坏,结合数值模拟结果和理论原理,可得出如下结论:
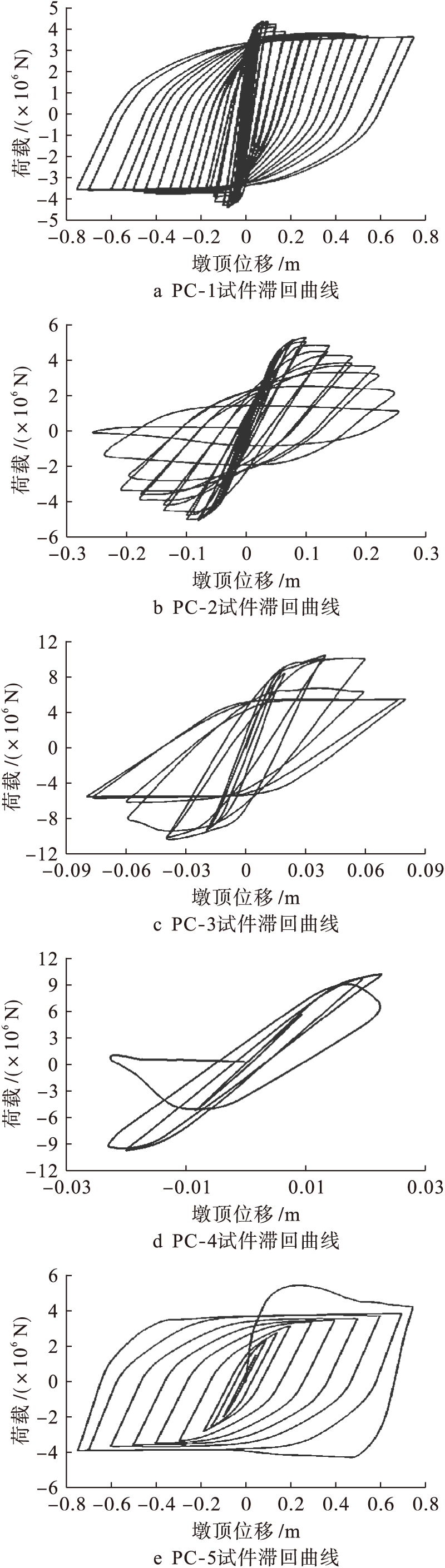
图9不同试验组的荷载![]() 位移滞回曲线
位移滞回曲线
Fig.9Load-displacementhystereticloopsofdifferenttestgroups
1) 强震下桥墩U形槽区域由于应力集中引起率先损伤,并导致墩柱内力的重分布,两肢臂承受过多的内力,成为主要耗能点,底端塑性铰会因为持续的反复力作用而向上移动,直至形成贯通性损伤.
2) 横梁采用JT32的预应力钢筋,截面刚度与两肢段接近,在反复推拉过程中可近似于三角形结构,稳定性较高;而变截面处由于应力集中,则会率先发生破坏.
3) 轴压力的大小影响着构件的塑性铰发育和耗能能力,桥墩塑性变形会随着轴压力的增加而增大,而顺桥向的耗能能力会随之减小,横桥向的耗能能力会随之增大.
参考文献(References):
[1] 李宏男.结构多维抗震理论 [M].北京:科学出版社,2006.
(LI Hong-nan.Structure multidimensional seismic theory [M].Beijing:Science Press,2006.)
[2] 范立础.桥梁工程 [M].上海:同济大学出版社,2012.
(FAN Li-chu.Bridge engineering [M].Shanghai:Tongji University Press,2012.)
[3] Kwasniewski L.Nonlinear dynamic simulations of progressive collapse for a multistory building [J].Engineering Structures,2010,32(5):1223-1235.
[4] 于琦,孟少平,吴京.基于变形与能量双重准则的钢筋混凝土结构地震损伤评估 [J].土木工程学报,2011,44(5):16-23.
(YU Qi,MENG Shao-ping,WU Jing.Deformation and energy-based seismic damage evaluation of reinforced concrete structures [J].Chinese Journal of Civil Engineering,2011,44(5):16-23.)
[5] 丁阳,伍敏,徐龙河,等.钢柱考虑损伤累积效应的强震下损伤演化规律 [J].建筑结构学报,2011,32(7):112-117.
(DING Yang,WU Min,XU Long-he,et al.Seismic damage evolution of steel columns considering da-mage accumulation [J].Journal of Building Structures,2011,32(7):112-117.)
[6] 唐代远,陆新征,叶列平,等.柱轴压比对我国RC框架结构抗地震倒塌能力的影响 [J].工程抗震与加固改造,2010,33(5):26-35.
(TANG Dai-yuan,LU Xin-zheng,YE Lie-ping,et al.Influence of axial compression ratio to the seismic co-llapse resistance of RC frame structures [J].Earthquake Engineering and Reinforcement,2010,33(5):26-35.)
[7] 陆新征,唐代远,叶列平,等.我国7度设防等跨RC框架抗地震倒塌能力研究 [J].地震工程与工程振动,2011,31(5):13-20.
(LU Xin-zheng,TANG Dai-yuan,YE Lie-ping,et al.Study on the seismic collapse resistance of RC frame structures with equal spans in zones with seismic in-tensity Ⅶ [J].Earthquake Engineering and Engineering Vibration,2011,31(5):13-20.)
[8] 丁阳,刘碧文,葛金刚.地震作用下单层柱面网壳倒塌机理分析与试验研究 [J].地震工程与工程振动,2013,33(2):68-73.
(DING Yang,LIU Bi-wen,GE Jin-gang.Collapse mechanism analysis and experiment study of single-layer cylindrical reticulated shells under earthquake action [J].Earthquake Engineering and Engineering Vibration,2013,33(2):68-73.)
[9] Haselton C B,Liel A B,Deierlein G G,et al.Seismic collapse safety of reinforced concrete buildingsⅠ:assessment of ductile moment frames [J].Journal of Structural Engineering,2010,137(4):481-491.
[10] Liel A B,Haselton C B,Deierlein G G.Seismic co-llapse safety of reinforced concrete buildingsⅡ:comparative assessment of nonductile and ductile moment frames [J].Journal of Structural Engineering,2010,137(4):492-502.
[11] Zareian F,Krawinkler H.Structural system parameter selection based on collapse potential of buildings in earthquakes [J].Journal of Structural Engineering,2010,136(8):933-943.
LI Yan-feng1, LUO Wei-li1, LIANG Li2
(1. School of Transportation Engineering, Shenyang Jianzhu University, Shenyang 110168, China; 2. Institute of Civil Engineering, Northeastern University, Shenyang 110004, China)
Abstract:Aiming at the damage problem of Y type prestressed concrete bridge pier under strong earthquake, the Y type prestressed concrete bridge pier of second ring road transformation project in a certain city was taken as the study object, and the damage deformation and energy dissipation mechanism of the bridge pier were proposed and analyzed. The results show that too much stress concentration appears at the variable section of Y type bridge pier under strong earthquake, which leads to the first occurrence of damage in the U shaped groove area and also causes the redistribution of pier column internal force. With increasing the axial pressure, the plastic deformation of the pier column will be quickened, and the residual strain will also increase. The cross-bridge will absorb more earthquake energy, but can not bear too much change of displacement. Through strengthening the U shaped groove area of Y type bridge pier, reducing the counterweight of bridge pier and enhancing the section stiffness and strength of bridge pier, the seismic resistance of Y type bridge pier can be effectively improved.
Keywords:Y type bridge pier; prestressed concrete; damage deformation; energy dissipation mechanism; axial pressure; finite element simulation; elastic-plastic deformation; seismic capacity
doi:10.7688/j.issn.1000-1646.2018.05.19
* 本文已于2018-08-29 14∶02在中国知网优先数字出版. 网络出版地址: http:∥kns.cnki.net/kcms/detail/21.1189.T.20180828.1354.022.html
作者简介:李艳凤(1980-),女,辽宁盘锦人,副教授,博士,主要从事桥梁结构等方面的研究.
基金项目:辽宁省教育厅科学研究一般项目(L2015442); 沈阳建筑大学科研基金资助项目(20150500).
收稿日期:2017-03-20.
文章编号:1000-1646(2018)05-0588-07
文献标志码:A
中图分类号:TM 343
(责任编辑:钟 媛 英文审校:尹淑英)