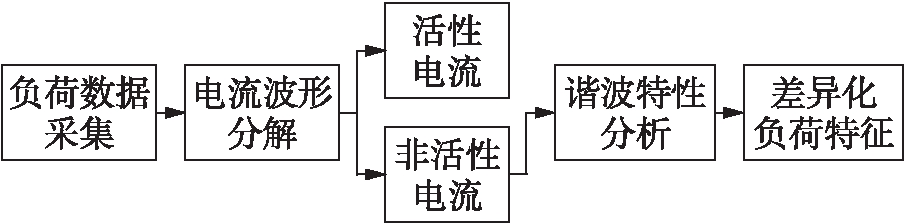
图1 谐波特征提取流程
Fig.1 Flow chart of extraction of harmonic characteristics
电气工程
随着全球能源互联网的建设与发展，我国初步建成了互动化的智能电网服务体系，但电网负荷的急剧增加对智能电网的发展提出了更高的要求[1].智能用电连接了用户侧和电网侧，对整个电网经济高效运行具有较大的影响，是实现智能电网的重要组成部分[2].而实现灵活的智能用电是智能电网的一个主要发展和研究方向[3-4].
智能用电的首要环节是使用负荷监测技术实时采集、分析用户的用电数据，从而实现用户用电细化[5].传统的负荷监测技术主要采集用户的总负荷数据，若能监测用户每一种电器的运行状态，获取更细粒度的运行数据，这对于用户与电网均具有重要意义[6-8].
根据采集装置安装位置的不同可以将负荷监测技术分为侵入式监测和非侵入式监测两种[9-10].侵入式监测系统在安装时需要短暂停电，会干扰用户的正常生活；非侵入式监测通过分解和识别用户的总负荷来获取用电器的类别及使用状态等更细粒度的数据.侵入式监测系统不仅成本高，且不便于维护；而非侵入式的监测系统不仅可以大幅减少硬件与维护成本，还能获取更准确、全面的用电信息[7-10].
基于智能优化算法及其学习算法，专家和学者提出了诸多非侵入式负荷识别算法.如文献[11]中使用神经网络和最小剩余法识别用电器；文献[12]将负荷设备的有功功率和电流值编码组合构建特征，并使用遗传算法寻找最优值，从而确定电器的工作状态；文献[13]通过提取负荷电流的波形特征，得到了较精确的识别结果；文献[14]中使用FastICA算法和多特征参数检测用户的用电器.以上方法从用电负荷的特征提取和分类识别算法两方面进行优化与改进，有效地挖掘用户的用电信息.在电器负荷接近或较小时，利用传统的用电器电流和功率等单一的暂态特征不能得到理想的识别效果.针对上述问题，本文提出了一种基于谐波特征和遗传算法的非侵入式电器负荷识别算法.
非侵入式负荷检测系统中常用的特征可以分为稳态特征和暂态特征两种.其中，一般采用谐波分析和时域分析法提取用户的有功功率、无功功率和电压、电流等稳态特征；采用小波分析和频谱分析提取暂态特征.然而，当用电器的功率、电压和电流等稳态特征具有较高的相似度时，并不能有效地区分不同的用电器，识别效果较差.针对这一问题，本文使用了一种谐波特征提取方法将用户的电流波形分为非活性和活性两部分，以体现不同用电器间的差异性，从而提高识别精度.谐波特征提取流程如图1所示.
图1 谐波特征提取流程
Fig.1 Flow chart of extraction of harmonic characteristics
由文献[14]可知，用电器的电流可分解为非活性电流ia(t)和活性电流ib(t)，即
i(t)=ia(t)+ib(t)
(1)
又由于活性电流ib(t)与电压存在正交关系，即
(2)
(3)
IPW=i(t)u(t)
(4)
式中，Urms为瞬时功率IPW和电压u(t)的均方根.故结合式(1)～(4)可得到非活性电流为
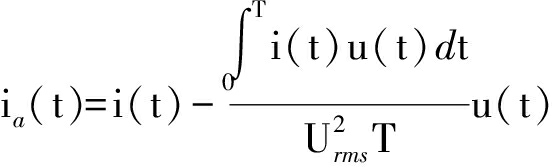
(5)
非活性电流并不向电器负荷传播能量，表示的是与电压正交且与震荡、干扰等影响瞬时功率的因素相关联的电流分量.因不同用电器的干扰因素互不相同，故其间的非活性电流存在着较大的差异.本文使用傅里叶变换分解非活性电流，从而得到非活性电流谐波，即
(6)
本文设置式(6)中T为120 s，并根据采集到的电流、电压和功率值分别计算得到如图2所示的电风扇、电视机和音箱3种低功率电器的非活性电流.
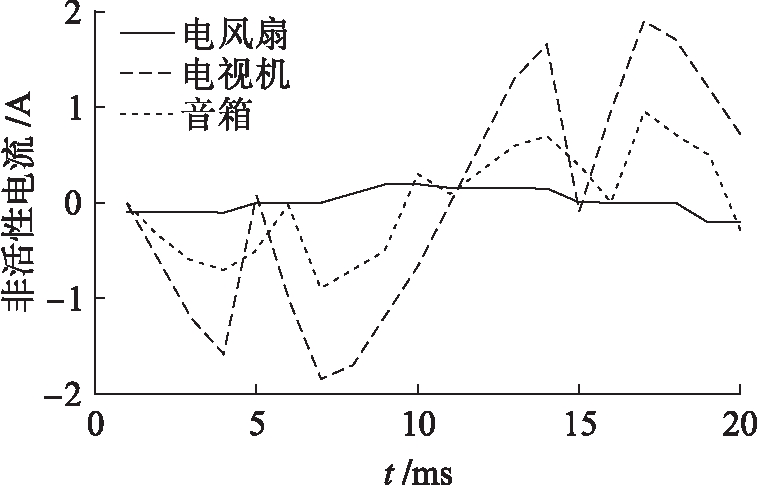
图2 3种低功率电器的非活性电流
Fig.2 Non-active current of three electric appliances with low power
从图2中可以看出，对于电流波形相似的3种电器，其非活性电流波形存在较大差异.提取3种非活性电流的谐波特征，可得到如图3所示的统计结果.由图3也可以看出，3种电器的非活性电流的谐波特性也存在较大差异.
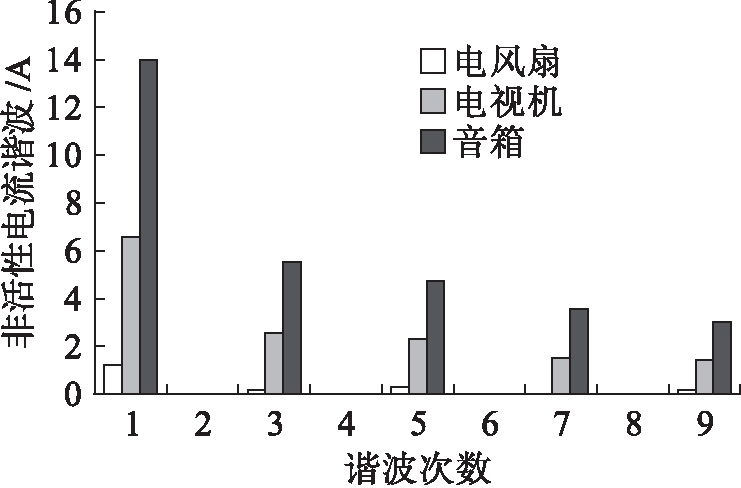
图3 3种电器的非活性电流的谐波特性
Fig.3 Harmonic characteristics of non-active current of three electric appliances
为进一步研究本文提取的非活性电流谐波特征间的差异性，使用相似性度量指标量化比较两种电器a和b的相似程度，即
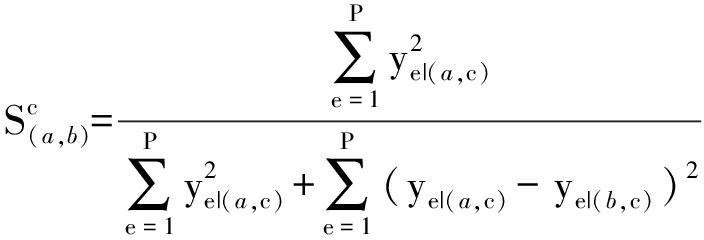
(7)
式中：P为总采样次数；ye|(a，c)为电器a的特征c的第e个采样值.两电器的相似程度越大，得到的
值越大，表明所使用的特征c并不适合负荷的识别.图4分别比较了音箱和电风扇的电流波形、有功功率、电流谐波特征、非活性电流波形和非活性电流谐波的相似度.从图4中可以看出，电风扇与音箱在各种特征中具有较高的相似度.相比于其他3种特征，非活性电流波形及其谐波相似度最低，由此表明，采用非活性电流特征能体现出不同电器间的差异性.
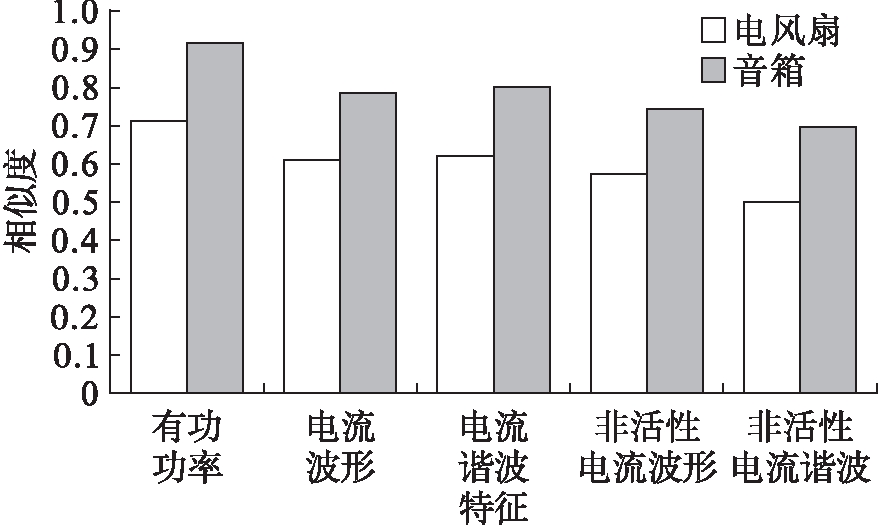
图4 音箱和电风扇各种特征的相似度
Fig.4 Similarity of various characteristics between sound box and electric fan
本部分使用上文提取的非活性电流特征及其他暂态和稳态特征，提出了一种基于遗传算法的负荷识别方法，负荷识别基本流程如图5所示.该算法使用遗传算法优化神经网络权重、阈值和隐含层神经元个数，实现提高负荷识别精度的目的.其中，神经网络的输入为负荷数据的各种特征组合；输出为测试场景的用电器种类，每个输出神经元编码一种电器的开关状态.本文使用网络误差的2范数作为遗传算法的适应度函数及遗传算法的优化目标，求得使误差最小的网络参数.
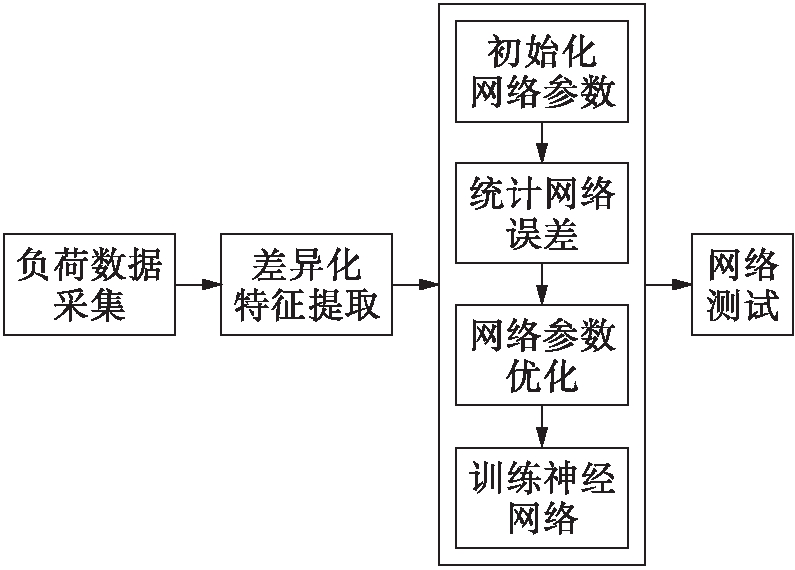
图5 负荷识别算法流程
Fig.5 Flow chart of load identification algorithm
神经网络的权重、阈值和隐含层个数的选择能显著影响其分类性能.传统的神经网络算法先随机初始化网络参数，再使用反向传播算法学习优化网络参数.该方法易受训练样本的影响，易收敛到局部最小值，以至于不能得到最优解.神经网络隐含层节点的选择也极其重要，若设置的节点过多，不仅会增加网络训练耗时，而且会导致网络的泛化能力和容错性能下降.因此，本文使用文献[14]的方法逐步缩小隐含层节点数的取值范围，并使用遗传算法训练得到最优的隐含层数量及神经元的权重与阈值.
设神经网络的M种输入特征构成的特征向量为F(t)=[F1(t)，F2(t)，…，FM(t)]，特征向量的维度等于输入节点数R；两神经元节点i与节点j间的权重为wi，j，节点k的阈值为bk，则神经网络netj(t)隐含层节点j的输入为
(8)
S型正切函数表达式为
(9)
则使用式(8)所示的激活节点j，可得节点j的输出为
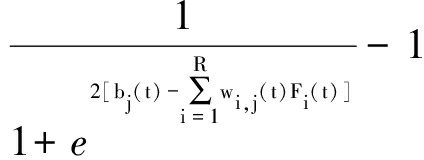
(10)
由式(10)可知，节点j的输出范围为[-1，1].
若使用S型对数函数作为输出神经元的传递函数，即
(11)
则得到的输出值为
Opre(t)= g(netj(t)-bj(t)-bk(t))=
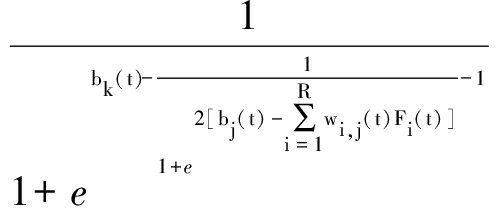
(12)
综上可得神经网络输出误差为
(13)
式中：S2为输出节点数；
为期望输出；
为实际输出.
基于遗传算法的负荷识别流程如下：
1) 采样得到电压和电流等数据的暂态、稳态与谐波特征，并归一化；然后将所有样本数据按4∶1划分为训练集和测试集.
2) 设置输入层、输出层节点数，并计算得到隐含层最大节点数.
3) 根据各层节点数初始化遗传算法的染色体编码设置总迭代次数，种群大小及染色体交叉、变异的概率.
4) 设置遗传算法的适应度函数，并设置迭代停止阈值.
5) 使用训练集样本和初始化的神经网络参数，迭代寻找神经网络的最优参数，直至达到总迭代次数.
6) 使用步骤5)得到的最优参数构建神经网络.
7) 使用测试集样本测试神经网络的性能，并统计分析电器负荷的识别精度.
本文使用Matlab 2017软件进行仿真测试，实验过程选择3种特征作为神经网络的输入，其中包括2种稳态特征：有功功率(P)和无功功率(Q)；1种暂态特征：非活性电流谐波特征(N-Har).由采样得到的电压U、电流I及其夹角θ可得有功功率和无功功率的计算表达式，即
(14)
(15)
本部分使用220V电压母线下的5种常见高功耗和低功耗的家用电器：电视机、音箱、电风扇、热水器和空调进行仿真测试.采样得到200种不同电器使用情况下的特征数据，并使用其中的160组数据构建训练集，剩下的40组作为测试数据，取10次测试结果的平均值作为算法的精度.同时，根据多次试验结果设置遗传算法的种群大小为50，共迭代优化20次，再使用0.7的交叉概率进行单点交叉，变异概率为0.01.
本文将提出的遗传算法优化的神经网络(GA-NN)与BP神经网络(BP-NN)的识别准确率进行了比较，结果如图6所示.由图6可以看出，两种算法的识别准确率均不稳定，GA-NN的最大准确率达到了98%，比传统BP-NN的准确率有所提高.
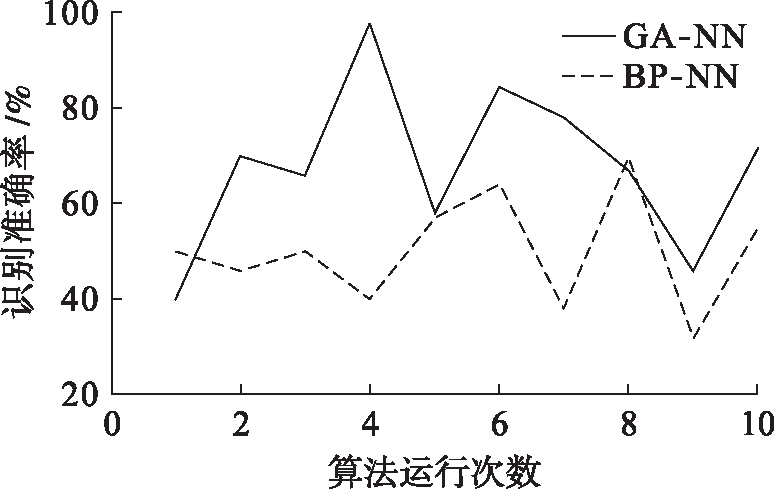
图6 两种算法的识别准确度比较
Fig.6 Comparison in recognition accuracy between two algorithms
为进一步比较本文算法与BP神经网络间的差异性，使用有功功率和无功功率作为神经网络的输入，此时测试结果如图7所示.从图7中可以看出，引入2种特征后，两种算法的性能均有明显的提升，且基于遗传算法优化的神经网络的性能更加稳定.
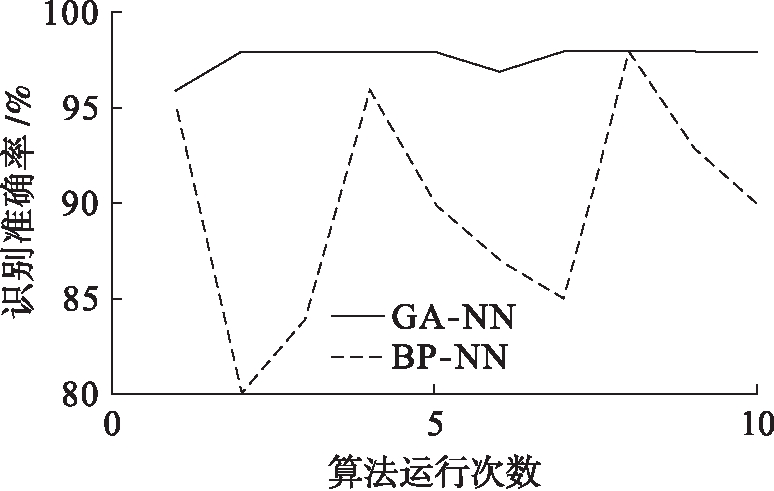
图7 使用2种特征时两种算法识别精度比较
Fig.7 Comparison in recognition accuracy between two algorithms with two characteristics
为了排除不同特征组合对算法性能的影响，本文比较了加入非活性电流谐波特征前、后两种算法的识别准确率，结果如图8所示.GA-NN和BP-NN为未加入非活性电流谐波特征的结果；GA-NN+N-Har和BP-NN+N-Har为加入非活性电流谐波特征后的结果.从图8可以看出，两种算法的准确率在经过一定的迭代后均趋于稳定，且使用非活性电流谐波特征能明显提高两种算法的识别精度.这表明非活性电流谐波特征能增强不同电器的区分度，增强电器负荷识别效果.从图8还可以看出，本文提出的遗传算法优化神经网络识别率明显高于传统的BP算法.使用相同的算法时，包含非活性电流谐波特征的算法能获得更高的精度.
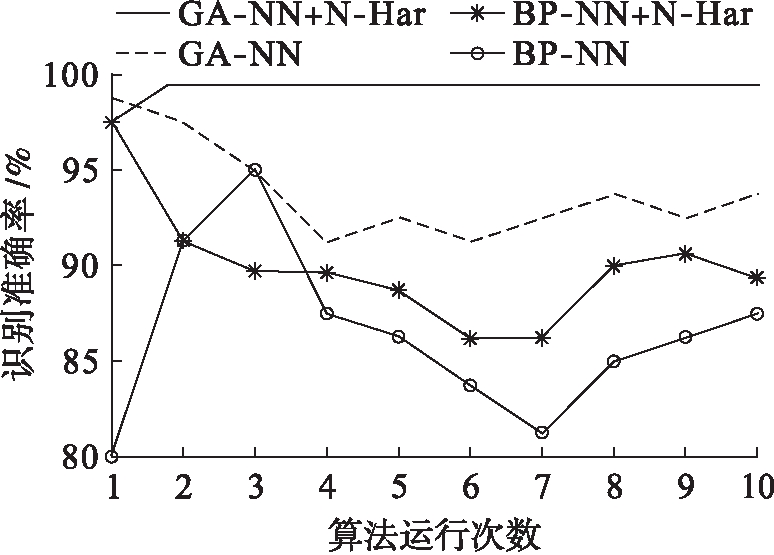
图8 使用不同特征组合时算法性能比较
Fig.8 Comparison in algorithm performance with different characteristic combinations
本文提出了一种基于谐波特征和遗传算法的非侵入式电器负荷识别算法，它采用遗传算法优化的神经网络模型来实现粒度用电分析，相比传统的神经网络，所提出的算法能获得更高的负荷识别精度及更快的识别速度.仿真与测试结果表明了该算法的有效性.
[1] Li Q S，Xiao Y，Peng L I，et al.Research on harmonic characteristics of electric devices for non-intrusive load monitoring [J].Southern Power System Technology，2016，7：58-65.
[2] Vann J M，Karnowski T P，Kerekes R，et al.A dimensionally aligned signal projection for classification of unintended radiated emissions [J].IEEE Transactions on Electromagnetic Compatibility，2018，99：1-10.
[3] 张燕，谢峰.基于改进RBF神经网络的电力负荷预测 [J].电子设计工程，2013，21(1)：117-118.
(ZHANG Yan，XIE Feng.Electric load forecasting based on improved RBF neural network [J].Electro-nic Design Engineering，2013，21(1)：117-118.)
[4] 李媛，武岩岩，王思琪.基于混沌时间序列的Elman神经网络工业用电预测 [J].沈阳工业大学学报，2016，38(2)：196-200.
(LI Yuan，WU Yan-yan，WANG Si-qi.Elman neural network prediction of electricity industry based on chaotic time series [J].Journal of Shenyang University of Technology，2016，38(2)：196-200.)
[5] 罗枚.基于MRA+LMBP模型对电力系统短期负荷预测的研究 [J].现代电子技术，2007，30(18)：114-116.
(LUO Mei.Study on short-term load forecasting of power system based on MRA+LMBP model [J].Modern Electronic Technology，2007，30(18)：114-116.)
[6] 马小慧，阳育德，龚利武.基于Kohonen聚类和SVM组合算法的电网日最大负荷预测 [J].电网与清洁能源，2014，30(2)：7-11.
(MA Xiao-hui，YANG Yu-de，GONG Li-wu.Daily maximum load forecasting of power grid based on Kohonen clustering and SVM combined algorithm [J].Power Grid and Clean Energy，2014，30(2)：7-11.)
[7] 祁兵，程媛，武昕.基于Fisher有监督判别的非侵入式居民负荷辨识方法 [J].电网技术，2016，40(8)：2484-2490.
(QI Bing，CHENG Yuan，WU Xin.Method of non intrusive resident load identification based on the Fisher supervised discrimination [J].Power Grid Techno-logy，2016，40(8)：2484-2490.)
[8] 时广献，李春辉，李宏博.基于联想神经网络算法的电力系统负荷预测 [J].电子科技，2010，23(12)：62-66.
(SHI Guang-xian，LI Chun-hui，LI Hong-bo.Power system load forecasting based on associative neural network algorithm [J].Electronic Science and Technology，2010，23(12)：62-66.)
[9] 陈鸿川，刘博，栾文鹏，等.用于非侵入式电力负荷监测的改进Viterbi算法 [J].电力系统及其自动化学报，2017，29(2)：84-88.
(CHEN Hong-chuan，LIU Bo，LUAN Wen-peng，et al.Improved Viterbi algorithm for non-invasive power load monitoring [J].Power System and Automation Journal，2017，29(2)：84-88.)
[10] 姜波.基于深度学习的非侵入式住宅用电负荷分解方法 [D].合肥：合肥工业大学，2017.
(JIANG Bo.Non intrusive residential electrical load decomposition method based on deep learning [D].Hefei：Hefei University of Technology，2017.)
[11] 汪四仙，毕忠勤.非侵入式电力负荷监测技术研究 [J].上海电力学院学报，2017(4)：357-361.
(WANG Si-xian，BI Zhong-qin.Research on non intrusive power load monitoring technology [J].Journal of Shanghai University of Electric Power，2017(4)：357-361.)
[12] 武昕，祁兵，韩璐，等.基于模板滤波的居民负荷非侵入式快速辨识算法 [J].电力系统自动化，2017，41(2)：135-141.
(WU Xin，QI Bing，HAN Lu，et al.Non intrusive fast identification algorithm of resident load based on template filtering [J].Power System Automation，2017，41(2)：135-141.)
[13] 祁兵，韩璐.基于遗传优化的非侵入式居民负荷辨识算法 [J].电测与仪表，2017，54(17)：11-17.
(QI Bing，HAN Lu.Non invasive resident load identification algorithm based on genetic optimization [J].Electrical Measurement and Instrumentation，2017，54(17)：11-17.)
[14] Welikala S，Dinesh C，Ekanayake M P B，et al.Incorporating appliance usage patterns for non-intrusive load monitoring and load forecasting [J].IEEE Tran-sactions on Smart Grid，2017(99)：1-19.