建筑物可持续和人与自然生态共存的理念正促使建筑材料向绿色、环保方向发展,而不锈钢材料因具有超强的耐腐蚀性、耐久性、耐火性和易维护等特性使其越来越多地应用于建筑工程[1-2].
Kim等[3-4]认为不锈钢螺栓连接的承压性能可根据变形准则和强度准则两种方法来确定.通过试验和有限元模拟对两螺栓和四螺栓连接进行参数研究,提出承压强度折减率与板厚的关系,得到在翘曲影响下修正的单个螺栓连接节点承压承载力公式.Cai等[5]对高温下单剪螺栓连接节点进行研究,发现单剪螺栓连接主要有净截面和承压失效两种破坏模式,且发达国家规范中单剪螺栓连接的强度取值是偏保守的.关建[6]对不锈钢螺栓连接节点进行承压性能分析,考虑了端距、螺栓直径和板厚等影响因素,并提出两种承压强度公式.以上这些研究主要集中在大六角头不锈钢螺栓连接抗剪承载力的研究,而关于内六角不锈钢螺栓连接抗剪承载力的研究鲜有报道.
为了解不锈钢内六角螺栓连接节点承压承载力的性能,考虑不同端距、边距及中心距设计3组10个试件进行抗剪性能试验.采用ABAQUS软件对试验进行有限元模拟分析,验证数值模拟的可行性.之后在可行性的基础上对不同端距和边距的42个内六角螺栓抗剪连接节点进行分析,参照Kim提出的破坏模式及判断标准来确定连接节点承压承载力.
试验板件采用奥氏体30408不锈钢材料,相应的中国牌号为06Cr19Ni10.螺栓为正国标304不锈钢内六角螺丝圆柱头螺钉,组别A2,性能等级70.螺栓连接中考虑边距、端距和板件厚度等参数,试验中螺栓直径均为16 mm,螺栓孔径为17 mm.试验采用WAW-600KN微机控制电液伺服万能试验机加载,对各个试件进行加载得到各试件的位移![]() 荷载数据,以及相关各试件破坏模式等相关信息.
荷载数据,以及相关各试件破坏模式等相关信息.
1.2.1 材料模型
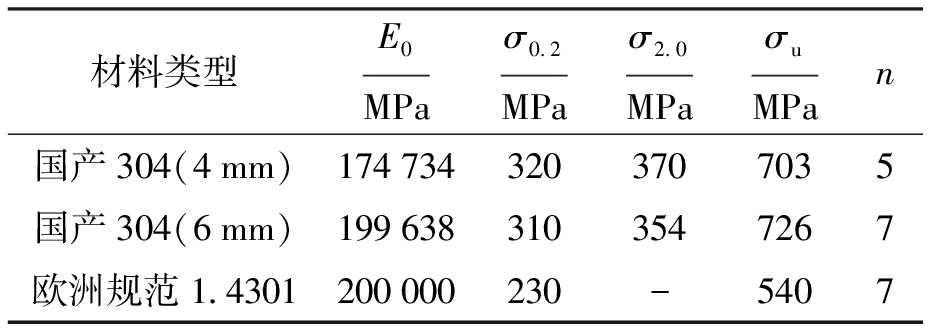
试验选用的国产304不锈钢材性数据[7]如表1所示.表1中,E0为弹性模量;σ0.2和σ2.0为残余应变0.2%和2.0%时对应的弹性极限应力值;n为应变硬化指数;σu为极限应力.通过将名义应力![]() 应变转换为真实应力
应变转换为真实应力![]() 应变并输入ABAQUS软件,本构模型中不考虑不锈钢材料的各向异性.
应变并输入ABAQUS软件,本构模型中不考虑不锈钢材料的各向异性.
表1 不锈钢材料的材性数据
Tab.1 Properties of stainless steel
材料类型E0MPaσ0.2MPaσ2.0MPaσuMPan国产304(4mm)1747343203707035国产304(6mm)1996383103547267欧洲规范1.4301200000230-5407
1.2.2 接触及螺栓预紧力
连接中涉及的接触均采用面面接触,法向接触定义为硬接触,切向接触选用库伦摩擦接触.由于采用的是非摩擦型螺栓,故在分析中不考虑螺栓的预紧力,但为确保螺帽和螺母与板件接触以便分析施加10 N的预紧力[8].
1.2.3 网格划分
C3D8R单元有沙漏控制,计算时间少,且位移结果较精确[8],故本文采用C3D8R单元进行模拟.有限元模拟中芯板厚度为6 mm,盖板厚度为4 mm,螺栓直径为16 mm,有限元建模取螺栓盖板连接的1/2分析,且在有限元模拟中简化螺栓,将螺帽、螺母和螺杆都看作圆柱体,网格在应力集中处细化,模型如图1所示.
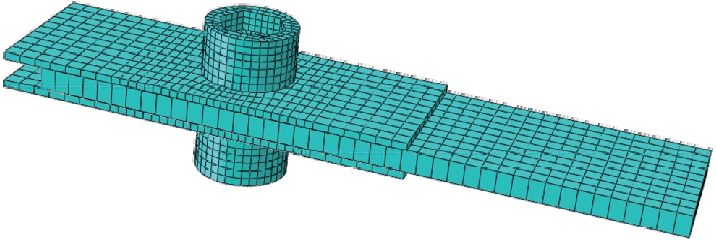
图1 不锈钢螺栓抗剪连接有限元1/2模型
Fig.1 Finite element 1/2 model for shear-resistant connection of stainless steel bolt
1.2.4 分析方法
由于有限元分析中涉及材料非线性和接触非线性,故采用位移加载,并在分析步里将初始增量调小到0.01,最大增量步设置为1 000,非线性分析开关调成ON,计算方法采用Newton-Raphson法求解,迭代次数设为25.
采用有限元分析方法对T1试件进行有限元分析,将T1试件的试验和有限元模拟得到的荷载![]() 位移曲线进行对比,结果如图2所示.
位移曲线进行对比,结果如图2所示.
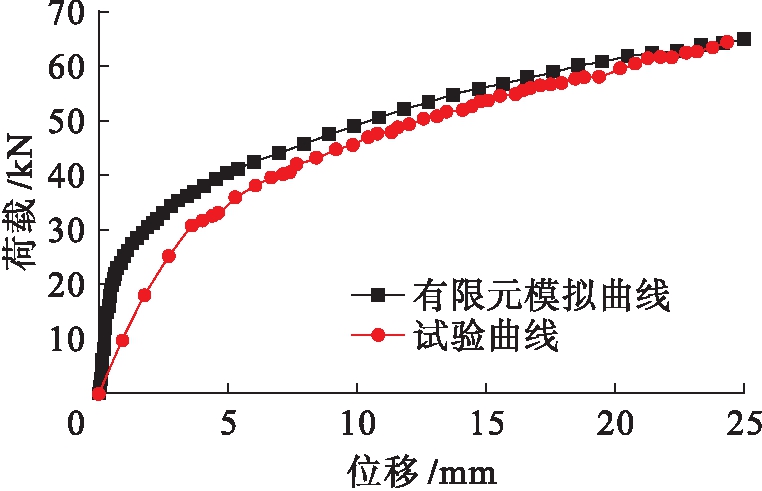
图2 有限元与试验荷载![]() 位移曲线
位移曲线
Fig.2 Load-displacement curves for finite element and test
由图2可知,加载初期试验值明显小于有限元分析值,但加载中期有限元的荷载值与试验值越来越接近,后期两者数值基本吻合.造成两者初期差异较大的原因为:
1) 有限元模拟中忽略螺纹影响,这加快了螺栓接触螺孔的速度,使有限元曲线在前期增长较快;
2) 试验试件有偏心,而有限元分析中则是完全对称的;
3) 试验加载初期连接板件和夹具之间有少许空隙,而有限元中是直接接触的.
考虑到结构正常使用下的要求,实际情况中以变形准则为参考,Kim等人的研究结果显示,当螺栓孔变形达到螺孔直径的30%时,螺栓连接节点已经不适合再继续承载,有限元模拟中螺栓直径为16 mm,螺孔尺寸为17 mm,螺孔变形量为5.1 mm即判定构件达到破坏状态.因此,在有限元模拟中通过对荷载![]() 螺孔变形的测量来判断承压承载力.
螺孔变形的测量来判断承压承载力.
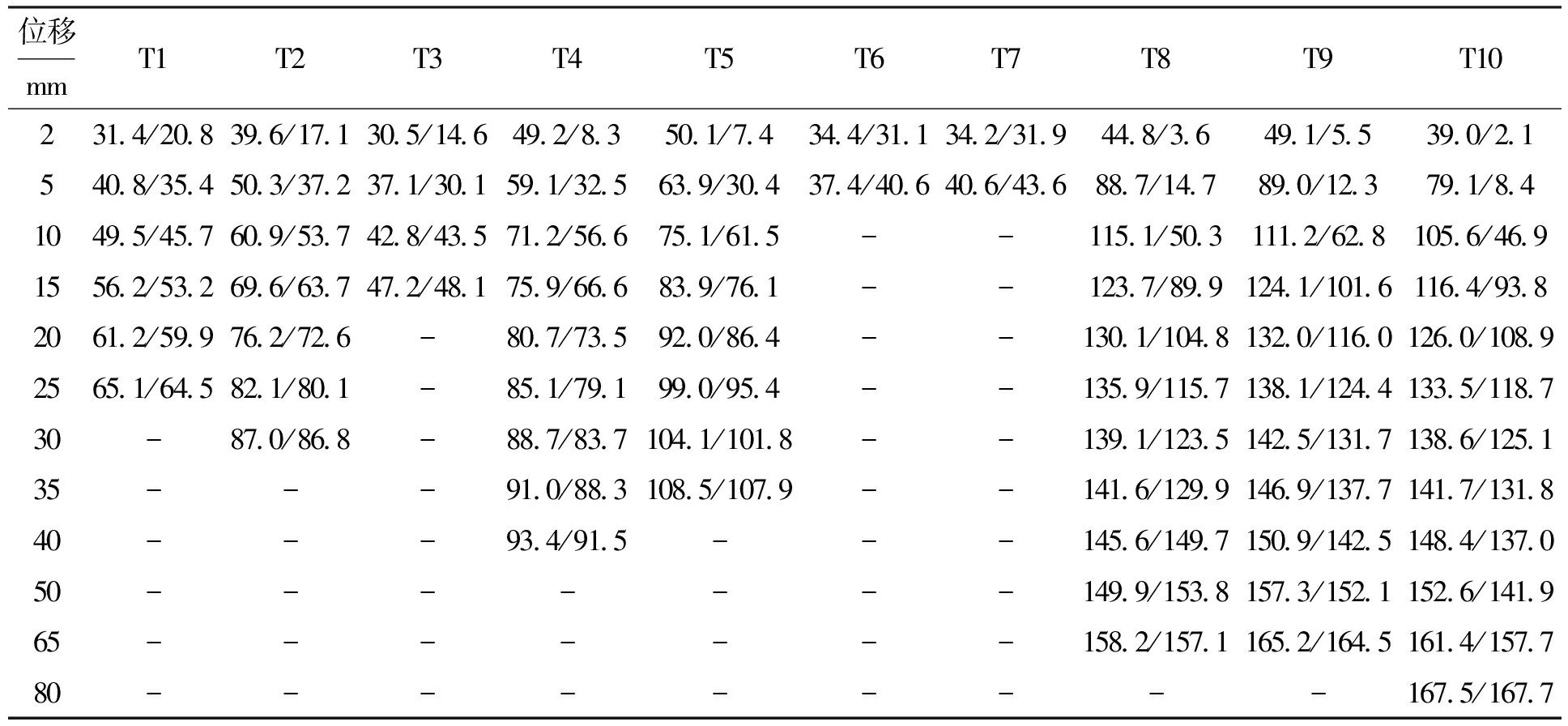
表2给出了试验和有限元模拟不同位移下各试件的受力情况对比,可见两者在加载初期差值加大,中后期越来越接近.事实上,当螺孔变形量达到5.1 mm时,试件加载已到中后期,此时有限元分析能较好地模拟螺栓连接节点的真实受力状态,故采用有限元模拟分析不锈钢螺栓连接节点承压性能可靠性较高.
表2 不同位移下试验和有限元模拟对应的承压承载力
Tab.2 Corresponding bearing capacity under compression for test and finite element simulation under different displacement kN
位移mmT1T2T3T4T5T6T7T8T9T10231.4/20.839.6/17.130.5/14.649.2/8.350.1/7.434.4/31.134.2/31.944.8/3.649.1/5.539.0/2.1540.8/35.450.3/37.237.1/30.159.1/32.563.9/30.437.4/40.640.6/43.688.7/14.789.0/12.379.1/8.41049.5/45.760.9/53.742.8/43.571.2/56.675.1/61.5--115.1/50.3111.2/62.8105.6/46.91556.2/53.269.6/63.747.2/48.175.9/66.683.9/76.1--123.7/89.9124.1/101.6116.4/93.82061.2/59.976.2/72.6-80.7/73.592.0/86.4--130.1/104.8132.0/116.0126.0/108.92565.1/64.582.1/80.1-85.1/79.199.0/95.4--135.9/115.7138.1/124.4133.5/118.730-87.0/86.8-88.7/83.7104.1/101.8--139.1/123.5142.5/131.7138.6/125.135---91.0/88.3108.5/107.9--141.6/129.9146.9/137.7141.7/131.840---93.4/91.5---145.6/149.7150.9/142.5148.4/137.050-------149.9/153.8157.3/152.1152.6/141.965-------158.2/157.1165.2/164.5161.4/157.780---------167.5/167.7
为了研究承压承载力与端距比e1/d和边距比e2/d的关系.考虑不同端距比(1.0、1.5、2.0、2.5、3.0、3.5和4.0)、边距比(1.5、2.0、2.5、3.0、3.5和4.0)设计42个试件进行有限元分析.
采用前文提到的变形准则来判断不锈钢螺栓连接节点的承压承载力,通过有限元模拟分析得到42个试件在螺栓孔处变形为5.1 mm时对应的承压承载力,具体有限元分析得到的数据如表3所示.端距比和边距比两者的相互影响关系如图3、4所示.
由图3、4可知:
1) 当e2=1.5d且e1≤2.5d时,随着端距比增大,承载力显著加大;而e1≥2.5d时,端距比对承压承载力影响较小.在e2=1.5d时,不同端距比下板件孔洞处的净截面面积较小,破坏形态如图5所示,表现为净截面破坏.
表3 不同e1/d和e2/d下对应位移的承压承载力
Tab.3 Bearing capacity under compression of corresponding displacement at different e1/d and e2/d kN
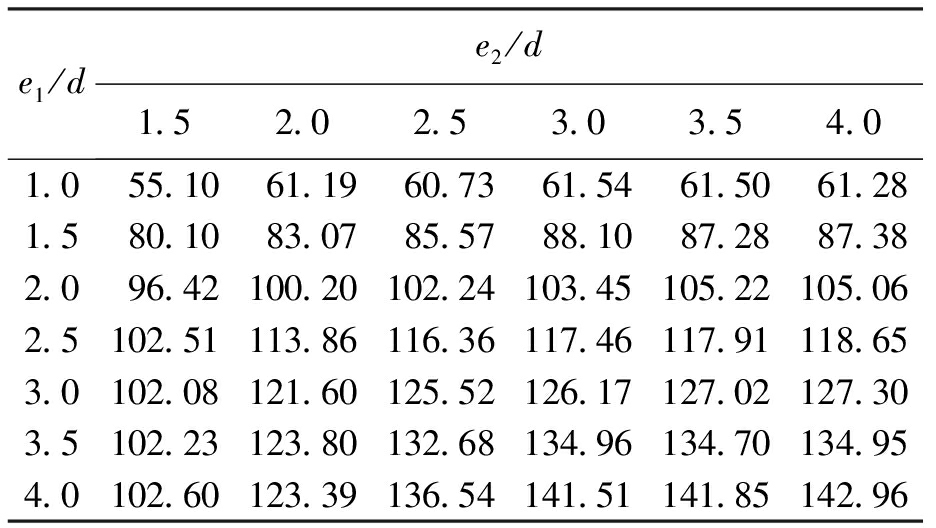
e1/de2/d1.52.02.53.03.54.01.055.1061.1960.7361.5461.5061.281.580.1083.0785.5788.1087.2887.382.096.42100.20102.24103.45105.22105.062.5102.51113.86116.36117.46117.91118.653.0102.08121.60125.52126.17127.02127.303.5102.23123.80132.68134.96134.70134.954.0102.60123.39136.54141.51141.85142.96
2) 端距比一定且e2≥3d时,端距比对承压承载力影响较小;当e2≤1.5d时,边距比的变化对承压承载力的影响较小,连接破坏表现为冲切破坏,如图6所示.
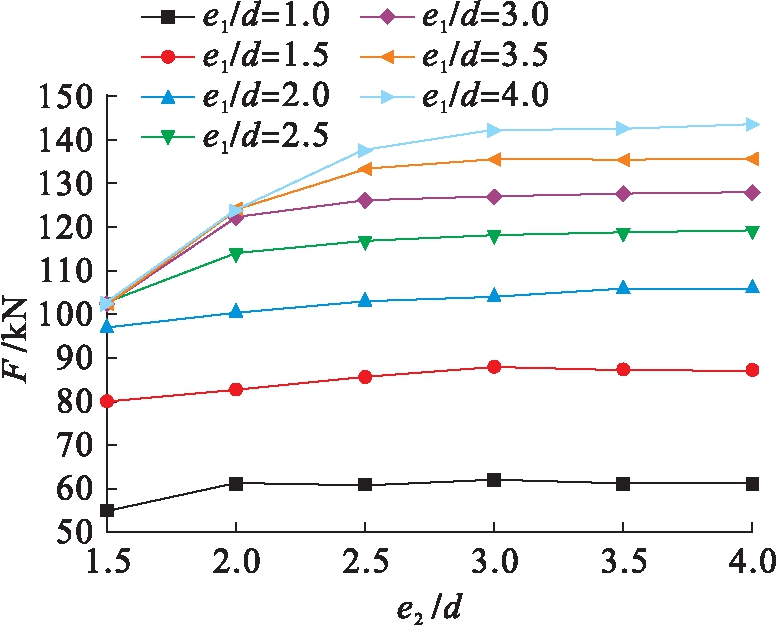
图3 不同端距比下荷载![]() 边距比曲线
边距比曲线
Fig.3 Load-edge distance ratio curves under different end distance ratio
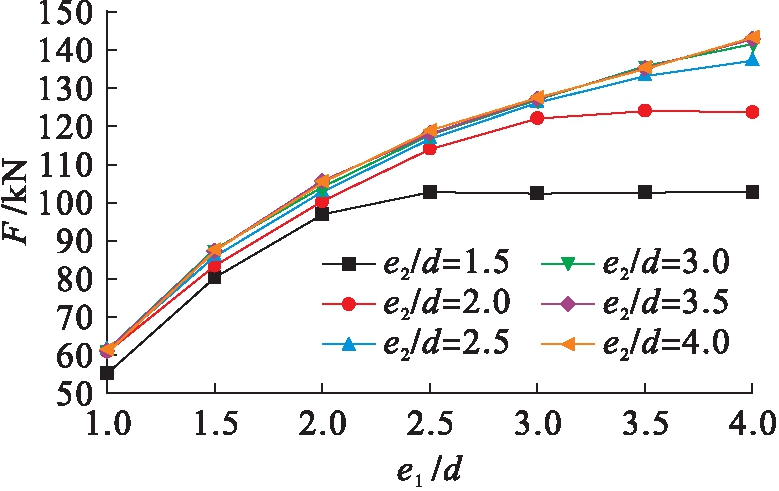
图4 不同边距比下荷载![]() 端距比曲线
端距比曲线
Fig.4 Load-end distance ratio curves under different edge distance ratio
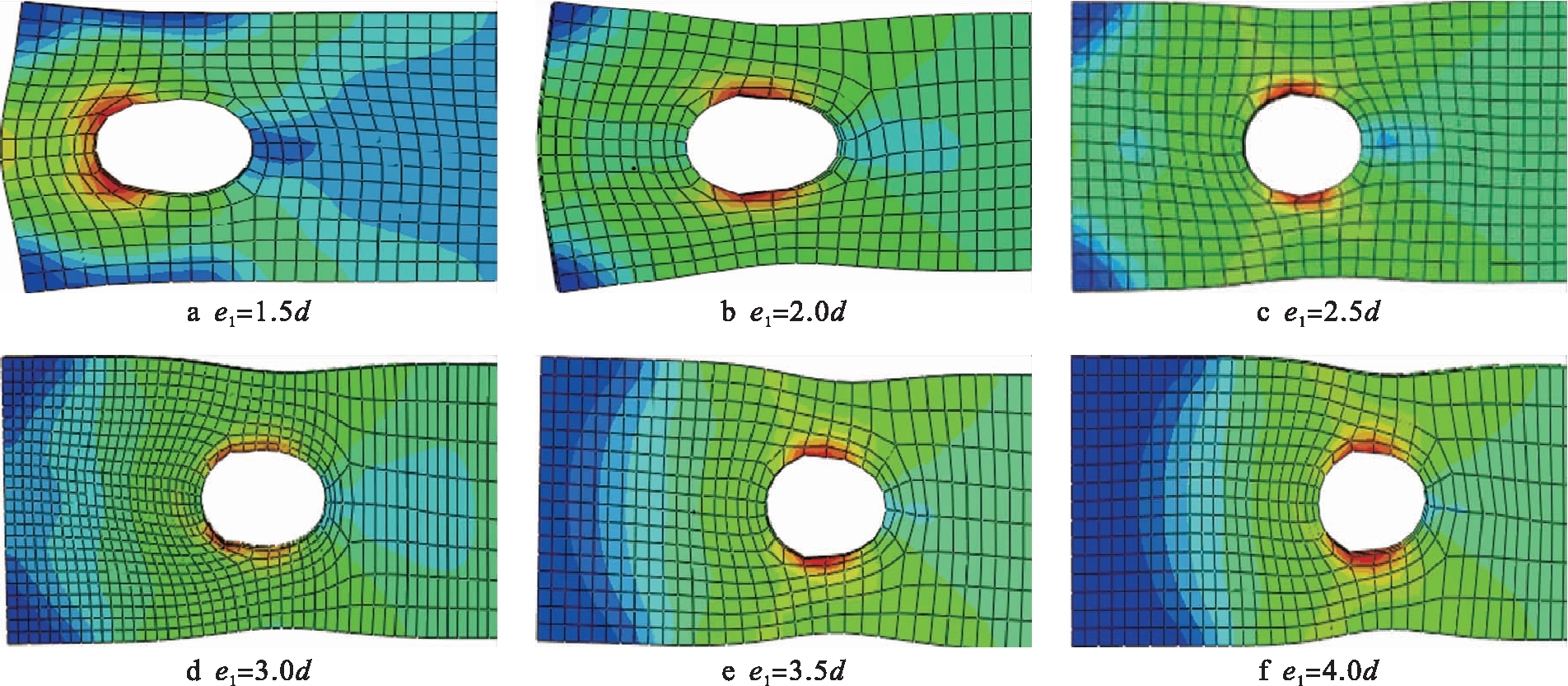
图5 当e2=1.5d时不同e1/d下的板件达到承压荷载时的破坏形态
Fig.5 Failure morphologies of plates reaching pressure bearing load at different e1/d with e2=1.5d
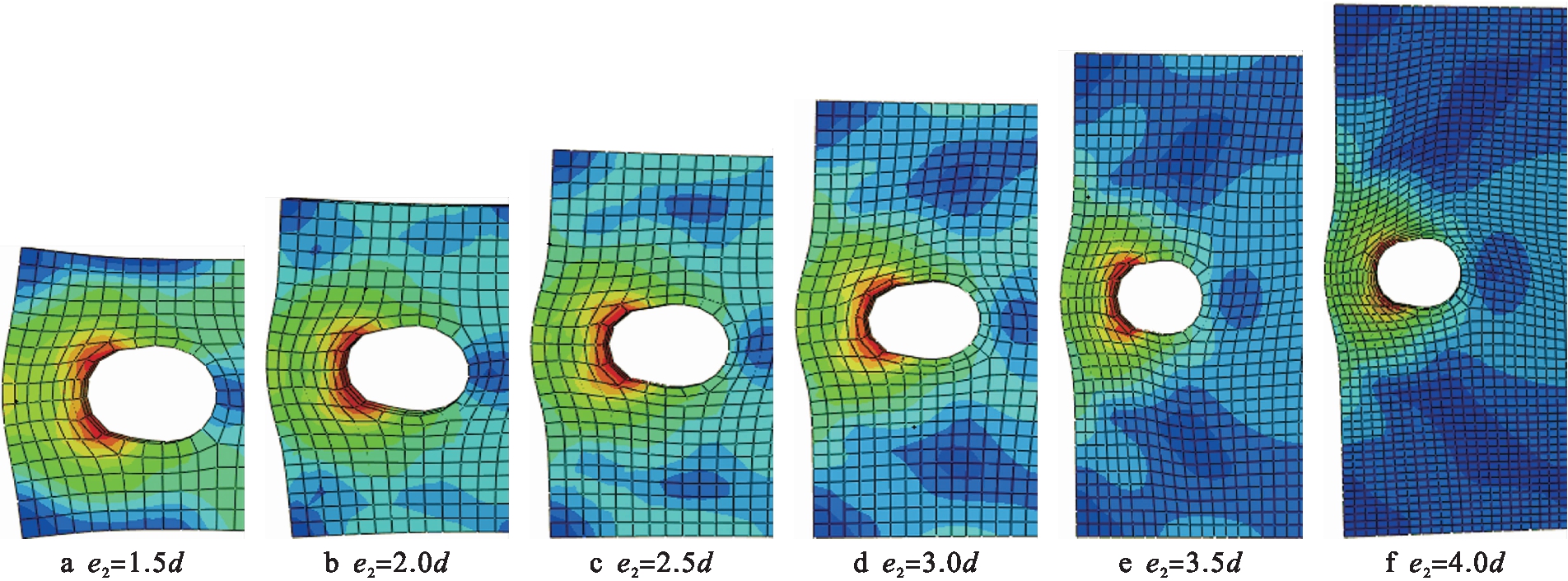
图6 当e1=1.5d时不同e2/d下的板件达到承压荷载时的破坏形态
Fig.6 Failure morphologies of plates reaching pressure bearing load at different e2/d with e1=1.5d
在本文中,不锈钢材料的极限抗拉强度用fu表示.考虑承压承载力随端距比e1/d和边距比e2/d的变化规律时,将取值范围选为1.5d≤e1≤4d,2d≤e2≤3d,提出不锈钢材料承压承载力的建议公式为
F=fudt·g(e1/d,e2/d)/γ
(1)
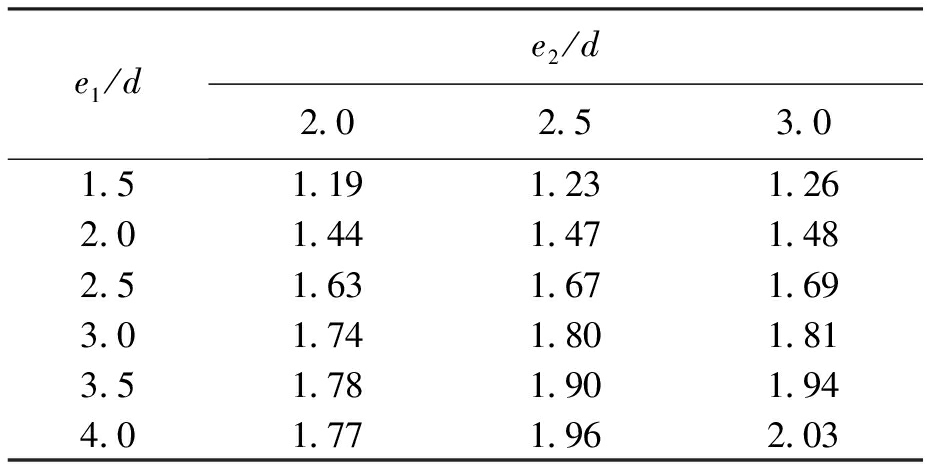
式中:F为承压承载力;fu为板件抗拉强度;d为螺栓直径;t为不锈钢板厚度;g(e1/d,e2/d)为一个关于e1/d和e2/d的函数;γ为抗力系数.fu·g(e1/d,e2/d)可定义为板件承压强度,用fc表示,为了得到函数g(e1/d,e2/d),将表3中计算所得的承压荷载值,在1.5d≤e1≤4d、2d≤e2≤3d范围内,按照式(1)转换求得不同e1/d和e2/d下的g(e1/d,e2/d)函数值,结果如表4所示.假设该函数g(e1/d,e2/d)=a0+a1(e1/d)+a2(e2/d)+a3(e1/d)(e2/d),通过MATLAB软件中rstool中的interaction功能函数,可确定各参数分别为a0=1.141 7,a1=0.086 7,a2=-0.097 4,a3=0.075 4,均方根误差为0.075 1.
表4 不同e1/d和e2/d下的g(e1/d,e2/d)值
Tab.4 Values of g(e1/d,e2/d)at different e1/d and e2/d
e1/de2/d2.02.53.01.51.191.231.262.01.441.471.482.51.631.671.693.01.741.801.813.51.781.901.944.01.771.962.03
函数可表示为
g(e1/d,e2/d)= 1.14+0.09(e1/d)-0.10(e2/d)+
0.08(e1/d)(e2/d)
(2)
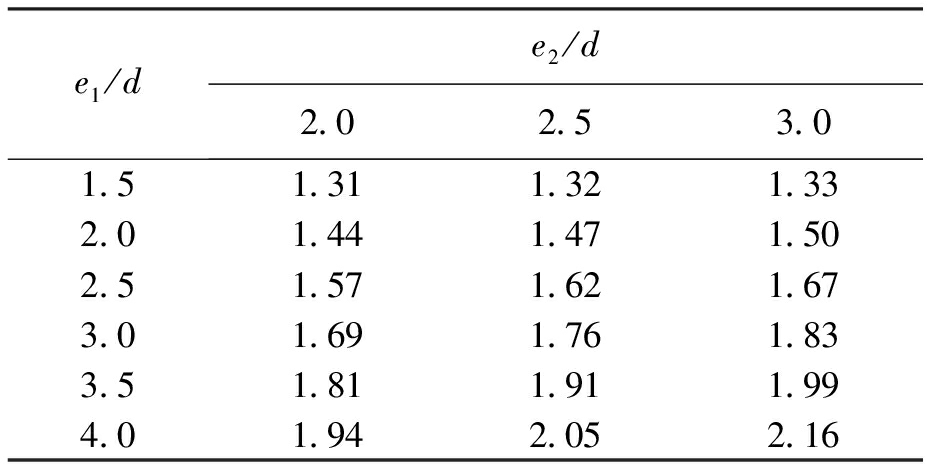
公式模拟的结果如表5所示,对比表4可以看出公式(2)的模拟效果较好.
表5 建议公式(2)模拟结果
Tab.5 Simulation results of suggested formula (2)
e1/de2/d2.02.53.01.51.311.321.332.01.441.471.502.51.571.621.673.01.691.761.833.51.811.911.994.01.942.052.16
为了能直观地看到端距比对承压强度的影响,只考虑e1/d变化,将e2/d固定,假设
F=fudt·h(e1/d)/γ
(3)
对e2≥2d时的试验数据进行模拟,分别得到不同e2/d下h(e1/d)的线性函数表达式.
当e2=2d,1.5d≤e1≤4d时,则有
h(e1/d)=0.23(e1/d)+0.96
当e2=2.5d,1.5d≤e1≤4d时,则有
h(e1/d)=0.29(e1/d)+0.87
当e2=3d,1.5d≤e1≤4d时,则有
h(e1/d)=0.31(e1/d)+0.86
结合有限元计算结果和上述函数表达式的关系,将结果简化得到承压强度计算公式,即
fc=fu(0.28(e1/d)+0.90)
(4)
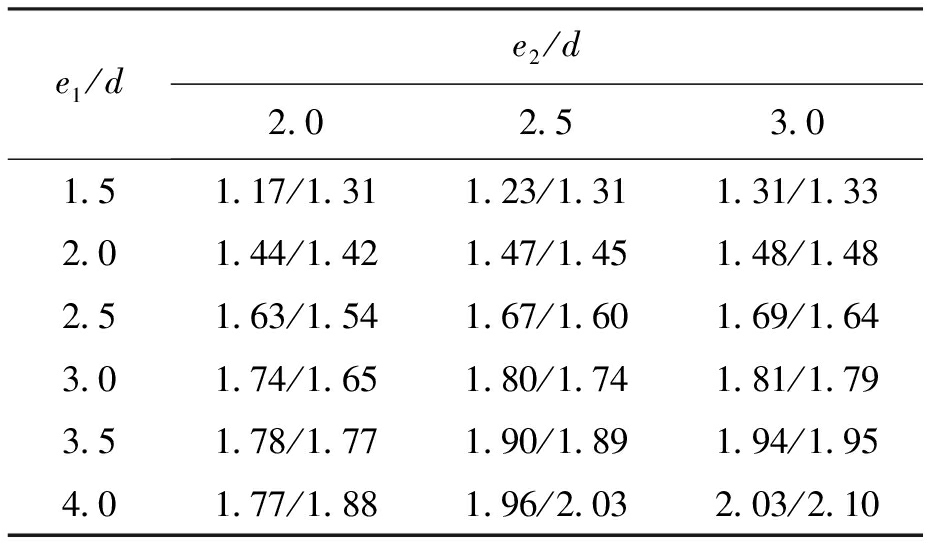
式(4)的适用范围为2d≤e2≤3d,1.5d≤e1≤4d,当e2≥3d时取e2=3d,当e1≥4d时取e1=4d.将式(4)的模拟结果与有限元计算结果进行对比,结果如表6所示.从表6中可以看出,式(4)能较好地模拟有限元计算结果,表6中数据前为建议公式值,后为有限元计算值.
表6 建议公式(4)计算值与有限元计算值的对比
Tab.6 Comparison between calculated values of suggested formula (4)and calculated values of finite element
e1/de2/d2.02.53.01.51.17/1.311.23/1.311.31/1.332.01.44/1.421.47/1.451.48/1.482.51.63/1.541.67/1.601.69/1.643.01.74/1.651.80/1.741.81/1.793.51.78/1.771.90/1.891.94/1.954.01.77/1.881.96/2.032.03/2.10
欧洲规范(BS EN 1993-1-8)[9]中承压承载力的计算公式为
Fb,Rd=k1αbfu,reddt0/γM2
(5)
式中:Fb,Rd为承压承载力;fu,red为抗拉极限折减强度,fu,red=0.5fy+0.6fu,fy为连接板件的抗拉屈服强度;γM2为安全系数,取1.25;k1、αb分别为螺栓位置相关系数和荷载传递方向系数;t0为连接受力方向较薄部分的板件厚度.
将式(3)、(4)与式(5)的计算结果进行对比,其中,抗力系数γ=γM2取1.25,为方便提出的公式应用于实际中,式(3)、(4)的材性数据采用《不锈钢结构技术规程》[10]中的材性数据fu=515 MPa;式(5)采用欧洲规范材性数据,其中fu=540 MPa,fy=230 MPa,之后可得到fu,red=0.5fy+0.6fu=439 MPa,计算结果对比如表7所示.
从表7中可以看出,欧洲规范在e1/d=1.5时相对建议值较保守,在e1/d=2.0时,两者吻合情况达到最好,在e1/d=2.5时,两者差值又增大,在3≤e1/d≤4之间,欧洲规范计算值与建议公式的差值在减少.总体来说,建议公式与欧洲规范公式计算值结果吻合较好,建议提出的两种承载力公式可应用于实际工程中.
表7 建议公式与BS EN 1993-1-8对比
Tab.7 Comparison between suggested formula and BS EN 1993-1-8 kN
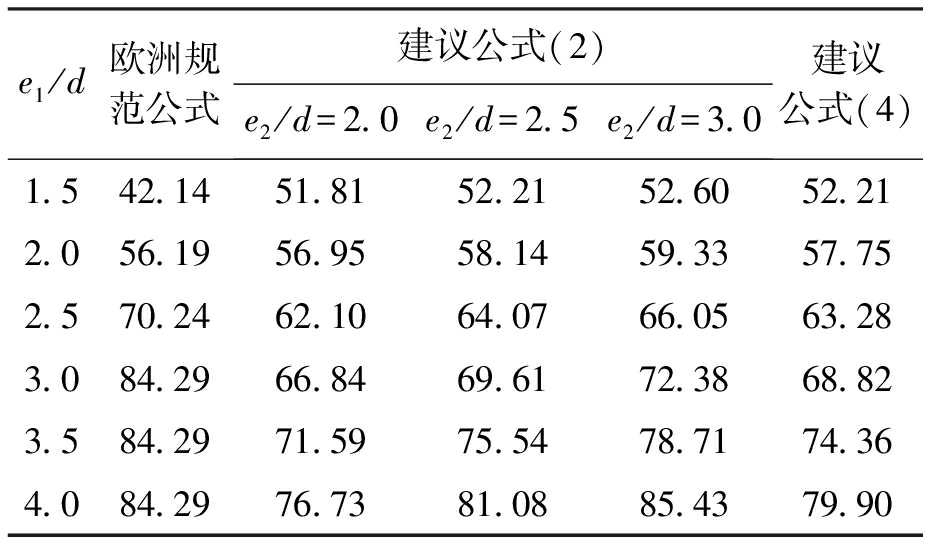
e1/d欧洲规范公式建议公式(2)e2/d=2.0e2/d=2.5e2/d=3.0建议公式(4)1.542.1451.8152.2152.6052.212.056.1956.9558.1459.3357.752.570.2462.1064.0766.0563.283.084.2966.8469.6172.3868.823.584.2971.5975.5478.7174.364.084.2976.7381.0885.4379.90
本文在欧洲规范BS EN 1993-1-8和不锈钢材性试验分析的基础上,应用ABAQUS有限元软件计算分析了42组模型,之后提出两种承压承载力的设计公式.
第一个公式为fc=fu·g(e1/d,e2/d),其中,g(e1/d,e2/d)=1.14+0.09(e1/d)-0.10(e2/d)+0.08(e1/d)(e2/d),该公式参数的适用范围为1.5d≤e1≤4d,2d≤e2≤3d;当e1≥4d时取e1=4d,当e2≥3d时取e2=3d.
第二个公式为fc=fu(0.28(e1/d)+0.90),该公式适用范围为1.5d≤e1≤4d,2d≤e2≤3d;当e1≥4d时取e1=4d,当e2≥3d时取e2=3d.
计算对比建议公式与欧洲规范下的承压承载力,发现在1.5≤e1/d≤4之间,随着e1/d增大,建议公式与欧洲规范公式计算差值先减小后增大再减小,但总体上计算结果与欧洲规范较接近.
[1] Kim T S,Kuwamura H.Finite element modeling of bolted connections in thin-walled stainless steel plates under static shear [J].Thin-Walled Structures,2007,45(4):407-421.
[2] 李德元,娄建新,孔令伟,等.12Cr1MoV/304不锈钢焊接接头高温时效碳迁移现象 [J].沈阳工业大学学报,2015,37(1):28-33.
(LI De-yuan,LOU Jian-xin,KONG Ling-wei,et al.Carbon migration phenomenon in high temperature aging process of 12CrlMoV/304 welding joint [J].Journal of Shenyang University of Technology,2015,37(1):28-33.)
[3] Kim T S,Lim J S.Ultimate strength of single shear two-bolted connections with austenitic stainless steel [J].International Journal of Steel Structures,2013,13(1):117-128.
[4] Lim J S,Kim T S,Kim S H.Ultimate strength of single shear bolted connections with cold-formed ferritic stainless steel [J].Journal of Zhejiang University-Science A(Applied Physics & Engineering),2013,14(2):120-136.
[5] Cai Y,Young B.Behavior of cold-formed stainless steel single shear bolted connections at elevated temperatures [J].Thin-Walled Structures,2014,75(2):63-75.
[6] 关建.不锈钢构件螺栓连接节点及焊接工形截面残余应力研究[D].北京:北京交通大学,2012.
(GUAN Jian.Research on bolted connection and residual stress in fabricated I-section in structural stainless steel[D].Beijing:Beijing Jiaotong University,2012.)
[7] 邓泽鹏.不锈钢螺栓连接节点抗剪性能研究[D].长春:吉林建筑大学,2016.
(DENG Ze-peng.Study on the performance of joint shear stainless steel bolt connection[D].Changchun:Jilin Jianzhu University,2016.)
[8] 冷捷,刘文渊,段文峰.不锈钢普通螺栓抗剪连接破坏模式的数值研究 [J].吉林建筑工程学院学报,2014,31(5):15-18.
(LENG Jie,LIU Wen-yuan,DUAN Wen-feng.Numerical investigation of mode fractures in stainless steel bolted shear connection [J].Journal of Jilin Institute of Architecture & Civil Engineering,2014,31(5):15-18.)
[9] British Standard Institution.BS EN 1993-1-8 Eurocode 3:design of steel structures:part 1-8:design of joints [S].London:British Standard Institution,2005.
[10] 中国工程建设标准化协会.CECS 410:2015不锈钢结构技术规程 [S].北京:中国计划出版社,2015.
(China Association for Engineering Construction Standardization.CECS 410:2015 Technical specification for stainless steel structure [S].Beijing:China Planning Press,2015.)