应变曲线，分析了割线模量峰值与弹塑性变形的相关性.结果表明，在应力应变全过程中割线模量存在明显峰值，且达到峰值后呈现衰减特征.峰值所在的位置与其弹性极限具有较为稳定的对应关系，因而通过确定该峰值所在位置可以间接确定弹性极限.割线模量峰值与弹性极限均可能受到加载速度、边界条件或应力状态等因素的影响，还可能存在尺寸或形状效应.摘 要：为了快速确定金属材料单轴应力状态下的弹性极限或屈服应力，对高碳钢与低碳钢进行了拉伸和压缩试验，绘制了割线模量应变曲线，分析了割线模量峰值与弹塑性变形的相关性.结果表明，在应力应变全过程中割线模量存在明显峰值，且达到峰值后呈现衰减特征.峰值所在的位置与其弹性极限具有较为稳定的对应关系，因而通过确定该峰值所在位置可以间接确定弹性极限.割线模量峰值与弹性极限均可能受到加载速度、边界条件或应力状态等因素的影响，还可能存在尺寸或形状效应.
在制造业领域弹性极限是保证仪表用弹性合金正常工作的基本指标，准确测量材料的弹性极限是弹性元器件设计和材料合理使用的基础.在工程建设领域弹性极限也是保证构件或结构正常工作的基础.不同工况下的弹性极限以及屈服应力的理论分析与试验研究已经成为传统热点问题[1-3].在轴向拉伸或压缩试验中，随着应力的增加，材料内部自身结构会发生变化，随之出现了比例极限、弹性极限、屈服极限、强度极限等，而其中前3个强度特征值都可以表征金属发生微小塑性变形时所对应的抗力，很难进行严格区别，尤其是弹性极限和屈服极限，两者并无本质区别，只是对应的塑性变形大小略有差异[4]，这导致准确界定弹性极限只存在理论意义，换言之得到的数值仅为近似弹性极限.
通过绘制金属材料割线模量应变曲线后发现，割线模量峰值与其弹性极限关联度较高，这里的弹性极限与GB/T 228.1-2010中的上屈服强度在数值上较为接近.若割线模量峰值与弹性极限具有较为固定的对应关系，则表明割线模量峰值也会与上屈服强度具有确定的对应关系，因而割线模量峰值可用于判定材料受力时的弹塑性转化情况.
将割线模量与材料强度和变形联系起来的情况常见于土力学中.文献[5]采用割线模量法分析了土体变形偏小的原因；文献[6]通过普通水泥混凝土的压缩试验，计算了不同应力和应变水平下的割线模量，给出了混凝土弹性模量的近似取值方法；文献[7]研究了应力路径对饱和软黏土割线模量的影响.在土力学领域更多地将割线模量用于评定岩土材料强度和变形特性[8-10].在实际工程结构中，通过监测构件的割线模量发展演化，可以判定构件在荷载作用下的响应程度.为此，本文开展了高碳钢和低碳钢的轴向拉伸和压缩试验，绘制了割线模量应变曲线，探讨了割线模量峰值与弹性极限的相关性.
应变曲线图1为割线模量及割线模量应变曲线.由图1a可见，某点的割线模量在数值上为应力应变曲线上该点纵坐标与横坐标的比值，将该点的应力与应变相除，即可得到该点处的割线模量，其表达式为
Ec=tanα=Δσ/Δε
(1)
将应力应变曲线上所有点的应力与对应的应变相除，即可得到所有点对应的割线模量.若以割线模量为纵坐标，对应的应变为横坐标，即可得割线模量应变曲线，结果如图1b所示.
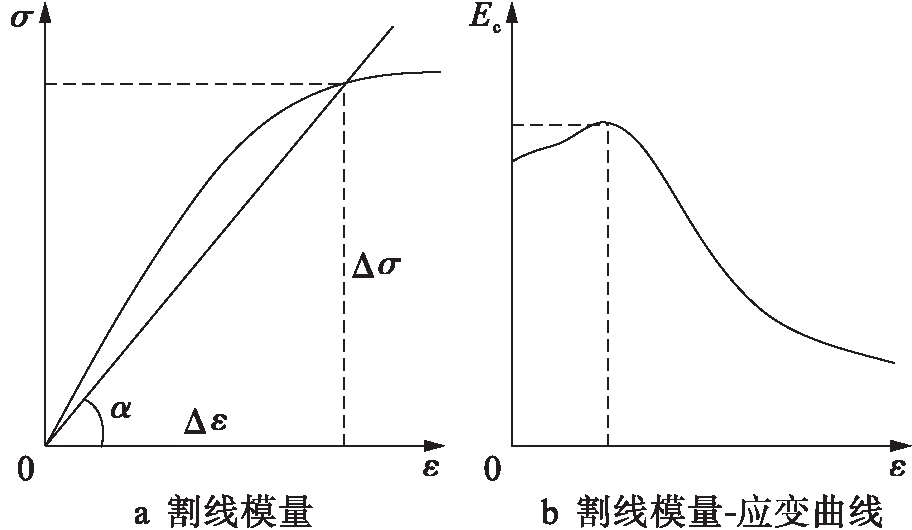
图1 割线模量及割线模量应变曲线
Fig.1 Secant modulus and secant modulus-strain curve
本文压缩试验采用直径为15 mm、长度为30 mm的圆柱试件，拉伸试验采用直径为10 mm、标距为100 mm的圆柱试件.采用位移控制模式进行加载，本文试验中加载速度为0.5 mm/min，在此加载速度下产生的应力速率符合GB/T 228.1-2010要求.试验温度为常温，符合GB/T 228.1-2010中试验温度为10～35 ℃的要求[11].
应变曲线和割线模量应变曲线试验完毕后，将系统自动采集的应力、应变数据进行换算，并根据割线模量定义与本文给出的割线模量应变曲线绘制方法，将高碳钢和低碳钢的轴向拉伸和压缩试验数据进行换算，得到相应的割线模量应变曲线.为了对比割线模量与应力的增减关系，在同一幅图中一并给出应力应变曲线与割线模量应变曲线，结果如图2～5所示.
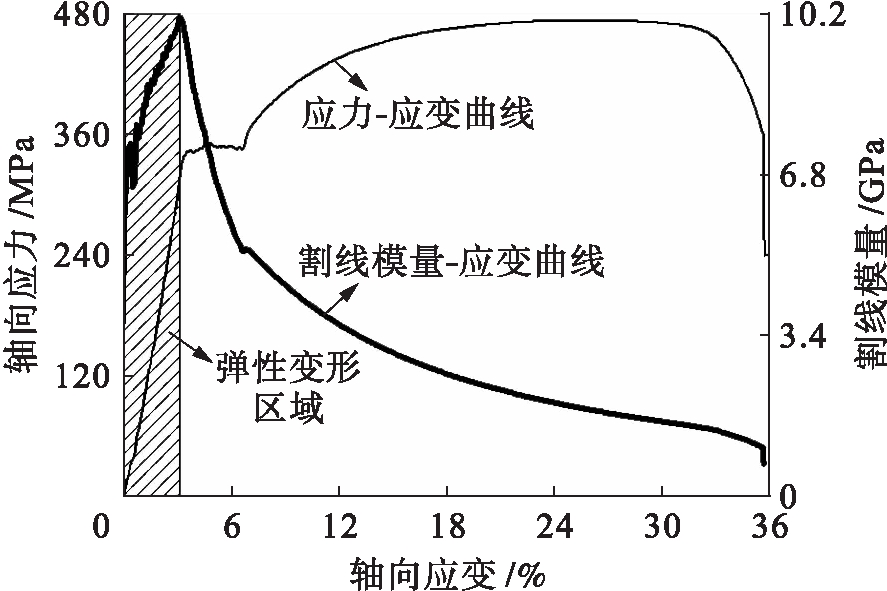
图2 低碳钢拉伸时的割线模量应变曲线
Fig.2 Secant modulus-strain curve of low carbon steel subjected to tension
由图2～5可见，在应变全过程中割线模量一直在变化，在轴向拉伸或压缩时两种材料的割线模量具有如下规律：
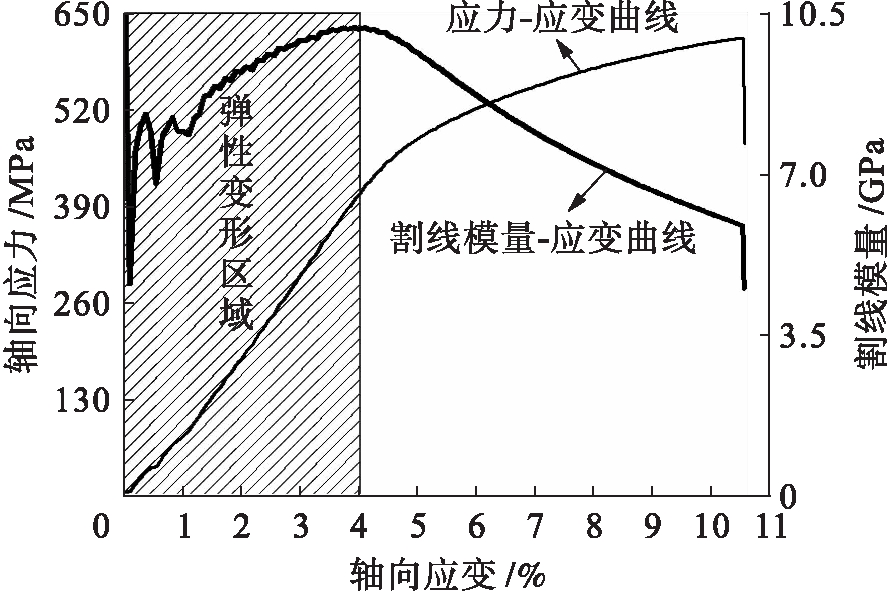
图3 高碳钢拉伸时的割线模量应变曲线
Fig.3 Secant modulus-strain curve of high carbon steel subjected to tension
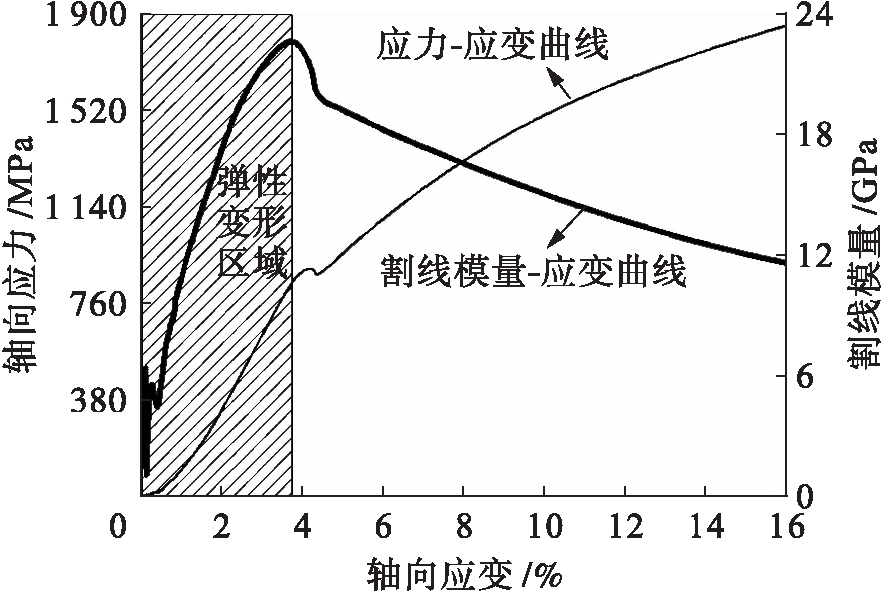
图4 低碳钢压缩时的割线模量应变曲线
Fig.4 Secant modulus-strain curve of low carbon steel subjected to compression
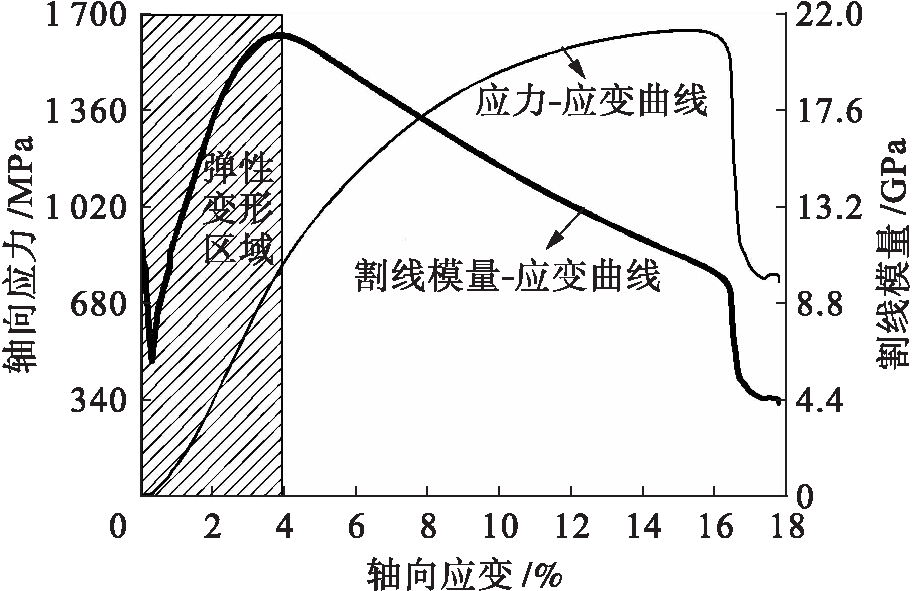
图5 高碳钢压缩时的割线模量应变曲线
Fig.5 Secant modulus-strain curve of high carbon steel subjected to compression
1) 在应变全过程中割线模量先增大后减小，且存在明显峰值，且达到峰值后出现衰减现象；
2) 低碳钢延性特征明显，其弹性极限较为明显，不管是拉伸还是压缩状态，割线模量峰值均出现在弹性与塑性变形转换点附近；
3) 高碳钢脆性特征明显，在应力应变曲线上弹性和塑性转换不明显，但割线模量峰值也出现在弹性和塑性变形转换点附近.
为了证明割线模量峰值在弹性极限附近这一观点，开展了高碳钢在不同应变阶段的卸载试验.若在割线模量峰值前卸载，其残余变形接近于零，而在割线模量峰值后卸载，残余变形显著增大，则证明割线模量峰值与弹性极限确实具有对应关系，至少弹性极限就在割线模量峰值附近.割线模量峰值为判定弹性极限的重要参考.鉴于篇幅原因，本文只给出高碳钢的卸载试验曲线.
由图5可知，高碳钢单轴压缩时割线模量峰值出现在3.8%应变处，故本文围绕3.8%应变处进行多次独立卸载试验，即每个试件只做一次卸载试验，不能重复使用.具体卸载点为0.5%、1.5%、2.5%、3%、3.5%、4%、4.5%与5%应变处共8种情况，卸载曲线如图6所示.由图6可以获取不同应变处卸载后的残余变形.由图6可见，随着卸载位置的改变，卸载后的残余变形随卸载点应变的增大而增大.
为了直观地表示残余变形的变化，以卸载点处的应变为横坐标，卸载后的残余变形为纵坐标，绘制高碳钢在不同应变处卸载后的残余变形曲线，结果如图7所示.由图7可知，当卸载点处的应变超过3.5%后，残余变形迅速增加，而图5中割线模量峰值出现在3.8%应变处，可见两者较为接近.像钢材这种典型的均质材料，其弹塑性变形转换是一个连续过程，不存在绝对的明确界限，而当应力超过弹性极限后，塑性变形则变为一个逐步累加的过程.
张克球等[4]在对不同等级的热轧钢筋进行力学试验后发现，其屈服前的塑性应变如表1所示.由图6f可见，在4%应变处卸载后，高碳钢的残余变形为0.058 5%，该残余变形与表1中热轧钢筋在屈服前的塑性变形较为接近，表明热轧钢筋的弹性极限确实在4%附近，也间接证明了本文提出的利用割线模量峰值判定弹性极限的方法具有可操作性.
通过以上试验研究，本文从不同角度证明了割线模量峰值与弹性极限或上屈服强度之间的相对固定关系，但割线模量峰值是否受试验条件的影响还需要进一步考证.需要进行进一步分析的主要问题为：
1) 割线模量峰值可能受加载速度或边界条件等试验条件的影响；
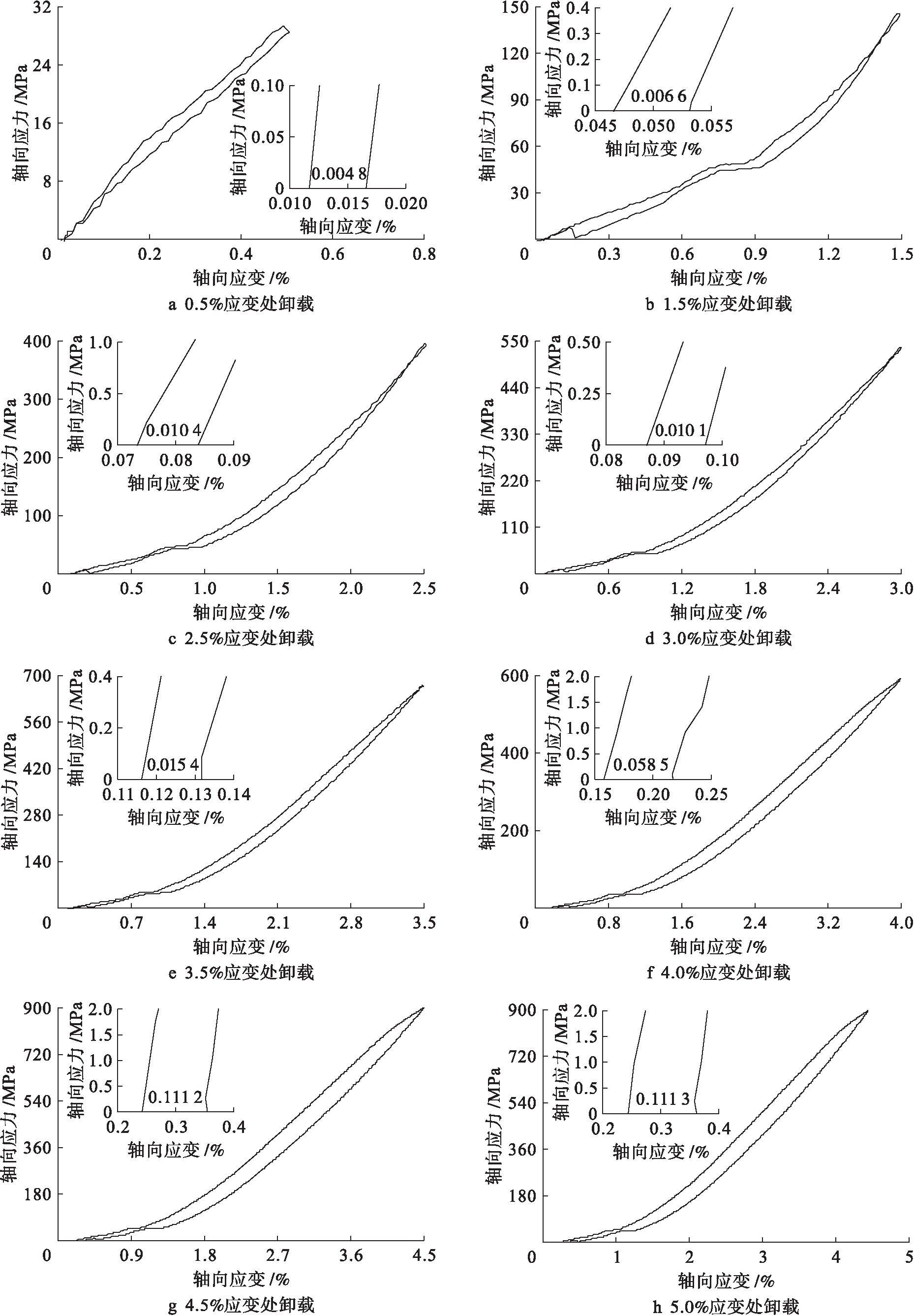
图6 高碳钢卸载后的应力应变曲线
Fig.6 Stress-strain curve of high carbon steel after unloading
2) 割线模量峰值可能与试件的尺寸或形状有关，即可能存在尺寸或形状效应；
3) 割线模量峰值可能与试件所处的应力状态有关.
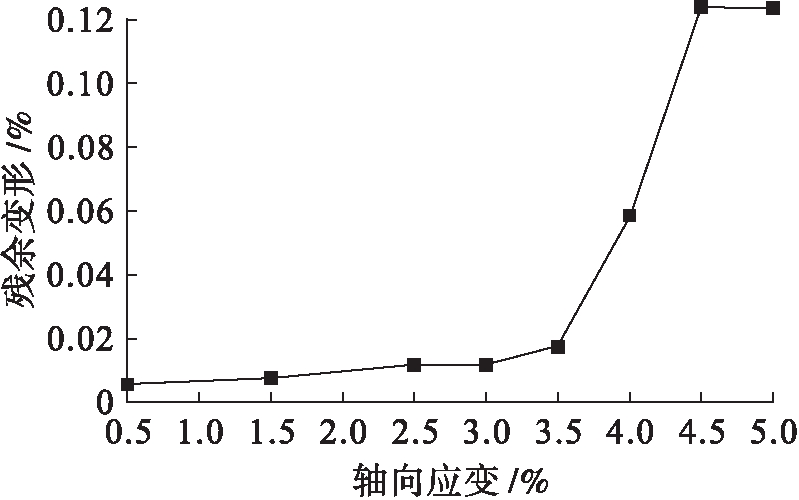
图7 高碳钢不同应变处卸载后的残余变形
Fig.7 Residual deformation of high carbon steel after unloading at different strain
表1 热轧钢筋屈服前塑性应变
Tab.1 Plastic strains of hot rolled bar before yield %
I级钢筋II级钢筋III级钢筋IV级钢筋≈00.040.050.042
总之，以上因素既影响了割线模量峰值，也会影响弹性极限本身，因此，上述因素是否会影响到割线模量峰值与弹性极限的对应关系，需要进行进一步的试验研究.
基于割线模量应变曲线，本文通过试验寻求割线模量峰值与弹性极限之间的关系，得出以下结论：
1) 低碳钢延性特征明显，当进行单轴拉伸或压缩时，其应力应变曲线的弹性极限较为明显，割线模量峰值与弹性极限的一致性较高；
2) 高碳钢表现出一定的脆性特征，单轴拉伸或压缩时应力应变曲线的弹性极限判定较为困难，而用割线模量峰值判定弹性极限较为方便，不同应变处的卸载试验也支持这一观点；
3) 割线模量可能与加载速度、边界条件、应力状态等因素有关，也可能存在尺寸或形状效应，这些因素是否影响两者的对应关系还需进一步研究.
[1] 陈四利，李艳宇，张精禹.基于三参数双τ2强度理论的厚壁圆筒极限压力分析 [J].沈阳工业大学学报，2016，38(5)：555-559.
(CHEN Si-li，LI Yan-yu，ZHANG Jing-yu.Limit stress analysis for thick-wall cylinder based on tri-parameter and twinτ2 strength theory [J].Journal of Shenyang University of Technology，2016，38(5)：555-559.)
[2] 姜志宏，王宝雨，校文超.低频振动作用下 45 钢压缩力学行为分析 [J].塑性工程学报，2017，24(2)：166-170.
(JIANG Zhi-hong，WANG Bao-yu，XIAO Wen-chao.Mechanical behaviors of steel 45 during compression in the low-frequency vibration [J].Journal of Plasticity Engineering，2017，24(2)：166-170.)
[3] 邱克强，胡冰，任鹤，等.低合金高强钢KMN 焊接接头的低温性能 [J].沈阳工业大学学报，2015，37(6)：634-638.
(QIU Ke-qiang，HU Bing，REN He，et al.Low-temperature properties of welded joints of KMN HSLA steel [J].Journal of Shenyang University of Technology，2015，37(6)：634-638.)
[4] 张克球，李承孝，范知言，等.钢筋应力应变特性初步分析 [J].工业建筑，1981，7(6)：16-19.
(ZHANG Ke-qiu，LI Cheng-xiao，FAN Zhi-yan，et al.Preliminary analysis on stress-strain characteristics of reinforcing steel bar [J].Industrial Construction，1981，7(6)：16-19.)
[5] 杨晶，白晓红.对采用割线模量法进行沉降计算所存在问题的探讨 [J].太原理工大学学报，2014，453(2)：274-278.
(YANG Jing，BAI Xiao-hong.Study on some problems of settlement calculation with secant modulus method [J].Journal of Taiyuan University of Technology，2014，453(2)：274-278.)
[6] 延西利，李新波，延凯凯，等.基于压缩试验的水泥混凝土弹性模量取值法 [J].长安大学学报(自然科学版)，2015，35(4)：1-7.
(YAN Xi-li，LI Xin-bo，YAN Kai-kai，et al.Determination of elastic modulus of cement concrete based on compression test [J].Journal of Chang’an University (Natural Science Edition)，2015，35(4)：1-7.)
[7] 谷川，王军，张婷婷，等.应力路径对饱和软黏土割线模量的影响 [J].岩土力学，2013，34(12)：3394-3402.
(GU Chuan，WANG Jun，ZHANG Ting-ting，et al.Influence of stress path on secant modulus of soft saturated clay [J].Rock and Soil Mechanics，2013，34(12)：3394-3402.)
[8] 张国凯，李海波，夏祥，等.岩石单轴压缩下能量与损伤演化规律研究 [J].岩土力学，2015，36(增刊1)：94-100.
(ZHANG Guo-kai，LI Hai-bo，XIA Xiang，et al.Research on energy and damage evolution of rock under uniaxial compression [J].Rock and Soil Mechanics，2015，36(Sup 1)：94-100.)
[9] Ahn J，Gabr M.Degraded secant modulus for permanent deformation of soils [J].International Journal of Pavement Engineering，2015，16(6)：549-558.
[10] Gomes R C，Jaime A S，Modaressi-Farahmand R，et al.Validation of a strategy to predict secant shear modulus and damping of soils with an elastoplastic model [J].Journal of Civil Engineering，2016，20(2)：609-622.
[11] 中国国家标准化管理委员会.GB/T 228.1-2010 金属材料拉伸试验第1 部分：室温试验方法 [S].北京：中国标准出版社，2011.
(China National Standardization Management Committee.GB/T 228.1-2010 Metallic materials tensile testing part 1：method of test at room temperature [S].Beijing：China Standards Press，2011.)