图1 现场检测仪表安装示意图
Fig.1 Schematic installation of on-site detection instruments
信息科学与工程
随着我国工业化水平的不断提高,人们对工件加工精度的要求也越来越高,因而要求生产出的工件与标准工件的误差应尽可能小,从而满足生产要求[1].水泵属于旋转机械,水泵转子是具有连续回转面的工件且为水泵的核心部件.对水泵转子进行径向圆跳动检测是工件加工中的一项重要指标[2-3].由于实际检测中的检测系统在装配过程中会出现轴的实际轴心与安装的旋转中心不重合的现象,因而使得检测得到的径向圆跳动值出现较大偏差.本文针对这一问题进行分析,分离出安装偏心,并得到较为准确的检测值,因而本文研究具有实际意义[4].
径向圆跳动是指当被测实际要素绕其回转中心旋转一周时,在无轴向移动的情况下直径方向上跳动量的最大值与最小值之差.径向圆跳动可以分为径向机械圆跳动和径向电气圆跳动两大类[5].在无轴向移动的情况下被检测工件绕基准轴旋转一周,在给定的直径测量方向上所测得的机械表面变化量的最大和最小示数之差称为径向机械圆跳动.在无轴向移动的情况下被检测工件绕基准轴旋转一周,在给定的直径测量方向上所测得的电磁和应力等特性变化量的最大和最小示数之差称为径向电气圆跳动[6].
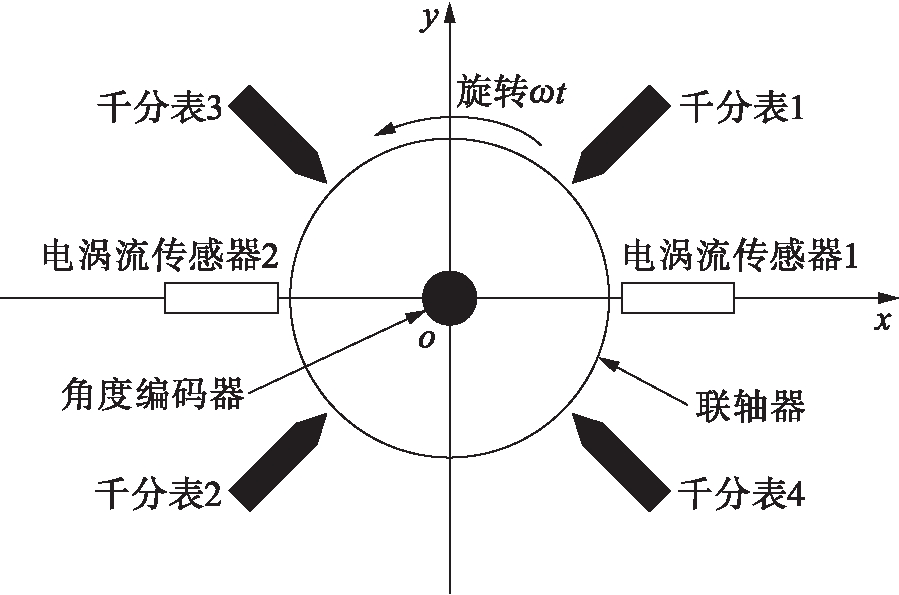
经过多次检测后发现,现场检测的径向机械圆跳动数据中安装偏心引起的误差较大.在检测过程中水泵轴安放于V型槽上且通过电机驱动而转动.因此,电机的驱动轴与被测水泵轴的安装可能存在偏心误差.通过对电机联轴器进行跳动检测与数据处理,可以验证本文方法消除偏心误差的可行性.现场检测仪表安装示意图如图1所示.

图1 现场检测仪表安装示意图
Fig.1 Schematic installation of on-site detection instruments
当进行检测时,在0°与180°两个方向上各安装一组电涡流传感器进行综合跳动检测,且分别记为电涡流传感器1与电涡流传感器2.利用综合跳动数据配合径向机械圆跳动检测数据,即可分离出径向电气圆跳动数据.在45°与225°两个方向上安装第一组千分表进行径向机械圆跳动检测,分别记为千分表1和千分表2.在135°和-45°两个方向上安装第二组千分表同样进行径向机械圆跳动检测,分别记为千分表3和千分表4.角度编码器安装在联轴器中心同步进行角度检测.
因为在实际的径向圆跳动检测中存在误差和干扰,所以不能简单地将检测得到的电涡流传感器和千分表的变化量直接用于跳动计算.在本文系统中偏心误差的影响最为严重,因此,需要通过数据分析和处理将偏心误差去除,从而得到正确的跳动结果.
偏心误差实际上是由于旋转物体的几何中心与实际旋转中心不重合所引起的误差[7].如果检测旋转体的径向横截面为标准圆,在无偏心的情况下传感器的检测值始终为一个固定值,即显示曲线呈现为一条直线.在存在偏心的情况下显示曲线呈现正弦规律[8].不过偏心是可以被纠正和补偿的.
偏心误差原理与显示曲线如图2所示.其中:轴半径为r,真实的半径偏差值为Δr(随角度不同而变化);轴的圆心为o′,驱动旋转中心为o;偏心量为e,传感器偏移量为ε;检测点至横轴的垂线距离为p.
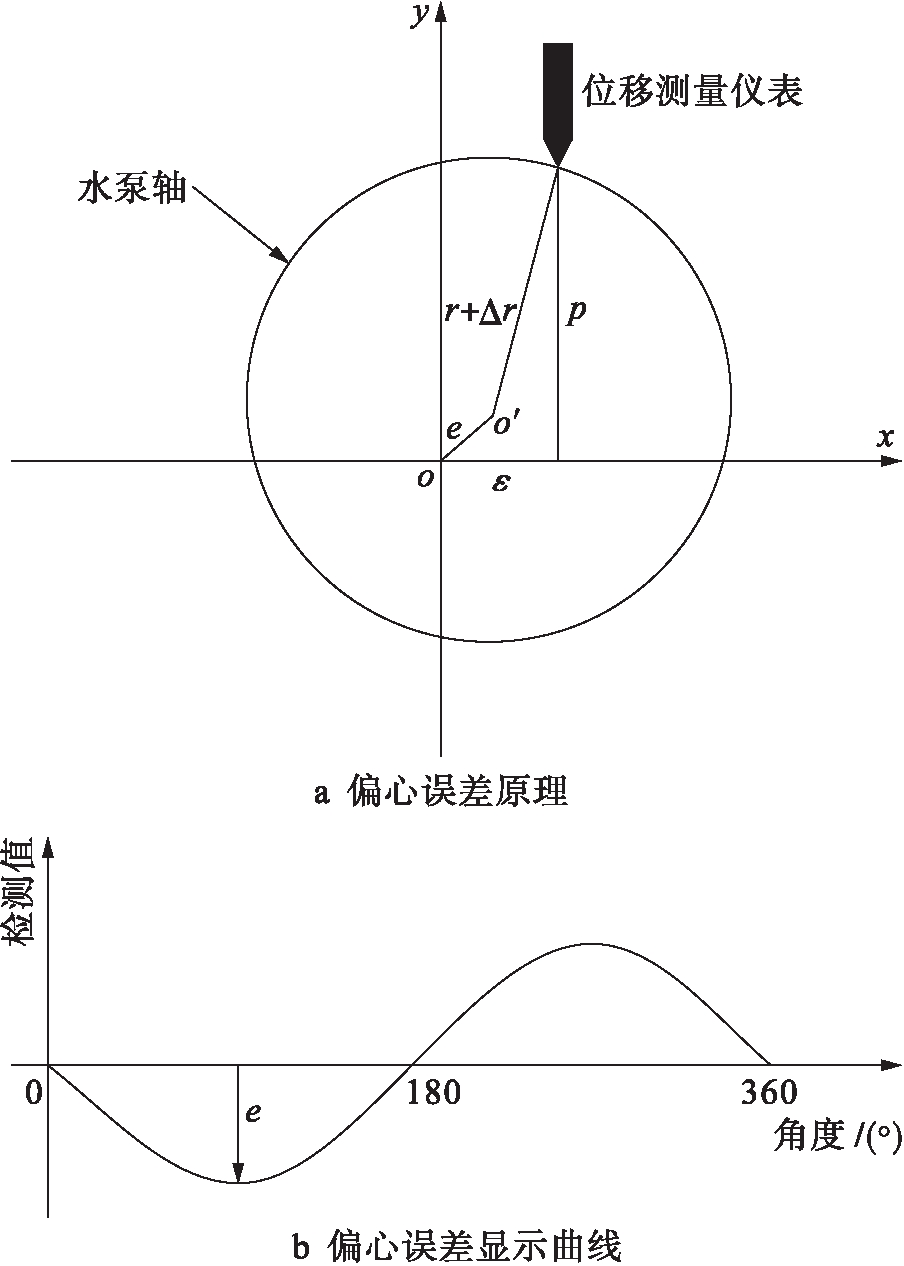
图2 偏心误差原理与显示曲线
Fig.2 Principle and display curve of eccentric error
由存在安装偏心的轴横截面示意图可以得出各个变量之间的关系,即
(1)
式中:ω为旋转角频率;θ为初相位.
由于r+Δr≫ε-ecos(ωt+θ),故
p≈esin(ωt+θ)+r+Δr
(2)
由于位移测量仪表测量的是径向变化量,而仪表可能带有初值且初始位置点随机,因而通常将传感器检测的数据去除平均值,从而使其呈现出相对于中间值的正负变化形式.
检测值的计算公式为
d=p-mean(p)
(3)
式中,mean(p)为p的所有测量值的平均值.
由检测值绘制的曲线随着物体的旋转将呈现幅值为e的正弦规律,即偏心误差将引起显示曲线的正弦变化规律[9].通常真实的半径偏差值Δr是随机的,由于检测值中去掉了常数项,故将不包含轴半径r,即
d≈esin(ωt+θ)+Δr-mean(Δr)
(4)
径向圆跳动值的计算表达式为
RO=max(d)-min(d)
(5)
如果直接利用检测值计算径向圆跳动,则会将安装偏心代入跳动值中,从而导致计算错误.
当进行实际测量时,安装了2个电涡流传感器和4个千分表,并在水泵轴联轴器旋转一周的不同角度下进行测量.以角度作为横坐标,检测值作为纵坐标,将电涡流传感器和千分表检测的数据绘制成曲线,结果如图3所示.由图3a~c可见,电涡流传感器和千分表的检测结果均呈现正弦曲线规律.图3d~f是在检测值的基础上增加一定半径绘制得到的极坐标曲线.由图3d~f可以直观地观察到偏心现象,表明水泵轴的安装轴线与实际水泵轴的几何轴线不重合,因而存在偏心误差,且偏心误差的影响较大.因此,需要将偏心误差分离出来.
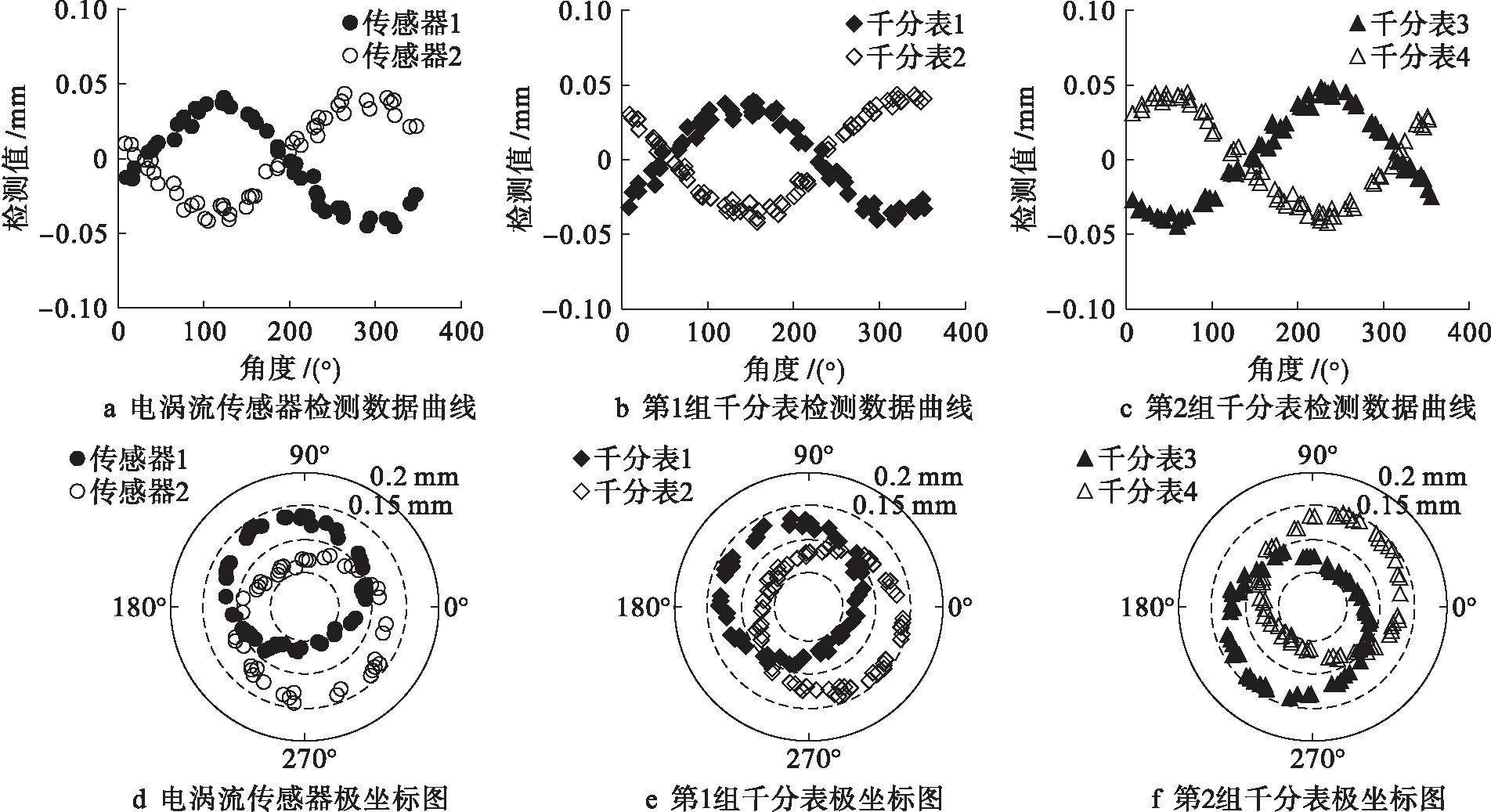
图3 检测数据曲线与极坐标图
Fig.3 Curves of detection data and polar diagrams
通过实验可以获得一组关于角度与检测值的离散点集,即
I={(αi,di),i=1,2,…,m}
(6)
式中:αi为各个检测点的角度值;di为各个检测点的检测值(已去除平均值);m为检测点的个数.
通过绘制曲线可以得到角度与拟合检测值的基本变化规律为
(7)
式中:![]() 为拟合检测值;A为拟合曲线幅度值.
为拟合检测值;A为拟合曲线幅度值.
由于αi=ωti+θ,且ti为第i个取样时刻,因此,拟合函数式可以表示为
(8)
式中,n为拟合参数的组数,数值上与位移测量仪表的数目相等.通过最小二乘法拟合求得一组最佳参数An与θn,使得拟合曲线的拟合离差平方和最小.
拟合离差可以表示为
(9)
拟合曲线的拟合离差平方和可以表示为
(10)
运用最小二乘法拟合原始数据曲线[10]后对照式(4)与(8),即可得到偏心误差的对应关系.拟合得到的参数An实际上就是安装产生的偏心量,而参数θn即为测量时的初相位.利用相应拟合函数即可求出各测量时刻由偏心产生的误差.
此外,将各个角度处的检测值减去各个角度拟合出的偏心误差,即可得到去除平均值后半径的偏差值,即
(11)
利用式(11)可以得到更准确的径向圆跳动值,其表示式为
RO′= max(Δri)-min(Δri)≈
max(δi)-min(δi)
(12)
为了表明电涡流和千分表的具体拟合情况,绘制出相应的拟合曲线,结果如图4所示.由图4可见,检测数据符合拟合函数的变化规律.
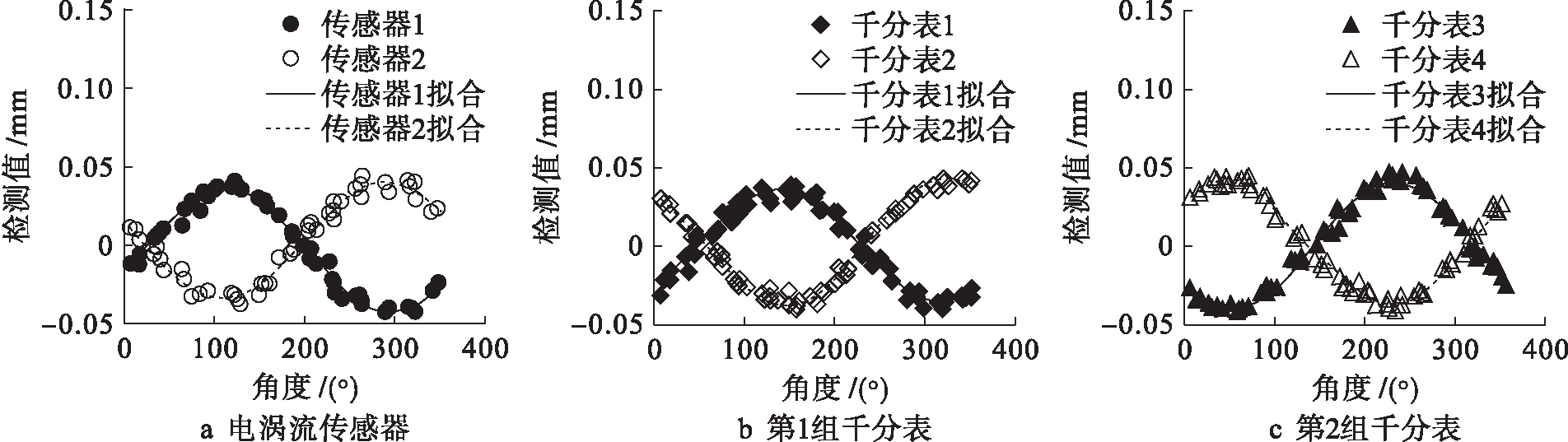
图4 拟合曲线
Fig.4 Fitting curves
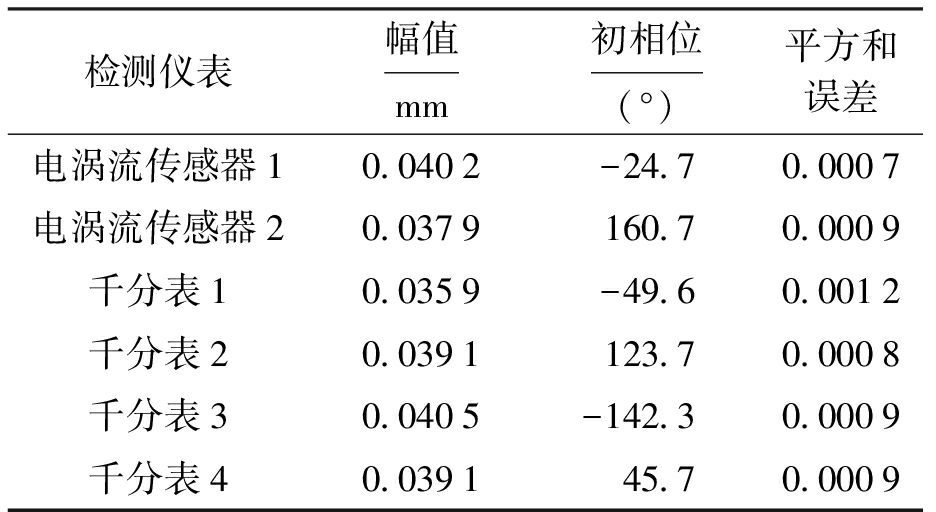
表1为通过拟合求得的拟合参数,包括拟合曲线幅值、初相位及平方和误差.由表1可见,拟合后的偏心距约为40 μm,表明同一被测工件测量结果的一致性较好.电涡流传感器1、2,千分表1、2以及千分表3、4安装时的相位分别两两相差约180°.观察表1可知,拟合后上述仪表的两两相位差也约为180°,因而符合原始数据规律.同时,检测点的拟合平方和误差约为0.000 9.可见,拟合曲线符合原始数据的变化规律.
表1 拟合参数
Tab.1 Fitting parameters
检测仪表幅值mm初相位(°)平方和误差电涡流传感器10.0402-24.70.0007电涡流传感器20.0379160.70.0009千分表10.0359-49.60.0012千分表20.0391123.70.0008千分表30.0405-142.30.0009千分表40.039145.70.0009
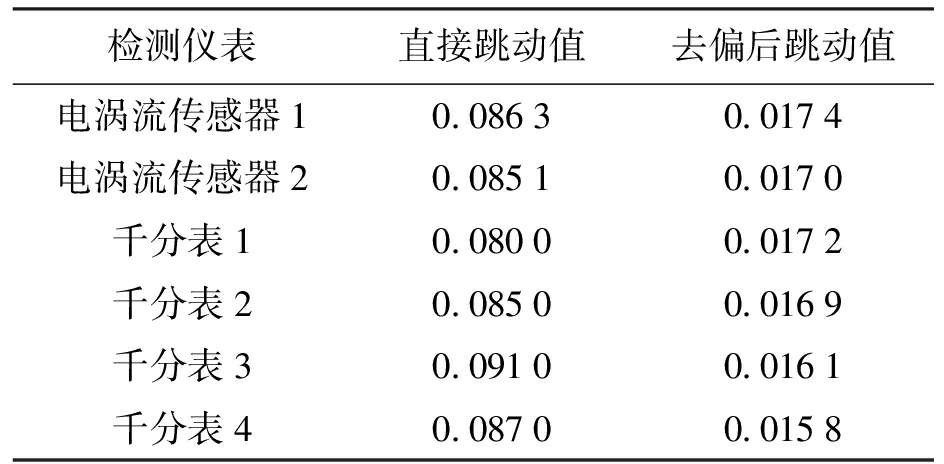
数据处理前后跳动值的比较结果如表2所示.由表2可见,数据处理前跳动值处于80~91 μm之间,数据处理后的跳动值集中在15.8~17.4 μm之间,且处于位移测量仪表的测量精度范围内.
表2 误差处理前后跳动值比较
Tab.2 Comparison in runout values before and after error treatment mm
检测仪表直接跳动值去偏后跳动值电涡流传感器10.08630.0174电涡流传感器20.08510.0170千分表10.08000.0172千分表20.08500.0169千分表30.09100.0161千分表40.08700.0158
图5为原始检测数据去偏后的数值与极坐标图.由图5a~c可见,经过处理后的数据均集中于-10~10 μm区间内,数据跳动量大幅下降,因而提高了检测精度.由图5d~f可见,由处理后的数据绘制得到的圆已经是以坐标原点为圆心的圆,不再存在偏心现象,表明本文方法可以很好地分离出由偏心引起的误差.
通过进行实地检测获得了检测数据值,对检测数据进行了理论分析,明确了偏心误差的影响.通过进行最小二乘曲线拟合,获得偏心距和初相位.结果表明,偏心距约为40 μm,拟合平方和误差约为0.000 9.本文实现了偏心误差的误差分离,可将偏心误差从检测值中分离出去,从而获得较为准确的跳动值.电涡流传感器、千分表检测得到的跳动值由原来的80~91 μm下降至15.8~17.4 μm,且修正后各组跳动值之间的一致性较好.
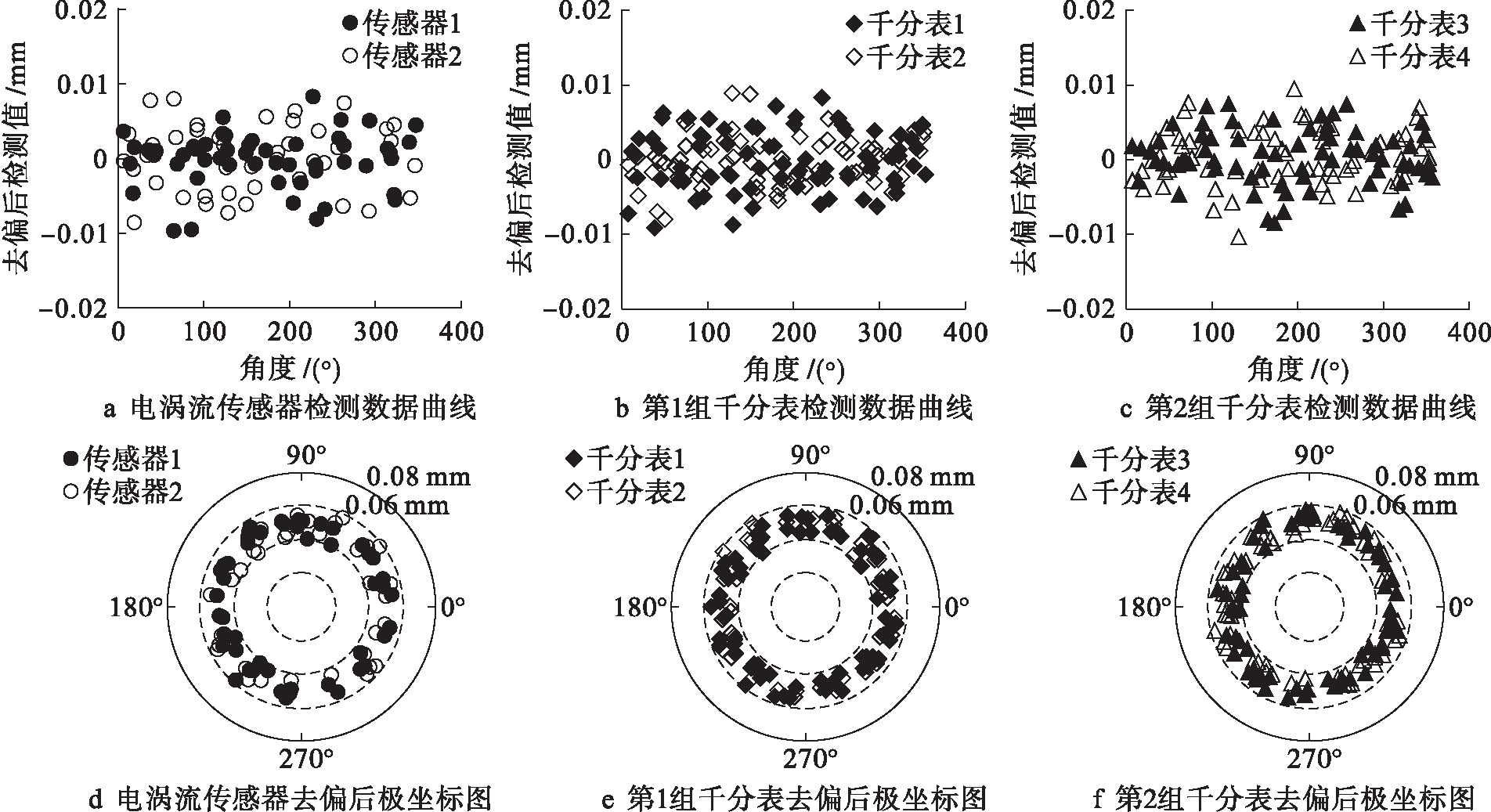
图5 去偏后检测数据曲线与极坐标图
Fig.5 Curves of detection data and polar diagrams after removing eccentricity
[1] 熊四昌,庄首.基于DSP的车辆轮毂跳动量检测系统 [J].电机工程,2015,32(4):488-492.
(XIONG Si-chang,ZHUANG Shou.Detect system of vehicle wheel detection machine based on DSP [J].Journal of Mechanical & Electrical Engineering,2015,32(4):488-492.)
[2] 赖海鸣,林载誉,杨将新,等.大型轴类电跳动在位测量系统 [J].汽轮机技术,2014,56(3):234-236.
(LAI Hai-ming,LIN Zai-yu,YANG Jiang-xin,et al.Large shaft electrical runout on-machine measuring system [J].Turbine Technology,2014,56(3):234-236.)
[3] 陈虹,朱颖.高速旋转主轴径向跳动非接触测量 [J].机电工程技术,2013,42(1):72-75.
(CHEN Hong,ZHU Ying.High-speed rotating spindle non-contact measurement radial direction runout value of research [J].Mechanical and Electrical Engineering,2013,42(1):72-75.)
[4] 杨刚.高速电主轴径向跳动及静刚度测试方法 [J].重庆理工大学学报,2013,27(2):62-68.
(YANG Gang.Research of high-speed electronic spindle radius run-out and static stiffness [J].Journal of Chongqing University of Technology,2013,27(2):62-68.)
[5] 茅健,陈小龙,林载誉,等.轴类零件电跳动在位测量方法 [J].农业机械学报,2014,45(5):310-314.
(MAO Jian,CHEN Xiao-long,LIN Zai-yu,et al.On-site measuring method for electrical runout on main shaft [J].Transactions of the Chinese Society for Agricultural Machinery,2014,45(5):310-314.)
[6] 宋起,单东日.大型轴类工件径向圆跳动非接触检测方法的研究 [J].组合机床与自动化加工技术,2015(8):74-78.
(SONG Qi,SHAN Dong-ri.Research on non-contact measurement method of the radial circular run-out error of the large-size axes [J].Modular Machine Tool & Automatic Manufacturing Technique,2015(8):74-78.)
[7] Li J S,Yu Y J,Xue Y J.Forecast for radial runout of outer ring in cylindrical roller bearing [J].Procedia CIRP,2017,62:375-379.
[8] 高加琼,魏霖静.基于最小二乘及分类向量机的空气调节器故障检测 [J].沈阳工业大学学报,2016,38(3):326-330.
(GAO Jia-qiong,WEI Lin-jing.Fault detection of air conditioner based on least squares and support vector machine classification [J].Journal of Shenyang University of Technology,2016,38(3):326-330.)
[9] 刘忠夫,王振宏.回转主轴垂直度及安装偏心对轮毂跳动检测的影响分析 [J].长春理工大学学报(自然科学版),2016,39(2):35-38.
(LIU Zhong-fu,WANG Zhen-hong.Analysis on effect of rotary axis perpendicular and installation eccentric to the wheel hub runout detection [J].Journal of Changchun University of Science and Technology (Natural Science Edition),2016,39(2):35-38.)
[10] 颜华,李欣,王善辉.基于最小二乘法和克里金插值的三维温度场重建 [J].沈阳工业大学学报,2014,36(3):303-307.
(YAN Hua,LI Xin,WANG Shan-hui.Reconstruction of three-dimensional temperature field based on least square method and Kriging interpolation [J].Journal of Shenyang University of Technology,2014,36(3):303-307.)