控制工程
机场的停机位是飞机在地面上的停放位置.机场停机位的分配需要考虑班机机型大小、起降时刻和停机位容量等多种因素,需要在一定时限内,由机场调度指挥中心为进港和出港班机指定合适的停机位,以保证班机的正常起降而不发生延误.然而,班机会因为恶劣的天气、机身机械问题、机场安全问题、机场拥挤、机场之间的延迟传播等多种因素导致延误,使班机离到港时刻表发生较大变化.同一停机位如果某个班机的离港时刻晚于其他班机的到港时刻,班机的调度就会出现冲突.机场停机位管理人员的日常任务之一就是如何合理地再分配有冲突的班机.如果这种再分配没有适当的决策支持工具,会给停机位管理人员带来巨大的困难.科学、高效的停机位再分配是机场各项工作顺利进行的有效保障,是提升民航产业服务能力和竞争力的重要环节.
对于停机位再分配算法,国内外很多研究人员从不同角度进行了广泛而深入的实验研究.Dorndorf等使用图论中的团划分模型解决了确定性和随机性的停机位再分配问题[1];涂浩以延误的过站航班为研究对象,提出了一种对延误的过站航班预分配停机位的再分配方案[2];陈前等基于遗传算法,建立了以避免冲突为约束的安全停机位再分配模型[3];刘长有等人采用粒子群遗传算法,考虑避免潜在的航班双推冲突问题,提出了基于运行安全的停机位再分配优化模型[4];Yu等考虑了滑行道调度问题,提出一种新的启发式算法,对每种调度进行成本评估和冲突检测,求解停机位再分配问题[5];Wang等建立了基于停车位重新分配导致的干扰与惩罚最小的目标函数,采用蚁群算法验证了模型的有效性[6];李亚玲等针对机场最大化停机位利用率以及最小化旅客行走路程问题,提出了一种动态、灵活分配停机位的禁忌搜索算法[7];Deng等将遗传算法和蚁群优化算法相结合,提出了一种两阶段混合算法(GAOTWSH),用于求解延迟停机位重新分配问题[8].
从目前对停机位再分配的研究中可以看出,大多只单方面考虑机场的利益,兼顾乘客满意度的模型较少.即便选用多目标优化模型,综合考虑了机场和乘客双方利益,但模型计算时间较长.本文是在多商品网络流停机位分配模型[9]的基础上,对停机位再分配模型作进一步研究,建立了以飞机燃油消耗成本和对乘客舒适度影响最小为目标的实时再分配模型.该模型兼顾了机场和乘客的利益,有效减少了对既存的航班分配方案影响程度,降低了传统机场再分配模型的时间消耗,具有较好的实时性.
停机位再分配问题是指在已分配好初始停机位的基础上,根据航班时刻的实时变化,对停机位初始分配方案进行实时调整,使得航班的停机位分配更加合理.一般是在确定了延误航班的到/离港信息的情况下,对延误航班和相关航班的停机位分配做出调整,以满足旅客和机场各部门的要求.研究对象是一个时间段内一组航班和一组停机位之间的调整.研究目的是在原分配方案的基础上得到一个新的分配方案,提高机场的运营效率,降低运营费用,提升旅客的满意度.
本文提出的停机位实时再分配模型解决了以下几个问题:
1) 使机场的运营成本最低,降低了飞机的燃油消耗;
2) 尽最大可能提高旅客的舒适度,减少由于再分配导致的麻烦;
3) 短时间内完成停机位的再分配,一般在1 min内完成;
4) 再分配后的结果对其他班机的影响较小.
为了解决上述问题,本文提出了多商品网络流停机位实时再分配模型.将停机位映射为商品,这些商品在源节点和终节点之间通过到达节点和离开节点连接.当连接节点之间的弧可用时商品会流经弧,即停机位可分配给该航班,否则不可分配给该航班.
基于多商品网络流模型,本文对停机位实时再分配模型做出如下假设:
1) 所有的停机位可提供再分配,能够容纳任何尺寸的飞机;
2) 仅有一条跑道提供起飞和降落;
3) 假设所有尺寸飞机飞行时燃料费相同;
4) 假设所有尺寸飞机怠速时燃料费相同.
本文使用的数学符号定义如下:
1) 集合符号.F为所有未降落班机集合;N为停机位有冲突班机集合;K为全部停机位集合.
2) 参数符号.fi为班机i空中平均飞行时间;dik为班机i到停机位k(k∈K)的距离;ci为班机i飞行时单位距离燃料费;![]() 为班机i怠速时单位距离燃料费;ai为班机i到达和乘客开始登机缓冲时间;bk为停机位k在班机到达和乘客开始登机的缓冲时间;M为一个足够大的常数;t为当前时刻;l为再分配的次数;n为集合N的大小;vp为预先设定的惩罚阈值;vg为预先设定的间隙阈值;p′为一个班机离港再分配的惩罚值.
为班机i怠速时单位距离燃料费;ai为班机i到达和乘客开始登机缓冲时间;bk为停机位k在班机到达和乘客开始登机的缓冲时间;M为一个足够大的常数;t为当前时刻;l为再分配的次数;n为集合N的大小;vp为预先设定的惩罚阈值;vg为预先设定的间隙阈值;p′为一个班机离港再分配的惩罚值.
3) 决策变量符号.Xik为二值变量,当且仅当班机i被分到停机位k时为1;Zijk为二值变量,当且仅当班机i和j依次都被分配到停机位k时为1.
4) 辅助变量符号.Yik为二值变量,当且仅当班机i在前次更新被分配给停机位k时为1,即等于时间t-Δt时的Xik;Ai为随机变量,班机i到达时刻.
为了使停机位再分配既能同时兼顾机场和乘客的利益,又能提供短时间突发事件的处理能力,根据多商品网络流模型提出了如下目标函数,即
(1)
式中:I(-∞,vp](x)为分段函数,且![]() 为航班预期离港或到港时刻;Conflictijk为航班到港时刻或离港时刻有冲突的航班集合.目标函数分三部分,第一项表示停机位再分配发生在班机i离开始发机场后,距离目的地机场的剩余时间间隔在(-∞,vp]范围内的燃料费用变化.给定一个惩罚因子p′,用于减少旅客已经收到转机登机信息后再调整的错误发生.目标函数第二项表示班机i被再分配到停机位k导致燃料费用的变化.目标函数第三项表示班机j等待班机i离开停机位k导致燃料费用的变化.式(1)中,
为航班预期离港或到港时刻;Conflictijk为航班到港时刻或离港时刻有冲突的航班集合.目标函数分三部分,第一项表示停机位再分配发生在班机i离开始发机场后,距离目的地机场的剩余时间间隔在(-∞,vp]范围内的燃料费用变化.给定一个惩罚因子p′,用于减少旅客已经收到转机登机信息后再调整的错误发生.目标函数第二项表示班机i被再分配到停机位k导致燃料费用的变化.目标函数第三项表示班机j等待班机i离开停机位k导致燃料费用的变化.式(1)中,
I(-∞,vp](E(Ai)-fi-t)=
(2)
(3)
式(2)表示班机i离港后剩余时间间隔,当且仅当剩余时间间隔小于等于给定的阈值vp时为1,否则为0,即i不需要重新分配停机位.式(3)表示当班机i被再分配到另一个停机位k时求和结果为1.
模型需要满足以下约束条件:
(4)
(5)
(6)
E(Aj)+(1-Zijk)M≥E(Ai)+ai+bk (i,j∈F,k∈K)
(7)
Xik+Xjk=1 (i,j∈N,k∈K)
(8)
(9)
Xik,Zijk∈{0,1}
(10)
约束(4)表示一个班机只能分配到一个停机位;约束(5)、(6)表示引进中间决策变量;约束(7)表示班机i、j之间的先后顺序;约束(8)表示强制重分配集合N中的班机;约束(9)表示再分配级别的限制;约束(10)表示二值决策变量.
符号Ai是一个随机变量,对于每天给定的航线,其分布随时间发生变化.对于某个特定的班机,它的预期到港时刻E(Ai)可以通过预测天气状况来进行合理预测.一些与天气相关的预测包括如下变量:风速、风向、能见度、温度、云层和大气压等.多元回归模型可以拟合历史数据来为特定航线预测班机的延误,一旦得到了回归模型,就可以通过使用由机场提供的天气预报来估计班机的延迟,拟合的质量可以由R平方统计量进行测量.
由目标函数的特点可知,本文模型属于二值混合整数规划模型,求解步骤如下:
1) 按E(Conflictijk)>vg构造班机冲突集合N,如果N不为空转到步骤2);
2) 运行一个优化程序来分配相关班机;
3) 反复重新分配不同级别直至达到满意的最小值,此算法在一个固定的时间间隔t为15 min重复执行一次或者根据实际情况调整.
班机i被再分配到停机位k后可能会导致许多班机和停机位重新分配,因此发生再分配的班机需要控制分配次数.当用户指定参数l后,算法中再分配班机最大数量为N·l.在实践中,可选取l的几个不同值代入目标函数中计算求解,在得到的几个新分配方案中选择一个最佳方案.
采用国内某大型机场的某一天具体班机时刻表为例,选定一个时间段内空闲的10个停机位(G1,G2,…,G10),对20个即将到达的班机按照上述模型算法进行分配,使用由IBM公司开发的ILOG优化软件进行求解.班机i到港时刻E(Ai)和从另一个机场离港时刻E(Di)如表1所示.
表1 班机时刻表(实例1)
Tab.1 Flight schedule (example 1)
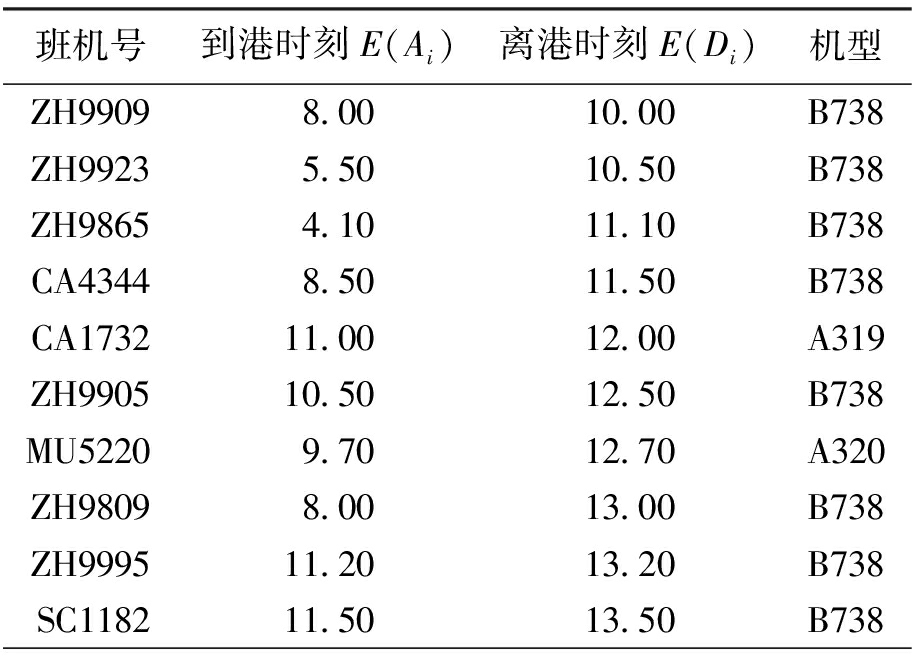
班机号到港时刻E(Ai)离港时刻E(Di)机型ZH99098.0010.00B738ZH99235.5010.50B738ZH98654.1011.10B738CA43448.5011.50B738CA173211.0012.00A319ZH990510.5012.50B738MU52209.7012.70A320ZH98098.0013.00B738ZH999511.2013.20B738SC118211.5013.50B738
表1(续)
Tab.1(Cont)
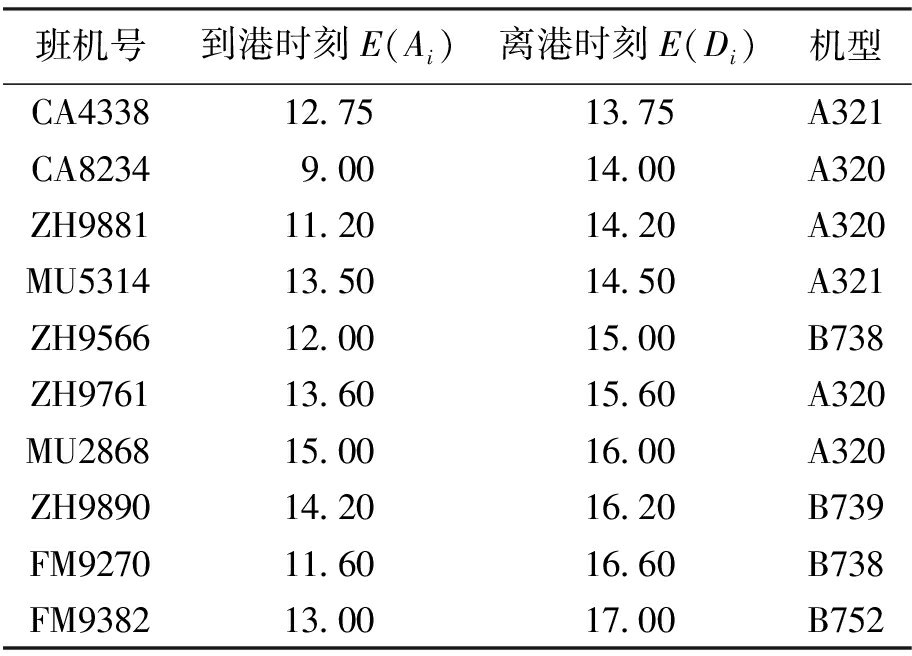
班机号到港时刻E(Ai)离港时刻E(Di)机型CA433812.7513.75A321CA82349.0014.00A320ZH988111.2014.20A320MU531413.5014.50A321ZH956612.0015.00B738ZH976113.6015.60A320MU286815.0016.00A320ZH989014.2016.20B739FM927011.6016.60B738FM938213.0017.00B752
模型中各参数取值为:班机i到达和乘客开始登机的缓冲时间ai与停机位k在班机到达和乘客开始登机的缓冲时间bk均为0.5 h,设惩罚阈值vp为2 h,间隙阈值vg为0.25 h,班机离港再分配的惩罚值p′为350元,班机i飞行时单位距离燃料费ci为28元,班机i怠速时单位距离燃料费![]() 为35元,当前时刻t为9时(GMT),再分配的次数为1,较大数M=8 888.
为35元,当前时刻t为9时(GMT),再分配的次数为1,较大数M=8 888.
表2中初始停机位的分配方案采用参考文献[9-10]算法计算得到.
表2 初始停机位分配方案
Tab.2 Initial gate reassignment scheme
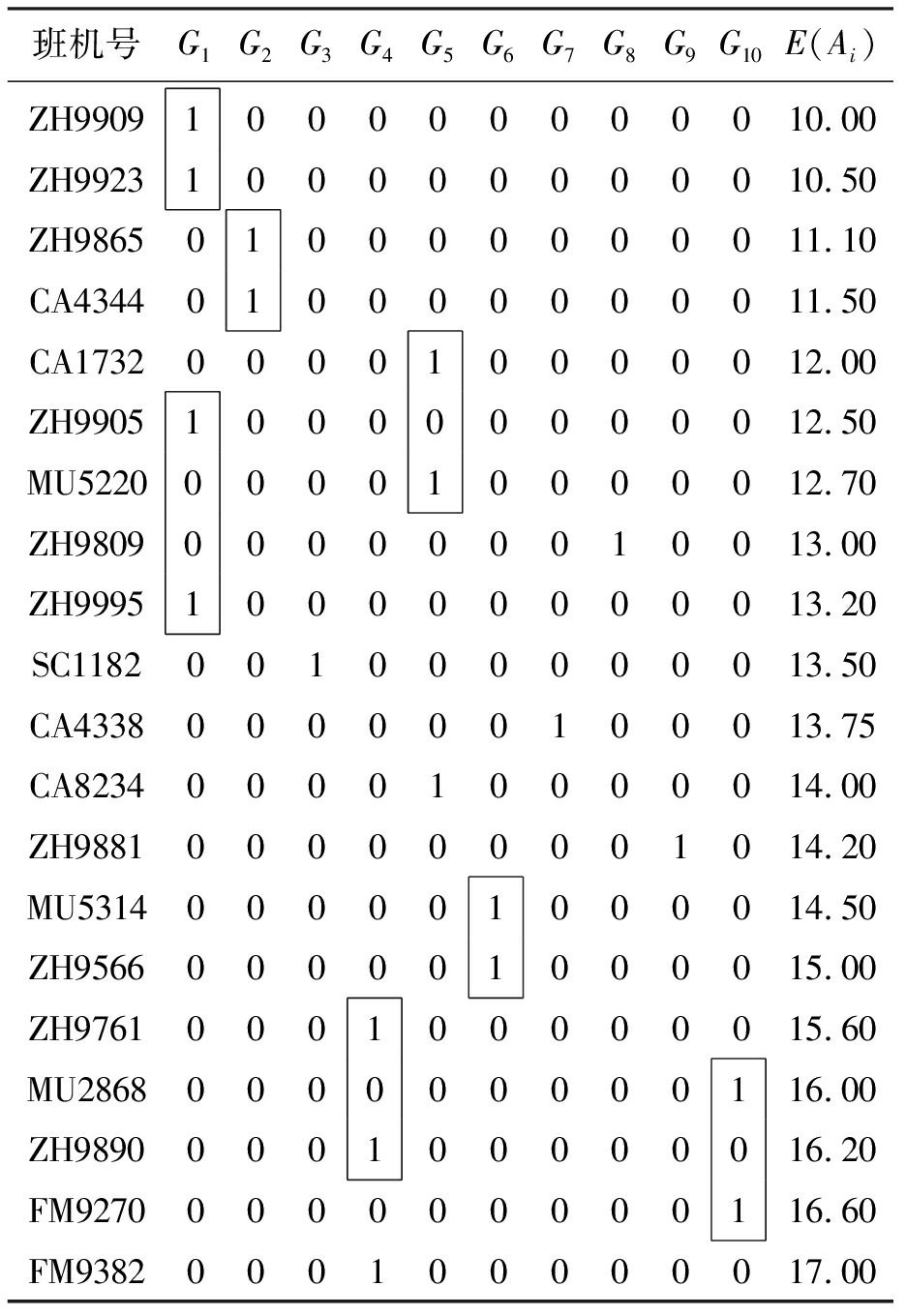
班机号G1G2G3G4G5G6G7G8G9G10E(Ai)ZH9909100000000010.00ZH9923100000000010.50ZH9865010000000011.10CA4344010000000011.50CA1732000010000012.00ZH9905100000000012.50MU5220000010000012.70ZH9809000000010013.00ZH9995100000000013.20SC1182001000000013.50CA4338000000100013.75CA8234000010000014.00ZH9881000000001014.20MU5314000001000014.50ZH9566000001000015.00ZH9761000100000015.60MU2868000000000116.00ZH9890000100000016.20FM9270000000000116.60FM9382000100000017.00
表2中,方框中数字1标注的班机表示有冲突.使用ILOG软件编写程序得到停机位再分配结果如表3所示,计算时间为0.093 75 s.
表3 停机位再分配方案(实例1)
Tab.3 Gate reassignment scheme (example 1)
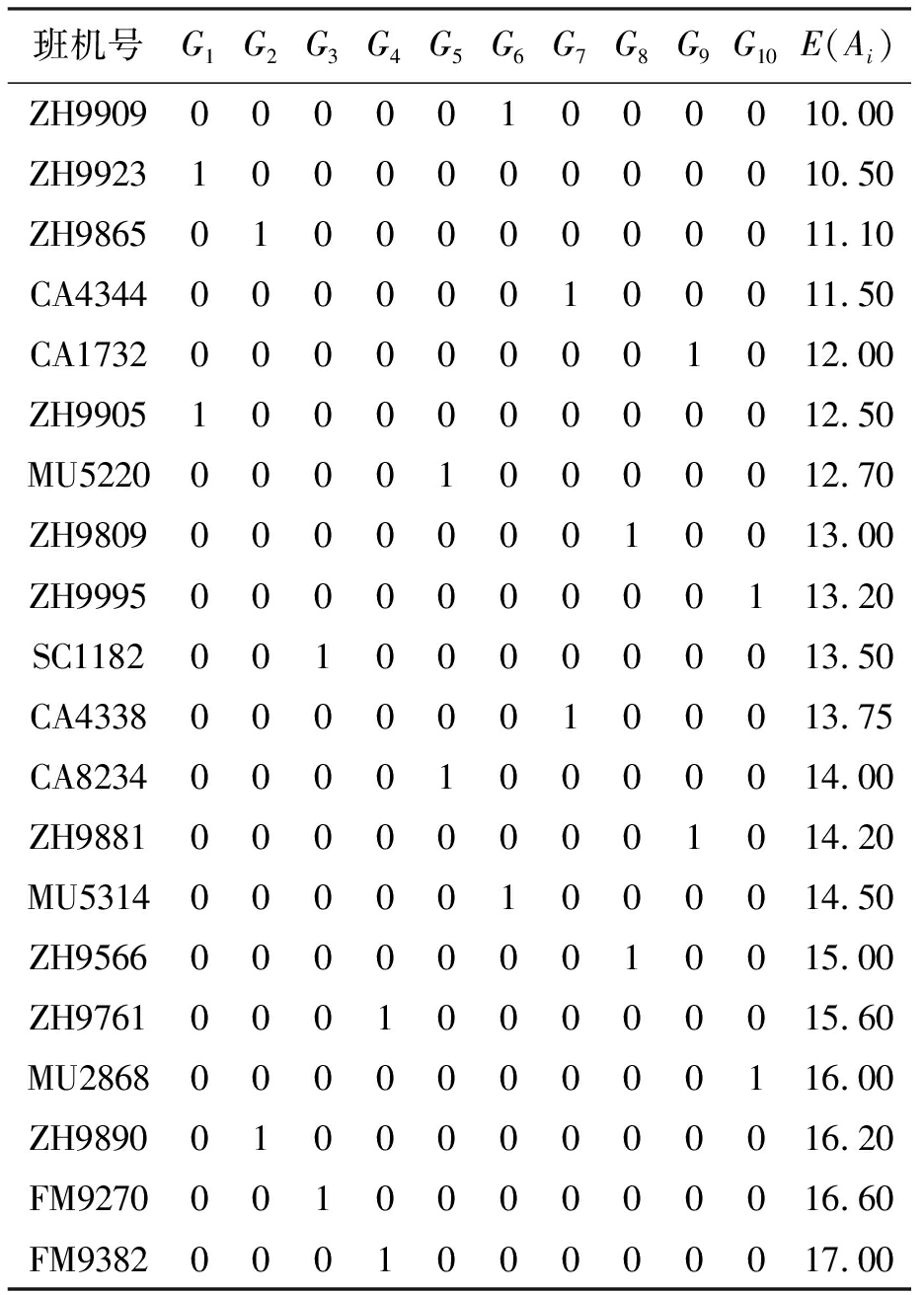
班机号G1G2G3G4G5G6G7G8G9G10E(Ai)ZH9909000001000010.00ZH9923100000000010.50ZH9865010000000011.10CA4344000000100011.50CA1732000000001012.00ZH9905100000000012.50MU5220000010000012.70ZH9809000000010013.00ZH9995000000000113.20SC1182001000000013.50CA4338000000100013.75CA8234000010000014.00ZH9881000000001014.20MU5314000001000014.50ZH9566000000010015.00ZH9761000100000015.60MU2868000000000116.00ZH9890010000000016.20FM9270001000000016.60FM9382000100000017.00
由表3可知,每个停机位调整的班机最多是2个,保证了对班机的调整尽可能少,降低了班机调整给乘客带来的不必要麻烦,提高了乘客的满意度.
在实验一的基础上,加大航班规模,选取某航空公司40个航班的到港和离港时刻作为基础数据,如表4所示.
表4 班机时刻表(实例2)
Tab.4 Flight schedule (example 2)
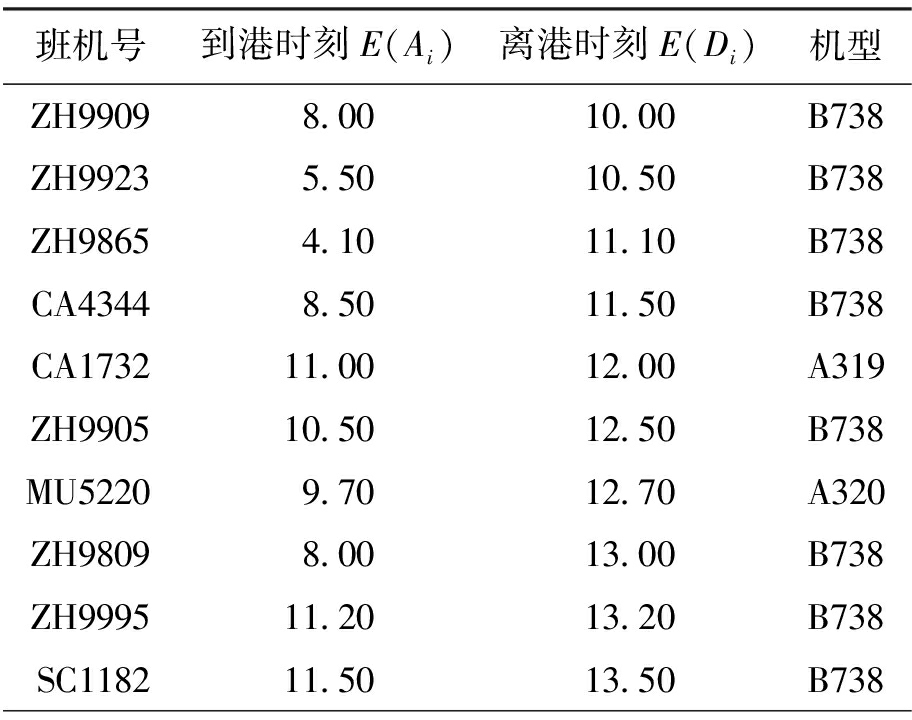
班机号到港时刻E(Ai)离港时刻E(Di)机型ZH99098.0010.00B738ZH99235.5010.50B738ZH98654.1011.10B738CA43448.5011.50B738CA173211.0012.00A319ZH990510.5012.50B738MU52209.7012.70A320ZH98098.0013.00B738ZH999511.2013.20B738SC118211.5013.50B738
表4(续)
Tab.4(Cont)
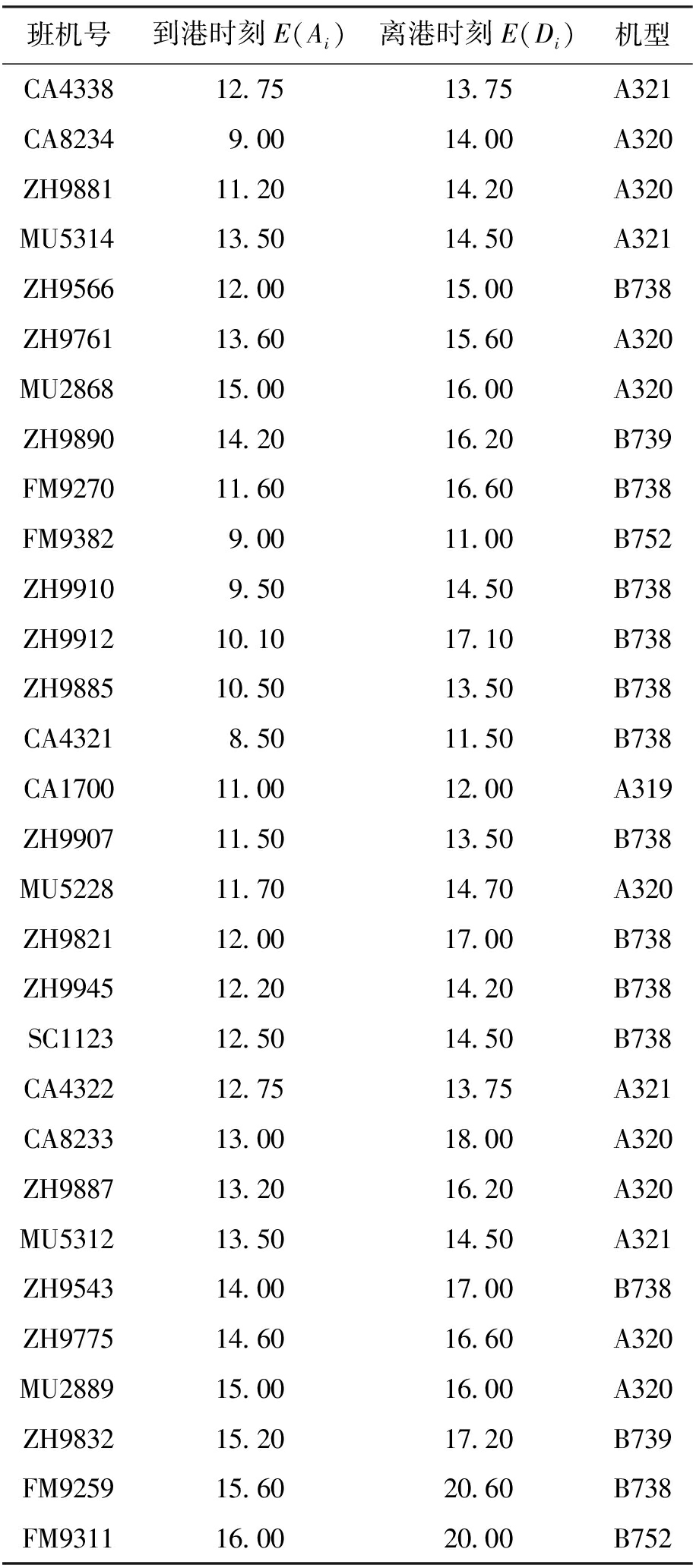
班机号到港时刻E(Ai)离港时刻E(Di)机型CA433812.7513.75A321CA82349.0014.00A320ZH988111.2014.20A320MU531413.5014.50A321ZH956612.0015.00B738ZH976113.6015.60A320MU286815.0016.00A320ZH989014.2016.20B739FM927011.6016.60B738FM93829.0011.00B752ZH99109.5014.50B738ZH991210.1017.10B738ZH988510.5013.50B738CA43218.5011.50B738CA170011.0012.00A319ZH990711.5013.50B738MU522811.7014.70A320ZH982112.0017.00B738ZH994512.2014.20B738SC112312.5014.50B738CA432212.7513.75A321CA823313.0018.00A320ZH988713.2016.20A320MU531213.5014.50A321ZH954314.0017.00B738ZH977514.6016.60A320MU288915.0016.00A320ZH983215.2017.20B739FM925915.6020.60B738FM931116.0020.00B752
模型参数取值与实例一相同,从而得到初始停机位分配方案.使用ILOG软件编写程序得到停机位再分配结果,如表5所示,计算时间为4.187 5 s.由表5可知,在航班规模扩大1倍后,每个停机位调整的班机仍旧最多2个,算法运行时间远远小于1 min,算法在保障尽可能减少调整班机个数的同时又显示了较好的时效性.
本文通过使用多商品网络流模型解决了机场停机位再分配的问题,建立的模型既考虑了机场又兼顾了旅客,实现了机场和旅客双赢的目标.这样既能提高旅客对机场服务的满意度,又能减少机场的运营成本.模型以国内某大型机场停机位的分配方案为基础,利用ILOG优化求解软件得出班机停机位的再分配方案.在不同航班规模的仿真实验中,调整的班机最多为2个,模型求解时间均小于5 s,分配模型显示了较好的实时性和有效性.
表5 停机位再分配方案(实例2)
Tab.5 Gate reassignment scheme (example 2)
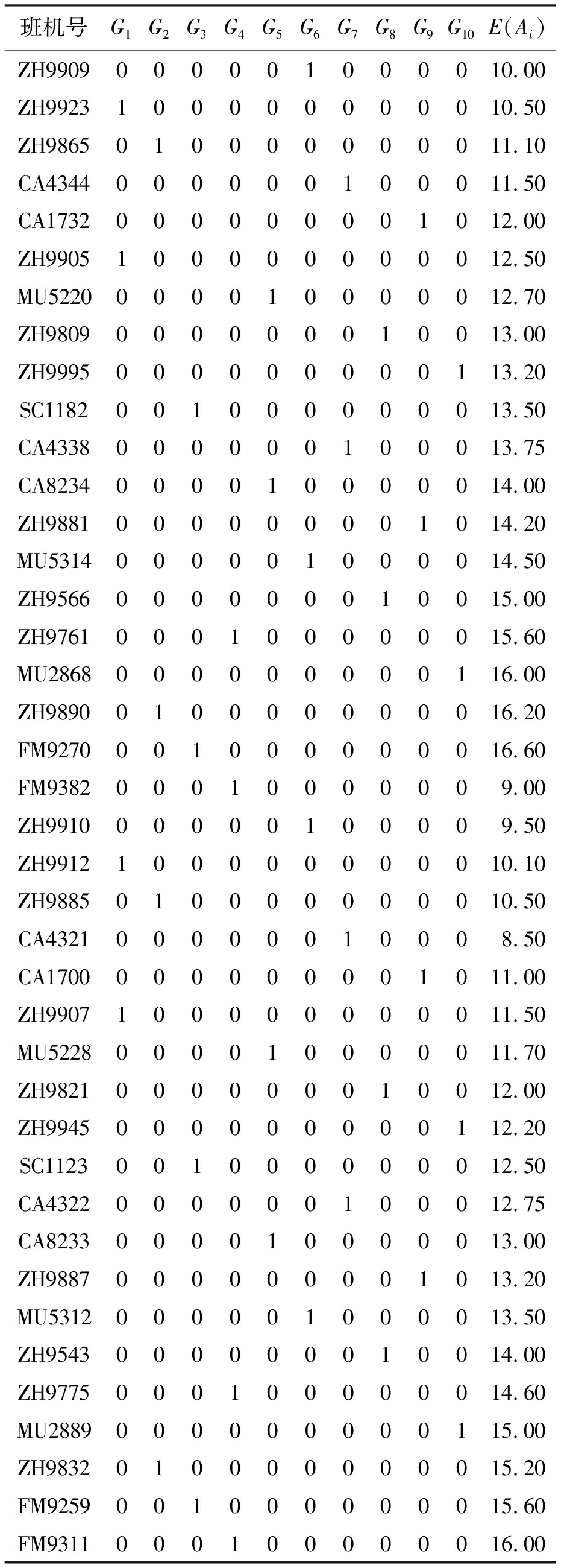
班机号G1G2G3G4G5G6G7G8G9G10E(Ai)ZH9909000001000010.00ZH9923100000000010.50ZH9865010000000011.10CA4344000000100011.50CA1732000000001012.00ZH9905100000000012.50MU5220000010000012.70ZH9809000000010013.00ZH9995000000000113.20SC1182001000000013.50CA4338000000100013.75CA8234000010000014.00ZH9881000000001014.20MU5314000001000014.50ZH9566000000010015.00ZH9761000100000015.60MU2868000000000116.00ZH9890010000000016.20FM9270001000000016.60FM938200010000009.00ZH991000000100009.50ZH9912100000000010.10ZH9885010000000010.50CA432100000010008.50CA1700000000001011.00ZH9907100000000011.50MU5228000010000011.70ZH9821000000010012.00ZH9945000000000112.20SC1123001000000012.50CA4322000000100012.75CA8233000010000013.00ZH9887000000001013.20MU5312000001000013.50ZH9543000000010014.00ZH9775000100000014.60MU2889000000000115.00ZH9832010000000015.20FM9259001000000015.60FM9311000100000016.00
[1] Dorndorf U,Jaehn F,Pesch E.Flight gate assignment and recovery strategies with stochastic arrival and departure times [J].Or Spectrum,2016,39(1):1-29.
[2] 涂浩.基于航班延误成本的停机位分配优化研究 [D].广汉:中国民用航空飞行学院,2017.
(TU Hao.The optimization research of gate assignment based on the flight cost [D].Guanghan:Civil Aviation Flight University of China,2017.)
[3] 陈前,乐美龙.基于安全约束的停机位分配问题的研究 [J].华中师范大学学报(自然科学版),2016,50(1):55-60.
(CHEN Qian,LE Mei-long.Based on the research of security constraints of airpot gate assignment [J].Journal of Central China Normal University (Natural Sciences),2016,50(1):55-60.)
[4] 刘长有,曹强.基于运行安全的停机位再分配问题研究 [J].中国民航大学学报,2014,32(1):15-18.
(LIU Chang-you,CAO Qiang.On gate reassignment for aircraft based on operational safety [J].Journal of Civil Aviation University of China,2014,32(1):15-18.)
[5] Yu C H,Zhang D,Lau H H.A heuristic approach for solving an integrated gate reassignment and taxi sche-duling problem [J].Journal of Air Transport Management,2017,62:189-196.
[6] Wang H,Luo Y,Shi Z.Real-time gate reassignment based on flight delay feature in hub airport [J].Mathe-matical Problems in Engineering,2013(2):11-21.
[7] 李亚玲,李毅.基于可变禁忌长度的优化停机位分配 [J].计算机应用,2016,36(10):2940-2944.
(LI Ya-ling,LI Yi.Aircraft stands assignment optimization based on variable tabu length [J].Journal of Computer Applications,2016,36(10):2940-2944.)
[8] Deng W,Zhao H M,Yang X H,et al.Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment [J].Applied Soft Computing,2017,59:288-302.
[9] 赵伟丽.一种停机位分配问题的网络流数学模型 [J].沈阳理工大学学报,2012,31(4):48-53.
(ZHAO Wei-li.Network flow model and algorithm of gate assignment [J].Journal of Shenyang Ligong University,2012,31(4):48-53.)
[10] Maharjan B,Matis T I.Multi-commodity flow network model of the flight gate assignment problem [J].Computers and Industrial Engineering,2012,63(4):1135-1144.