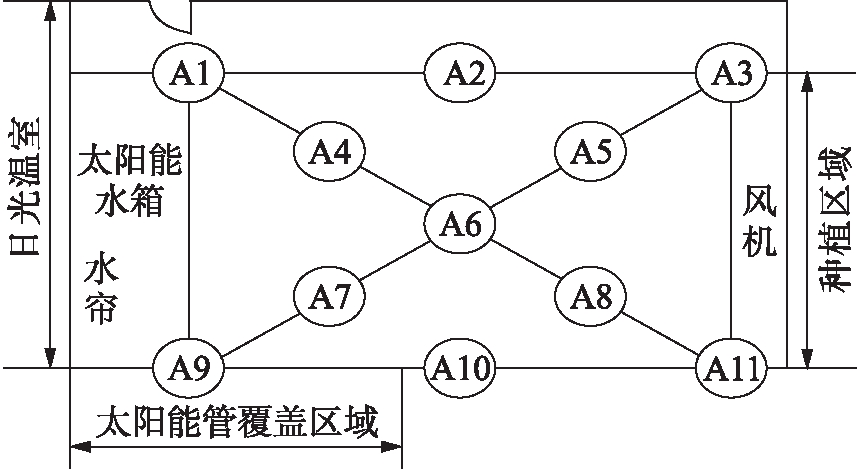
图1 日光温室内传感器布设位置图
Fig.1 Location of sensor layout in sunlight greenhouse
日光温室在我国北方农业生产中占有重要地位,利用传感器采集温度和湿度等数据,可以实时监测并调控生产环境,对节约资源、提高生产效率尤为重要.但是日光温室存在内部构造复杂和环境因子分布不均等问题,合理的传感器布设方案对于保障数据准确度和节省生产成本有着重要意义[1].
多传感器布设问题是目前的研究热点,很多学者对相关问题进行了研究.He等[2]以传感器布设位置的熵值最小化为目标,采用遗传算法研究了输电塔的传感器布设;刘寒冰等[3]基于模态能量评价准则,采用遗传算法研究了桥梁结构传感器的布设;温凯方[4]以三维模态置信准则为优化目标,基于鸽群算法研究了桥梁监测系统传感器的布设问题;张楚旋等[5]构建了传感器布设影响方案的评价指标体系,利用逼近理想解的排序法给出了微震监测传感器的布设方案;孙玉文[6]运用BP神经网络和自适应加权融合算法对农田传感器监测数据进行校准融合,给出了传感器的定位方法;王凡等[7]采用最小二乘法对土壤水分传感器的埋设位置进行了研究;彭秀媛等[8]采用最佳平方逼近最小二乘法给出了日光温室传感器的最佳布设点.
可以看出,目前研究传感器布设的方法主要可以分为两类:一类是基于评价准则,通过智能优化算法、TOPSIS等方法评价给定方案来确定最优方案;另一类是基于监测数据,采用最小二乘估计、数据融合等方法确定传感器布设位置.相对于制定评价准则,基于监测数据分析的方法更加客观易行,更适合日光温室环境内传感器布设.同时,数据融合可以综合考虑多传感器和不同时段的监测数据,比传统的最小二乘估计方法所得结果更准确.
目前,常见的多传感器数据融合方法有神经网络、贝叶斯估计、熵融合和自适应加权融合等.相对于神经网络和贝叶斯等数据融合方法,自适应加权平均融合方法不需要进行概率分析,计算简单,对数据精度要求较低,适用于环境传感器的数据融合.但是传统的自适应加权平均融合算法需要历史观测数据用以计算传感器方差,且适应性不强,无法灵活修改权值.因此,本文将分批估计理论与自适应加权平均融合算法相结合,研究日光温室的传感器布设问题.
首先设计实验方案采集某日光温室内西红柿开花坐果期与结果期生长环境数据;其次基于BP神经网络方法对缺失值进行补全;然后在此基础上对实验数据进行分批估计并进行分段自适应加权平均融合,求取融合值与观测值的相对误差;最后将总误差最小的传感器作为最优传感器,以此为依据确定传感器最佳布设区域.
实验在辽宁省农业科学院用于测试信息化设备的日光温室内进行,温室规格为45 m×9 m,温室内采用基质栽培方式栽培西红柿,行间距1.1 m.降温设备包括放风电机、风机、水帘,降湿设备为放风电机,升温设备包括太阳能、电暖气,冬季生产晚上还会盖上棉被,一般8∶00~16∶00打开棉被,其余时间关闭,如遇雨雪天气则不打开.温度测量采用Sensirion传感器公司的SHT10型数字温度传感器,温度测量范围为-40~+123.8 ℃,测量精度为±0.5 ℃;湿度测量精度为4.5%RH.
目前,常用的日光温室数据采集均采取采样点的方式测量.此次实验的温室是北方常见的矩形温室,为了能够较为全面地检测温室内各点的温湿度情况,选取矩形温室内种植区域的顶点、中心点、各边以及对角线中点等典型位置布设11个监测点.各监测点水平位置一致,如图1所示.实验数据采集时段为2016.09.30~2017.01.18,覆盖冬茬西红柿的开花坐果期与结果期,其中开花坐果期为2016.10.01~2016.10.20,结果期为2016.10.21~2017.01.18,系统设置每隔5 min采样数据1次.本文希望通过分析处理这11个位置的温湿度数据,寻找最佳传感器布设区域,为同类型温室的传感器布设提供合理依据.

图1 日光温室内传感器布设位置图
Fig.1 Location of sensor layout in sunlight greenhouse
传感器在数据采集过程中,由于电压不稳定、操作不当、设备故障等影响因素,可能会短暂处于不稳定状态,造成监测数据的异常或少量缺失,这些异常值或缺失值会极大影响数据连续性以及数据分析处理的准确性,需要加以克服.
温室内温度范围为-10~40 ℃,湿度范围为0~100%RH,首先去掉超出正常值范围的异常数据,接着需要对缺失数据进行补全.本次实验传感器采集的数据具有定距型、样本量大、宏观连续的特点,具有充足的训练样本,适合采用BP神经网络算法预测缺失值.
BP神经网络是一种多层前向型神经网络,权值调整采用反向传播学习算法.BP网络结构包含输入层、隐含层和输出层,各层神经元采用全连接方式.采用BP神经网络进行缺失值预测的关键在于构建网络结构,具体如下:
1) 输入输出层.输入输出层的神经元数量依据样本数据确定,根据本次实验数据特点,确定输入层神经元个数为10,即输入变量为已知10个完整的传感器数据样本;输出层为1,即输出缺失的单个监测数据.
2) 隐含层.采用单个隐含层网络,通过适当增加隐含节点的个数来实现非线性映射.根据隐含神经元个数经验公式(1)来确定神经元个数,然后通过对含不同神经元个数的网络进行训练对比,最后确定隐含神经元个数.
(1)
式中:k为隐含层神经元个数;p为输入层神经元个数;t为输出层神经元个数;m为常数,且1<m<10.本次实验经过测试后确定隐含层神经元个数为11.
2.2.1 数据分批处理
直接采用自适应加权算法需要根据历史数据求得传感器方差,过于依赖历史监测数据,在样本量过大时,方差值发生僵化.分批估计方法将数据分批处理,方差可以根据样本的改变发生变化,有效避免不同监测结果误差所导致的融合结果偏差,从而系统地提高鲁棒性和容错性.因此,本文结合分批估计理论,将多个传感器多次采样结果进行融合处理.
首先对n个传感器将全部数据按照时间段分为若干组,然后对每个传感器各组内的数据做分批处理,步骤如下:
1) 将n个传感器同一时间段的数据组等分成两部分,分别计算其算数平均值和标准差![]()
2) 计算每个传感器该时间段的最小平方误差,其表达式为
(2)
3) 计算每个传感器该时间段的融合值,即
(3)
2.2.2 自适应加权平均融合
设各传感器的加权因子为W1,W2,…,Wn,且![]() 总方差为
总方差为
(4)
数据融合的目标应使总方差最小,即
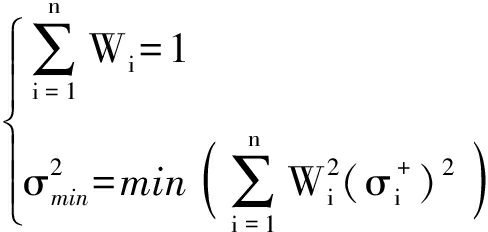
(5)
依据多元函数极值理论,可得
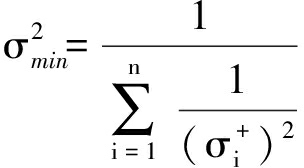
(6)
此时
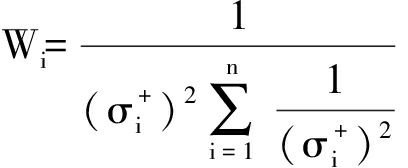
(7)
可得最终融合值为
(8)
3.1.1 缺失值补全
表1为某日11个传感器监测到的7∶00~9∶00的温度数据.日光温室白天会掀去草帘接受太阳光照,在白天受外界影响较大,清晨草帘刚掀开后的一段时间内,室内温度会发生一次较为明显的下降,因为此时太阳出现不久,室外温度仍然低于室内,当草帘掀开后室温下降到室外同一水平,室内温度才开始回升,本组数据恰好为草帘刚掀开时段的温度,因此温度呈明显下降趋势.从表1可以看出,A1缺失8∶52的一组数据.
将A2到A11从7∶02至8∶47时间段的温度数据作为训练输入,A1从7∶02至8∶47时间段的数据作为训练输出.之后将A2到A11在8∶52时间点的数据作为测试输入,A1在8∶52时间点的数据作为测试输出.设定网络的最大学习迭代次数为100次,学习率为0.05,学习精度为0.000 1.该网络模型迭代学习10次完成训练,达到学习精度,预测值为10.984 1 ℃.
表1 神经网络温度训练数据
Tab.1 Temperature training data of neural network ℃
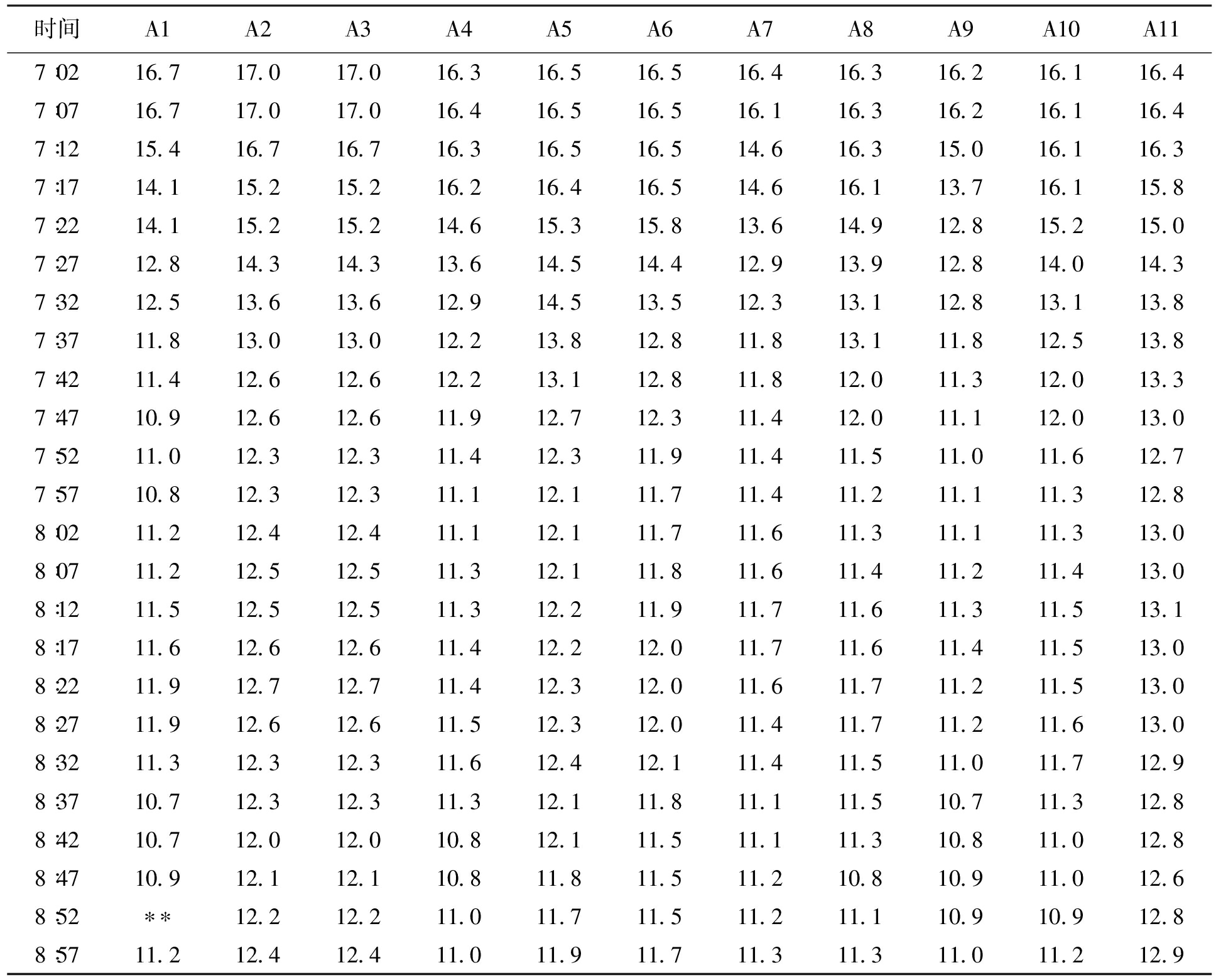
时间A1A2A3A4A5A6A7A8A9A10A117∶0216.717.017.016.316.516.516.416.316.216.116.47∶0716.717.017.016.416.516.516.116.316.216.116.47∶1215.416.716.716.316.516.514.616.315.016.116.37∶1714.115.215.216.216.416.514.616.113.716.115.87∶2214.115.215.214.615.315.813.614.912.815.215.07∶2712.814.314.313.614.514.412.913.912.814.014.37∶3212.513.613.612.914.513.512.313.112.813.113.87∶3711.813.013.012.213.812.811.813.111.812.513.87∶4211.412.612.612.213.112.811.812.011.312.013.37∶4710.912.612.611.912.712.311.412.011.112.013.07∶5211.012.312.311.412.311.911.411.511.011.612.77∶5710.812.312.311.112.111.711.411.211.111.312.88∶0211.212.412.411.112.111.711.611.311.111.313.08∶0711.212.512.511.312.111.811.611.411.211.413.08∶1211.512.512.511.312.211.911.711.611.311.513.18∶1711.612.612.611.412.212.011.711.611.411.513.08∶2211.912.712.711.412.312.011.611.711.211.513.08∶2711.912.612.611.512.312.011.411.711.211.613.08∶3211.312.312.311.612.412.111.411.511.011.712.98∶3710.712.312.311.312.111.811.111.510.711.312.88∶4210.712.012.010.812.111.511.111.310.811.012.88∶4710.912.112.110.811.811.511.210.810.911.012.68∶52∗∗12.212.211.011.711.511.211.110.910.912.88∶5711.212.412.411.011.911.711.311.311.011.212.9
图2为7∶00~9∶00时间段缺失值补全后的温度变化曲线.可以看出,此时温度变化曲线仍然呈连续状态,预测值前后未出现异常,预测结果可以被接受.
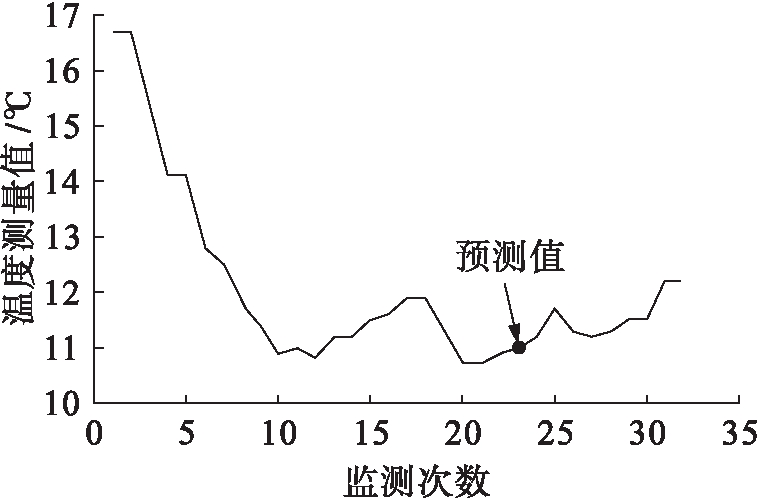
图2 缺失值补全后温度变化曲线
Fig.2 Temperature change curve after complement of missing values
3.1.2 多传感器数据融合
将11个传感器测得的数据按照时间段分为若干组,表2为其中一组,是某日连续11个时间点的温度监测数据样本.
运用式(2)、(3)计算本时段11个传感器的最小平方误差和温度融合值,结果如表3所示.
运用式(6)、(7)计算各传感器的最优权值,结果如表4所示.可得该时段温度最终融合值,即
![]() ℃
℃
同理可得所有时段温度数据和湿度数据的融合值.图3、4分别为某日0时至24时基于分批估计的自适应加权平均融合算法的所有时段温度融合值与湿度融合值.
将基于分批估计的自适应加权平均融合算法、自适应加权平均融合算法和算术平均融合算法的结果进行对比,结果如图5所示.可以看出,三种方法融合后的数据曲线大致趋势保持一致,基本反映了当天温室内温度变化情况,但是在开始阶段和顶点附近融合结果产生较大偏差.在开始阶段,相对于算术平均,基于分批估计的自适应加权平均融合与自适应加权平均融合均能反应数据稳定变化的趋势,较好地弥补了数据突变引起的差异.在曲线顶端,与单纯的自适应加权算法相比,采用分批估计理论对单个传感器分批处理,求得的方差值可以根据样本改变而变化,避免了由于样本量过大产生的方差值僵化.
表2 某时段待融合温度数据
Tab.2 Temperature data to be fused at a certain period ℃
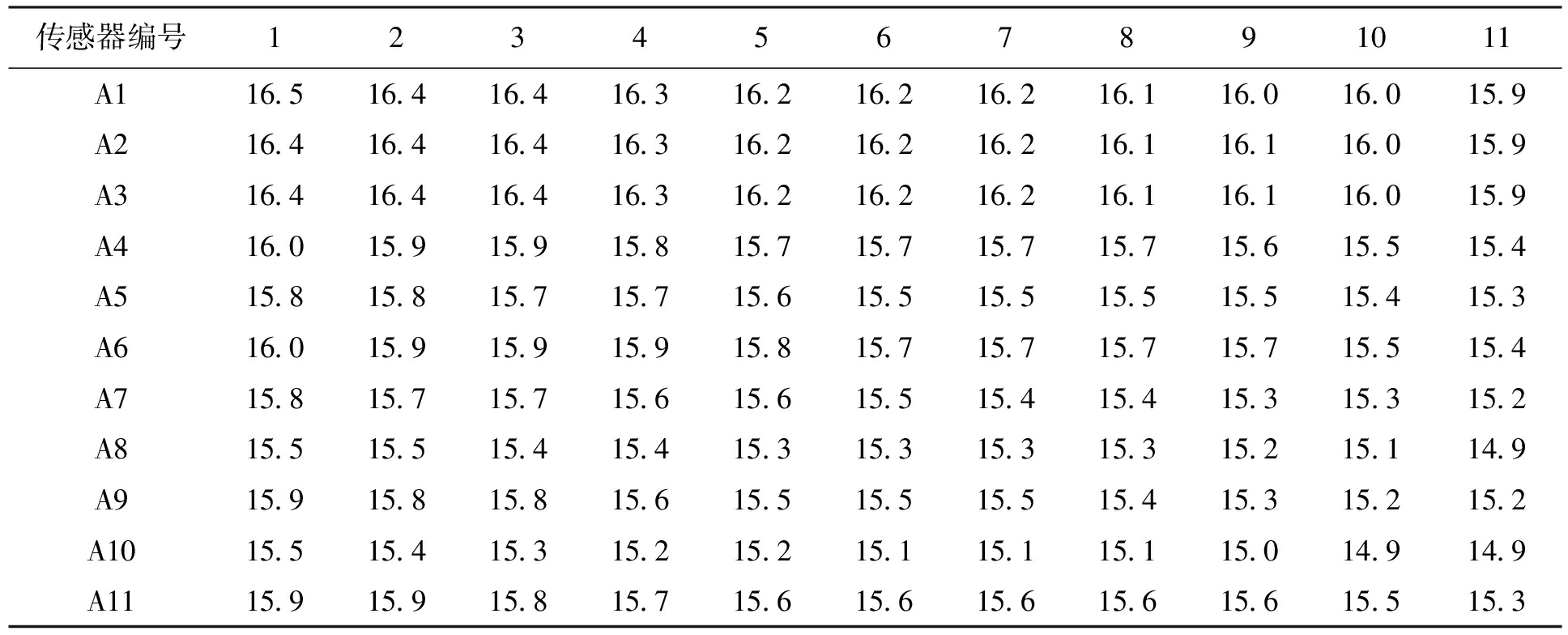
传感器编号1234567891011A116.516.416.416.316.216.216.216.116.016.015.9A216.416.416.416.316.216.216.216.116.116.015.9A316.416.416.416.316.216.216.216.116.116.015.9A416.015.915.915.815.715.715.715.715.615.515.4A515.815.815.715.715.615.515.515.515.515.415.3A616.015.915.915.915.815.715.715.715.715.515.4A715.815.715.715.615.615.515.415.415.315.315.2A815.515.515.415.415.315.315.315.315.215.114.9A915.915.815.815.615.515.515.515.415.315.215.2A1015.515.415.315.215.215.115.115.115.014.914.9A1115.915.915.815.715.615.615.615.615.615.515.3
表3 分批估计的融合值与最小平方误差
Tab.3 Fusion values and variances for batch estimation
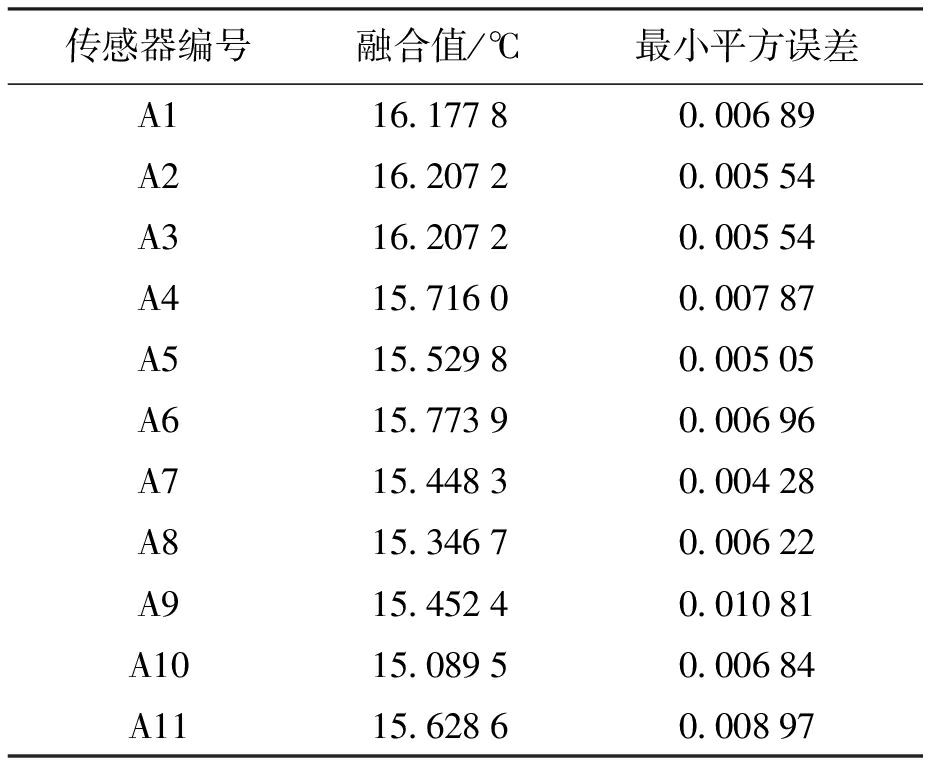
传感器编号融合值/℃最小平方误差A116.17780.00689A216.20720.00554A316.20720.00554A415.71600.00787A515.52980.00505A615.77390.00696A715.44830.00428A815.34670.00622A915.45240.01081A1015.08950.00684A1115.62860.00897
表4 温度传感器最优权值
Tab.4 Optimal weight distribution of temperature sensor
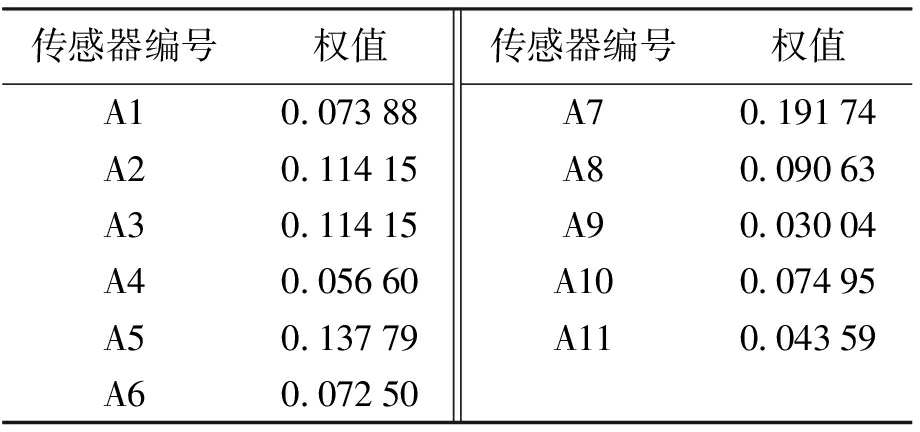
传感器编号权值A10.07388A20.11415A30.11415A40.05660A50.13779A60.07250传感器编号权值A70.19174A80.09063A90.03004A100.07495A110.04359
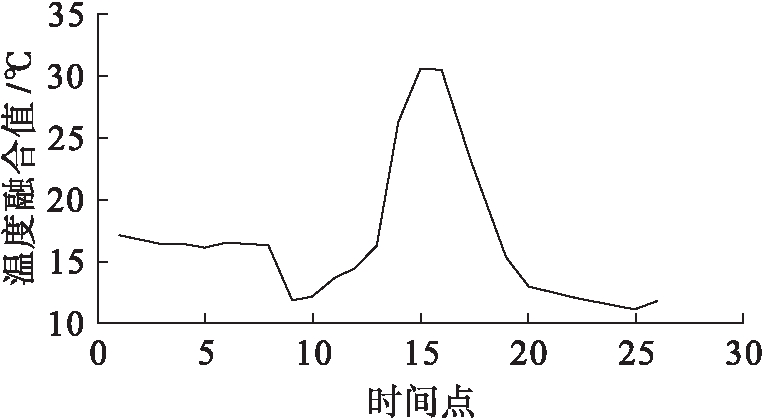
图3 温度融合值
Fig.3 Fusion value of temperature
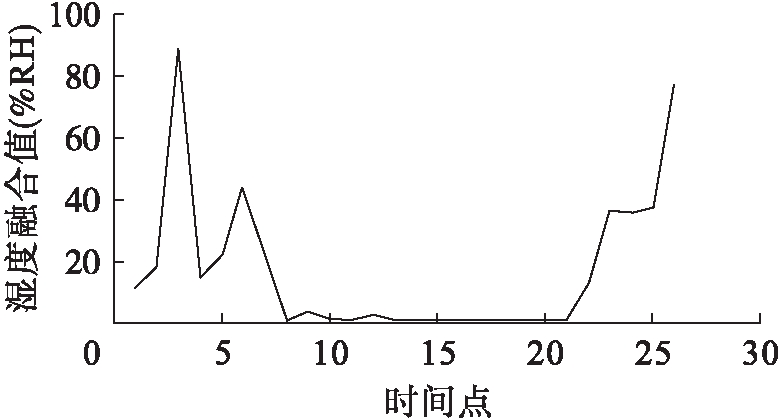
图4 湿度融合值
Fig.4 Fusion value of humidity
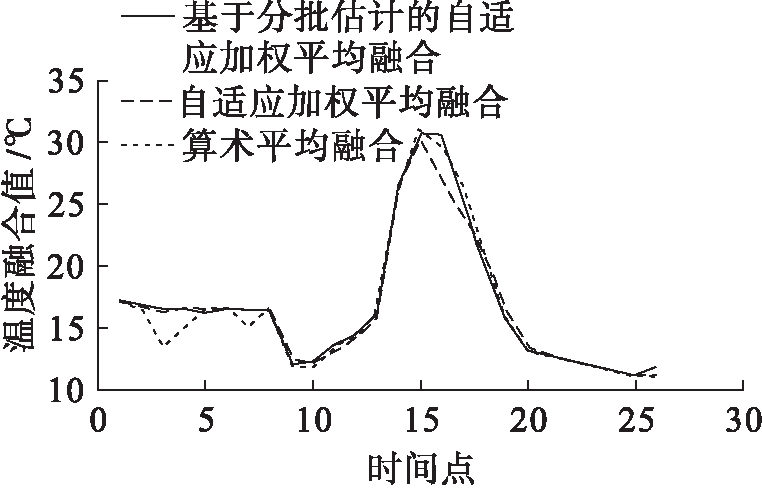
图5 融合结果对比图
Fig.5 Comparison in fusion results
基于求得的温湿度融合值计算融合值与观测值的相对误差,总误差最小的传感器所在区域即为最佳布设区域.根据番茄作物生长周期,将所得监测数据按照开花坐果期与结果期分时段设计布设方案.
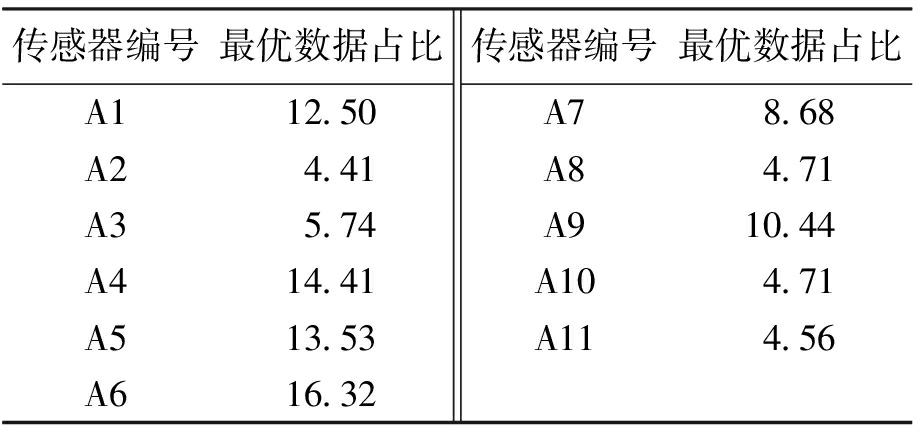
表5、6分别为开花坐果期各温度与湿度传感器所占最优数据的比率.可以看出在开花坐果期,温度总误差最小组占比最大的传感器是A6,但对比其他传感器可以发现,A6所占的16.32%并没有绝对优势,与之相近的分别是A4的14.41%和A5的13.53%,这三个传感器占最优数据比例超过44%.可以认为,温度传感器最佳布设区域应该是A4、A5、A6围成的区域.同理湿度传感器的最佳布设区域应该为A5、A6、A10所在位置区域,最优数据占比和达到51.9%.如果采用温湿度一体传感器,可以选取温度与湿度传感器最佳布设位置的重合区域,可得开花坐果期传感器的最佳布设区域为A5、A6所在区域.
表5 开花坐果期温度传感器最优数据所占比率
Tab.5 Optimum data proportion of temperature sensor during blooming and fruit setting stage %
传感器编号最优数据占比A112.50A24.41A35.74A414.41A513.53A616.32传感器编号最优数据占比A78.68A84.71A910.44A104.71A114.56
表6 开花坐果期湿度传感器最优数据所占比率
Tab.6 Optimum data proportion of humidity sensor during blooming and fruit setting stage %
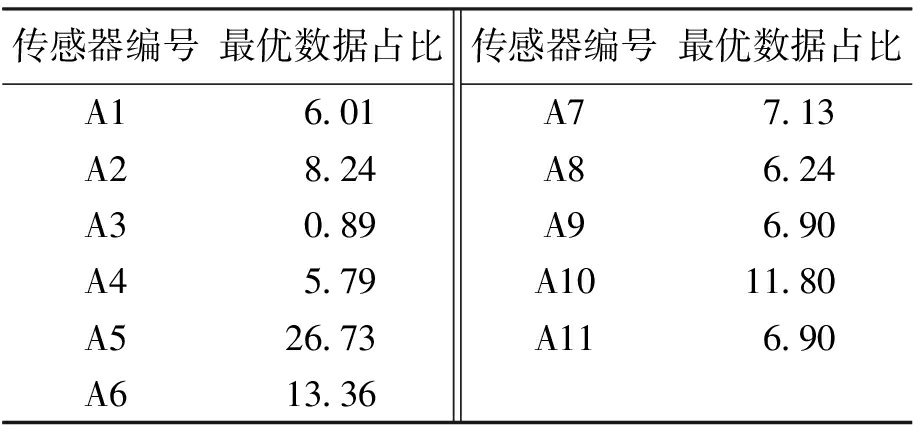
传感器编号最优数据占比A16.01A28.24A30.89A45.79A526.73A613.36传感器编号最优数据占比A77.13A86.24A96.90A1011.80A116.90
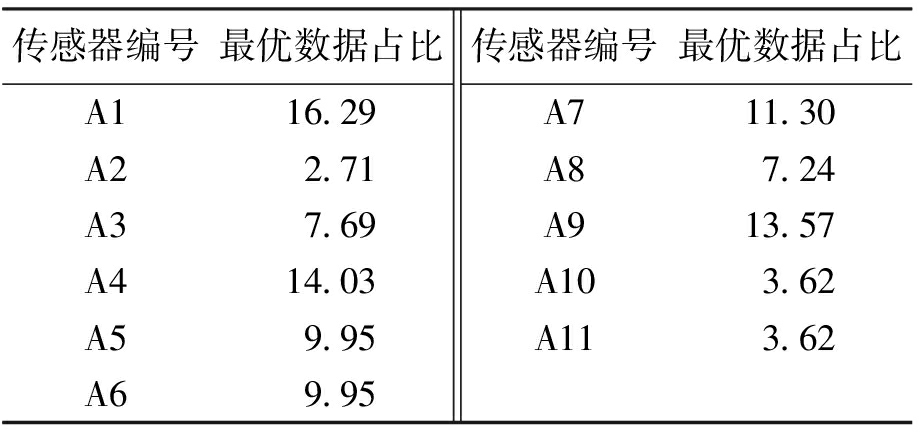
表7、8分别为结果期各温度和湿度传感器所占最优数据的比率.可以看出对于温度传感器最佳布设区域为A1、A4、A7、A9四个传感器所在区域,最优数据占比超过55%;湿度传感器最佳布设区域为A1、A4、A5所在区域,最优数据占比超过51%,综合可得,结果期传感器的最佳布设区域为A1、A4所在区域.结合开花坐果期与结果期分析结果,最终温度和湿度传感器布设方案如图6所示.
最终确定的最优传感器位置并非一个点,而是日光温室几何中心东北侧和西北侧区域.本文不仅考虑了不同生长期的区别,而且给出的布设方案不是单一点,为一个布设区域.因此,本文确定的最优布设位置不仅符合温湿度数据变化稳定、受外界影响较小的特点,而且方便操作人员根据温室内实际情况灵活布设,易于实施.
表7 结果期温度传感器最优数据所占比率
Tab.7 Optimum data proportion of temperature sensor during fruit setting stage %
传感器编号最优数据占比A116.29A22.71A37.69A414.03A59.95A69.95传感器编号最优数据占比A711.30A87.24A913.57A103.62A113.62
表8 结果期湿度传感器最优数据所占比率
Tab.8 Optimum data proportion of humidity sensor during fruit setting stage %
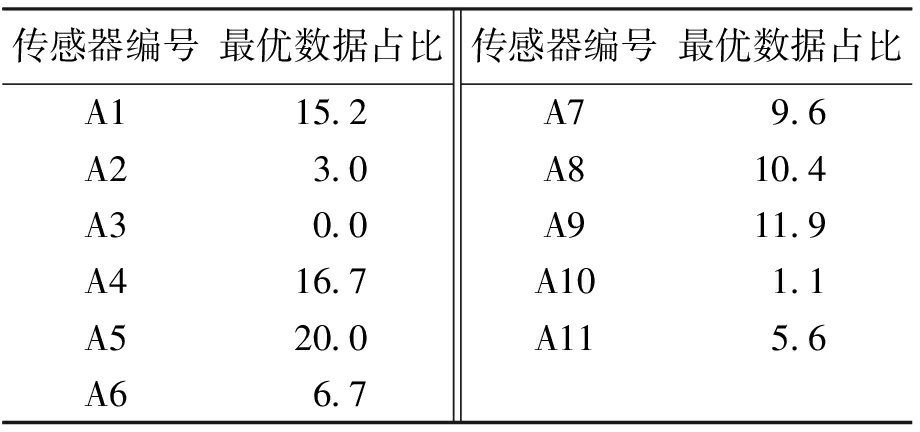
传感器编号最优数据占比A115.2A23.0A30.0A416.7A520.0A66.7传感器编号最优数据占比A79.6A810.4A911.9A101.1A115.6
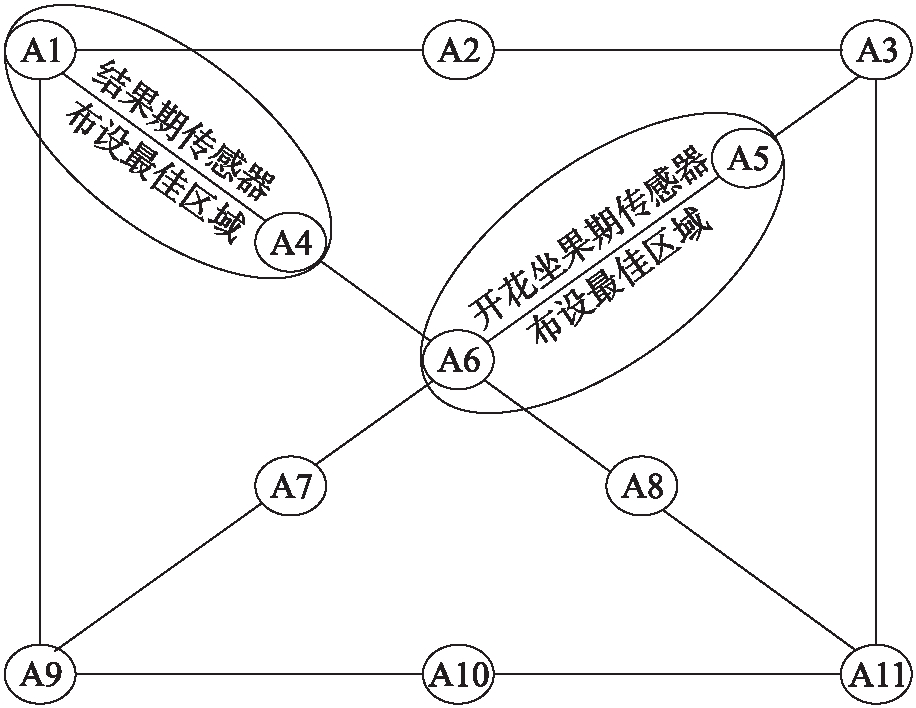
图6 传感器最佳布设区域
Fig.6 Optimal layout area of sensor
本文针对11个观测点测得的西红柿生长湿度数据,首先采用BP神经网络进行缺失值补全,然后采用基于分批估计理论的自适应加权平均融合算法计算出温度融合值,最后通过计算融合值与观测值的绝对误差分别确定了开花坐果期与结果期的传感器最佳布设区域.与一般传感器布设方案只给定单一布设点相比,本文布设方案不仅考虑了不同生长期的区别,而且给出了布设区域,方便操作人员根据温室实际情况进行安装布设,更便于实施.
但是本文只研究了温室内空气温湿度传感器的布设,而温室内影响作物生长的环境因素还包括光照强度、CO2浓度、土壤湿度等因素,下一步应该在综合研究其他温室环境数据的基础上讨论传感器布设方案.
[1] 崔琳.北方日光温室无线传感器多数据融合技术的研究 [D].沈阳:沈阳农业大学,2016.
(CUI Lin.Study on data analysis platform of northern sunlight greenhouse’s monitor and control system [D].Shenyang:Shenyang Agricultural University,2016.)
[2] He L,Lian J,Ma B,et al.Optimal multiaxial sensor placement for modal identification of large structures [J].Structural Control and Health Monitoring,2014,21:61-79.
[3] 刘寒冰,吴春利,程永春.不同适应度函数的遗传算法在桥梁结构传感器布设中的应用 [J].吉林大学学报(工学版),2012,42(1):51-56.
(LIU Han-bing,WU Chun-li,CHENG Yong-chun.Sensor placement on bridge structure based on genetic algorithms with different fitness function [J].Journal of Jilin University(Engineering and Technology Edition),2012,42(1):51-56.)
[4] 温凯方.基于鸽群算法的传感器优化布置方法研究 [D].大连:大连理工大学,2016.
(WEN Kai-fang.Optimal sensor placement based on pigeon colony algorithm(PCA) [D].Dalian:Dalian University of Technology,2016.)
[5] 张楚旋,李夕兵,董陇军,等.微震监测传感器布设方案评价模型及应用 [J].东北大学学报(自然科学版),2016,37(4):594-608.
(ZHANG Chu-xuan,LI Xi-bing,DONG Long-jun,et al.Evaluation model of microseismic monitoring sensor layout scheme and its application [J].Journal of Northeastern University(Natural Science),2016,37(4):594-608.)
[6] 孙玉文.基于无线传感器网络的农田环境监测系统研究与实现 [D].南京:南京农业大学,2013.
(SUN Yu-wen.Research and implementation of field environment monitoring system based on wireless sensor networks [D].Nanjing:Nanjing Agricultural University,2013.)
[7] 王凡,黄磊,吴素萍,等.多路数据采集与处理模型的设计及水分传感器埋设位置优化 [J].农业工程学报,2015,31(21):148-153.
(WANG Fan,HUANG Lei,WU Su-ping,et al.Design of multi-channel data acquisition and processing model and optimization of moisture sensor buried position [J].Transactions of the Chinese Society of Agricultural Engineering,2015,31(21):148-153.)
[8] 彭秀媛,白冰,王枫,等.日光温室内环境科学数据监测传感器的布设 [J].江苏农业科学,2017,45(10):167-170.
(PENG Xiu-yuan,BAI Bing,WANG Feng,et al.Layout of environmental science data monitoring sensors in solar greenhouses [J].Jiangsu Agricultural Sciences,2017,45(10):167-170.)