建筑工程
我国超过一半的面积处于冻土区域，其中多年冻土和季节性冻土占国土面积70%以上，是世界上第三大冻土国家，尤其是我国北部和青藏高原地区分布大量季节性冻土[1].随着“一带一路”战略的进一步实施，基础建设向中亚地区发展，沿线区域工程建设将遇到前所未有的发展良机，工程中遇到的冻融灾害问题应得到更多的关注.
当温度低于0 ℃时，土体中的液相水转化为固相冰，气温回暖后融化，多年循环.在这一过程中由于水分冻融循环过程会引起土体的体积变化，宏观表现为冻胀和融沉，对寒区工程土体有严重危害[2].从内在机理上来看，土体的冻融循环过程是温度场、水分场及力学场相互作用的复杂渗流及热力学综合作用过程[3].
针对这一问题，国内外经过大量理论及试验研究提出了冻胀及融沉理论，并建立了基于温度场、水分场和应力场的耦合方程[4].Harlan[5]认为在冻结过程中，由于热水耦合作用引起水分的迁移，因此建立了水动力模型理论；Konard和Morgenstern[6]引入分凝势概念，提出了水分迁移量和温度梯度的关系.本文基于耦合理论，通过时域差分法建立碾压土本构方程，将冰水相变方程引入耦合方程，分析预测多年冻融循环作用下耦合场变化规律，以此得到水分迁移、应力变化以及位移变化情况，并能预测多年冻融循环下路基沉降以及冻结深度.
寒区道路工程常采用碾压土体作为基层材料，土体经碾压后可以有效降低土体孔隙率，提高土体密实度，进而提高土体强度.因此作为基层材料，为了提高其初始强度，一般都要经过碾压处理.
在寒区的特殊环境下，一方面土体中冰水相变伴随着热量的转移，另一方面含水率的变化会使得土水势变化造成水分迁移，这些温度场和水分场的变化引起重力重分布，往往是导致地质灾害的主要原因.
针对工程土体的环境特点，在冻融循环过程中会引起热、水、力三场耦合作用，因此，本文以连续介质力学和热力学为理论基础，分别建立了三场控制方程.
冻土地区不同于一般地区，环境温度会影响土中冰水相变，因此在建立数学模型时，基于土体非稳态温度场引入了相变方程[7].对于空间中每一点对应一个温度标量T(x，y，z)，冻土相变温度场的温度梯度为
(1)
假定土质分层均匀，质量迁移仅通过液相迁移和冰水相变，采用显热容法对相变区处理建立相变温度场数学模型，即
(2)
C=Csθs+Cwθw+Ciθi+Caθa
(3)
λ=λsλwλiλa
(4)
式中：T为瞬态温度；t为过程进行的时间；λ为导热系数；ρw为水的容重；V为流体的相对速度矢量；C为热容量；Cs、Cw、Ci、Ca分别为土颗粒热容量、水热容量、冰热容量及空气热容量；θs、θw、θi、θa分别为体积土颗粒含量、体积含水量、体积含冰量及体积空气含量；λs、λw、λi、λa分别为土的导热系数、水的导热系数、冰的导热系数及空气的导热系数.
考虑到在土
水体系中，由于热量差异会影响水分的迁移，因此在等温模型上引入非等温扩散流方程，并建立水分迁移模型.本文采用Harlan模型描述冻土水热迁移问题，其中，水分迁移采用渗流Darcy定律[8]，该模型适用于分析冻结区域内水分迁移情况.忽略空气和水蒸气对水分迁移的影响，土介质中的质量迁移方程为
(5)
式中：φ为总水头；ψ为基质热或毛细压力；K为有效导水系数；ΔS为单位时间单位体积冰的变化.
一维稳定或非稳定对流传热的热传导方程为
(6)
(7)
式中：Vx为x方向的液相流速度；
为视容积热容量；ρi为冰的容重；L为潜热(冻或融).
结合总水头计算公式和导热系数计算公式得到Harlan水热耦合模型[9]，即
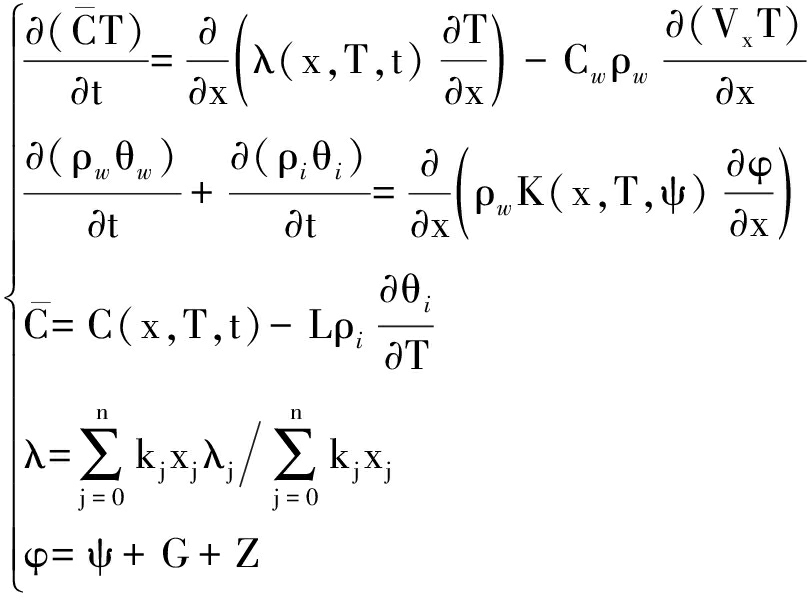
(8)
冻土地区由于温度的改变引起冰水相变，温度场和水分场改变会引起应力场改变.假定土体为均质各项同性，土颗粒和冰、水为不可压缩线弹性变形体，土体基本应力应变方程为
σ=Dε
(9)
式中：σ为应力矩阵；D为刚度矩阵；ε为应变矩阵.
考虑相变的应力场控制方程为
σ=σg+DεV
(10)
式中：σg为由碾压土体自身重力造成的引力；εV为土体冻结膨胀变形.
本构关系包括土体应力应变关系表达式，本文选择Duncan-Chang模型作为冻土基础本构关系，结合温度场、水分场和应力场控制方程，得到耦合场计算模型，即
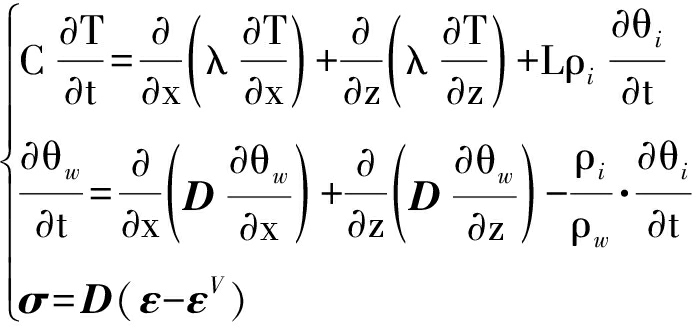
(11)
选取青藏高原某段道路路基作为研究对象，取路基中间竖直方向土体为研究对象，通过耦合模型构建数值计算模型.
研究路段路基填土为粉质黏土及弱风化岩，其参数如表1、2所示.
表1 冰、水热力学参数
Tab.1 Thermomechanics parameters for ice and water
物质C/(kJ·m-3·K-1)λ/(W·m-1·K-1)水41800.602冰19302.220
天然地表的温度计算表达式为
(12)
图1为第1，2，5，10年冬夏温度场分布.根据土层温度分布可知，地表温度随气温迅速降低，由于热传导效应使得浅层土温度剧烈变化，达到一定深度后变化幅度明显减小，原因在于深层土热量补给充分.可以发现在约0 ℃区域相变剧烈，由于耦合作用使得温度传导过程明显减慢，体现于温度场斜率达到0 ℃后明显降低并趋于0.对比第2年、第5年、第10年结果可知，1.0 m深度土层处于相变剧烈区，经过多年冻融循环后趋于一个稳定状态，尤其在第10年出现近1.0 m恒温区，阻碍温度向更深处土层传导.
表2 土热力学参数
Tab.2 Thermomechanics parameters for soil
土层ρd/(kg·m-3)λ-/(W·m-1·K-1)C-/(kJ·m-3·K-1)λ+/(W·m-1·K-1)C+/(kJ·m-3·K-1)路基填土20001.98010060.3461006黏土19201.35118791.1252357弱风化岩20001.82418461.4742099
注：ρd为土体干密度；+、-分别为对应土层的上下表层。
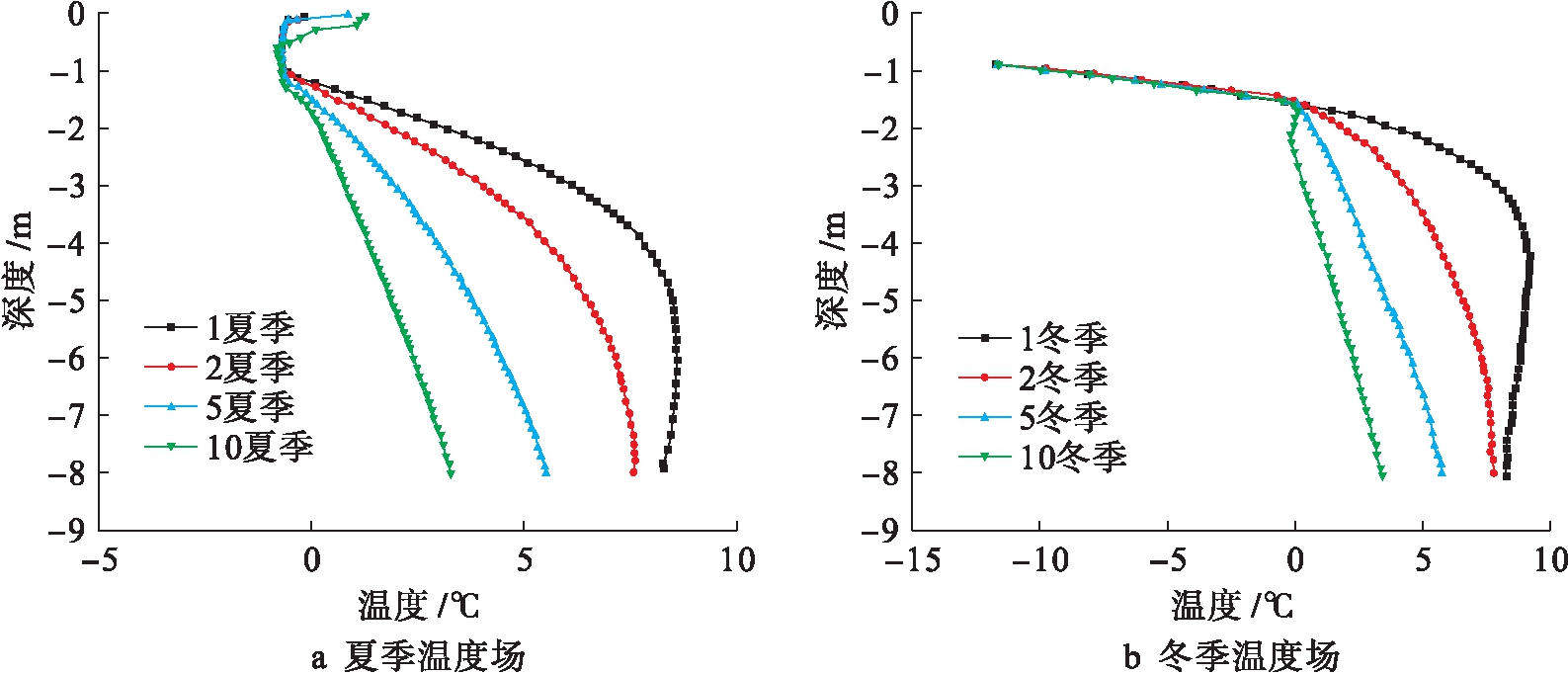
图1 第1，2，5，10年冬夏温度场分布
Fig.1 Distribution of temperature field in summer and winter in year of 1，2，5 and 10
图2为1 m深度处温度变化.取深度1 m土温度变化为研究对象，可知在冬季(冻融循环过程)出现温度变化放缓区，随着冻融循环过程不断重复，这一区域的温度场趋于一个稳定值，温度变化不再明显.
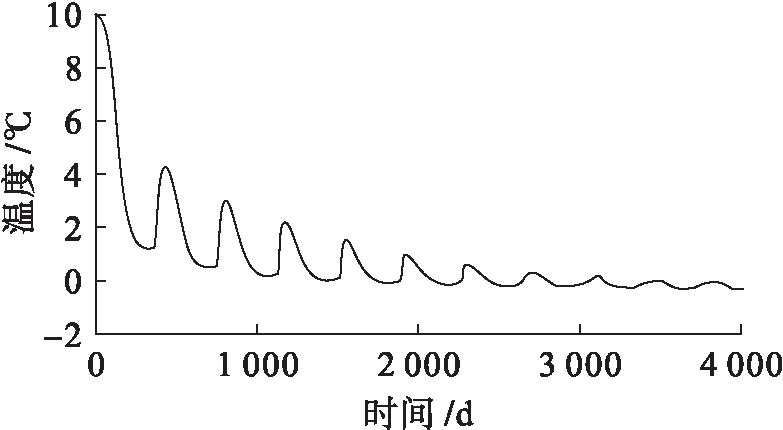
图2 1 m深度处温度变化
Fig.2 Temperature variation at depth of 1 m
图3为第2，5，10年冬夏含水量分布.根据水分场分布可知，土层中水分在一定深度处急剧变化，这一深度与温度场所反应出的相变剧烈区相对应，随着冻融循环过程的往复，这一聚变区不断加深并扩张[10].表层土得到补给，含水量变化明显，深层土与温度场相似，达到一定深度区域稳定值后，并不会因表层或相变引起水分波动而变化.
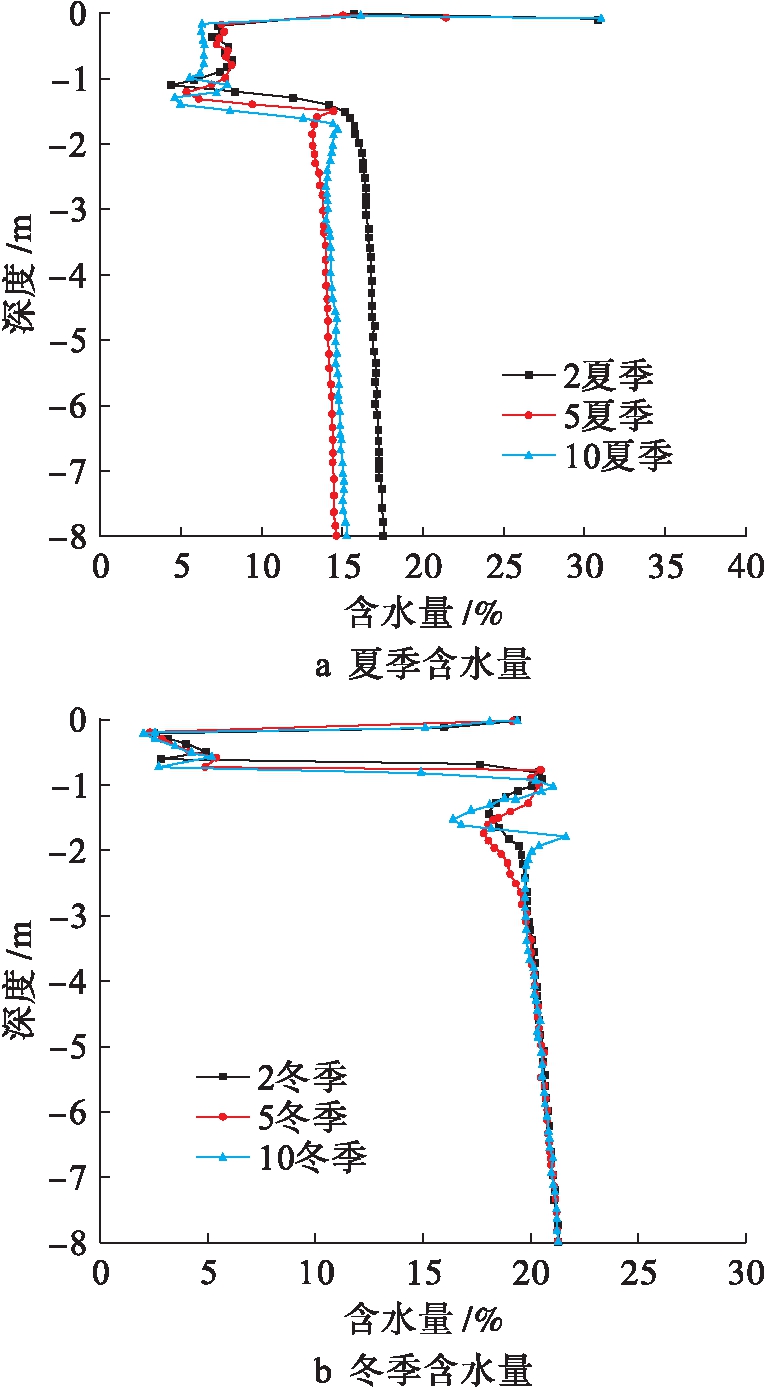
图3 第2，5，10年冬夏含水量分布
Fig.3 Distribution of water content in summer and winter in year of 2，5 and 10
图4、5为1、2 m深度处含水量变化.对比1、2 m深度土层水分场可知，1 m深度水分场呈现明显的周期性特点，当超过2 m后周期性特点明显降低，耦合作用效果降低，水分场波动多来源于水分补给或土层因素.
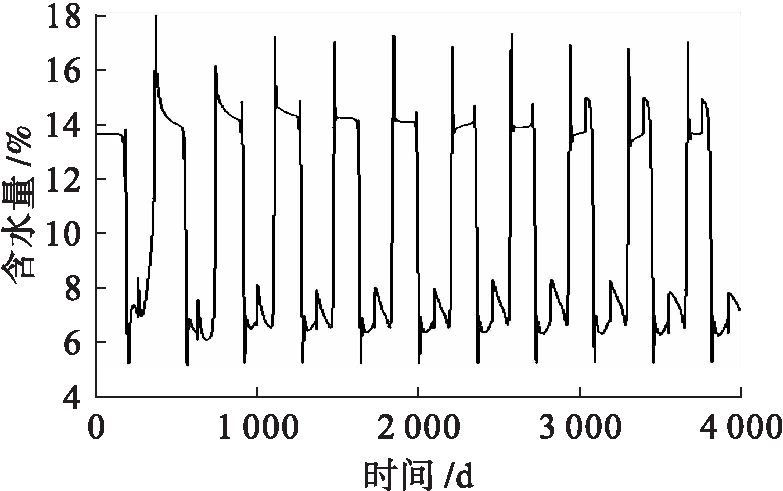
图4 1 m深度处含水量变化
Fig.4 Variation of water content at depth of 1 m
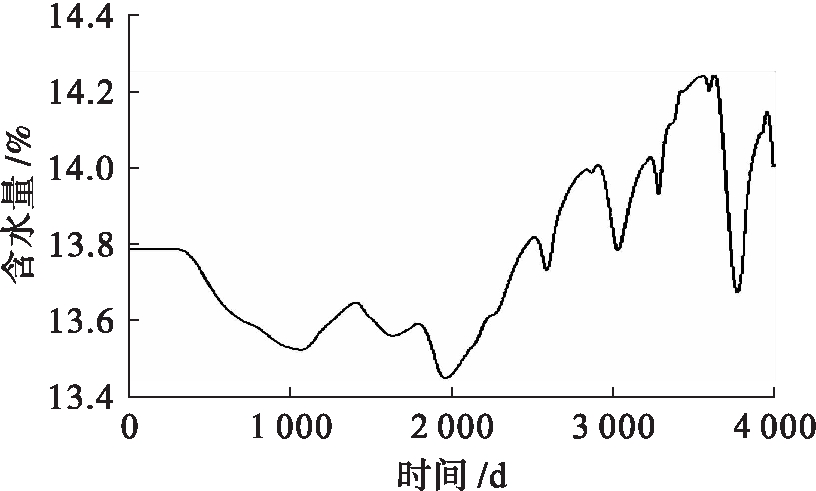
图5 2 m深度处含水量变化
Fig.5 Variation of water content at depth of 2 m
图6为第2，5，10年冬夏应力增量场.对比应力增量可知，土层冻结区域出现一个峰值，由于土层中多场耦合及温度变化引起相变和水分场变化，通过冻结力与应力场产生耦合作用，造成了冻结区的应力峰值.随着多年冻融循环，应力增量仅表现在冻结区，对深处土层影响减弱，与温度场和水分场变化协调，符合工程实际.
通过上述计算可以得到土层的位移和冻结深度变化，如图7、8所示.随着冻结次数增加，冻结深度有所增加，在达到第六次冻结后冻结深度不再发生变化，即冻结循环过程趋于稳定.在本次计算中，最大冻结深度可达到1.8 m.
由图7可知，正值表示地基表面升高，负值表示低于初始值，初始状态为第一年冬天.随着温度降低，土体冻结导致体积膨胀，地基表层出现隆起.随着固相冰向液相转化，土体表面下沉，即融沉效应，同时浅层土体融化的液相水会导致局部水分增加，减弱土体有效应力，加剧融沉，因此，土体下沉常表现为短时间急剧下降.随着时间增加，冻融循环作用往复，形成较为稳定的冻结带，融沉深度趋于稳定.由于冻结深度缓慢加深，冻胀作用随之不断增加，长期来看对于道路工程是一种危害.
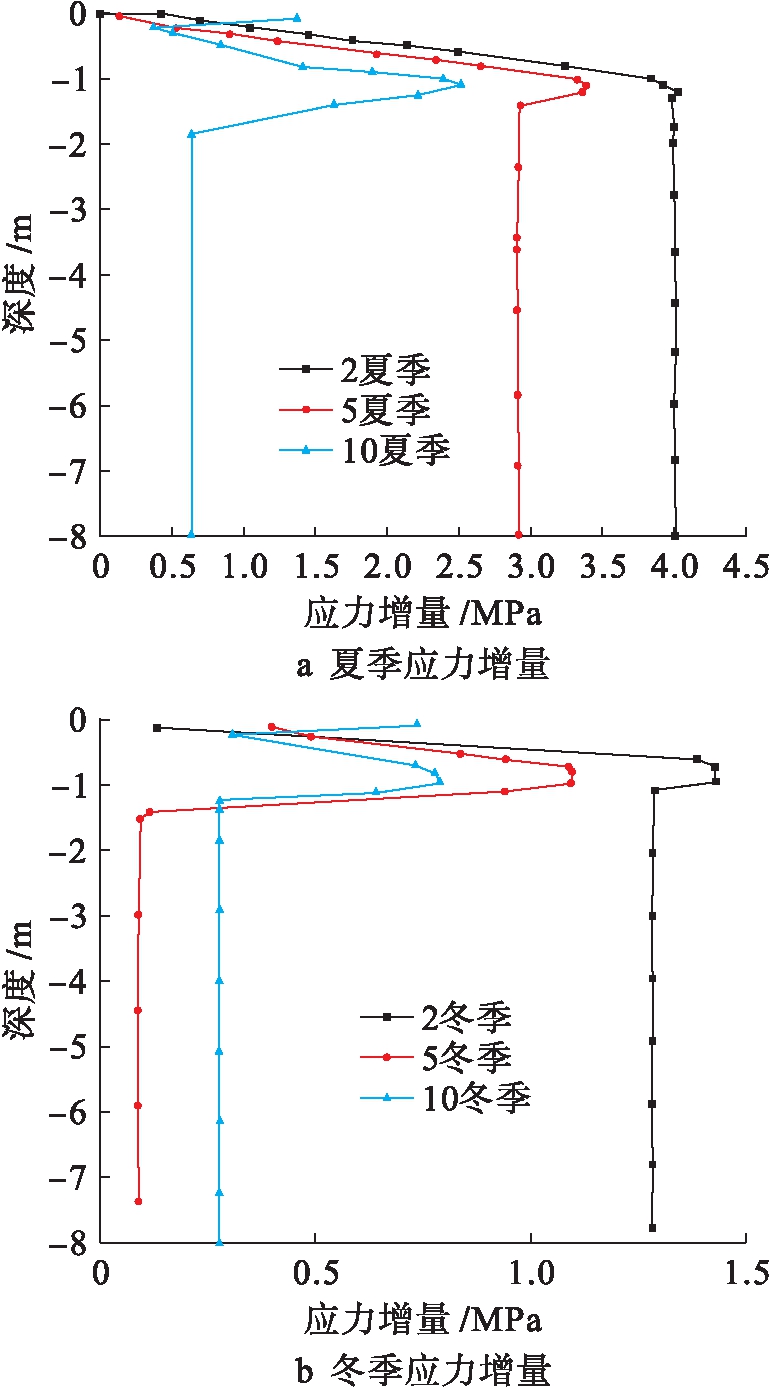
图6 第2，5，10年冬夏应力增量场
Fig.6 Stress increment field in summer and winter in year of 2，5 and 10
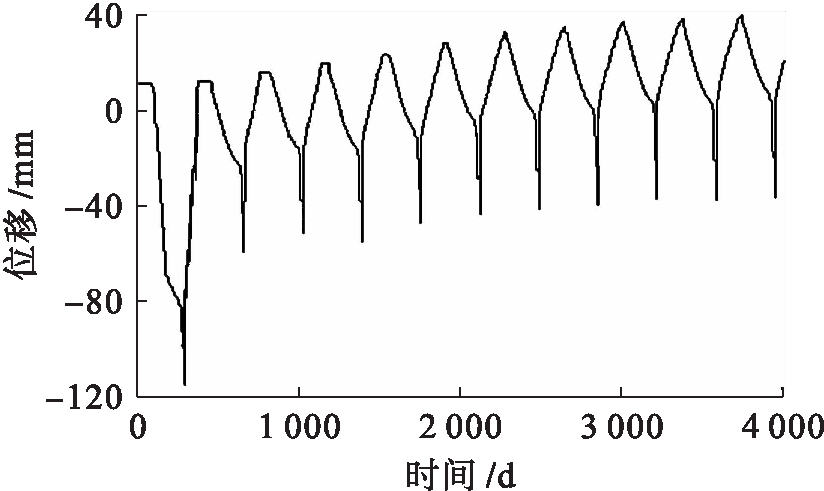
图7 路基表面位移变化
Fig.7 Variation of surface displacement of highway foundation
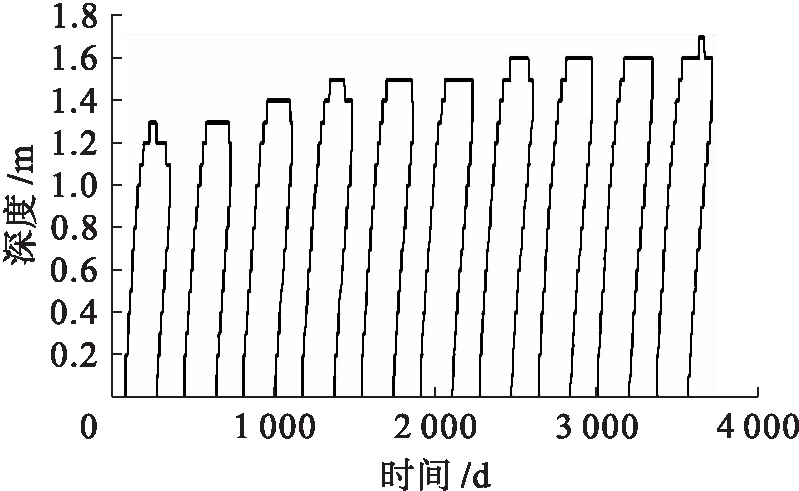
图8 冻结深度变化
Fig.8 Variation of frozen depth
本文基于Duncan-Chang模型，考虑温度场、水分场以及应力场耦合条件建立了寒区冻土的控制方程.通过时域差分法，选取研究实例，对多年往复冻融循环进行计算模拟，得到以下结论：
1) 在冻融循环过程中，温度场、水分场以及应力场呈现明显的周期性变化规律，表现为温度变化冰水相变体积变化.其中，温度场是决定冰水相变的重要因素，相变所引起的体积变化和水土势变化分别引起应力场和水分场变化，同时水分和体积变化对于土体温度变化和分布也有重要的影响.本文通过耦合方程模拟三场变化规律，能够真实地反映土体的变化规律，具有较高的可信度.
2) 本文在一维条件下将碾压土体分层，通过时域差分法建立耦合计算模型，得到三场分布及变化规律，模型条件和结果符合实际情况.该计算模型能够在一定精度下简化计算过程，具有较高的计算效率.
3) 计算模型精确预测了土层剧烈应变区域以及冻结深度，与实际变化规律一致，可用于对土层分析预测.本文结果反映了温度场、水分场和应力场的紧密耦合关系，尤其是在明显的相变剧烈区域.
[1] 陈卫忠，谭贤君，于洪丹，等.低温及冻融环境下岩体热，水，力特性研究进展与思考 [J].岩石力学与工程学报，2011，30(7)：1318-1336.
(CHEN Wei-zhong，TAN Xian-jun，YU Hong-dan，et al.Advance and review on thermo-hydro-mechanical characteristics of rock mass under condition of low temperature and freeze-thaw cycles [J].Chinese Journal of Rock Mechanics and Engineering，2011，30(7)：1318-1336.)
[2] 周扬，周国庆.土体一维冻结问题温度场半解析解 [J].岩土力学，2011，32(增刊1)：309-313.
(ZHOU Yang，ZHOU Guo-qing.Semi-analytical solution for temperature field of one-dimensionalsoil free-zing problem [J].Rock and Soil Mechanics，2011，32(Sup1)：309-313.)
[3] 齐吉琳，马巍.冻土的力学性质及研究现状 [J].岩土力学，2010，31(1)：133-143.
(QI Ji-lin，MA Wei.State-of-art of research on mechanical properties of frozen soils [J].Rock and Soil Mechanics，2010，31(1)：133-143.)
[4] 周扬，周国庆.土壤冻结水热耦合有限容积模拟研究 [J].岩土工程学报，2010，32(3)：440-446.
(ZHOU Yang，ZHOU Guo-qing.Finite volume simula-tion for coupled moisture and heat transfer during soil freezing [J].Chinese Journal of Geotechnical Engineering，2010，32(3)：440-446.)
[5] Harlan R L.Analysis of coupled heat-fluid transport in partially frozen soil [J].Water Resources Research，1973，9：1314-1323.
[6] Konrad J M，Morgenstern N R.A mechanistic theory of ice lens formation in fine-grained soils [J].Canadian Geotechnical J，1980，17：473-486.
[7] 张玉军.模拟冻融过程的热水应力耦合模型及数值分析 [J].固体力学学报，2009，30(4)：409-415.
(ZHANG Yu-jun.Coupled thermo-hydro-mechanical model and numerical analysis for simulation of freezing-thawing process [J].Chinese Journal of Solid Mechanics，2009，30(4)：409-415.)
[8] 孙海霞，张科，陈四利，等.考虑降水影响与分布开挖的基坑变形数值模拟 [J].沈阳工业大学学报，2014，36(6)：711-715.
(SUN Hai-xia，ZHANG Ke，CHEN Si-li，et al.Nume-rical simulation on behavior of foundation pit deforma-tion with considering dewatering and multi-stage exca-vation [J].Journal of Shenyang University of Techno-logy，2014，36(6)：711-715.)
[9] 汪智慧.地基土的超固结特性对浅层平板载荷试验的影响 [J].沈阳工业大学学报，2017，39(2)：225-229.
(WANG Zhi-hui.Effect of over-consolidation characteristics of foundation soil on shallow plate loading test [J].Journal of Shenyang University of Technology，2017，39(2)：225-229.)
[10] 刘建军，谢军.岛状多年冻土管道周围热水应力耦合数值模拟 [J].岩土力学，2013,34(增刊1)：444-449.
(LIU Jian-jun，XIE Jun.Numerical simulation of thermo-hydro-mechanical coupling around underground pipelines in patchy permafrost region [J].Rock and Soil Mechanics，2013，34(Sup1)：444-449.)