雅克比方程得到最优时间路径，改进后向路径追踪的数值计算精度保证了规划路径的可行性.仿真结果表明，算法可以有效应对复杂的有向外力场，并且在强外力场中仍保持路径的可行性.采用的连续路径规划方法可以突破传统机器人路径规划算法基于格点搜索的限制，并有效利用空间中存在的外力场.摘 要： 针对有向外力场作用下基于格点的机器人路径规划方法不能得到最优解的问题，采用了基于水平集方法的路径规划方法.将机器人的粒子跟踪转变为曲线的数值演化，通过解哈密尔顿雅克比方程得到最优时间路径，改进后向路径追踪的数值计算精度保证了规划路径的可行性.仿真结果表明，算法可以有效应对复杂的有向外力场，并且在强外力场中仍保持路径的可行性.采用的连续路径规划方法可以突破传统机器人路径规划算法基于格点搜索的限制，并有效利用空间中存在的外力场.
机器人路径规划问题一直是研究的热点，在移动机器人[1]、水面舰艇[2]、水下机器人[3]以及物流运输[4]等领域有着许多研究成果.传统的地面机器人路径规划侧重于分析障碍物或者危险区域来保证机器人的安全，同时使得路径最短.在一些新的应用场景中，如轻量级旋翼无人机在风场中或者水下机器人在流场中运行，机器人的行为明显受到空间内有向外力的影响，这种有向外力会对机器人的行为起到促进或阻碍的作用.因此机器人在路径规划时需要考虑外力存在的情况，合理利用外力对机器人的某项指标进行优化.
Garau等[3]利用A*算法获得能耗最优的AUV路径；崔宝侠等[5]将A*算法的搜索领域从8个扩展到了24个，使得规划出的路径更短且更光滑；崔宝侠等[6]采用人工势场方法提高了机器人在恶劣环境下的适应性；Rhoads等[7]通过间接求解哈密顿雅各比贝尔曼方程，并结合使用了欧拉拉格朗日方程(含边界点)的反馈控制率来不断迭代极值曲线场，最终求得机器人的时间最优路径.
Petres等[8]提出了一种基于快速行进算法的连续路径规划方法，方法定义了各向异性的代价函数，其中环境中的有向外力场作为优化问题的约束条件.该方法是有向外力场作用下机器人基于网格点的路径规划方法的突破，但仍存在很大的问题，主要在于它只适用于线性代价函数，导致在过强的外力场中无法规划出可行的路径.Lolla等[9]提出了海洋环境中在流场影响下的水下机器人路径规划问题，突破了路径规划问题基于格点搜索的限制，并且在理论上保证了在强海流中路径的可行性.但是由于在计算机中数值计算还是采用离散化的方式，所以受到数值方法的约束，在实际强海流中路径的可行性并没有得到保证.
本文有以下两点贡献：首先是通过重新定义问题，将海流的情况推广到有向外力的作用情况，使得方法有更广泛的意义；另外是改进了数值方法，使得在强外力作用下，规划出路径的可行程度更高.
给定一个配置空间Ω={Ωx，Ωy}，空间中点的定义为X.空间中存在着有向外力引起的速度场Vf={Vfx，Vfy}，路径规划方法要在起始点Xs和目标点Xf之间找到一条路径.定义该路径γ在t时刻穿过点X满足微分方程
其中，u决定了路径γ形状将如何变化.在机器人的路径规划问题中，u可以视作对机器人控制率，方法的目的是要找出能够形成最优路径γ*的最优控制率u*.定义机器人在有向外力作用下的单步移动代价函数为L(X，u)≥0，则沿着路径γ运动所付出的总代价为
J(γ)=
L(X(τ)，u(τ))dτ
(1)
J(γ)是一个泛函函数，因为J(γ)是γ的函数，而γ又是t的函数，则最优路径可以定义为γ*=
最优总代价函数可以写为
L(X*(τ)，u*(τ))dτ
(2)
在机器人学中，一个基本的路径规划问题，也被称作为“泽梅洛导航问题”，可以描述为找到一条在最短时间内从起始点到目标点的路径，即时间最优路径.假设L(X，u)=1，则J(γ)=
dτ=t，即为机器人行驶的时间.机器人在有向速度场中的运动可以描述为
其中，vn为机器人的速度；m为一个单位向量，即
为t时刻X点的速度场.
该模型不考虑机器人具体的动力学，在机器人的运动空间远远大于机器人尺寸的应用场景中，这种规约是完全合理的.在机器人本体更高层面上做规划有着非常重要的现实意义，本文也将在这个层面展开对问题的阐述.
水平集方法的思想起源于曲线演化理论，但和曲线演化理论相比，其克服了曲线演化理论的缺点，适用范围更大.曲线演化问题可以描述为：在二维欧式空间R2中的一条光滑闭合曲线沿着其法线方向以一定速度运动，形成以时间为变量的一簇曲线的过程.假设C=C(p)是一条光滑封闭的曲线，p是任意的参数化变量，设E为切线，N为法线，则存在如下关系：
其中，α和β分别为速度函数在切线方向和法线方向的分量.由于曲线在切线方向上的运动仅仅影响曲线的参数化，不会改变曲线的形状和几何属性.根据曲线演化定理机制，对于任何的速度函数(α，β)总是存在对应的
以保证曲线上的最终演化结果是相同的，因此在具体实现时可以只考虑曲线演化在法线上的运动，演化示意图如图1所示.曲线演化方程可以改写为
=HN
(3)
式中，H为速度函数.
经过一段时间的演化后，曲线可能发生拓扑结构变化(例如断裂或者合并等).曲线演化一般会涉及到曲线的参数化，而曲线参数化最大的缺点就是不易于计算曲率、法向矢量等曲线几何参数，且难以处理曲线的拓扑结构变化.
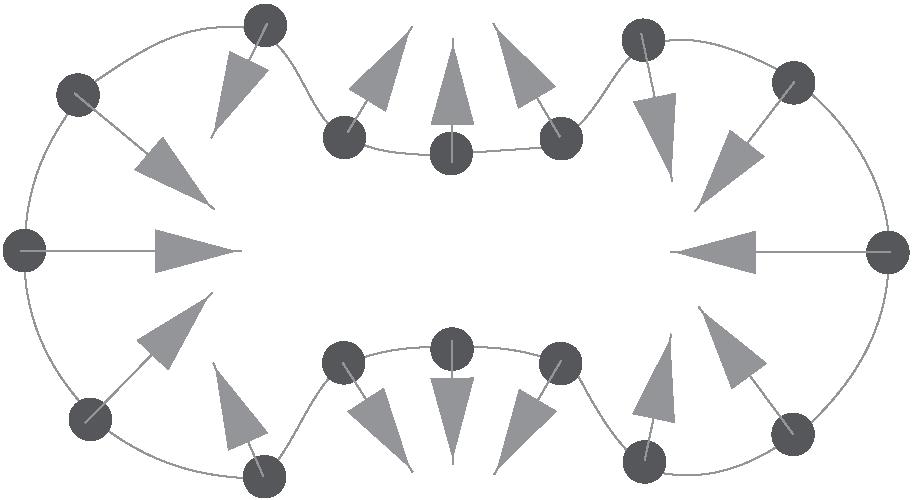
图1 曲线按法线方向的演化示意图
Fig.1 Schematic evolution of curvealong normal direction
水平集方法是一种用于界面跟踪和形状建模的数值方法，其最大的优点是可以在笛卡尔网格中对演化的曲线(面)进行数值计算，而不必对曲线(面)进行计算；水平集方法一个重要的理论前提是隐函数的概念，在曲线演化理论中引入水平集的目的就是为曲线提供一种隐式表达方式，从而避免参数化这种显式表达所带来的一系列问题.其主要思想是，将移动变形的曲面嵌入到高一维的函数中，即将曲线的拓扑结构变化表示成一个连续变化的曲面与一个固定的平面(如高度为零的平面)的交线变化，曲面本身可以不发生拓扑结构的变化，从而使得复杂的曲线运动过程变为高维函数的演化过程.
高维曲面φ选取应该是越简单越好，如果该曲面和某一简单的函数之间为一一对应的关系，则选取这种简单的函数来替代“高维曲面”.在水平集问题中，φ通常被选取为“符号距离函数”.假设要跟踪曲线(即零水平集)为∂ω，距离函数d(X)为曲线外围或内部某点到曲线的最短距离，在计算机计算过程中，∂ω本身是由一系列的离散点组成的，所以d(X)的数学表述为d(X)=min|X-Xi|，其中，Xi为组成∂ω的所有点.符号距离函数定义为
(4)
对于∂ω上的所有点Xi均有φ(Xi)=0，选取这种“符号距离函数”作为“高维曲面”存在诸多好处.首先它是光滑曲线，可以避免等高线上出现很陡的梯度，便于后面的计算使用.φ(X)是和时间相关的，所以可被写作φ(X，t)，又因为其包含封闭曲线C，所以也可写作φ(C(t)，t)，简写为φ.
对于t时刻，演化得到的曲线C(t)和零水平集φ(C(t)，t)=0相等，将其对时间求导可得
+
(5)
在微分几何中，曲线或曲面上的内单位法线和梯度关系为
(6)
由此可见梯度和法线方向一致，将式(5)、(6)联立可得
=-φHN=-H|φ|
(7)
考虑路径γ(t)=X，则φ沿着γ的变化满足
对于零水平集，即
0，则有
其中，
为机器人自身的运动速度，与曲线扩张法线的方向一致.结合式(6)则有
满足哈密尔顿雅克比方程，即
φ(X，t)=0
(8)
假设零水平集在初始时刻为一条极小的封闭曲线，即该曲线所包含的面积趋近于0，但可以保证在曲线上每一点上的法向存在，则式(8)初始条件为
(9)
式中，
为第二类范数，即欧几里得距离.
在t=0时，零水平集φ(X，t)=0，即为机器人的出发点，然后曲线按式(8)由该起点开始随着时间向外演化.对于任意一点y，零水平集曲线第一次与其相遇的时间为T(y)，则有φ(y，T(y))=0.当φ(d，T(d))=0或
(即演化超时)时，演化过程结束.
由于T(y)时刻的零水平集是由t=0时刻演化所得，所以如果将T(y)时刻位置看作与y重合，则可以得到上一时刻的位置，按此思路可以逆推出t=0时刻的位置就是出发点.反向路径逆推过程满足
(10)
将所有这些逆推得到的点相连，即可得到路径γ，可以发现T(y)刚好是从起点到终点所需的时间.
算法总共分为两部分，分别称为前向零水平集演化和后向路径追踪.
定义四个差分算子，分别为x方向和y方向上的向前差分和向后差分，对应着连续x和y方向上的偏导数，即
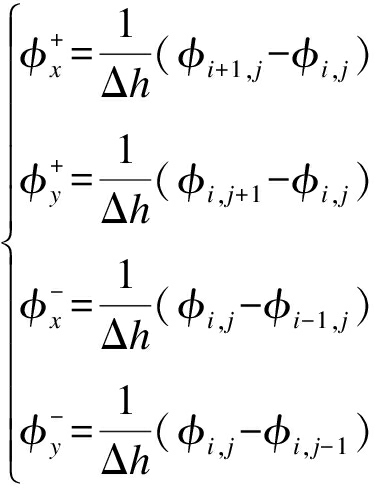
(11)
根据式(11)定义如下两个梯度，即
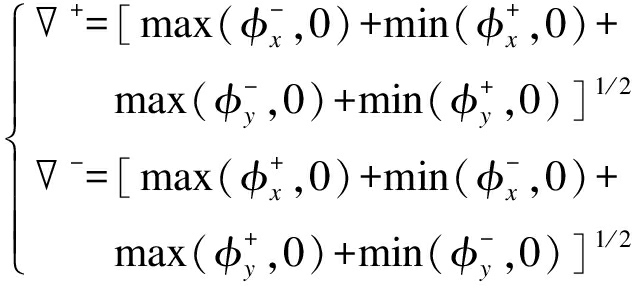
(12)
将式(11)、(12)代入式(10)可得
++min(vnij，0)-)=
(13)
通过式(13)的演化机制，水平集函数可以不断向前演化.由于数值计算中使用了有限差分法，因此需要注意时间步长Δt的选择，在给定空间网格间距Δh的条件下，需满足
HΔt≤Δh
(14)
设定目标点xf，当目标点处的φ(xf)值不大于零时，可以判断零水平集已经到达目标点，此时，可以得到路径规划所需时间为
在零水平集前向演化中，已经提出并保存了各个时刻的零水平集曲线，在Txf时刻，机器人应该处于目标点xf的下方，且因为离散的原因，此时的下方并不一定是正下方.目标点xf在Txf时刻对应零水平集曲线的投影为
从该点开始逆向计算路径，将式(10)离散化可得
=-Vf(x，t)-vn
(15)
在有向外力作用下机器人路径规划问题的仿真实验中，配置空间规约在二维平面上，空间的两个坐标轴x、y都在[-1，1]之间.为进行数值计算，x和y方向上被均分成m×n个网格，分别按i和j来索引.空间内的外力速度场Vf在这些网格上取值，其中第(i，j)个网格点上的外力速度为Vf(i，j).在以下的仿真实验中，机器人的速度保持恒定，在仿真中设定为vn=0.28 m/s.
为验证算法的基本功能以及数值方法的精度，本文对恒定外力场中机器人的路径进行规划，空间内存在恒定的外力速度场Vf=0.2 m/s，仿真结果如图2所示.由图2可知，算法的基本功能已经实现，并且数值算法的精度可以保证最优路径的生成.在外力影响下，机器人向左运动速度减慢，向右速度加快，在曲线上的表现为单位时间原点左侧的曲线被挤压，而右侧曲线被拉伸.
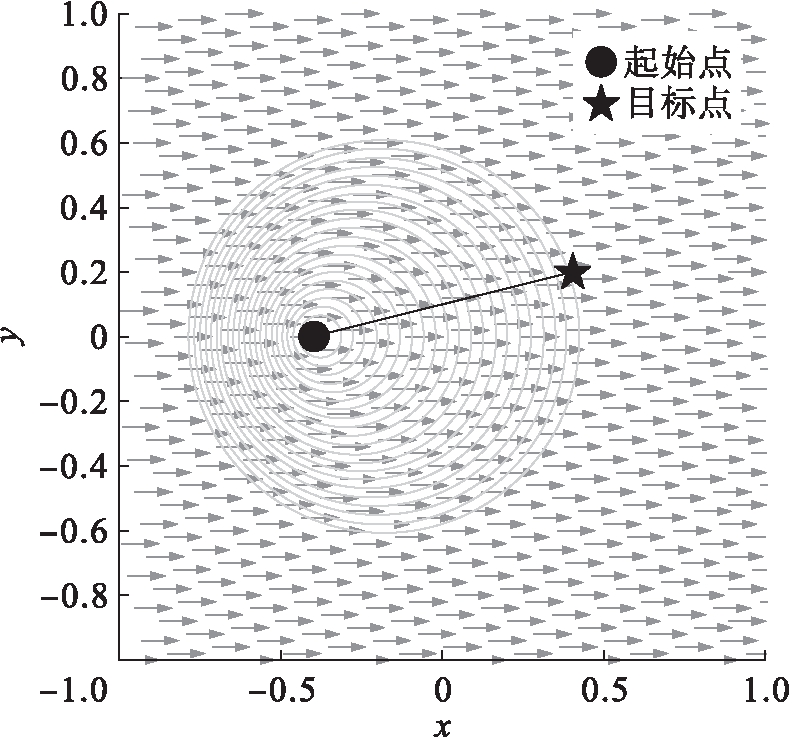
图2 在恒定外力场中机器人的路径规划
Fig.2 Path planning for robot in constantexternal force field
不同速度下机器人的路径规化如图3所示.图3中空间存在着带状速度场，同样结构的外力场中，通过调整速度场的大小进行了6组实验.仿真结果表明，路径规划算法可以有效利用外力来加快自己的运动，并且在强流场中算法仍能保持原有的精度.在较小的速度场中，穿过速度场的路径与x轴的夹角较大，表示机器人可以更容易地穿越速度场；在较大的速度场中，该角度变小，表示在较大的速度场中，机器人可以移动的范围变小，同时算法可以精准地确定进入速度场的位置，以确定在较强的外力作用下所规划出的路径仍然保持可行性.
弯曲封闭的外力场在自然界中也很常见，如大气和海洋中存在的涡旋.图4是模拟涡旋生成的一种弯曲外力场，模拟场为同心圆结构，距圆心越远，速度越大.圆心处速度最小，为0 m/s，边界处最大，为1 m/s.仿真选取了3组起始点和终点作为比较，同时以虚线给出了A*算法得到的路径结果.结果显示，在弯曲外力场下，路径可以有效利用外力场，并且生成的路径突破了传统的节点取点方式，形成了连续光滑的曲线路径.A*路径由于必须在网格点上取点，因此要牺牲一些距离来取网格点.从时间上来看，Level Set路径完成后，A*路径还没有到达终点，图4中以“×”表示与Level Set相同时间的A*所能到达的点.
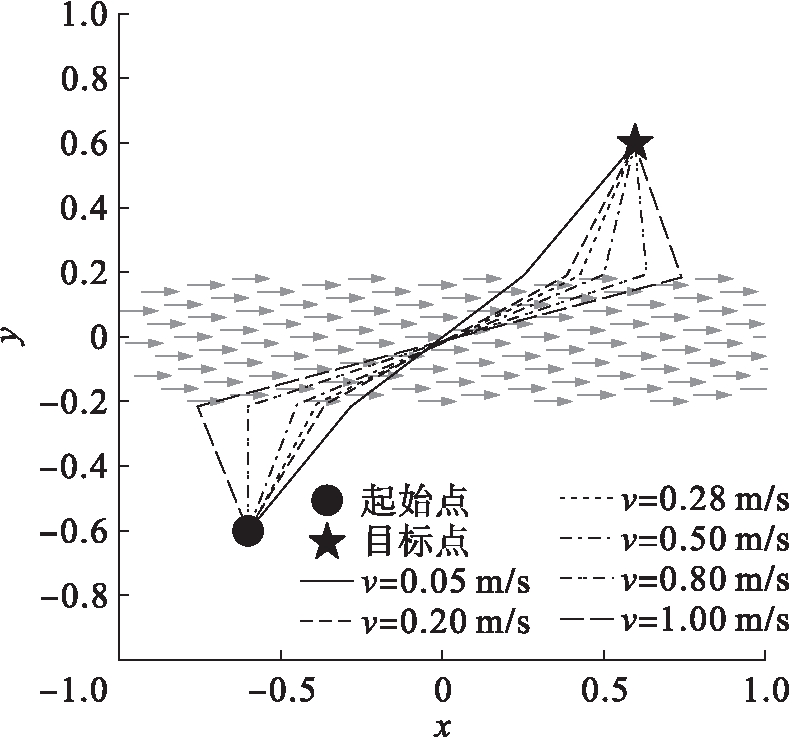
图3 在不同速度下机器人的路径规划
Fig.3 Path planning for robot under different velocity
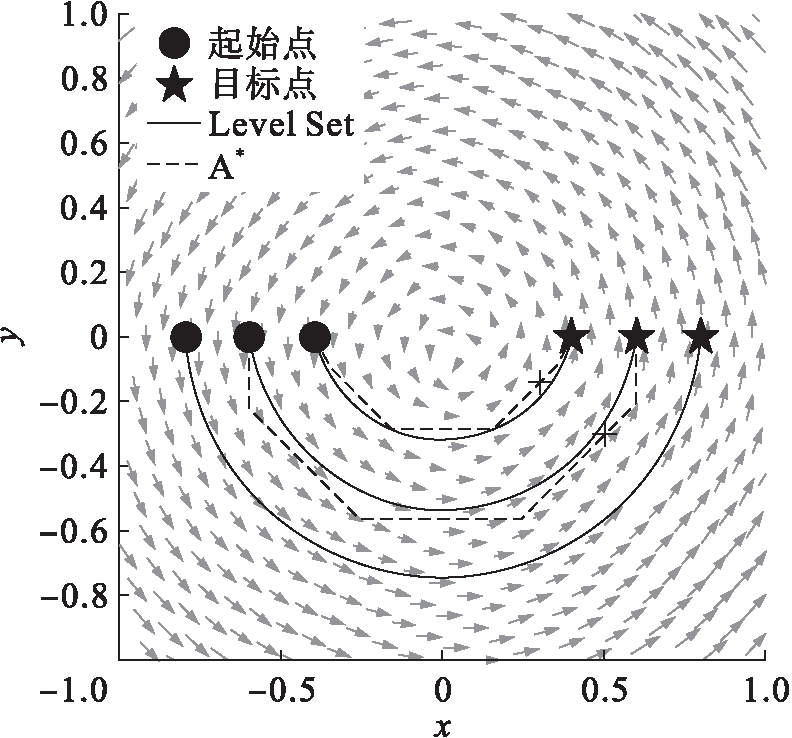
图4 在弯曲外力场中机器人的路径规划
Fig.4 Path planning for robot in bendingexternal force field
在最外层一组仿真中，A*没能找到合适的路径，分析原因可知，基于格点的搜索对于在外力场中机器人的可通行角度有限制，而基于数值方法的Level Set方法则可以避免这一限制.
本文研究了在有向外力场作用下机器人的路径规划问题，首先给出了路径规划的数学模型，基于Level Set方法推导出了连续路径规划的哈密尔顿雅克比方程，通过解该方程得到时间最优路径.通过改进了数值计算方法，提高了算法的数值精度，保证了规划路径的连续性，突破传统路径规划方法基于网格的搜索方式，同时保证了在强外力场中路径的可行性.
[1]孙炜，吕云峰，唐宏伟，等.基于一种改进A*算法的移动机器人路径规划 [J].湖南大学学报(自然科学版)，2017，44(4)：94-101.
(SUN Wei，LÜ Yun-feng，TANG Hong-wei，et al.Mobile robot path planning based on an improved A* algorithm [J].Journal of Hunan University (Natural Sciences)，2017，44(4)：94-101.)
[2]冯辉，刘梦佳，徐海祥.基于AHPSO算法的无人艇多目标路径规划 [J].华中科技大学学报(自然科学版)，2018，46(6)：59-64.
(FENG Hui，LIU Meng-jia，XU Hai-xiang.Multi-target path planning for unmanned surface vessel based on adaptive hybrid particle swarm optimization [J].Journal of Huazhong University of Science and Technology (Natural Science Edition)，2018，46(6)：59-64.)
[3]Garau B，Alvarez A，Oliver G.Path planning of autono-mous underwater vehicles in current fields with complex spatial variability：an A* approach [C]//2005 IEEE International Conference on Robotics and Automation.Barcelona，Spain，2005：194-198.
[4]刘琳，李春媛，陈彦虎，等.基于路由节点的最优油耗路径规划模型 [J].重庆大学学报，2018，41(7)：73-81.
(LIU Lin，LI Chun-yuan，CHEN Yan-hu，et al.Research on path planning model of optimal fuel consumption based on routing nodes [J].Journal of Chongqing University，2018，41(7)：73-81.)
[5]崔宝侠，王淼弛，段勇.基于可搜索24邻域的A*算法路径规划 [J].沈阳工业大学学报，2018，40(2)：180-184.
(CUI Bao-xia，WANG Miao-chi，DUAN Yong.Path planning for A* algorithm based on searching 24 neighborhoods [J].Journal of Shenyang University of Technology，2018，40(2)：180-184.)
[6]崔宝侠，宋佳瑞.未知环境下机器人避障及动态目标追踪 [J].沈阳工业大学学报，2018，40(3)：292-298.
(CUI Bao-xia，SONG Jia-rui.Obstacle avoidance and dynamic target tracking of robot in unknown environment [J].Journal of Shenyang University of Techno-logy，2018，40(3)：292-298.)
[7]Rhoads B，Mezic I，Poje A.Minimum time feedback control of autonomous underwater vehicles [C]//IEEE Conference on Decision and Control.Atlanta，USA，2010：5828-5834.
[8]Petres C，Pailhas Y，Patron P Y，et al.Path planning for autonomous underwater vehicles [J].IEEE Tran-saction of Robot，2007，23(2)：331-341.
[9]Lolla T，Lermusiaux P F J，Ueckermann M P，et al.Time-optimal path planning in dynamic flows using level set equations：theory and schemes [J].Ocean Dynamics，2014，64(10)：1373-1397.