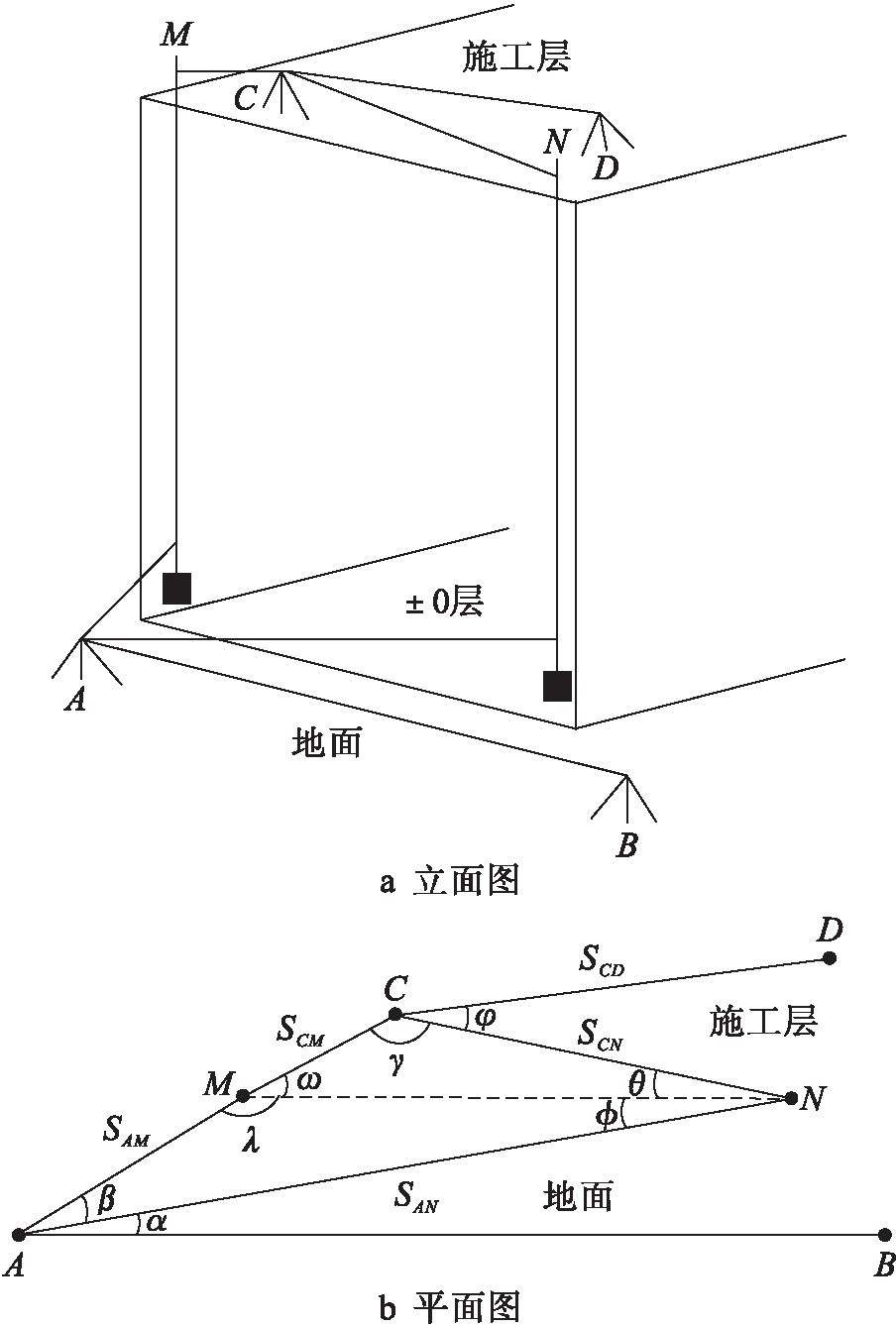
图1 联系三角形法竖向传递控制点
Fig.1 Vertical transmission of control pointsin connected-triangle method
控制点竖向传递是高层建筑物施工测量工作中最重要的一项内容,其精度直接决定了建筑物的垂直度和细部放样点位精度.当前高层建筑物的施工环境往往十分复杂,如场地狭小、工艺和设备复杂、各工种之间常相互干扰、周边建筑物高大且密集等,这些因素常导致传统的控制点竖向传递方法受环境条件的制约而不能使用,例如:外控法轴线传递仅适用于施工场地四周宽阔无障碍的情况[1],现代高层建筑往往采用封闭施工以减小对周围环境的影响,因此外控法往往不能应用;内控法需要在各层的楼板上预留洞[2],这往往造成控制点传递与施工之间相互干扰,有时碰到异形建筑物内部各楼层间柱梁交错使各层之间预留孔处垂直方向通视困难,都会导致该方法不能应用.当传递距离较远时激光铅垂仪的激光斑半径增大从而增大了传递误差,为了减小这种影响,文献[3-7]提出采用分段投测和分段控制的内控法,这虽然给控制点投测带来了便利,但同时也带来了误差累计,降低了精度;文献[8]提出采用GPS静态定位模式测量施工层控制点的方法,精度达到5 mm以内,但该方法往往受到塔吊、施工震动、施工遮挡等环境因素的限制.如果在建筑物外墙外侧设置两根重锤线,将地面和施工层控制点与重锤线联测,可实现控制点坐标的竖向传递.基于此本文提出了利用联系三角形法和无定向导线法将控制点和重锤线联测实现控制点竖向传递的方法,该方法不仅能克服以上提到的种种不利于环境因素的影响,而且精度可靠,操作灵活方便.
高层建筑物施工中,其外墙外侧十分便于悬挂吊锤线或利用铅垂仪投点,这就为借助铅垂线来传递控制点提供了便利.图1为联系三角形法竖向传递控制点示意图.图1中,A、B为地面控制点,C、D为在施工层上新建的控制点标志,M、N为设置在外墙外侧的两根吊重锤的钢丝.在A点安置全站仪,后视B,通过精密角度、距离测量可获得M、N的精确坐标和直线MN的方位角;在C点安置全站仪,对M、N、D进行精密角度、距离测量,可精确地确定C、D、M、N的相对位置关系,进而获得C、D的坐标和其连线的方位角.具体如下:
1) 外业工作.
① 在地面上A点安置仪器,B点安置目标,利用全圆方向法精确测量水平角α、β;精确测量水平距离SAM、SAN,如图1b所示.
② 在施工层上C点安置仪器,D点安置目标,利用全圆方向法精确测量水平角γ、φ;精确测量水平距离SCM、SCN、SCD.
2) 内业计算.
① 检核测角测距精度.由地面的观测数据计算两吊锤线的水平距离,即

图1 联系三角形法竖向传递控制点
Fig.1 Vertical transmission of control pointsin connected-triangle method
(1)
由施工层的观测数据计算两吊锤线的水平距离,即
(2)
计算差值ΔS=SMN1-SMN2,差值应不超过2 mm,取平均值作为SMN.
② 由地面观测数据计算角度.按正弦定理,![]() 计算角度φ、λ.
计算角度φ、λ.
③ 由施工层观测数据计算角度.按正弦定理,![]() 计算角度θ、ω.
计算角度θ、ω.
④ 将地面控制点、吊锤线、施工层控制点组成一条经过小角φ、θ的导线,即B-A-N-C-D,按照导线计算方法获得施工层CD边的坐标方位角和控制点C的坐标,其表达式为
αCD=αAB-α+φ+θ-φ±180°n
(3)
XC=XA+SANcosαAN+SCNcosαCN
(4)
YC=YA+SANsinαAN+SCNsinαCN
(5)
1.2.1 方位角精度分析
对式(3)按误差传播定律求导,CD边坐标方位角的中误差可表示为
(6)
mαAB决定于地面控制测量的精度,该建筑物在整个施工过程中都使用该组控制点,其误差对建筑物垂直度没有影响,完全可以忽略.α、φ的精度决定于地面、施工层上角度测量的精度;φ、θ是计算得到的,其精度不但受测角、量边误差的影响,还受三角形图形条件的影响,本文重点讨论mφ、mθ的情况.
对式![]() 按误差传播定律求导,可求得φ角中误差mφ的表达式为
按误差传播定律求导,可求得φ角中误差mφ的表达式为
(7)
进一步全微分求解并化简,可得
(8)
如果使地面、施工层的测量三角形呈伸展形状,即β、φ、θ、ω接近零度,此时tanφ≈0、cosφ≈1,式(8)可简化为
(9)
同理
(10)
由前文分析可以得出,当测量三角形呈伸展形状时,SAM≪SAN,所以mφ≪mλ,此时量距误差对角度误差影响非常小.同理在施工层上,SCM≪SCN,mθ≪mω.由此得出,欲提高控制点竖向传递的精度,除提高角度观测精度外,还要注意:
1) 使地面、施工层上的测量三角形呈伸展形状;
2) 尽量减小SAM和SCM的值;
3) 尽量增大两吊锤线M、N的间距(将两吊锤线分别布置于某一长外墙外侧面的两端);
4) 计算时应选经过小角φ、θ的导线.
1.2.2 坐标精度分析
对式(4)、(5)按误差传播定律求导,C点坐标的中误差可表示为
(11)
(12)
A点的误差mA非常小,且该建筑物整个施工过程中都使用该点传递坐标,所以其误差影响可以忽略.于是将式(11)、(12)合并化简可得
(13)
对于边AN、CN坐标方位角αAN、αCN的误差,按误差传播定律可推导得
mαAN=mα
(14)
(15)
由于铅垂线放样是在墙侧,可以选择外界条件影响小的时间段进行,当无法避免恶劣的外界条件时,可以利用激光铅垂仪投点.两吊锤线M、N的间距比较大,施工层控制点间的边长短,此时残余的投点误差对施工层控制点坐标的影响很小.
1.2.3 联系三角形法控制点竖向传递精度估算
本文按照较不利的情况对联系三角形法控制点竖向传递的精度进行估算.设测角中误差为5″,测距中误差为2 mm,SAM=4 m、SAN=24 m、SMN=20 m、SCM=4 m、SCN=16 m,则按本文方法计算有mφ=1″、mθ=1″、mαAN=5″、mαCN=5.2″、mαCD=7.2″、mC=2.9 mm.以此结果为基础,用极坐标法进行细部放样,放样过程中的测角中误差为5″,测距中误差为2 mm,放样距离S=20 m,则放样结果的总误差![]() 以二倍中误差为限差,即2mP=7.4 mm.根据《建筑工程质量检验评定标准》(GBJ301-88)规定,高层建筑物外墙面垂直度的限差为1/1 000且小于等于30 mm.从精度估算数据上看此方法是完全满足要求的.
以二倍中误差为限差,即2mP=7.4 mm.根据《建筑工程质量检验评定标准》(GBJ301-88)规定,高层建筑物外墙面垂直度的限差为1/1 000且小于等于30 mm.从精度估算数据上看此方法是完全满足要求的.
图2为无定向导线法竖向传递控制点示意图.图2中,A、B为地面控制点,M、N为吊锤线位置,C、D为施工层上的控制点.
1) 外业观测.
① 在地面上精密测量水平角α、β和水平距离SAM、SBN;
② 在施工层上精密测量水平角γ、φ和水平距离SCM、SDN、SCD.
2) 内业计算.
① 由地面观测数据计算两吊锤线M、N的坐标XM、YM、XN、YN,再按坐标计算两吊锤线间的水平距离SMN1;
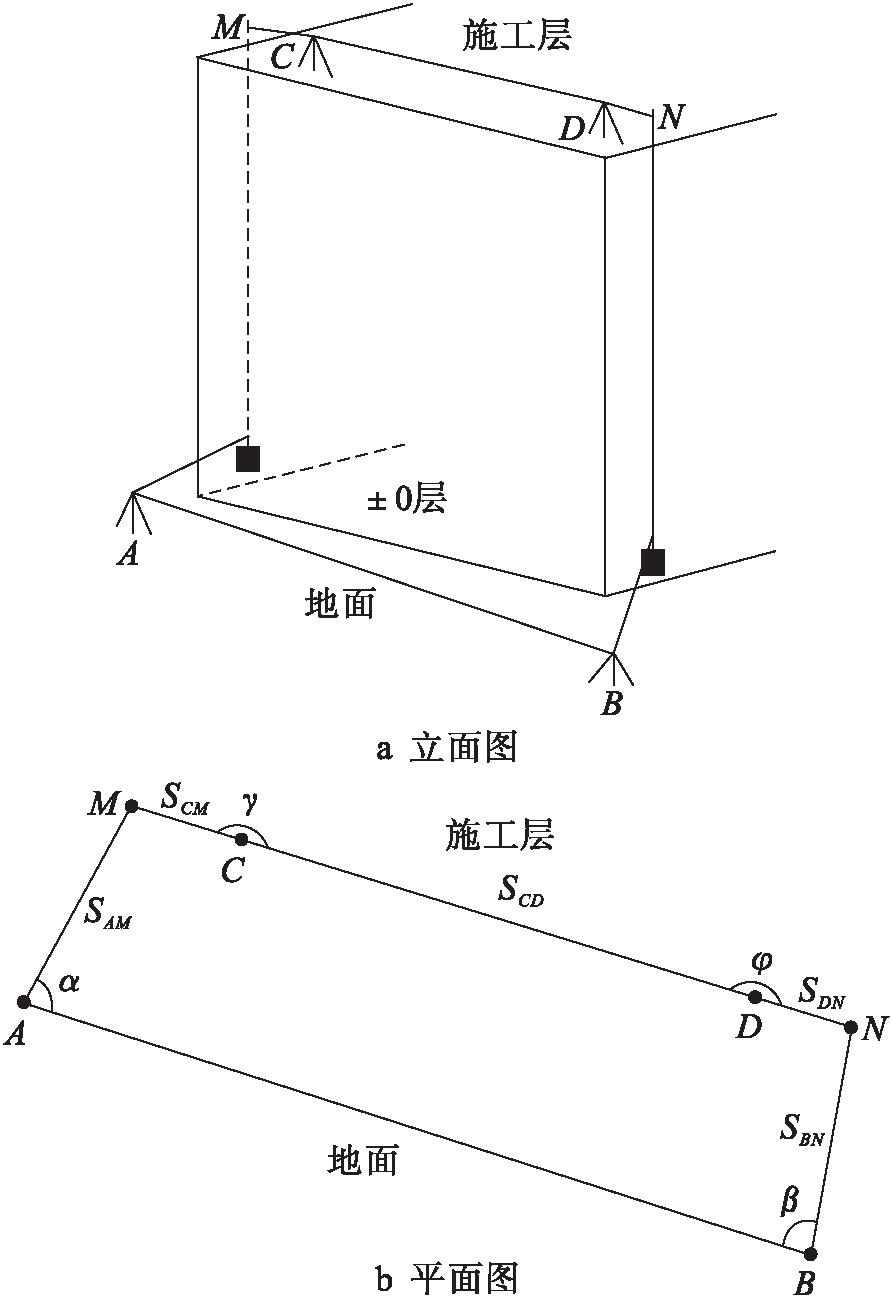
图2 无定向导线法竖向传递控制点
Fig.2 Vertical transmission of control pointsin non-oriented traverse method
② 由施工层观测数据计算两吊锤线M、N的水平距离SMN2,其过程为:假定M点坐标XM=0,YM=0,C点坐标XC=SCM,YC=0,再利用观测的数据γ、φ、SCD、SDN计算N点的假定坐标XN、YN,最后计算SMN2;
③ 计算差值ΔS=SMN1-SMN2,此数值应不超过2 mm;
④ 将吊锤线、施工层控制点组成一条无定向导线,即M-C-D-N,按照无定向导线计算方法获得C、D两点坐标.
无定向导线法传递控制点的误差来源于铅锤线投测误差、地面连接测量误差、施工层连接测量误差.由于两吊锤线间距较大,在投测时采取有效措施控制投点误差,因此,该误差对控制点传递的精度影响很小.
1) 地面连接测量误差的影响.
地面连接测量误差就是极坐标法测量两吊锤线坐标的误差,其表达式为
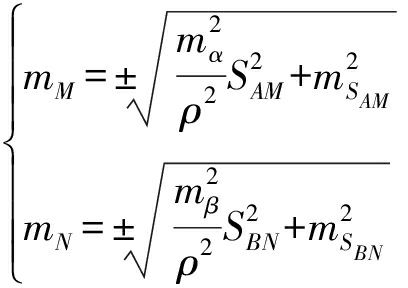
(16)
地面连接测量误差对坐标方位角传递误差的影响主要是由于两吊锤线坐标误差在垂直于两吊锤线连线方向上的分量引起的,其表达式为
(17)
由式(16)、(17)可以看出,将吊锤线M、N布置在靠近控制点处的墙体外侧,使其便于高精度量距,可以有效提高坐标和方位角传递的精度.
2) 施工层上连接测量误差的影响.
施工层上连接测量误差主要是由其测角误差miβ和量边误差mil所引起的,其对CD边坐标方位角的影响为
(18)
式中:mβ为测角中误差;RC-M、RC-N、RD-N分别为C-M、C-N、D-N的距离在MN连线上的投影长度;φ1、φ2、φ3分别为导线边CM、CD、DN与MN连线的夹角.
由式(18)可以看出,若将施工层上的无定向导线布置为直伸形(即M、C、D、N基本处于一条直线上),此时φi≈0,量边误差对导线边方位角的精度不产生影响.
综上所述,无定向导线法竖向传递控制点的方位角误差和坐标误差可表示为
(19)
(20)
3) 无定向导线法控制点竖向传递的精度估算.
按照较不利的情况对无定向导线法控制点竖向传递的精度进行估算.设测角中误差为5″,由于控制点与吊锤线距离近,便于精密量距,所以设测距中误差为1 mm.SAM=5 m,SBN=5 m,SMN=25 m,SCM=2.5 m,SDN=2.5 m,M、C、D、N四点位于一条直线上.则按本文方法计算有:mM=mN=1 mm,mαMN=11.8″,m上=4.5″,mαCD=12.6″,mC=1.4 mm.以此结果为基础,用极坐标法进行放样,放样过程中的测角中误差为5″,测距中误差为2 mm,放样距离S=20 m,则放样结果的总误差为![]() 以二倍中误差为限差,即2mP=6.0 mm.
以二倍中误差为限差,即2mP=6.0 mm.
从精度估算的结果可以看出,对方位角传递的精度进行测量时,联系三角形法的精度较高.主要原因是联系三角形法在构成最有利的图形条件后,量边误差对方位角精度几乎不产生影响.但是在范围很小的施工层上进行放样,两种方法的方位角传递误差对放样点位误差的影响几乎相当.
对坐标传递的精度而言,无定向导线法的精度较高.主要原因在于无定向导线的地面控制点距离吊锤线较近,便于精密量距工作的实施,而联系三角形法在构成最有利三角形后,设站点距离某一根吊锤线较远,难以实施精密量距.但是在进行了合理的精度保证措施后,两种方法的坐标传递误差相差很小.
总的来说,由于高层建筑物施工层的范围较小,一般不超过几十米,使用这两种方法传递的控制点进行放样结果的精度是相当的.
从观测图形和观测条件上进行比较.方法1需要将地面控制点、两根吊锤线、施工层控制点构成最有利的延伸形三角形,而且控制点与吊锤线间要便于精密测角量距.地面和施工层的联系三角形中各自有一条量距边长度较大,不便于精密钢尺量距,必要时需利用电磁波测距代替钢尺量距.方法2中,为了保证地面连接测量中两吊锤线坐标测量的精度,要求两控制点均应位于建筑物附近,以便于实施精密量距.由于两控制点均参与坐标和方位角的传递,所以应严格控制两控制点间的相对精度.由于地面和施工层的控制点与吊锤线间的距离都较短,为了保证距离测量精度,应采用精密钢尺测距的方法.
使用本文方法时,当遇到不利的环境,可以采用铅垂仪代替吊锤线进行投点.当建筑物外墙外侧不便于投点时,还可以将投点位置选在楼梯或电梯处.由地面直接向施工层投测,不会产生累积误差.
某一建设中的高层大楼位于唐山市中心区,大楼地上28层,建筑高度约为112 m,地下2层,外轮廓为边长约63 m的矩形.该大楼为钢骨和钢筋混凝土组合结构,由钢骨柱、钢梁等组成受力体系,结构复杂.大楼为集酒店、智能化办公、商业服务于一体的新型建筑,四周是高层住宅小区,施工场地狭小.工程对施工精度要求很高,这就对控制点竖向传递的精度提出了更高的要求,然而由于复杂的环境,导致外控法、GPS法竖向传递控制点均不能使用,而利用内控法传递控制点的过程中又受到了施工干扰,降低了精度和可靠性,所以在第25层以上都采用了本文提出的方法.图3为第25层控制点竖向传递示意图.其中,A、B为地面控制点,C、D为25层上的控制点,M1、N1为联系三角形法传递控制点时吊锤线的位置,M2、N2为无定向导线法传递控制点时吊锤线的位置.

图3 控制点竖向传递点位布设
Fig.3 Point layout for vertical transmissionof control points
投点工作选择在外界条件良好的时间,利用0.5 mm钢丝和60 kg重锤投点,投点误差非常小.角度测量采用两台2″精度的全站仪,在地面和楼顶每角观测4个测回.边长测量采用两把经鉴定的钢尺,每边串尺丈量4次,4次边长值互差要求小于2 mm,加各项改正数后取平均值.表1为控制点A、B的已知坐标.表2为利用联系三角形法的观测数据,其观测图形如图1所示.表3为利用无定向导线法的观测数据,其观测图形如图2所示.按照本文提出的方法进行了精度估算,结果如表4所示.对表2、3的数据进行计算,结果如表5所示.
结果表明,本文提出的控制点竖向传递的方法正确,精度满足要求,精度估算的结果与实际情况一致.
本文提出了借助吊锤线在建筑物外墙外侧投点,利用联系三角形法和无定向导线法进行控制点竖向传递的方法.该方法解决了在当前高大建筑物复杂的施工环境下,外控法、内控法和GPS法等传统方法由于受到场地、通视、施工干扰等影响而不能进行控制点竖向传递的问题.理论分析和工程应用结果表明,该方法具有精度可靠、操作方便、与施工之间的相互干扰小的优点.
表1 控制点竖向传递的起算数据
Tab.1 Initial data for vertical transmission of control points

XA/mYA/mXB/mYB/m起始方位角αAB6305.27585151.03006304.82625225.730590°20′42″
表2 联系三角形法竖向传递控制点的观测数据
Tab.2 Measured data of vertical transmission of control points in connected-triangle method

αβSAM/mSAN/mφγSCM/mSCN/mSCD/m1°06′16.5″6°08′38.2″7.47867.7331°47′20.5″145°59′20.2″2.93357.84756.251
表3 无定向导线法竖向传递控制点的观测数据
Tab.3 Measured data of vertical transmission of control points in non-oriented traverse method

αSAM/mβSBN/mγSCM/mφSDN/mSCD/m23°15′35.5″6.350229°53′35.2″6.2510179°46′20.5″4.0505180°13′40.2″3.150556.251
表4 两种控制点竖向传递方法的精度估算
Tab.4 Precision estimation of two vertical transmissionmethods of control points

方法坐标传递误差/mm方位角传递误差联系三角形法3.35.7″无定向导线法1.45.9″
表5 两种控制点竖向传递方法的计算结果比较
Tab.5 Comparison in calculated results of two verticaltransmission methods of control points
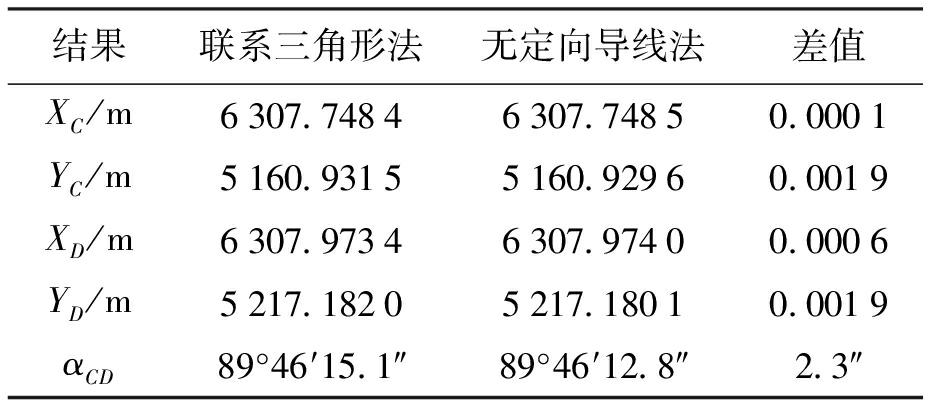
结果联系三角形法无定向导线法差值XC/m6307.74846307.74850.0001YC/m5160.93155160.92960.0019XD/m6307.97346307.97400.0006YD/m5217.18205217.18010.0019αCD89°46′15.1″89°46′12.8″2.3″
[1]兰泽英,刘洋.超高层建筑施工监测内容及技术体系研究 [J].测绘工程,2016,25(7):40-45.
(LAN Ze-ying,LIU Yang.Research on the content and technology system of super-high-rise building construction monitoring [J].Engineering of Surveying and Mapping,2016,25(7):40-45.)
[2]段鹏,彭浩.超高层建筑核心筒及电梯井偏差监测方法 [J].测绘通报,2016(3):83-86.
(DUAN Peng,PENG Hao.A deviation monitoring method for core tube and elevator shaft of ultra high-rise building [J].Bulletin of Surveying and Mapping,2016(3):83-86.)
[3]张具林,叶玉芹,谈虎,等.超高层建筑施工测量控制系统的建立与实施 [J].施工技术,2013,42(5):107-110.
(ZHANG Ju-lin,YE Yu-qin,TAN Hu,et al.Estab-lishment and implementation of construction survey control system for super tall buildings [J].Construction Technology,2013,42(5):107-110.)
[4]曾坤,李建成.超高层建筑测量关键技术研究 [J].测绘地理信息,2012,37(6):37-39.
(ZENG Kun,LI Jian-cheng.Key super technology of high-rise building surveying [J].Journal of Geoma-tics,2012,37(6):37-39.)
[5]陈秋计.一种已知点不通视条件下的施工放样新方法 [J].测绘通报,2016(9):81-83.
(CHEN Qiu-ji.A new method for construction layout on the difficult visibility condition between known points [J].Bulletin of Surveying and Mapping,2016(9):81-83.)
[6]甘明生,章平,李庆达,等.超高层建筑核心筒无平台轴线竖向投测技术 [J].施工技术,2016,45(18):77-80.
(GAN Ming-sheng,ZHANG Ping,LI Qing-da,et al.Vertical measurement technology of the core tube of super high-rise building without measurement platform [J].Construction Technology,2016,45(18):77-80.)
[7]哈乐,房立金.BP网络算法在平面运动测量误差补偿中的应用 [J].沈阳工业大学学报,2016,38(1):86-89.
(HA Le,FANG Li-jin.Application of BP network algorithm in error compensation of planar motion mea-surement [J].Journal of Shenyang University of Technology,2016,38(1):86-89.)
[8]王天应.GPS技术在超高层建筑施工监测中的应用 [J].地理空间信息,2012,10(4):55-58.
(WANG Tian-ying.Application of GPS in construction monitor of skyscraper [J].Geospatial Information,2012,10(4):55-58.)