随着列车的飞跃式提速,齿轮箱作为传动装置的重要部件,对其性能要求越来越严格.在列车高速行驶过程中,齿轮传动系统的工作环境极其恶劣,箱体内部存在复杂变化的油气两相流[1],从而对齿轮箱的润滑、密封等性能造成很大的影响.润滑油具有良好的润滑性、密封性、抗磨性及抗腐蚀性能,因而可以减轻齿轮箱内运动零件接触表面的磨损并降低产热量,进而起到清洗和冷却的作用,从而保证齿轮箱的正常工作[2-3].因此,研究齿轮箱的流场变化规律并选择合适的浸油深度对保证齿轮箱的正常高效运行非常重要.
目前关于齿轮箱流场的分析尚未得到系统研究.吴特[4]建立了齿轮箱二维仿真模型,应用动网格技术分析了齿轮箱内部流场的变化规律;刘志强、任崇会等[5-6]建立了齿轮箱三维流体模型,应用动网格技术研究了齿轮箱内的瞬时流场变化规律,相关试验结果表明,二维与三维仿真模型的流场变化具有一致规律,结构尺寸较小的模型可实现三维仿真计算,但结构尺寸较大的模型很难实现三维模拟.Li等[7]对齿轮进行了简化,忽略了齿形对齿轮搅动过程的影响.本文以时速380 km的动车组用齿轮箱为研究对象,且电机最大转速为5 900 r/min.由于齿轮箱的结构尺寸较大,建立三维仿真模型的计算规模十分庞大,现有计算机硬件难以满足仿真需求,因此,采用二维模型进行相关计算.目前齿轮转动过程主要采用动网格技术进行模拟计算.本文选用一种新方法,即采用Fluent软件中的MRF模型模拟齿轮转动,并结合VOF多相流模型对不同转速及不同浸油深度条件下的齿轮箱内油气两相流进行计算分析,并为齿轮箱的设计和安全可靠运行提供现实指导.
1 模型选取及建立
1.1 数学模型
1.1.1 湍流模型
当列车高速运行时,齿轮箱高速运转搅起润滑油并引起空气的剧烈运动,油气混合物在齿轮箱内部剧烈混乱地流动,使得箱体内部润滑油及空气运动变化复杂,因此,齿轮箱内部流体的流动应按湍流处理.
湍流模型中的RNG k-ε模型考虑了平流问题中的复杂旋流以及旋转流动,对ε方程进行了改进,有效地改善了计算精度,能够处理齿轮箱内部流线弯度较大及应变率较高的问题.因此,选择RNG k-ε方程湍流模型进行内部流体数值模拟[8],其控制方程如下:
(1)
(2)
式中:ρ为密度;k为湍动能;ui为湍流速度;ε为湍流耗散率;μeff为RNG k-ε模型对湍流粘度的修正值;Gk为平均速度梯度引起的湍动能产生项数值;![]() 为RNG k-ε湍流模型经验常数C1ε的修正系数;t为时间;xi、xj分别为不同方向的位移;C1ε、C2ε分别为RNG k-ε湍流模型中k方程和ε方程的模型常数,具体数值为C1ε=1.42,C2ε=1.68;αk、αε分别为湍动能和耗散率对应的紊流普朗特数,且具体数值分别常采用1.0和1.3.
为RNG k-ε湍流模型经验常数C1ε的修正系数;t为时间;xi、xj分别为不同方向的位移;C1ε、C2ε分别为RNG k-ε湍流模型中k方程和ε方程的模型常数,具体数值为C1ε=1.42,C2ε=1.68;αk、αε分别为湍动能和耗散率对应的紊流普朗特数,且具体数值分别常采用1.0和1.3.
1.1.2 多相流模型
对于齿轮箱内部润滑油和空气形成的复杂两相流问题,选用VOF多相流模型对齿轮箱内部流体流动特性进行仿真计算.
VOF模型的连续性方程、体积分数方程和动量方程分别为
![]() +
+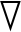 (ρv)=0
(ρv)=0
(3)
![]() +v
+v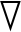 al=0
al=0
(4)
![]() +
+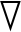 (ρvv)=-
(ρvv)=-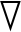 p+
p+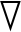 [μ(
[μ(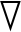 v+
v+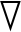 vT)]+
vT)]+
ρg+F
(5)
式中: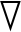 为哈密尔顿算子;v为速度矢量;μ为流体动力粘度;g为重力加速度;p为压强;F为表面张力的等价体积力形式;al为第l相的体积分数.
为哈密尔顿算子;v为速度矢量;μ为流体动力粘度;g为重力加速度;p为压强;F为表面张力的等价体积力形式;al为第l相的体积分数.
设al下标l=1和2分别代表空气和油液,则
a1+a2=1
(6)
气液两相流中由于表面张力及壁面粘附引起的动量方程源项表达式为
![]()
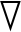 al/(ρl+ρm)
al/(ρl+ρm)
(7)
式中:σ为表面应力张量;k′为气液两相界面曲率,下标l、m代表不同相.
1.1.3 动参考坐标系模型
MRF模型的整个模拟计算区域被划分成多个较小的子域,每个子域可以拥有各自的运动方式,如静止、旋转运动和平移运动.在每个子域内分别进行控制方程计算,在相邻子域的相互交界面上通过边界设置实现各个子域流场的信息互换.
对于一对啮合的齿轮而言,在啮合位置建立两个齿轮的旋转域会在空间上发生干涉,这样就需要将一对啮合齿轮拉开,并通过设置圆柱体将两个啮合齿轮分别进行包裹,从而保证圆柱体与圆柱体之间以及圆柱体与被包裹的齿轮之间保留适当的距离.定义齿轮和圆柱体之间的包裹空间为旋转域,因而齿轮箱内部流体区域共有两个旋转域.通过定义旋转域的转速实现齿轮的旋转,并通过定义两组边界来实现静止域和旋转域的信息交换.
1.2 几何模型
利用UG参数化建模方式建立啮合齿轮的实体模型,主、从动齿轮选用斜齿轮,斜齿轮具有啮合性能好、传动平稳等优点.传动齿轮基本参数如表1所示,齿轮箱流体域模型如图1所示.
表1 传动齿轮基本参数
Tab.1 Basic parameters for transmission gear

齿轮法向模数压力角/(°)螺旋角/(°)中心距/mm齿数分度圆直径/mm主动轮6201838035220.81从动轮6201838085536.25
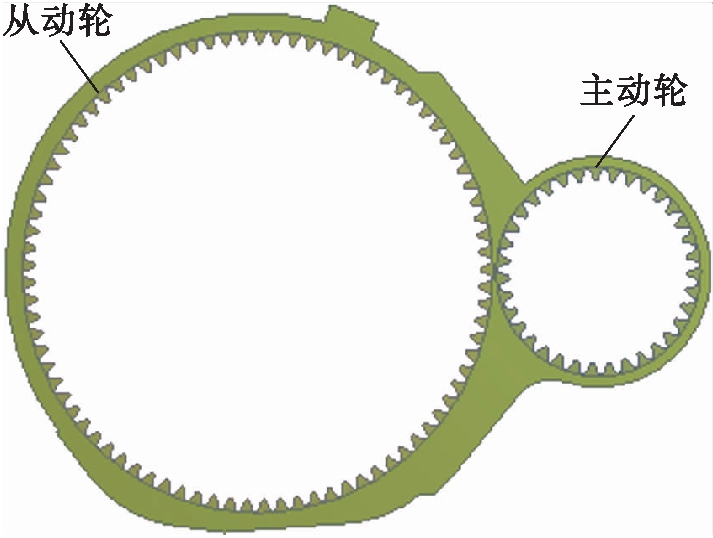
图1 齿轮箱流体域模型
Fig.1 Fluid domain model for gearbox
初始网格质量对仿真结果至关重要,将建立的齿轮箱内部流体模型导入Fluent软件中进行网格划分和边界设置,内部流体域采用三角形网格进行离散.齿轮啮合处附近局部网格如图2所示,且初始网格共有39 242个节点、67 784个单元.

图2 局部网格
Fig.2 Local grid
1.3 边界条件及求解方法
齿轮箱内含有由润滑油和空气构成的复杂两相流,多相流模型选用VOF模型,第一相设定为空气,第二相设定为润滑油.本文选用Basf-Emgard RW-A 75W-90润滑油,65 ℃时润滑油粘度为0.036 9 Pa·s,密度为837 kg/m3.
应用MRF模型对不同工况下的箱体内部流场进行动态实时仿真,选用RNG k-ε湍流模型与基于压力的分离求解器,并采用标准壁面函数处理近壁面区域的流动问题.齿轮箱壁面设置为无滑移模式,采用PISO算法进行压力![]() 速度耦合.当连续性方程、速度方程、湍动能、湍动能耗散率与油液体积分数方程的残差均小于1×10-5时,即可认为计算收敛.
速度耦合.当连续性方程、速度方程、湍动能、湍动能耗散率与油液体积分数方程的残差均小于1×10-5时,即可认为计算收敛.
2 齿轮箱动态模拟结果
2.1 齿轮箱内部流体分布
齿轮箱的润滑油深度对齿轮传动系统温度场及整体性能具有很大影响[9].如果润滑油深度太小,会导致齿轮润滑及箱体散热不足;如果润滑油深度过大,会增大搅油损失,将对齿轮传动系统的润滑和密封性能造成不良影响.
为了选择合适的润滑油深度,计算了齿轮箱不同润滑油深度对流场的影响.设定齿轮以额定功率运行,小齿轮顺时针旋转,转速为5 900 r/min,取齿轮箱内大齿轮润滑油深度分别为1~4倍齿高.
当齿轮箱运动达到动态平衡时,润滑油分布趋于稳定,不同浸油深度条件下齿轮箱内的润滑油分布如图3所示.图3中蓝色代表空气,红色代表润滑油,其他不同颜色代表润滑油的不同体积分数.由图3a、b可见,当润滑油深度为1、2倍齿高时,随着啮合齿轮的高速旋转,在离心力的作用下箱体底部的润滑油在齿轮箱内发生飞溅,润滑油小油团沿箱体内壁聚集,而齿轮箱内部空间的油滴较少.由图3c可见,当润滑油深度为3倍齿高时,箱体内壁存在较多的润滑油小油团,齿轮箱内部空间具有较多的小油滴与弥散油雾,从而可对箱体起到冷却降温效果,而且在大、小齿轮的啮合区域存在较多微小油滴,这对齿轮工作表面起到了冲洗和润滑作用,使得齿面不发生直接接触,保证了齿轮的有效使用.由图3d可见,当浸油深度为4倍齿高时,箱体内的润滑油虽然被充分搅起,但箱体底部存有大量润滑油,增加了搅油损失.由此可见,当为齿轮箱注油时,选择浸油深度为3倍齿高时可以充分发挥润滑油的作用.
2.2 齿轮箱内部流体速度场
列车运行速度是影响齿轮箱密封及泄露性能的重要因素[10],因而对不同转速条件下的速度场进行了分析.设定大齿轮浸油深度为3倍齿高,且小齿轮顺时针旋转.图4为稳态时小齿轮在最大运行速度5 900 r/min条件下某一时刻的速度分布.由图4可知,齿轮边界处流体流速较高,越靠近箱体内壁流速越小.齿轮啮合区流体速度最大,且速度最大值达到了92.4 m/s,这主要是因为在大、小齿轮的啮合区域,油气两相持续受到前后两对轮齿的挤压和分离作用,在极短时间内斜齿轮螺旋角的存在使得轮齿啮合线先由短变长,再由长变短并形成了狭小流体空间,且油气两相在此狭小空间中不断发生剧烈变化.
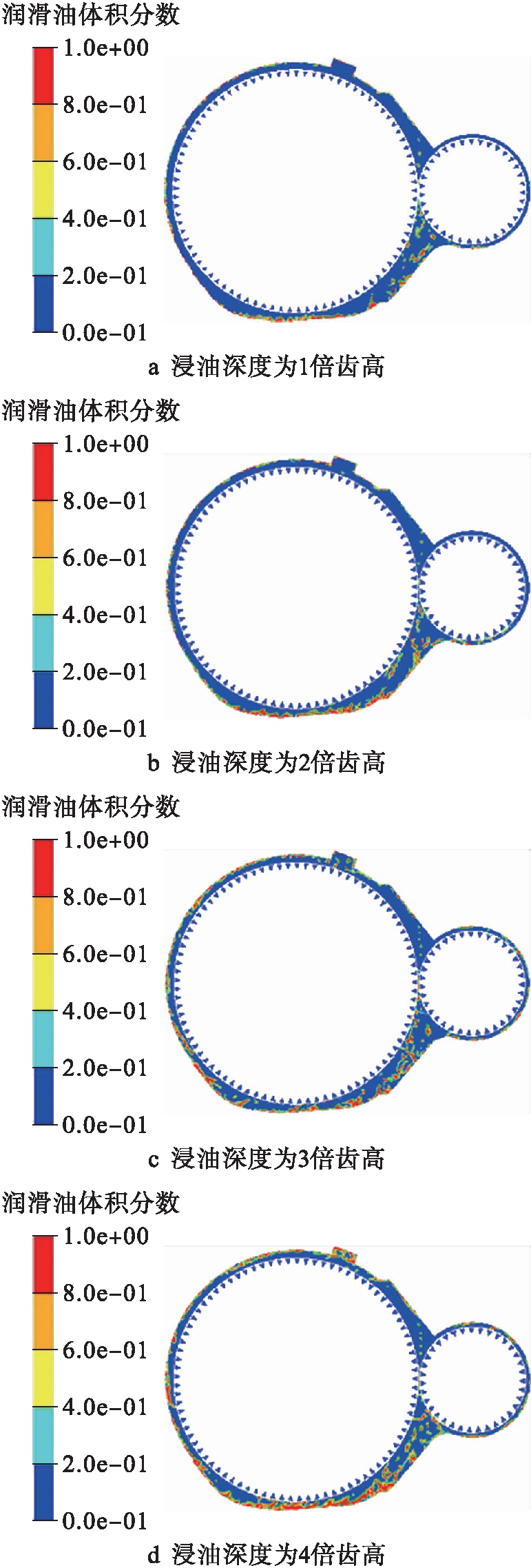
图3 不同浸油深度下润滑油分布
Fig.3 Lubricating oil distribution under different oil immersion depths
为了研究不同转速下箱体内部流体的瞬时速度变化,设定主动轮转速分别为2 000、4 000、5 900 r/min,内部流体速度最大值随时间的变化曲线如图5所示.由图5可见,在齿轮开始运转一段时间内,速度呈上升趋势,最后分别稳定在一定范围内波动:当主动轮转速为2 000 r/min时,内部流体速度最大值稳定在40~48 m/s范围内;当主动轮转速为4 000 r/min时,速度最大值稳定在65~70 m/s范围内;当主动轮转速为5 900 r/min时,速度最大值稳定在90~96 m/s范围内.
图4 5 900 r/min下速度分布
Fig.4 Velocity distribution at 5 900 r/min
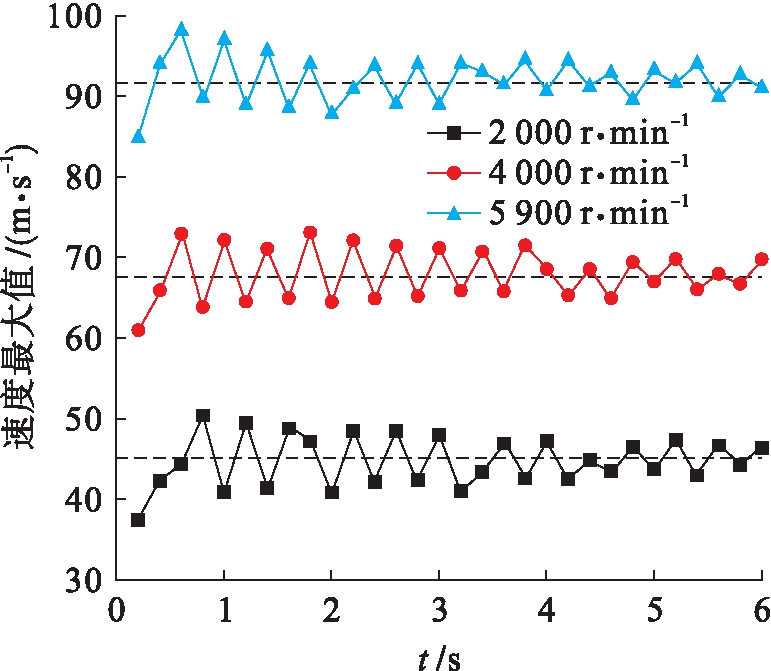
图5 不同转速条件下速度最大值变化曲线
Fig.5 Change curves for maximum speed at different rotational speed
选取图5中不同转速条件下内部流体速度最大值的平均值,得到箱体内部流体的最大速度平均值随转速的变化曲线,结果如图6所示.由图6可见,随着齿轮转速的增大,流体的最大速度平均值随之增大并呈线性增长.
2.3 齿轮箱内部流体压力场
在齿轮的啮入和啮出区域,流体分布和受力状态均不相同,导致二者之间出现了压力差,在长时间作用后齿轮产生形变,造成轮齿间的润滑间隙减小甚至消失,导致两轮齿直接接触,甚至引起齿轮传动失效,从而直接影响了齿轮寿命.
设定润滑油深度为3倍齿高,主动轮转速为5 900 r/min.图7为内部流体运动达到动态平衡时某时刻的压力分布,且啮合处下方为齿轮啮合入口,上方为齿轮啮合出口.由图7可知,随着齿轮的旋转,轮齿将要进入啮合区时的压力值最大,并形成了局部高压,且最高压力值达到42 kPa.当齿轮啮合后,轮齿将要脱离啮合区时压力值最小,并形成了局部低压,最低压力值达到-31 kPa.出现这种现象主要是因为当齿轮高速旋转时,在齿轮进入啮合的过程中,将要进入啮合区的油气混合物瞬间聚集在啮合区域前,导致压力急剧升高,当达到正压峰值后,油液速度迅速增大,并在压力作用下进入啮合区,因而啮合部位的高压会以液压方式传递出去,从而保护了齿轮.在两个啮合齿轮脱离啮合的过程中,润滑油得不到及时填补,随后很快形成了一个真空区域,当达到负压峰值后又恢复正压.不同转速条件下箱体内部的压力分布规律基本一致且差别较小,这里不再赘述.
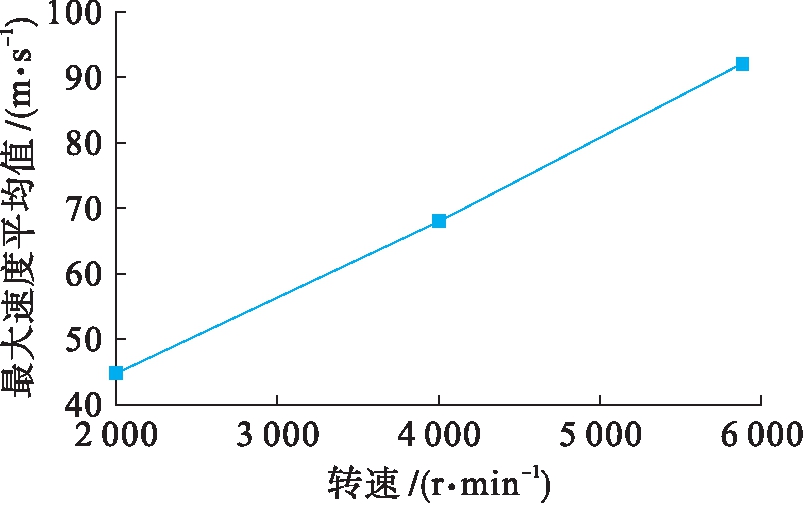
图6 最大速度平均值与转速的关系
Fig.6 Relationship between average value of maximum speed and rotational speed
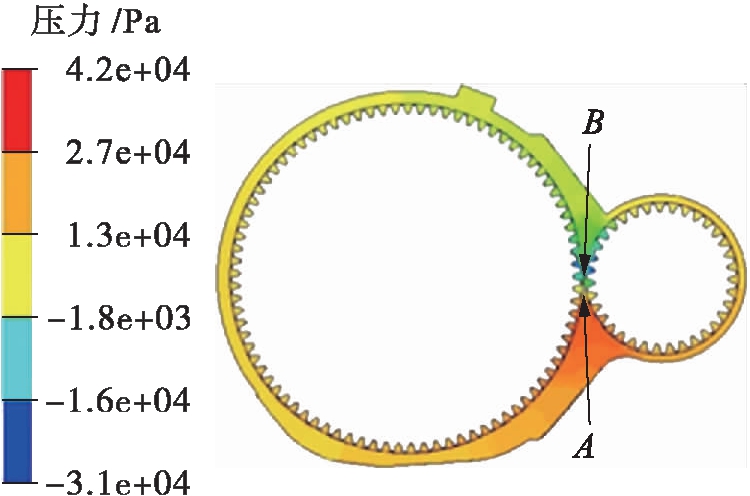
图7 流体压力分布
Fig.7 Fluid pressure distribution
为了研究齿轮啮入和啮出区域的压力瞬态变化过程,选取图7中A、B两点作为分析压力随时间变化的参考点.由图7可见,A点为齿轮啮入区域参考点,B点为齿轮啮出区域参考点.设定参考压力为一个大气压,高于一个大气压时的压力为正值,低于一个大气压时的压力为负值.
图8为不同转速条件下两参考点的压力值瞬态变化曲线.随着齿轮运行时间的推移,压力值发生波动,但压力分布规律基本不变,因此,选择0~0.6 s为研究时间范围.在齿轮启动初始时刻,两参考点的压力值未发生变化,这是因为从齿轮开始转动到齿轮带起润滑油接触参考点并引起参考点的压力变化需要一定时间,压力变化表现出启动瞬态行为,即啮入区和啮出区压力值相同,并在压力为零附近浮动,此时压力大小为外界大气压.随着时间的推移,转速越大,压力开始变化的时间点越早,这是因为转速越大,润滑油进入齿轮啮合区的速度越快,最终啮入点A的压力表现为正压,啮出点B的压力表现为负压,并最终稳定在一定范围内波动.
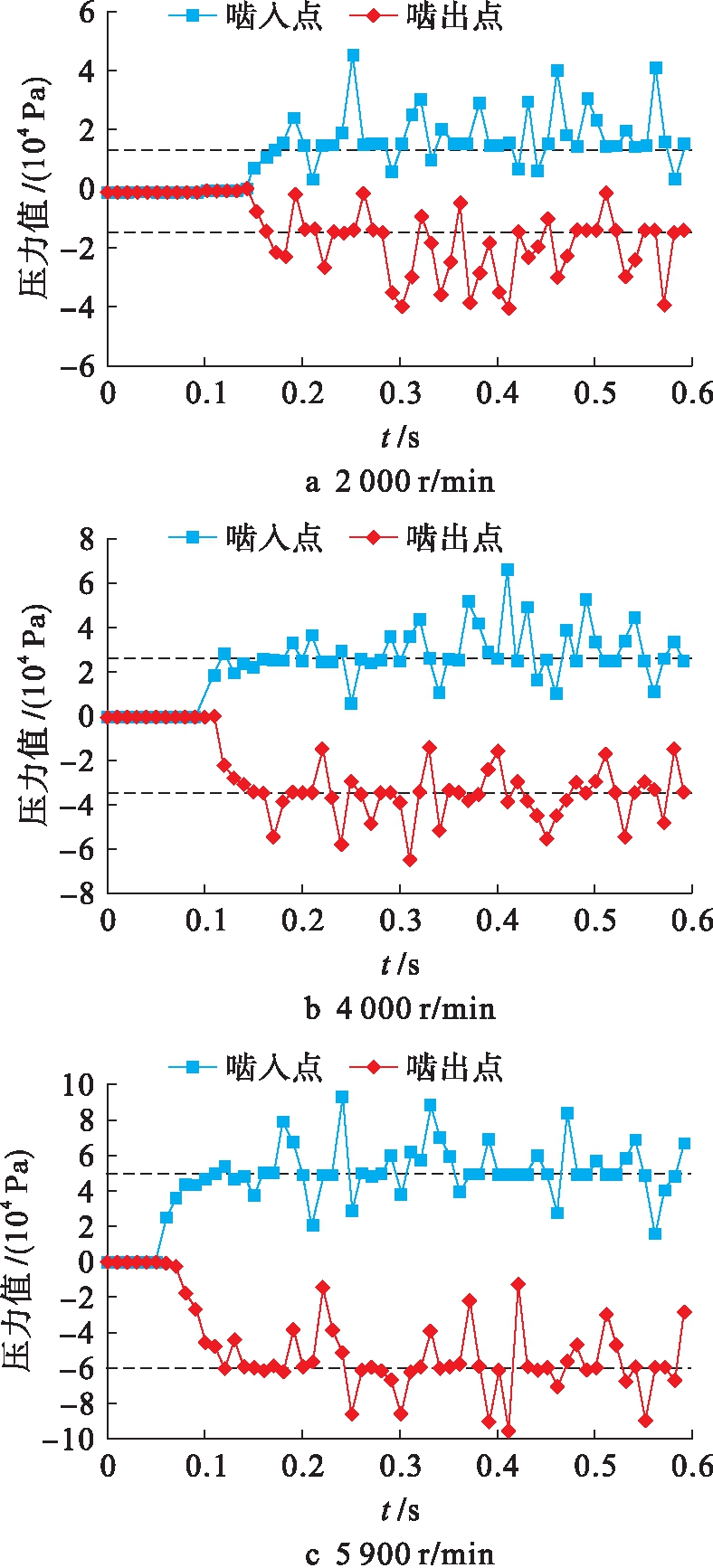
图8 不同转速下压力值瞬态变化曲线
Fig.8 Transient change curves of pressure at different rotational speed
为了更精确地研究转速对箱体内部压力场的影响,在齿轮箱运行达到动态平衡后,选取不同主动轮转速条件下不同时刻齿轮箱内部啮入点A和啮出点B的压力平均值作图,结果如图9所示.
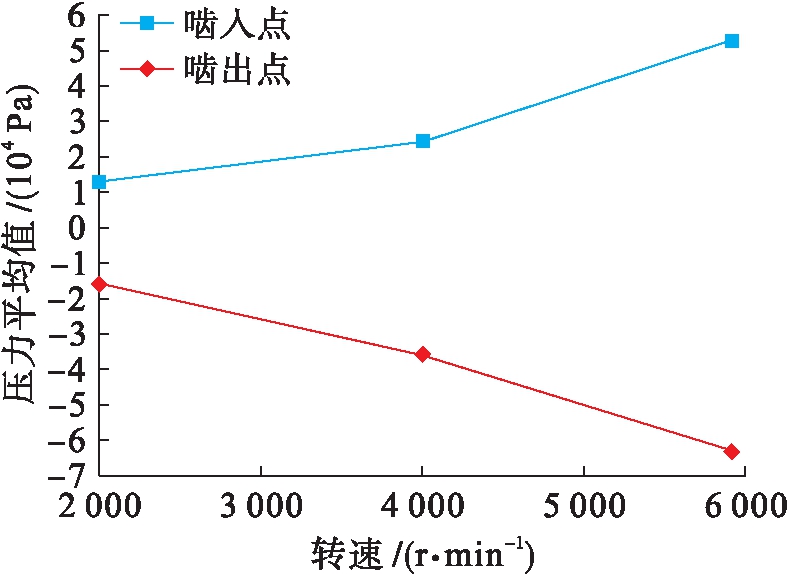
图9 压力平均值和转速的关系
Fig.9 Relationship between average pressure and rotational speed
由图9可知,当润滑油深度一定时,随着转速的提高,箱体内部流体压力最大值和最小值的绝对值呈非线性增大,且增速逐渐增大,表明转速对压力的影响也逐渐增大,这与文献[5]的试验结果一致.图9中压力最大值与最小值曲线之间围成的部分为压力差.由图9可知,齿轮转速越大,压力差越大,相应地齿轮受到箱体内部流体的作用力越大,齿轮越容易变形,从而使得齿轮寿命越短.
3 结 论
针对自主化研究的齿轮箱传动装置,采用多旋转坐标系方法模拟了高速齿轮箱流场分布情况,并得出以下结论:
1) 通过对比不同浸油深度下的润滑油分布,确定3倍齿高的浸油深度既可以充分发挥润滑油的作用,又不会由于浸油深度过大而增大产热量.
2) 当转速为5 900 r/min时,齿轮啮合区流体速度最大值达到92.4 m/s;不同转速下压力变化规律相同,并最终稳定在一定范围内波动.
3) 齿轮啮入区形成局部高压,齿轮啮出区形成局部低压.随着转速的提高,高压和低压绝对值均呈增大趋势,且增速逐渐增大,表明转速对压力的影响也逐渐增大.
[1]Chernoray V,Jahanmiri M.Experimental study of multiphase flow in a model gearbox [J].Computational Methods in Multiphase Flow VI,2011,70:153-164.
[2]王清国,桃春生,杨南.汽车润滑效率及润滑油长换油期 [J].润滑油,2017,32(1):1-6.
(WANG Qing-guo,TAO Chun-sheng,YANG Nan.The automotive lubricating efficiency and long oil drain interval [J].Lubricating Oil,2017,32(1):1-6.)
[3]林银辉,臧孟炎,胡志华,等.双离合器自动变速器油轨的流场模拟及其润滑效果评价 [J].中国机械工程,2013,24(22):3052-3056.
(LIN Yin-hui,ZANG Meng-yan,HU Zhi-hua,et al.Flow field simulation and lubrication effect evaluation of an oil orbit of dual clutch automatic transmisson [J].China Mechanical Engineering,2013,24(22):3052-3056.)
[4]吴特.高速齿轮箱体内流场分析及其密封结构数值研究 [D].成都:西南交通大学,2014.
(WU Te.Analysis of flow field and numerical study of seal structure for high-speed gearbox [D].Chengdu:Southwest Jiaotong University,2014.)
[5]刘志强,曲天威,罗世辉,等.HXN3型机车齿轮箱模拟仿真研究 [J].中国铁路,2012(7):56-60.
(LIU Zhi-qiang,QU Tian-wei,LUO Shi-hui,et al.Numerical simulation of HXN3 vehicle gearbox [J].Chinese Railways,2012(7):56-60.)
[6]任崇会,魏静,马跃,等.基于动网格的齿轮箱内部流场数值模拟 [J].机械强度,2013,35(6):789-794.
(REN Chong-hui,WEI Jing,MA Yue,et al.Numerical simulation of flow field in the gearbox based on dynamic mesh [J].Journal of Mechanical Strength,2013,35(6):789-794.)
[7]Li L,Versteeg H K,Hargrave G K,et al.Numerical investigation on fluid flow of gear lubrication [J].SAE International Journal of Fuels & Lubricants,2008,1(1):1056-1062.
[8]郑鹏,汤以兴,冯喆,等.基于流固耦合的离心风机蜗壳结构分析及优化 [J].沈阳工业大学学报,2014,36(4):405-410.
(ZHENG Peng,TANG Yi-xing,FENG Zhe,et al.Structural analysis and optimization of centrifugal fan volute based on fluid-structure interaction [J].Journal of Shengyang University of Technology,2014,36(4):405-410.)
[9]梁文宏,刘凯,崔亚辉.基于有限元分析的直齿轮搅油损失计算及实验验证 [J].工程力学,2016,33(5):220-226.
(LIANG Wen-hong,LIU Kai,CUI Ya-Hui.Theoretical calculations and experimental study of spur gears churning power loss based on finite element analysis [J].Engineering Mechanics,2016,33(5):220-226.)
[10]宗凌潇,马卫华,刘韦.HXN3型机车齿轮箱漏油问题及解决方案 [J].铁道机车与动车,2014(8):22-24.
(ZONG Ling-xiao,MA Wei-hua,LIU Wei.Oil leak problem of HXN3 vehicle gearbox and the solution of it [J].Railway Locomotive and Motor Car,2014(8):22-24.)