随着计算机技术的迅猛发展,云计算技术已成为现今社会的一个研究热点和重点.云计算是在分布式计算、网格计算和并行计算等基础上发展起来的一种全新的大规模计算模式,利用虚拟技术和高速网络技术来解决大规模的大数据处理问题,有很多企业做出较大投入且获得很好的成果,如亚马逊的‘弹性云’、IBM的‘蓝云’、Google的超大搜索引擎和微软的‘Windows Azure’等.随着互联网技术的发展,互联网数据量会越来越大,对云计算技术的要求也越来越高,用户要求以最小的时间跨度来完成任务,同时企业要求尽可能带来盈利,关于云计算任务调度策略的研究成为研究重点,现在较常用的云任务调度策略主要有蚁群算法[1]、遗传算法[2]和粒子群算法[3]等启发式仿生算法及其改进算法,Min-min算法[4]等非仿生式算法及其改进算法.
企业型云计算是以盈利为目的,所以很多文献的任务调度策略中心主要是以任务完成时间和任务完成成本为优化目标.文献[5]为避免早熟现象等问题提出了一种基于负载均衡和任务时间的双适应度函数改进遗传算法;文献[6]针对传统遗传算法迭代次数多和耗时久的问题提出了一种以执行时间和执行费用为优化目标的改进遗传算法;文献[7]提出了一种考虑时间和成本约束的改进遗传算法.但是,这些文献针对未成熟收敛现象均未提出较好的改进办法,在遗传算法后期可能会出现总是淘汰接近最优解的个体或者所有个体陷入同一极值而终止算法的情况,无法达到降低任务完成时间和成本的优化目标.
本文提出了基于任务完成时间和任务完成成本的双适应度函数的改进遗传算法(time and cost genetic algorithm,TCGA),引入个体相似度概念和采用并列选择法进行选择遗传操作,尽可能保证种群多样性,同时在算法后期采用加速收敛策略加快算法的收敛速度.
1 云计算任务调度
现今社会上采用的云计算编程模式是1995年由Google公司提出的Map/Reduce模式,这种模式是把云任务分成若干个子任务,各子任务按要求随机分配给虚拟机上的资源计算节点并执行,最后将结果进行整合处理输出,各任务或子任务之间是相互独立的,在虚拟机上进行并行运算.这样可以减少任务执行时间且降低成本损耗,但各虚拟资源计算节点的任务处理性能有差异,所以各子任务完成时间不同,同时各虚拟资源计算节点完成任务的单位成本不同,产生的成本消耗也不同.
各虚拟资源计算节点单位时间完成单位任务所产生的成本损耗为单位成本.云计算采用的是按需收费、即时付费的资源服务模式,一般满足以下几个条件:
1) 为了有利于虚拟机的任务执行,云任务会被分解成若干个大小均匀的子任务,子任务会被随机地分配在不同的虚拟资源上执行;
2) 每个子任务在虚拟资源计算节点上的执行时间是可监控的、可计算的;
3) 每个虚拟资源计算节点的单位成本是可估算的、已知的.
每个计算节点完成的子任务所用的时间可表示为etcij,etcij为资源节点j执行子任务i所消耗的时间,costij为资源节点j执行子任务i的成本消耗,costj为资源节点j的单位成本,则有costij=costj·etcij.
设云任务有TASK个,子任务数为![]() 虚拟资源数为n,任务执行时间为etcij,则有
虚拟资源数为n,任务执行时间为etcij,则有
(1)
式中:task(k)_lengthi为云任务k中的子任务i的长度,i∈{1,2,…,m};mipsj为虚拟资源j的处理性能,j∈{1,2,…,n}.云计算环境下的子任务在虚拟资源中进行计算时是并行独立完成的,所以子任务在各虚拟资源中执行时间的最大值为云任务调度的执行时间花费ExecuteTime,任务完成时间CompleteTime为任务执行时间与任务传输时间之和,云任务在各虚拟资源的执行成本花费ExcuteCost与传输成本花费求和即为任务调度总成本花费CompleteCost.云任务k的执行时间为
![]()
(j∈[1,n])
(2)
云任务在虚拟资源上的传输时间为
(3)
式中,transj为虚拟资源j的传输性能.任务完成时间为任务执行时间与任务传输时间之和,即
CompleteTimek=ExecuteTimek+ttkj
(4)
云任务k的总成本花费为任务执行成本与传输成本之和,即
(5)
式中,costtj为虚拟资源j的传输成本.
2 改进遗传算法
2.1 遗传算法
遗传算法是1967年美国Michigan大学Holland教授和他的学生们受生物模拟技术启发,提出的一种基于生物基因遗传和进化机制的自适应概率优化算法.遗传算法具有高效性、高鲁棒性和实用性,发展极为迅速,自提出后,在工程技术、科学计算和社会经济等方面被大面积的引用吸收,引起了全世界范围有关学者的高度重视[8-11].
遗传算法的优点很多,但是经过多年的发展和完善,依然存在许多问题未得到解决,例如:
1) 遗传算法易陷入早熟中,迄今为止没有得到很好的解决办法;
2) 在遗传算法后期,最优解会出现左右摆动情况,导致收敛速度变慢.
2.2 编码与解码
编码是遗传算法中的一个重要步骤,也是一个首要解决的问题,与编码相对应的则是解码.遗传算法的常用编码方式较多,可分为二进制编码、浮点编码和符号编码三大类,又可分为直接编码方式和间接编码方式,采用不同的编码方式对遗传算法的执行结果有不同效果.本文采用的是资源![]() 任务编码方式,这种编码方式较为直观,操作简单易行,易于理解,不易出错,且染色体长度即基因的数量为子任务数量,每个子任务对应一个被分配到的资源.如染色体{2,3,2,1,4,3,1,2,4,3},10个子任务分配给4个虚拟资源,编号为1、2、3和4的虚拟资源上的子任务数分别为2、3、3和2,即J1:{4,7},J2:{1,3,8},J3:{2,6,10},J4:{5,9},其中,J为虚拟资源,括号内为子任务在染色体中的基因排列位置.图1为任务
任务编码方式,这种编码方式较为直观,操作简单易行,易于理解,不易出错,且染色体长度即基因的数量为子任务数量,每个子任务对应一个被分配到的资源.如染色体{2,3,2,1,4,3,1,2,4,3},10个子任务分配给4个虚拟资源,编号为1、2、3和4的虚拟资源上的子任务数分别为2、3、3和2,即J1:{4,7},J2:{1,3,8},J3:{2,6,10},J4:{5,9},其中,J为虚拟资源,括号内为子任务在染色体中的基因排列位置.图1为任务![]() 资源映射关系图.
资源映射关系图.
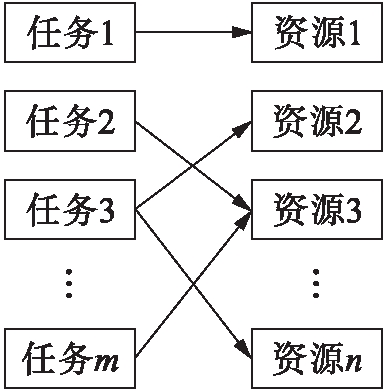
图1 任务![]() 资源映射关系
资源映射关系
Fig.1 Task-resource mapping relationship
若长度为l的染色体为{1,3,4,2,3,m-2,1,3,…,m,m-1},则任务与虚拟资源的映射关系如表1所示.
表1 映射关系
Tab.1 Mapping relationship

资源ID任务数任务ID121,7214332,5,8413︙︙︙m-11lm1l-1
2.3 适应度函数设计
适应度函数值在一定程度上决定了个体被选作为父代遗传到下一代的概率,适应度值较大的遗传到下一代的概率较大,适应度值较小的遗传到下一代的概率较小,所以适应度函数的选择很关键,本文选择的适应度函数是任务完成时间适应度函数和任务完成成本适应度函数.时间适应度函数为
(6)
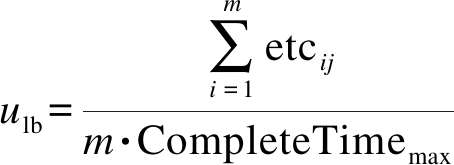
(7)
式中:ulb为任务平衡负载因子,表示虚拟资源的利用率情况,ulb越大表示虚拟资源利用率越高;CompleteTimemax为任务完成时间的最大值.成本适应度函数为
(8)
任务完成所花费时间越少的分配策略越接近最优解,运行算法所需的成本代价越低其适应度值越大.
3 遗传操作
3.1 个体相似度
传统遗传算法执行一段时间后,个体之间的相似性增大,易陷入局部最优中,本文提出个体相似度的概念来约束个体之间的相似性,加快算法的收敛速度,避免算法陷入局部最优的情况.个体染色体的长度为l,虚拟资源数为n,两个个体之间的海明码距为
(9)
其中,
(10)
相似度为
(11)
3.2 选择操作
选择操作是遗传算法的基本操作,使用比例算子进行运算,选择操作的目的是为了从当前种群中选出优秀的个体,使其有机会作为父体把优良的基因通过繁殖遗传给下一代.为了保证种群个体多样性,个体相似度大于90%的保留适应度值大的个体,适应度值小的个体被淘汰.本文主要从时间适应度函数和成本适应度函数来考虑,个体的适应度值越大,被选中作为父代繁殖遗传的可能性就越大,反之越小.种群中个体被选中的概率为
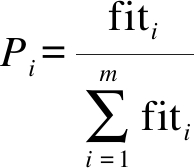
(12)
式中,fiti为个体i的适应度函数值.
本文采用最优保存策略进行选择操作,在选择操作时,把种群中所有个体的适应度函数值按照从大到小的顺序排列,首先把适应度值最大的0.5%的个体去掉,再把剩下的前10%的个体直接入选到子代种群中,剩余的个体通过轮盘赌算法进行个体选择.本文采用并列选择法对时间适应度值和成本适应度值进行选择,即按上述选择方法分别选出合适时间适应度值的个体和成本适应度值的个体,再与通过交叉和变异遗传操作生成新的个体共同组成新的子代种群.在选择这个遗传操作过程中可能会淘汰一些染色体,为了保证种群的规模,每次遗传操作开始前添加随机生成的若干个个体保持种群规模不变.
3.3 交叉和变异操作
交叉操作是按概率从种群中选出两个个体交换彼此的某个或某些位产生新的子代,交叉操作的方式有很多,如单点交叉、均匀交叉和多点交叉等.变异操作是以较小的概率将个体的某个或某些位值变异为其他等位基因生成新的个体,变异方式有基本位变异和均匀变异等.交叉和变异操作决定了遗传算法的寻优搜索能力.交叉概率公式为
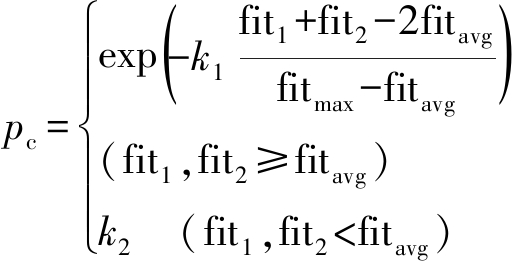
(13)
式中:fitmax为种群中的最大适应度值;fitavg为平均适应度值;fit1和fit2为种群中要交叉的个体适应度值;k1为交叉概率调节常数;k2为交叉概率常数.当交叉个体适应度值较大时(fiti≥fitavg),这时可以缩小个体交叉概率,防止较优的个体被破坏;当适应度值较小时,扩大个体交叉概率,期望可以繁殖出新的较优个体.为了提高局部寻优能力,加快收敛速度,使用变异算子微调个体的某个或某些位,变异概率公式为
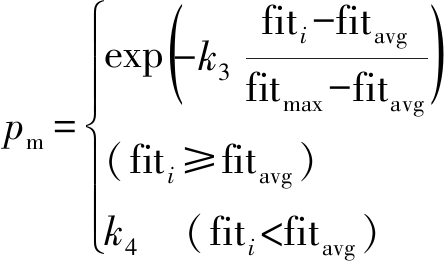
(14)
式中:fiti为种群中要变异的个体的适应度值;k3为变异概率调节常数;k4为变异概率常数.当要变异个体适应度值较大时(fiti≥fitavg),适应度值越大,变异的可能性越小,在一定程度上防止较优个体被破坏.
在遗传算法后期会出现适应度值很集中的情况,这种情况很大程度上降低了算法的收敛速度.本文提出加速收敛策略[12],当种群个体适应度值的最大值和最小值差与适应度值平均值的比值ω小于收敛阈值θ时,调节交叉概率调节常数k1和变异概率调节常数k3,使得个体的交叉和变异概率变大,加快局部搜索速度,提高算法的收敛速度.
3.4 种群初始化
设种群的大小规模为S,云任务总数为TASK,子任务数为m,虚拟资源数为n,则种群初始化可描述为:由系统随机生成S个长度为m的染色体,基因值为[1,n]之间的随机数.
3.5 算法流程
图2为算法流程图.由系统随机生成初始种群,计算种群中个体的适应度值,并按遗传操作进行执行寻找最优解,步骤如下:
1) 种群初始化.系统随机生成大小规模为S的初始种群.
2) 终止算法条件.算法迭代次数是否达到最大值或找到最优解,是则终止算法;否则继续执行.
3) 选择操作.计算种群个体适应度函数值,排列后通过最优保存策略选取前10%为下一代种群个体,采用轮盘赌方式对剩余个体进行选择操作.
4) 交叉操作.随机选取两个个体进行交叉操作生成新种群的个体.
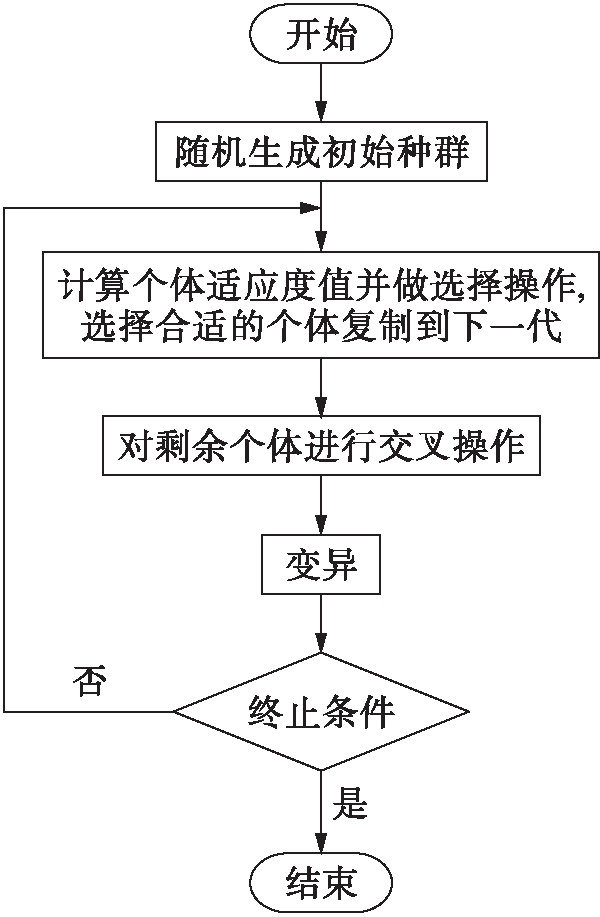
图2 算法流程图
Fig.2 Flow chart of algorithm
5) 变异操作.随机选择一个个体进行变异操作生成新种群的个体.
6) 对新生成种群个体进行判断筛选是否找到最优解,有则输出结果;无则跳转到步骤2)中.
4 仿真实验结果分析
本文采用墨尔本大学Buyya教授领导开发的CloudSim仿真模拟器对算法进行仿真模拟实验,并对实验结果进行比较分析.将本文方法与遗传算法、文献[5]中的SAIGA算法进行实验对比,分析比较各算法在不同情况下的任务完成时间、任务完成成本和收敛结果.对算法中的各参数取值进行初始化,如表2所示.
表2 参数初始化
Tab.2 Parameter initialization

参数名称取值交叉概率调节常数k15.00交叉概率常数k20.80变异概率调节常数k35.00变异概率常数k40.08收敛阈值θ0.01
算法初始条件:种群规模S取值为30,子任务数m取值为1 000,虚拟资源n取值为10,虚拟资源的单位成本costj和传输成本costtj由系统随机生成,算法的最大迭代次数设置为100.实验结果如图3~5所示.
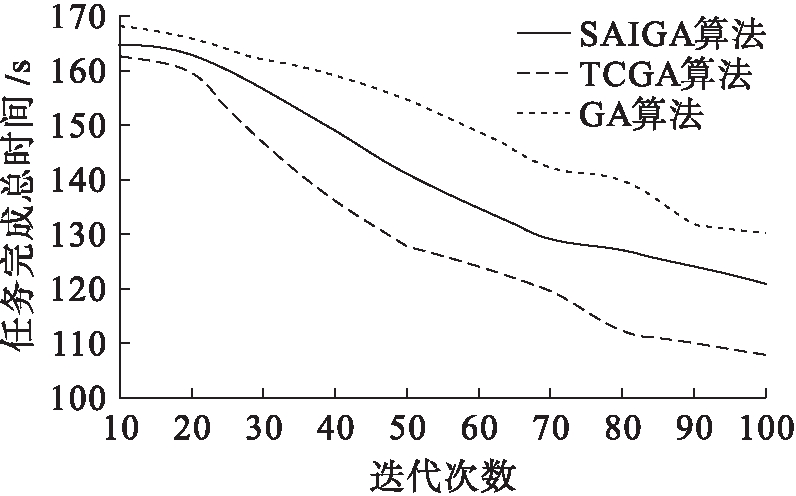
图3 任务完成时间对比
Fig.3 Comparison of task completion time
图3中总任务数量为1 000个,从图3中可以看出,在相同任务数量情况下,分别运行遗传算法、TCGA算法和SAIGA算法,在迭代次数较少时,3种算法的任务完成时间各不相同,TCGA算法花费时间最少,遗传算法花费时间最多,但是3种算法花费的时间相差较小;随着迭代次数的增多,3种算法花费的时间差距越来越大,在最大迭代次数的情况下,TCGA算法的任务完成时间比遗传算法和SAIGA算法分别降低了13%和8%.
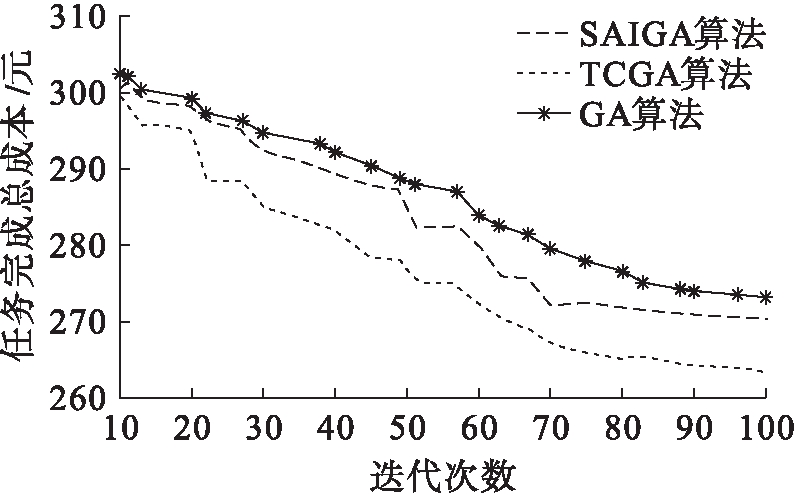
图4 任务完成成本对比
Fig.4 Comparison of task completion cost
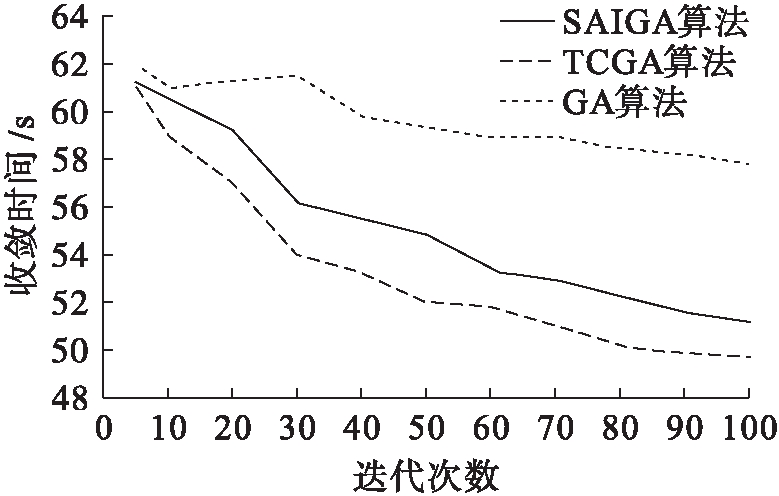
图5 收敛结果对比
Fig.5 Comparison of convergence results
图4中总任务数量为1 000个,从图4中可以看出,TCGA算法、遗传算法和SAIGA算法在算法初期,任务完成成本相差不大;随着算法迭代次数的增多,3种算法的任务完成成本会降低且降低的程度各不相同,算法之间的任务完成成本差距变大,TCGA算法的任务完成成本相比较于遗传算法和SAIGA算法分别降低了4%和3%.
图5中总任务数量为1 000个,从图5中可以看出,TCGA算法、遗传算法和SAIGA算法的收敛速度各不相同,随着迭代次数的增加,收敛所需时间差距变大,遗传算法的收敛速度最慢,TCGA算法的收敛速度更快,寻优时间最短.
综上分析可知,本文提出的双适应度函数改进遗传算法的任务完成时间更短,成本更低,收敛速度更快,寻优能力更强,能较好地完成云任务调度问题.
5 结 论
云计算调度优化策略通常是以任务完成时间和任务完成成本为优化目标,本文提出并列选择法根据适应度函数值确定选择概率完成选择操作,把任务完成时间和任务完成成本作同等地位来处理云计算任务调度的优化问题,这样能根据各自优化目标函数选出符合要求的个体,本文算法没有考虑其他因素对云任务调度过程的影响,如网络服务质量等,下一步讨论研究需要把这些因素考虑在内.
[1]聂清彬,蔡婷,王宁.改进的蚁群算法在云计算资源调度中的应用 [J].计算机工程与设计,2016,37(8):2016-2020.
(NIE Qing-bin,CAI Ting,WANG Ning.Application of improved ant colony algorithm in resource allocation of cloud computing [J].Computer Engineering and Design,2016,37(8):2016-2020.)
[2]屈迟文.基于改进遗传算法的云计算任务调度研究 [J].世界科技研究与发展,2013,35(5):616-619.
(QU Chi-wen.Research on cloud computing task scheduling based on improved genetic algorithm [J].World Sci-Tech R & D,2013,35(5):616-619.)
[3]赵莉.基于改进量子粒子群算法的云计算资源调度 [J].南京理工大学学报,2016,40(2):223-228.
(ZHAO Li.Cloud computing research scheduling based on improved quantum particle swarm optimization algorithm [J].Journal of Nanjing University of Science and Technology,2016,40(2):223-228.)
[4]郭平,李涛,李琪.一种云计算环境下的负载调度算法 [J].系统工程理论与实践,2014,34(增刊1):269-275.
(GUO Ping,LI Tao,LI Qi.A scheduling strategy on load balancing in cloud computing [J].Systems Engineering Theory & Practice,2014,34(Sup1):269-275.)
[5]刘峰,毕利,杨军.一种用于云计算资源调度的改进遗传算法 [J].计算机测量与控制,2016,24(5):202-206.
(LIU Feng,BI Li,YANG Jun.An improved genetic algorithm for cloud computing resource scheduling [J].Computer Measurement & Control,2016,24(5):202-206.)
[6]陈晓燕,姚高伟,张鲲,等.一种改进的遗传算法在云计算中的应用 [J].信阳师范学院学报(自然科学版),2015,28(3):438-441.
(CHEN Xiao-yan,YAO Gao-wei,ZHANG Kun,et al.Application of an improved genetic algorithm in cloud computing [J].Journal of Xinyang Normal University(Natural Science Edition),2015,28(3):438-441.)
[7]朱宗斌,杜中军.基于改进GA的云计算任务调度算法 [J].计算机工程与应用,2013,49(5):77-80.
(ZHU Zong-bin,DU Zhong-jun.Improved GA-based task scheduling algorithm in cloud computing [J].Computer Engineering and Application,2013,49(5):77-80.)
[8]孙晓燕,陈姗姗,巩敦卫,等.基于区间适应值交互式遗传算法的加权多输出高斯过程代理模型 [J].自动化学报,2014,40(2):172-184.
(SUN Xiao-yan,CHEN Shan-shan,GONG Dun-wei,et al.Weighted multi-output Gaussian process-based surrogate of interactive genetic algorithm with indivi-dual’s interval fitness [J].Acta Automatica Sinica,2014,40(2):172-184.)
[9]袁满,刘耀林.基于多智能体遗传算法的土地利用优化配置 [J].农业工程学报,2014,30(1):191-199.
(YUAN Man,LIU Yao-lin.Land use optimization allocation based on multi-agent genetic algorithm [J].Transactions of the Chinese Society of Agricultural Engineering,2014,30(1):191-199.)
[10]胡瑾,何东健,任静,等.基于遗传算法的番茄幼苗光合作用优化调控模型 [J].农业工程学报,2014,30(17):220-227.
(HU Jin,HE Dong-jian,REN Jing,et al.Optimal re-gulation model of tomato seedling’s photosynthesis based on genetic algorithm [J].Transactions of the Chinese Society of Agricultural Engineering,2014,30(17):220-227.)
[11]马小雨.基于自适应遗传算法的DFB激光器模糊PID温控系统 [J].沈阳工业大学学报,2017,39(4):454-458.
(MA Xiao-yu.Fuzzy PID temperature control system for DFB laser based on adaptive genetic algorithm [J].Journal of Shenyang University of Technology,2017,39(4):454-458.)
[12]袁雪莉,钟明洋.改进遗传算法的并行任务调度 [J].计算机工程与应用,2011,47(10):56-59.
(YUAN Xue-li,ZHONG Ming-yang.Parallel task scheduling algorithm using improved genetic algorithm [J].Computer Engineering and Applications,2011,47(10):56-59.)