我国特殊的地理气候条件决定了洪涝灾害具有季节性和区域性的特点.洪涝灾害的发生影响了国民经济发展,严重威胁着人民生命财产安全.灾害发生后及时对灾情严重性和可转移人数做出快速判断是灾民安置、伤患救助与食物供给的基础.建立科学、合理的预测洪水灾害应急物资需求模型对实现高效救援具有重要参考价值.
针对应急物资需求预测方法,国内外学者做了大量研究,主要集中在两大类:一类基于数理统计和案例推理技术构建预测模型;一类基于历史数据与智能优化算法构建数学模型.基于数理统计和案例推理技术方法中,Spencer使用改进的多元时间序列模型,对灾害应急物资需求进行预测[1];蔡玫等采用二型模糊集合表征群体意见,利用模糊群决策理论解决信息不完备情况下的应急物资需求预测问题[2];曾波等将传统灰色模型推广为灰色异构数据预测模型,通过灰色异构数据“核”序列建立自然灾害应急物资预测模型[3];詹沙磊等基于马尔科夫理论建立了供需不平衡环境下应急物资的分配模型,动态决策台风灾害中物资的需求预测[4];李沁鲜运用案例推理方法,通过相似案例建立灾害应急物资需求模型[5].
基于历史数据与智能优化算法构建数学模型方法中,钱枫林等在研究地震伤亡人数预测中采用BP神经网络方法,相比高斯拟合函数模型其预测精度大大提高[6];刘建华等提出了BP神经网络与聚类分析相结合的模式,对城市水灾灾情进行预测[7];程琼琼通过分析对地震灾情影响因素与灾后人员伤亡人数的关系,采用GA优化BP神经网络方法建立了地震应急物资动态预测模型[8];亢丽君采用粒子群算法对神经网络权值进行优化,实现应急物资需求预测[9];Mohammadi等创建了基于遗传算法和改进自适应粒子群算法的RBFNs方法,用于预测地震后应急物资需求量[10].
在物资需求预测研究方法中,基于数理统计方法和案例推理技术中多要引用专家经验,模型主观性较强.基于智能优化算法的物资需求模型,建立了数据到数据的非线性映射,能够客观描述受灾情况与物资需求的关系.但由于神经网络权值和阈值选取具有随机性,导致预测结果波动性较大.采用GA和PSO等智能模型优化了网络权值与阈值的选取策略,有效提高了预测的稳定性,但算法收敛速度有待提高.针对上述问题,本文建立了一种新的改进蚁群优化BP神经网络算法,基于洪涝灾害中表征受灾情况的8项主要指标,预测受灾人口转移数量.综合库存管理知识间接预测洪涝灾害中主要应急物资需求量.改进蚁群算法的使用,加快了网络的收敛速度,通过引进后代蚁群贡献因子,增加了蚁群搜索的多样性,进一步优化了BP神经网络权值与阈值的选择策略,提升了算法预测的稳定性.
1 BP神经网络与蚁群算法
1.1 BP神经网络
1986年,Rumelhart和McClelland等科学家通过模拟人脑皮层对信息的反馈机制,创建了一种多层前馈网络算法——BP神经网络.三层网络拓扑结构如图1所示.BP算法通过信息正向传递与误差反向传播,不断更新网络的权值和阈值,由正反两个过程对网络进行多次训练,直到满足最小误差为止.BP网络均方误差函数表达式为
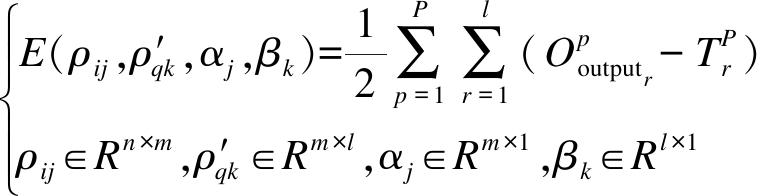
(1)
式中:n为网络输入层节点总数;m为网络隐含层节点总数;l为网络输出层节点总数;P为训练样本总组数;ρij和![]() 分别为输入层中第i个节点到隐含层中第j个节点的网络权值和隐含层中第q个节点到输出层中第k个节点的网络权值;αj和βk分别为隐含层中第j个节点对应的阈值和输出层中第k个节点对应的阈值;
分别为输入层中第i个节点到隐含层中第j个节点的网络权值和隐含层中第q个节点到输出层中第k个节点的网络权值;αj和βk分别为隐含层中第j个节点对应的阈值和输出层中第k个节点对应的阈值;![]() 为输出层中第r个节点的网络实际输出;
为输出层中第r个节点的网络实际输出;![]() 为第r个节点对应的期望输出.BP网络通过双向训练调节误差函数
为第r个节点对应的期望输出.BP网络通过双向训练调节误差函数![]() 使其满足误差要求,确定网络参数,获得稳定的网络整体结构.
使其满足误差要求,确定网络参数,获得稳定的网络整体结构.
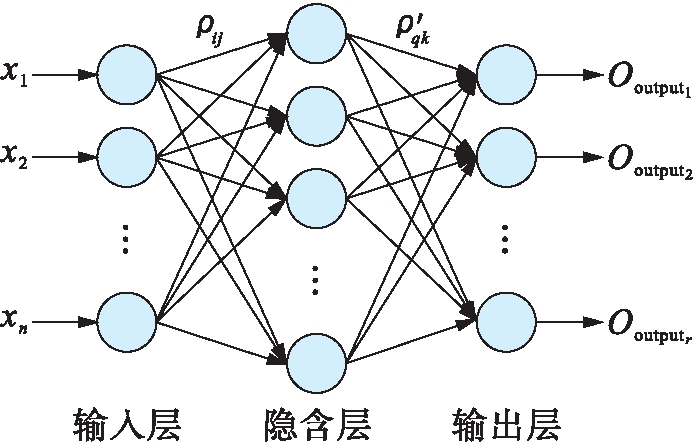
图1 BP网络拓扑结构
Fig.1 Topological structure of BP network
1.2 基本蚁群算法
蚁群算法是由Marco Dorigot通过对蚂蚁觅食行为的模拟提出的一种启发式群智能全局优化算法.个体蚂蚁在探寻食物的路径上残留一种称为信息素的分泌物,蚁群通过此种物质浓度的累积量判别食物与巢穴之间的路径长度,从而获得最短路径.蚂蚁择路策略表达式为
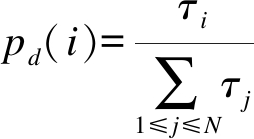
(2)
τi(t+1)=(1-ρ)τi(t)+Δτ(t)
(3)
Δτ(t)=Q/Ld
(4)
式中:τi为第i条路径上的信息素浓度;ρ为信息素挥发系数;Q为信息素增量强度;Ld为蚂蚁d在本次循环中所走路径总长度;Δτ(t)为从第t次迭代到第t+1次迭代路径择优过程中信息素的增加量.蚂蚁d在N条待选路径中依据式(2)获得的概率最大值选择下一步的觅食路径.在第t次迭代路径选择中,蚁群中所有蚂蚁选择一条完整路径之后,对经过路径上的信息素浓度按照式(3)规则进行更新.由于初始状态各条路径上信息素是相同的,故初次迭代时,蚂蚁以相同概率随机选择初始觅食路径.当蚁群在进行多次择优路径迭代后,所有蚂蚁选择相同路径或达到最大迭代次数,即获得全局最优解,该算法结束.
1.3 改进蚁群优化算法(IACO)
在经典蚁群算法中,信息素挥发系数在其迭代过程中不变.信息素挥发系数的不变性导致在初始迭代过程中没有被随机选择到的路径上的信息素逐渐消失,进一步降低了这些路径被选择的可能性.同时,非最优路径上的信息素不断积累,促使这些路径被选择的可能性增大,算法易陷入局部最优.本文提出了后代蚁群贡献因子φ(t),改进了信息素更新策略,其表达式为
τi(t+1)=(1-ρ)φ(t)τi(t)+Δτ(t)
(5)
φ(t)=exp(-t/M)
(6)
式中:φ(t)为一个单调递减的指数函数,即t值越大,φ(t)值越小;M为一个大于0的常数,表示后代蚁群信息素的贡献能力,M值越大,残留信息素浓度越低,后代蚁群贡献能力越弱.图2为贡献因子函数图像.随着蚂蚁贡献因子的引入,信息素的均匀挥发得到改善.信息素挥发浓度以指数形式增长,降低了后代蚂蚁信息素浓度的贡献.与此同时,每次循环中在最短路径上蚂蚁走的路径总长度最短,单次循环信息素浓度增加量最大.这种双向的信息素调节为最优路径上信息素浓度累积达到最大值奠定了基础,提高了蚂蚁选择最优路径的可能性,增加了蚁群全局搜索的随机性和多样性.
2 改进蚁群优化BP神经网络算法(IACO-BP)
BP神经网络初始权值和阈值的随机性是导致预测结果不稳定的主要原因.采用IACO算法获得的全局最优解作为BP网络的初始权值和阈值,既减少了神经网络对权值和阈值的修正次数,又避免了初始权值的随机性,有效提高了BP神经网络预测的精度和稳定性.算法具体过程如下:
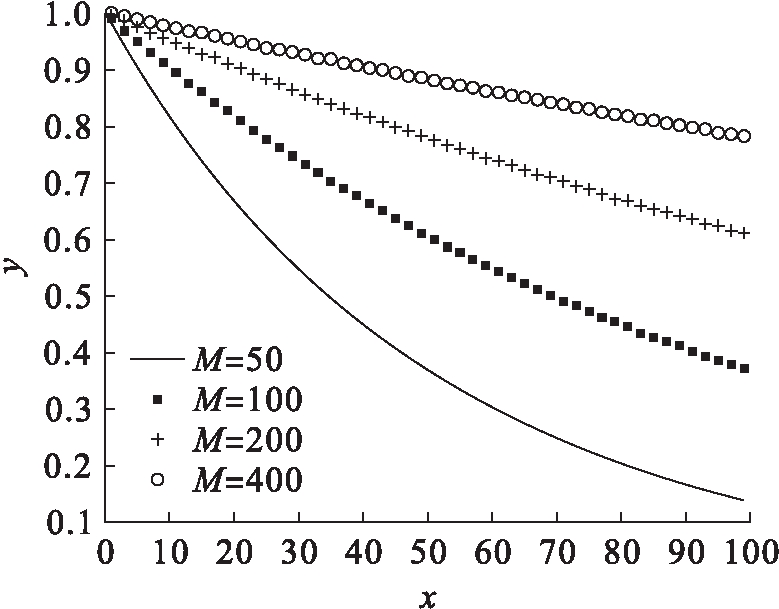
图2 贡献因子函数图像
Fig.2 Image of contributing factor function
1) 对训练样本数据集和测试样本数据集进行归一化处理,即
(7)
式中,xmax和xmin分别为训练样本数据中的最大值与最小值.
2) 建立n×m×l三层网络拓扑结构,确定n、m、l取值.
3) 初始化蚁群参数.确定蚂蚁数量C、初始信息素浓度τ0、信息素挥发系数ρ、信息素增量强度Q、后代蚁群贡献力值M、最大迭代次数qmax、神经网络待优化参数维度和每个参数的取值个数等.
4) 启动蚂蚁,每只蚂蚁根据式(2)~(6)计算信息素浓度,更新信息素.
5) 重复步骤4),直到所有蚂蚁都选择同一条路径或者达到最大迭代次数为止,转到步骤6).
6) 将改进蚁群算法找到的最优解作为BP网络的初始参数值,计算模型误差,并将误差反向传递到输出层,调整权值.重复以上过程,直到满足BP算法训练终止条件εBP或达到网络最大迭代次数![]()
7) 将测试数据进行反归一化,还原测试数据形态,其表达式为
(8)
3 洪涝灾害转移人数预测模型
本文建立了基于IACO-BP算法的洪涝灾害转移人数预测模型.选取8项洪涝灾害指标:受灾人口、最大降雨量、洪水等级、降雨等级、受灾范围、房屋倒塌数、降雨时长和预报水平作为网络输入,选取转移人数作为网络输出,对灾害中需要转移的人数进行准确预测.通过与BP、PSO-BP灾害转移人数预测模型进行对比,验证模型的有效性.
3.1 数据集
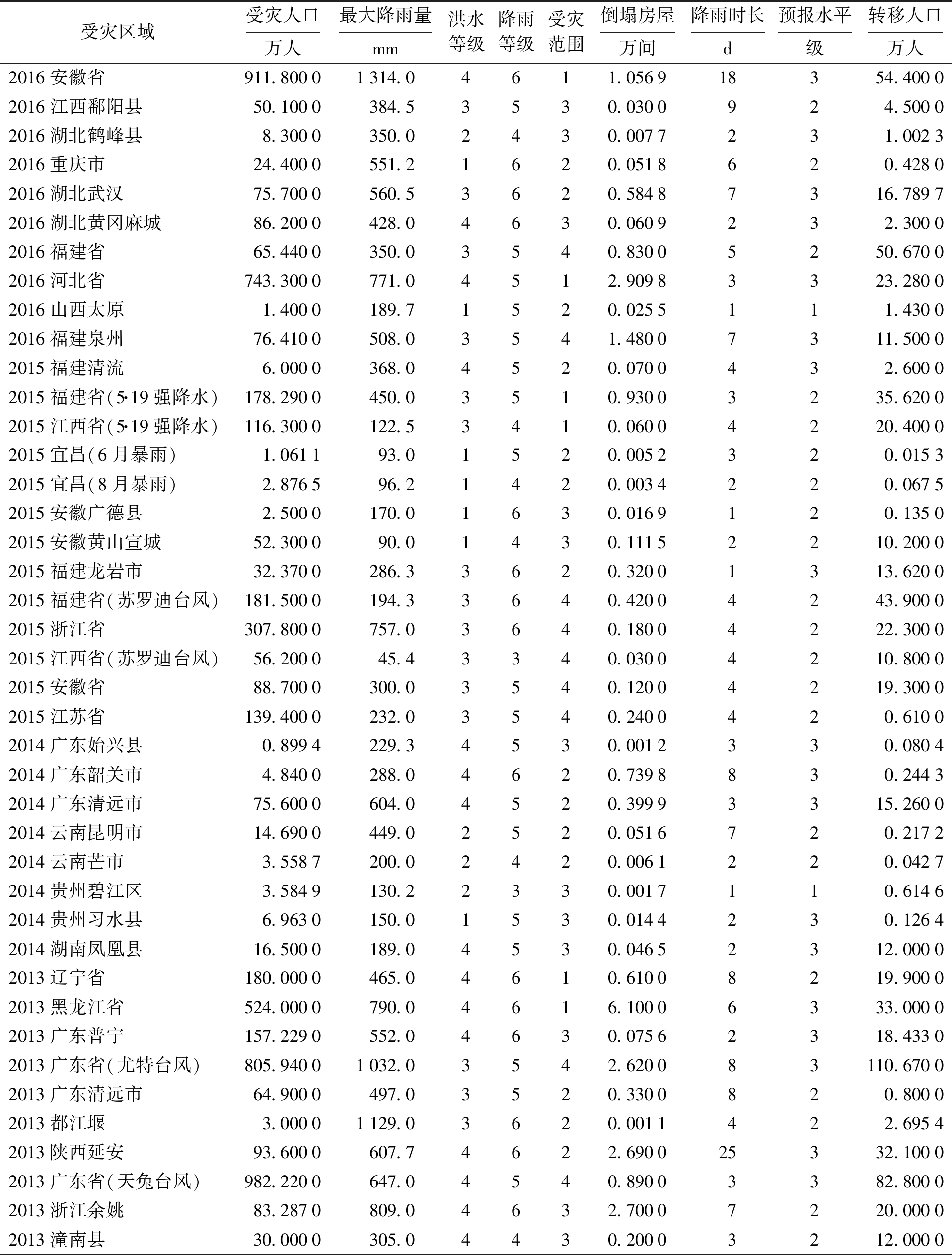
本文实验数据来源于国家水利部发布的2013~2016《中国水旱灾害公报》和历年新闻报道,对数据中的降雨量、洪水规模、预报水平进行了相应的等级划分.样本数据中的受灾范围为1~4,分别表示省、市、县及台风区域所对应的影响,样本集如表1所示.
表1 样本集
Tab.1 Set of samples
受灾区域受灾人口万人最大降雨量mm洪水等级降雨等级受灾范围倒塌房屋万间降雨时长d预报水平级转移人口万人2016安徽省911.80001314.04611.056918354.40002016江西鄱阳县50.1000384.53530.0300924.50002016湖北鹤峰县8.3000350.02430.0077231.00232016重庆市24.4000551.21620.0518620.42802016湖北武汉75.7000560.53620.58487316.78972016湖北黄冈麻城86.2000428.04630.0609232.30002016福建省65.4400350.03540.83005250.67002016河北省743.3000771.04512.90983323.28002016山西太原1.4000189.71520.0255111.43002016福建泉州76.4100508.03541.48007311.50002015福建清流6.0000368.04520.0700432.60002015福建省(5·19强降水)178.2900450.03510.93003235.62002015江西省(5·19强降水)116.3000122.53410.06004220.40002015宜昌(6月暴雨)1.061193.01520.0052320.01532015宜昌(8月暴雨)2.876596.21420.0034220.06752015安徽广德县2.5000170.01630.0169120.13502015安徽黄山宣城52.300090.01430.11152210.20002015福建龙岩市32.3700286.33620.32001313.62002015福建省(苏罗迪台风)181.5000194.33640.42004243.90002015浙江省307.8000757.03640.18004222.30002015江西省(苏罗迪台风)56.200045.43340.03004210.80002015安徽省88.7000300.03540.12004219.30002015江苏省139.4000232.03540.2400420.61002014广东始兴县0.8994229.34530.0012330.08042014广东韶关市4.8400288.04620.7398830.24432014广东清远市75.6000604.04520.39993315.26002014云南昆明市14.6900449.02520.0516720.21722014云南芒市3.5587200.02420.0061220.04272014贵州碧江区3.5849130.22330.0017110.61462014贵州习水县6.9630150.01530.0144230.12642014湖南凤凰县16.5000189.04530.04652312.00002013辽宁省180.0000465.04610.61008219.90002013黑龙江省524.0000790.04616.10006333.00002013广东普宁157.2290552.04630.07562318.43302013广东省(尤特台风)805.94001032.03542.620083110.67002013广东清远市64.9000497.03520.3300820.80002013都江堰3.00001129.03620.0011422.69542013陕西延安93.6000607.74622.690025332.10002013广东省(天兔台风)982.2200647.04540.89003382.80002013浙江余姚83.2870809.04632.70007220.00002013潼南县30.0000305.04430.20003212.0000
3.2 仿真实验
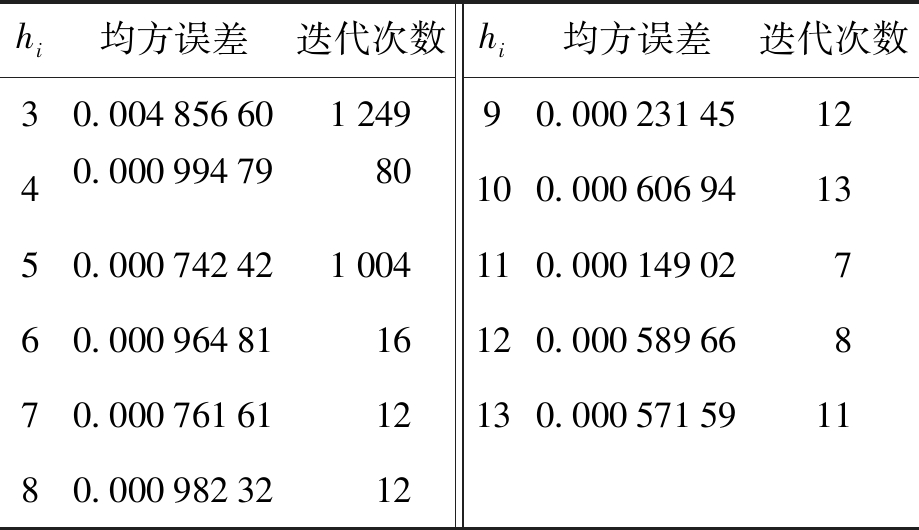
神经网络隐含层节点个数对网络预测的性能至关重要.本文依据经验公式![]() 为区间[0,10]之间的常数,获得隐含层节点数取值范围为[3,13].在试凑法实验中,当隐含层节点数h=11时,网络训练均方误差和迭代次数均最小,故神经网络拓扑结构为8×11×1.隐含层节点个数实验结果如表2所示.
为区间[0,10]之间的常数,获得隐含层节点数取值范围为[3,13].在试凑法实验中,当隐含层节点数h=11时,网络训练均方误差和迭代次数均最小,故神经网络拓扑结构为8×11×1.隐含层节点个数实验结果如表2所示.
表2 隐含层节点个数实验结果
Tab.2 Experimental results of number of hidden layer nodes
hi均方误差迭代次数30.00485660124940.000994798050.00074242100460.000964811670.000761611280.0009823212hi均方误差迭代次数90.0002314512100.0006069413110.000149027120.000589668130.0005715911
神经网络最大训练次数设为20 000次,学习速率设为0.1,期望误差设置为0.001.在改进蚁群算法中,改进蚁群待优化的BP神经网络的权值和阈值参数维度为111,每个参数值在[-1,1]中随机取20个数值,蚂蚁数量为80,信息素初始值为1,信息素挥发系数取0.1,信息素增量强度设为1,后代蚂蚁信息素的贡献值为50,蚁群最大迭代次数为800.
为了验证方法的有效性,采用相同的训练样本集和测试样本集对BP、PSO-BP和IACO-BP算法分别进行10次仿真实验验证,从网络的收敛速度和预测精度双向对比算法的优劣,结果如表3所示.
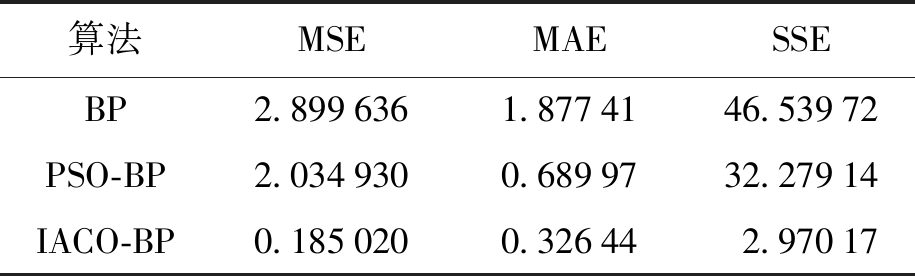
表3 模型预测精度对比
Tab.3 Comparison of prediction accuracy of various models
算法MSEMAESSEBP2.8996361.8774146.53972PSO-BP2.0349300.6899732.27914IACO-BP0.1850200.326442.97017
由表3可知,基于IACO-BP算法的灾难人口转移预测模型在10次实验的均方误差MSE平均值为0.185 02,平均绝对误差MAE平均值为0.326 44,误差平方和SSE平均值为2.970 17,均显著小于BP算法和PSO-BP算法对应的各个统计量取值.图3为MSE对比图.IACO-BP算法获得的灾难人口转移人数预测值的均方误差分别比BP和PSO-BP算法获得的均方误差小93.62%和90.91%.IACO-BP算法获得的预测值平均绝对误差分别比BP和PSO-BP算法获得的平均绝对误差小82.61%和52.69%.IACO-BP算法获得的预测值均方离差平方和分别比BP和PSO-BP算法获得的均方离差平方和小93.62%和90.80%.实验结果表明,IACO-BP算法显著提高了受灾人口转移人数的预测精度.
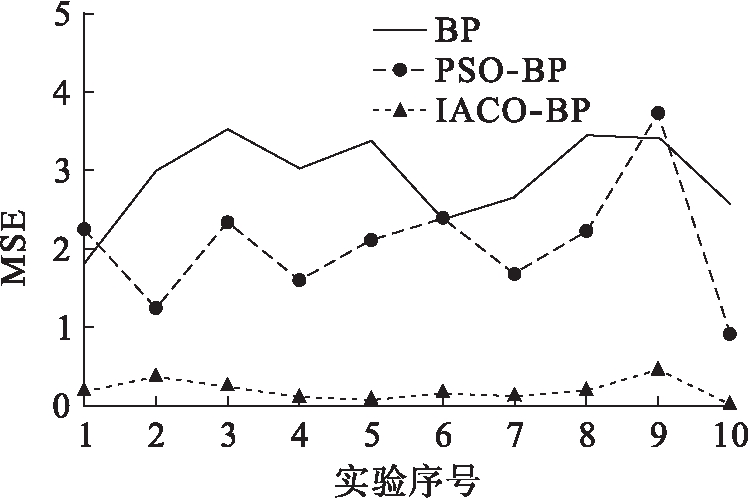
图3 MSE对比图
Fig.3 Comparison graph of MSE
由图3可知,IACO-BP算法在三种算法中波动最小,最稳定.在网络学习效率对比实验中,BP算法迭代次数为16 618次,运行时间33 s;PSO-BP算法迭代次数为4 986次,运行时间10 s;IACO-BP算法迭代次数为11次,运行时间3 s.结果表明,IACO-BP网络运行时间明显缩短,收敛速度显著提升.
4 应急物资需求预测模型
4.1 问题描述
洪涝灾害发生后,需要根据灾区受灾转移人员数量,考虑供应物资的提前期,准确预测灾区物资需求量.本文引用商业物流中安全库存理论,利用IACO-BP算法预测洪涝灾害发生后的转移人数与生活用品、非消耗救灾物品和医用药品之间的关系,建立洪涝灾害应急物资需求预测模型,间接对洪水灾害中的应急物资需求进行预测.
4.2 符号说明
记洪涝灾害发生后对灾区展开救援的初始时刻为0,以小时为单位计时,标记为T(T=0,1,2,…).洪涝灾害应急物资预测模型中使用的数学符号定义如下:Pi(T)为在时间T内的灾区转移人口数量;A1为生活用品,包括救灾粮油、饮用水、救灾食物等;A2为非消耗类救灾应急物资,包括救生船、救生圈、照明器材等;A3为医用药品,包括消毒液、防疫药物等;K为某种应急物资,如水、药品和救生船等;∂为应急物资供给的服务水平,即物资供应对灾区人民需求的满足程度;Z∂为在服务水平∂的条件下,对应的服务水平系数;U为提前期,表示连续向灾区供给物资的间隔期;αK为每个受灾人员在T-Δ时间段内对应急物资K的需求数量;![]() 为在受灾前受灾区域i内物资K的存储量;Δ为上次配送救灾物资时间;
为在受灾前受灾区域i内物资K的存储量;Δ为上次配送救灾物资时间;![]() 为时间段T-Δ内物资K已经到达灾区i的数量;
为时间段T-Δ内物资K已经到达灾区i的数量;![]() 为T时刻受灾区域i对于应急物资K的需求量,
为T时刻受灾区域i对于应急物资K的需求量,![]() 为
为![]() 的均值;
的均值;![]() 为T时刻受灾区域i对于应急物资K的单位时间平均需求量的标准差.
为T时刻受灾区域i对于应急物资K的单位时间平均需求量的标准差.
4.3 模型建立
根据提前期条件下安全库存理论,建立洪涝灾害应急物资需求模型,即
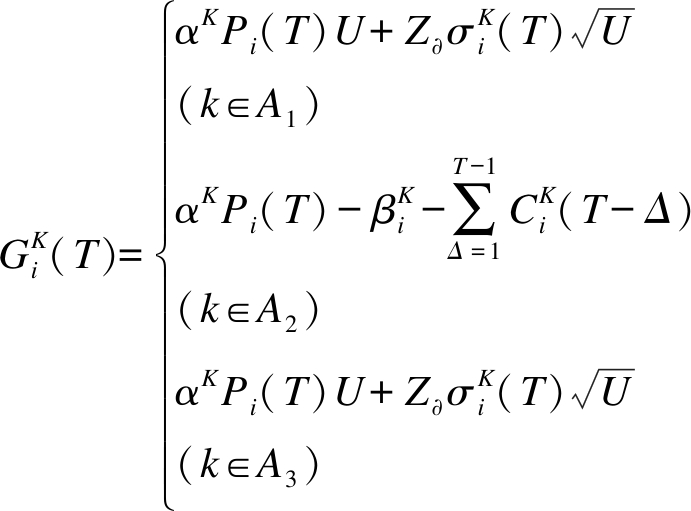
(9)
(10)
(11)
式中,![]() 为分段函数,三段函数分别描述了在T时刻第i个受灾区域对于生活用品A1、非消耗救灾物品A2和医用药品A3中的某物资K的需求量.生活用品与医用药品为连续消耗物资,需求量与提前期和库存量有关.非消耗性物资为长期使用物资,需求量与库存量和受灾后接收物资总量有关,与提前期无关.式(10)、(11)分别描述了截止到时刻T,第i个受灾区域内应急物资K需求量的标准差和均值.
为分段函数,三段函数分别描述了在T时刻第i个受灾区域对于生活用品A1、非消耗救灾物品A2和医用药品A3中的某物资K的需求量.生活用品与医用药品为连续消耗物资,需求量与提前期和库存量有关.非消耗性物资为长期使用物资,需求量与库存量和受灾后接收物资总量有关,与提前期无关.式(10)、(11)分别描述了截止到时刻T,第i个受灾区域内应急物资K需求量的标准差和均值.
4.4 算例分析
本文采用2017年吉林省永吉县暴雨灾害数据为实验数据,进行应急物资需求预测.该地洪水灾害预测指标如表4所示.
结合应急物资需求估算公式,设定相关参数为:饮用水单位需求量α1=160 mL/h,救生设施α2=0.06套,药品α3=0.05 g,服务水平系数Z∂为1.65,提前期U为6 h.基于IACO-BP算法预测的转移人口数量,采用构建的应急物资需求量预测模型,获得洪涝灾害后所需要的不同类别应急物资需求量.在洪水灾害发生的第一时间,即T=0时,![]() 其预测结果如表5所示.
其预测结果如表5所示.
表4 灾害预测指标
Tab.4 Prediction indicators of disasters

受灾区域受灾人口万人最大降雨量mm洪水等级降雨等级受灾范围倒塌房屋万间降雨时长d预报水平级吉林永吉县263092530.7523
表5 预测结果
Tab.5 Prediction results

转移人数万人饮用水(103L)救生设施套药品盒767.2420021000
5 结 论
本文提出了改进蚁群优化BP神经网络算法,基于洪涝灾害中反映受灾程度的8个主要因素,对洪涝灾害转移人数进行预测,根据转移人数与物资需求量之间的关系,建立应急物资需求量预测模型,应用于洪涝灾害物资需求测试.结果表明:基于IACO-BP神经网络算法有效解决了BP网络易陷入局部极小值的问题,与BP、PSO-BP网络算法相比,迭代次数和运行时间明显减少,预测精度和稳定性显著提高.
[1]Spencer S,Evans R,Allen T,et al.A multivariate time series approach to modeling and forecasting demand in the emergency department [J].Journal of Biomedical Informatics,2009,42(1):123-139.
[2]蔡玫,曹杰.应急物资需求量的二型模糊集合预测方法 [J].中国安全科学学报,2015,25(9):165-170.
(CAI Mei,CAO Jie.A type-2 fuzzy set based approach to predicting emergency material demand [J].China Safety Science Journal,2015,25(9):165-170.)
[3]曾波,孟伟,刘思峰,等.面向灾害应急物资需求的灰色异构数据预测建模方法 [J].中国管理科学,2015,23(8):84-91.
(ZENG Bo,MENG Wei,LIU Si-feng,et al.Prediction modeling method of grey isomerism data for calamity emergency material demand [J].Chinese Journal of Management Science,2015,23(8):84-91.)
[4]詹沙磊,傅培华,李修琳,等.基于马尔科夫决策的应急物资动态分配模型 [J].控制与决策,2018,33(7):1312-1318.
(ZHAN Sha-lei,FU Pei-hua,LI Xiu-lin,et al.Dynamic programming approach for relief goods allocation based on Markov decision [J].Control and Decision,2018,33(7):1312-1318.)
[5]李沁鲜.基于需求分析的灾害应急物资配送问题研究 [D].兰州:兰州交通大学,2013.
(LI Qin-xian.Study on disaster emergency material distribution based on demand analysis [D].Lanzhou:Lanzhou Jiaotong University,2013.)
[6]钱枫林,崔健.BP神经网络模型在应急需求预测中的应用——以地震伤亡人数预测为例 [J].中国安全科学学报,2013,23(4):20-25.
(QIAN Feng-lin,CUI Jian.Application of BP neural network model in emergency demand forecasting:a case study of earthquake casualty prediction [J].China Safety Science Journal,2013,23(4):20-25.)
[7]刘建华,张正,吴洁明.基于BP神经网络的城市水灾灾情预测模型 [J].计算机工程与设计,2005,26(3):699-701.
(LIU Jian-hua,ZHANG Zheng,WU Jie-ming.City flood forecast model based on BP network [J].Computer Engineering and Design,2005,26(3):699-701.)
[8]程琼琼.基于GA的BP神经网络的地震应急物资需求预测 [D].成都:西南财经大学,2016.
(CHENG Qiong-qiong.Earthquake emergency material demand forecast based on BP neural network of ge-netic algorithm [D].Chengdu:Southwestern University of Finance and Economics,2016.)
[9]亢丽君.粒子群优化BP神经网络在应急物资需求预测中的应用研究 [D].兰州:兰州交通大学,2013.
(KANG Li-jun.Research on application of particle swarm optimization BP neural network in forecasting emergency supplies demand [D].Lanzhou:Lanzhou Jiaotong University,2013.)
[10]Mohammadi R,Ghomi S M T,Zeinali F.A new hybrid evolutionary based RBF networks method for forecasting time series:a case study of forecasting emergency supply demand time series [J].Engineering Applications of Artificial Intelligence,2014(36):204-214.