随着我国钢结构建筑的快速发展,尤其近几年装配式建筑的兴起,出现了大量左右梁高不同非标准框架结构.在框架结构中,梁柱通过节点组合在一起.节点作为一种媒介,实现力和弯矩从一个杆件传递到另一个杆件.
传统的钢框架分析和设计一般假定梁与柱的连接或者是刚性连接,或者是理想铰接,然而实际节点的刚度是处于二者之间的半刚性连接.半刚性连接节点与刚性、铰接节点相比,具有一定的抗弯承载能力和变形能力,是抗震性能比较优越的节点连接形式.目前,国内外研究学者对半刚性连接的研究现状主要集中在两个方面:一是半刚性连接计算方法的研究,通过建立既简单又准确实用的表达方式来反映连接的剪力和剪切角之间的关系[1-6];二是在试验研究的基础上获得半刚性节点的动力性能和静力性能[7-14].半刚性节点的概念己被土木工程界所普遍接受,美国钢结构设计规范和欧洲钢结构设计规范都己将半刚性节点列入到规范条文中.我国《钢结构设计规范》(GB 50017-2003)第3.2.7条规定了“梁柱半刚性连接是有限的转动刚度,在承受弯矩的同时产生相应的转角,在内力分析时必须确定连接的弯矩![]() 转角特性,以便考虑变形的影响”.
转角特性,以便考虑变形的影响”.
为了改善钢结构框架节点的力学性能,提高整体结构的抗震性能,本文提出了一种新型的半刚性连接节点形式即外加强环式连接节点.这种节点在构造上是将外加强环板通过角焊缝直接焊接到柱壁上,梁上的荷载通过外加强环板传递到柱壁上,在梁翼缘拉力的作用下,节点域除了剪切变形外,还可能发生柱壁的局部变形.通过试验及理论研究验证了该类节点具有良好的变形能力和抗震性能[15].但目前还不明确外加强环式节点中左右梁高不同的非标准形式节点的力学性能以及各设计参数的影响.因此,本文利用有限元分析方法对外加强环式左右梁高不同的3维空间钢框架节点的力学性能进行系统研究,考察了左右梁高比、柱壁厚度、柱的轴压比、梁翼缘及外环板厚度等几何参数对外加强环式节点的承载力和刚度的影响,为该类异形节点设计提供理论基础.
1有限元模型
1.1 外加强环非标准型节点概述
本文采用有限元软件ABAQUS对圆形钢管柱-H型左右梁高不同非标准外加强环式节点进行弹塑性力学研究,节点结构如图1所示(单位:mm),分析模型的具体几何尺寸如表1所示,其中,hs为外加强环板的宽度,ts为外加强环板的厚度,hf为梁腹板高度.主要参数包括:左右H型钢梁高度比β=(hf高+2tf高)/(hf矮+2tf矮)(表1中A系列模型),圆钢管柱壁厚度tc(表1中B系列模型),H型梁翼缘厚度tf(表1中C系列模型),以及柱子的轴压比η(表1中D系列模型)等.钢管柱长度H、梁长度L、梁翼缘宽bf、腹板厚度tw以及钢管柱直径D等保持不变.试验研究结果表明,当较矮的H型钢梁与圆形钢管采用外加强环板连接时,下翼缘采用半包柱形式,其力学性能改善效果较好,因此,本文的所有模型均采用半包柱形式,即α为180°.
1.2 网格划分及材料特性
有限元模型均采用S4R壳单元,为了保证计算精度,减少计算时间,在节点核心区域网格划分较密,其余部分网格较疏.建模分析时未考虑焊缝以及焊接残余应力影响.典型的有限元模型如图2所示.
外加强环式节点各构件(梁、柱及外加强环板)材料均采用Q345级钢材,屈服应力fv为345 MPa,弹性模量E为205 GPa,泊松比v为0.3,材料本构模型采用两折线随动强化模型,强化段切线模量Et=0.01E.
1.3 边界条件
有限元分析模型的边界条件及加载方式如图3所示.在柱脚处约束水平两个方向及竖直方向的平动,柱顶处约束水平两个方向的平动,左右梁端部约束水平两个方向的平动以及绕梁纵向的转动.加载方式为:首先在柱顶部施加一定的轴向压力,然后再在左右梁端部同时施加上下反对称的竖向位移,直至节点达到破坏,观察节点域的应力分布与剪切变形情况,并对节点域的力学性能进行评价.
1.4 节点域的受力状态
为了更好地把握外加强环式节点域的弹塑性性能,便于数据整理,详细分析节点域的受力状态,如图4所示.
由于左右梁高不同,与标准形式节点域相比,异形节点域由2个部分组成,分别为上核心区和下核心区,对于上核心区的剪力计算公式为
(1)
下核心区的剪力计算公式为
(2)
核心区的平均剪力计算公式为
(3)
式中:b1M和b2M分别为两侧梁端的弯矩值;cQU和cQL分别为节点域的剪力值;db1和db2分别为节点域的高度.
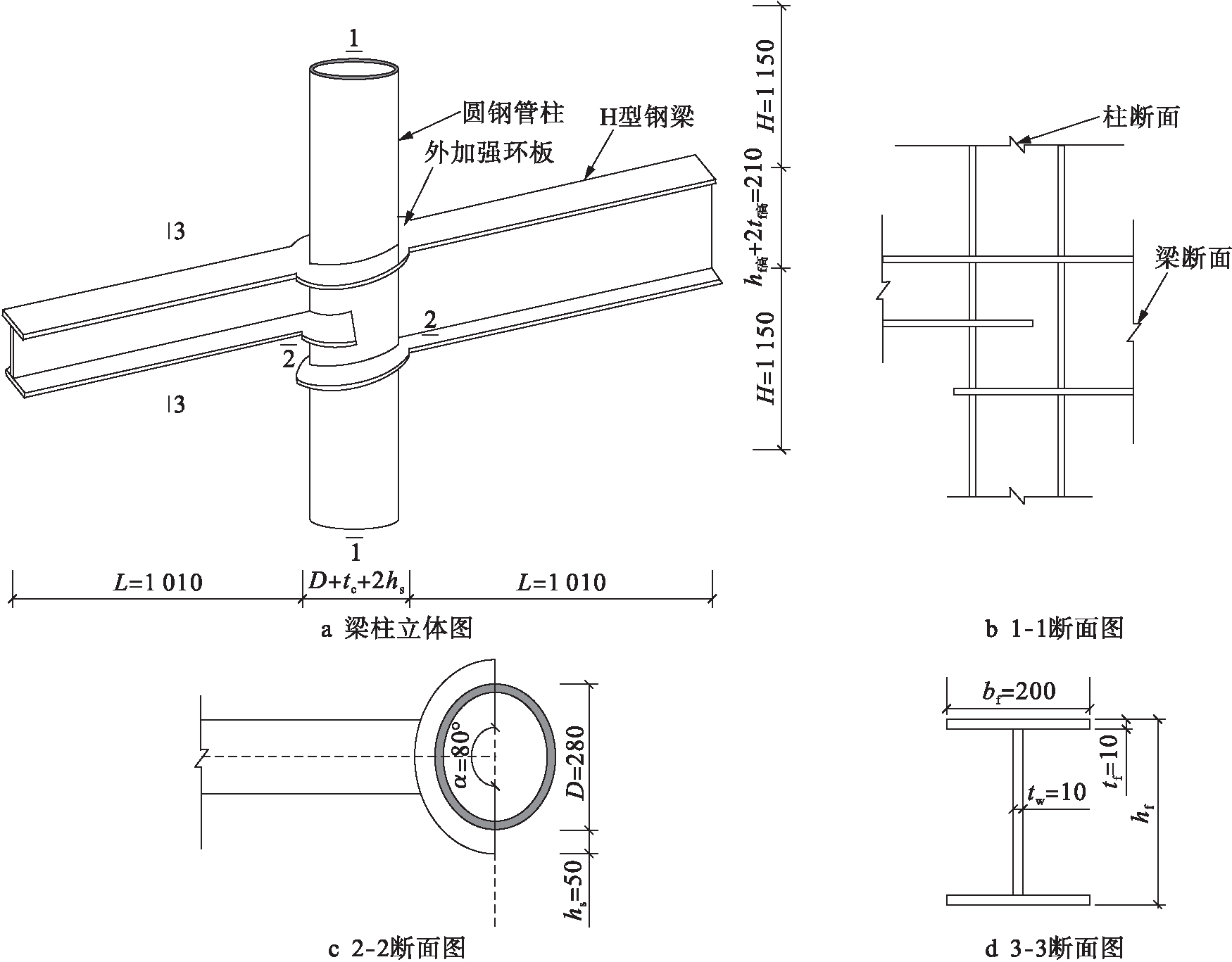
图1 圆钢管柱-H型钢梁外环板式异形节点
Fig.1 Circular hollow steel column-H shaped steel connected by irregular joints
表1 节点模型的尺寸参数
Tab.1 Dimension parameters for joint model
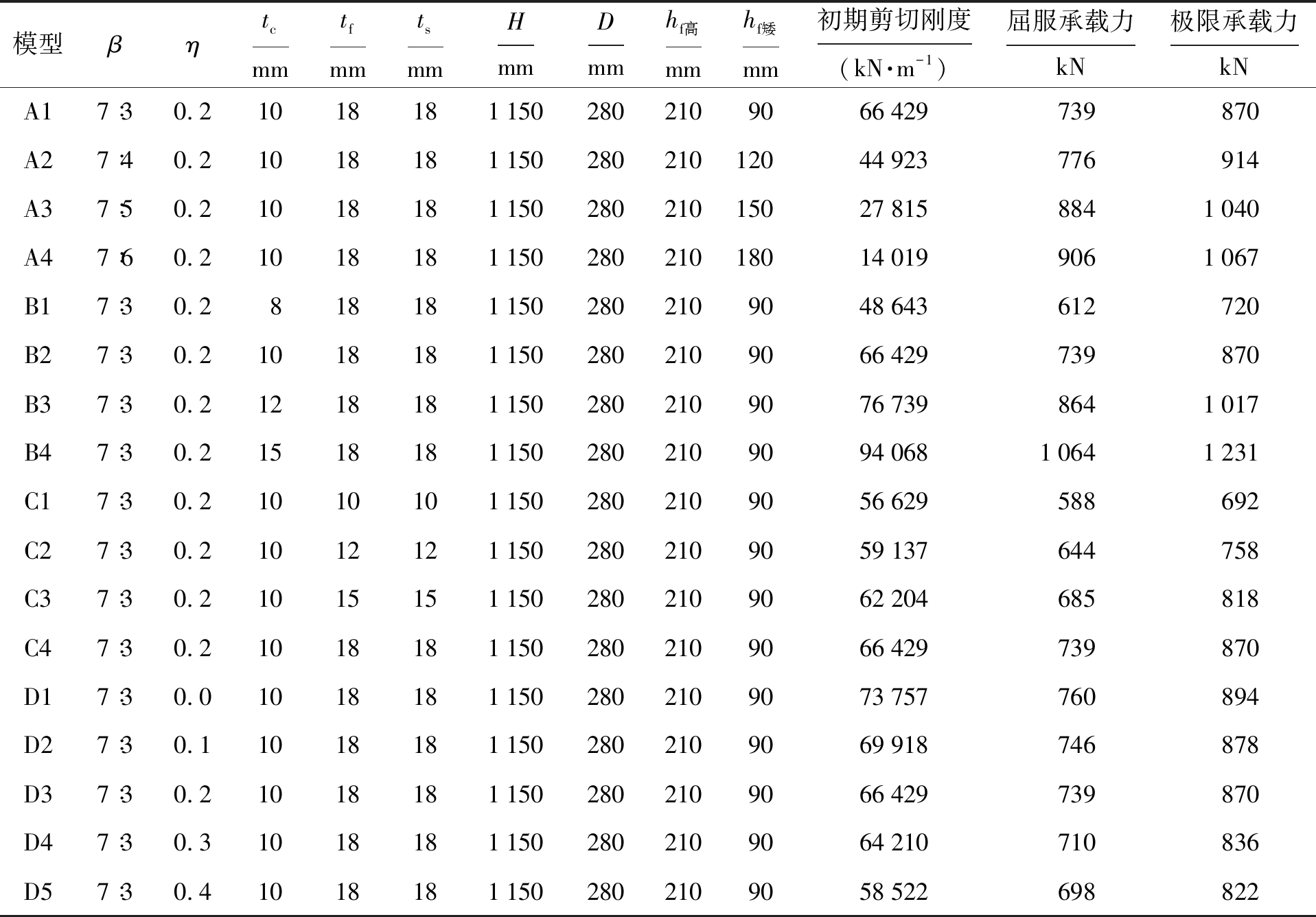
模型βηtcmmtfmmtsmmHmmDmmhf高mmhf矮mm初期剪切刚度(kN·m-1)屈服承载力kN极限承载力kNA17∶30.210181811502802109066429739870A27∶40.2101818115028021012044923776914A37∶50.21018181150280210150278158841040A47∶60.21018181150280210180140199061067B17∶30.28181811502802109048643612720B27∶30.210181811502802109066429739870B37∶30.2121818115028021090767398641017B47∶30.21518181150280210909406810641231C17∶30.210101011502802109056629588692C27∶30.210121211502802109059137644758C37∶30.210151511502802109062204685818C47∶30.210181811502802109066429739870D17∶30.010181811502802109073757760894D27∶30.110181811502802109069918746878D37∶30.210181811502802109066429739870D47∶30.310181811502802109064210710836D57∶30.410181811502802109058522698822

图2 异形节点有限元模型
Fig.2 Finite element model for irregular joints
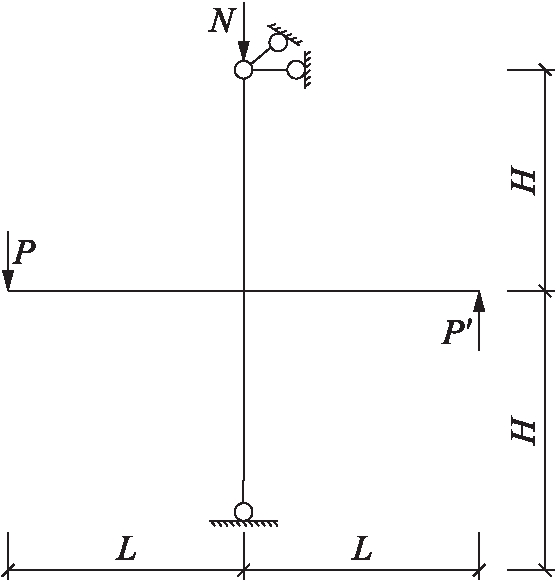
图3 框架边界条件及加载方式
Fig.3 Boundary condition and loading mode of frame
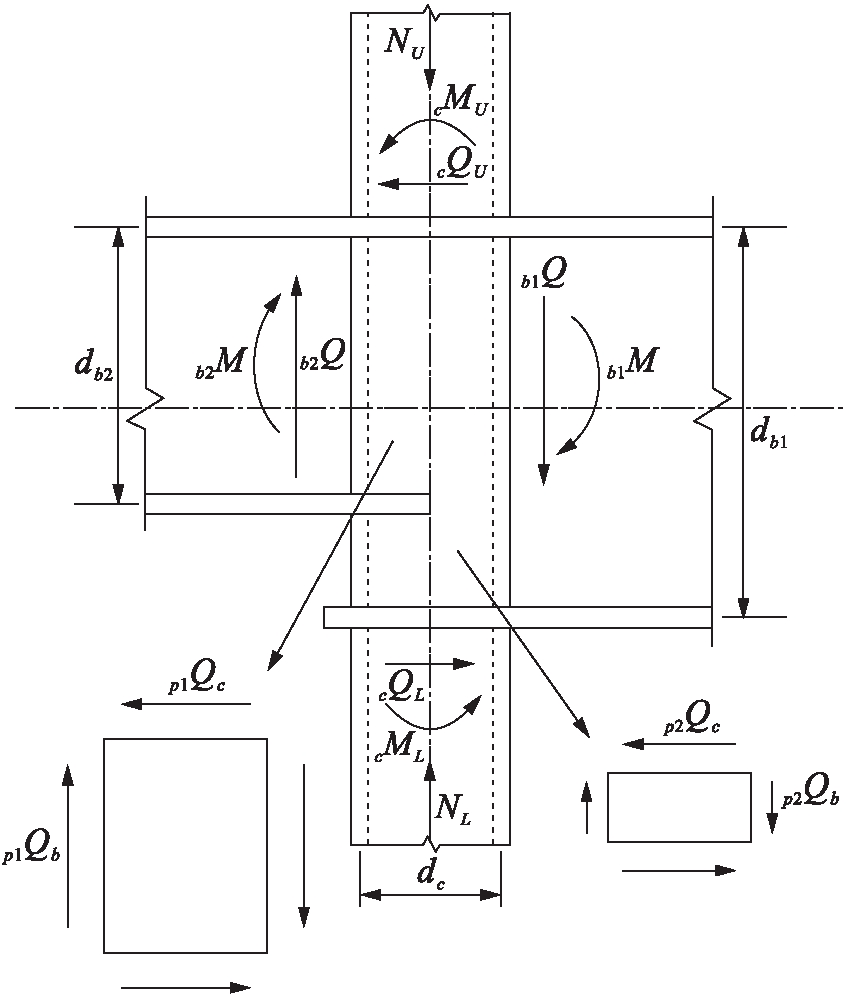
图4 节点域的受力状态
Fig.4 Force states of panel zone
对于任意一个承受剪力作用的节点域,在节点剪力的作用下,节点的剪切变形如图5所示,其中,α1为柱轴线与竖直向的夹角,α2为小梁轴线与水平方向的夹角,节点域的剪切角γ计算公式为
(4)
核心区的平均剪切角计算公式为
(5)
式中,γ1和γ2分别为与较矮一侧梁等高的节点域剪切变形和较高一侧梁对应的节点域减去较矮一侧梁对应的节点域后剩余节点域的剪切变形.
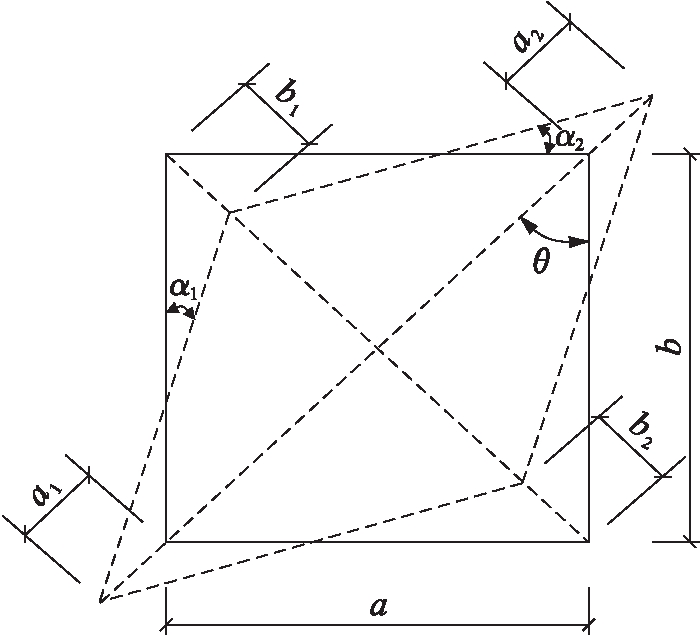
图5 节点域剪切变形示意图
Fig.5 Schematic shear deformation of panel zone
2 设计参数对节点力学性能的影响
2.1 左右梁高比对节点力学性能的影响
为了便于考察左右梁高比对外加强环节点力学性能的影响,其他参数不变,改变左右梁高比β为7∶3、7∶4、7∶5、7∶6,根据四种异形节点(A系列模型)的有限元结果,利用上述节点域剪力和剪切角计算公式(3)、(5)整理得剪力V-剪切角γ曲线,如图6所示.由图6可知,随着左右梁高比的增加,节点域的初期剪切刚度有所增加,但进入弹塑性后承载能力下降.
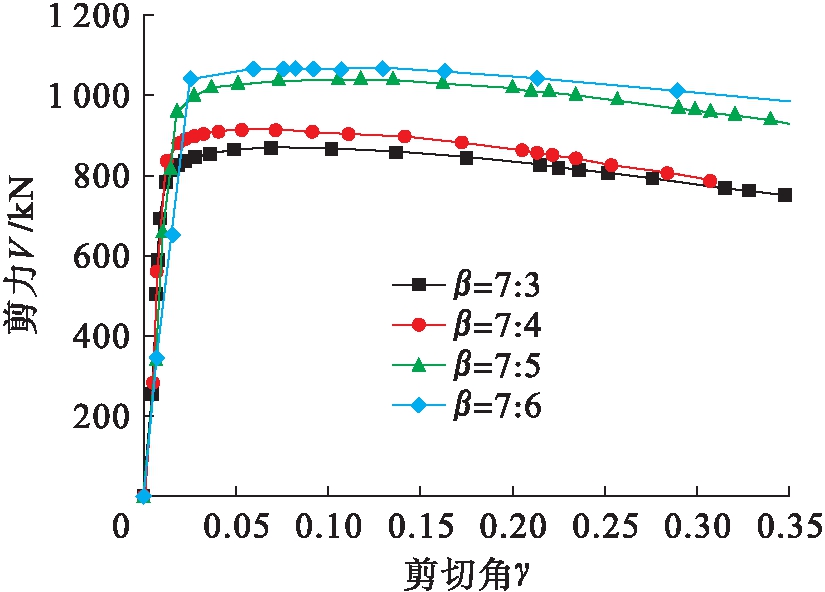
图6 左右梁高比的影响
Fig.6 Effect of left-right beam height ratio
2.2 柱壁厚度对节点力学性能的影响
为了探明柱壁厚度对节点域承载力的影响,其他参数不变,改变柱壁厚度tc为8、10、12和15 mm,四种B系列节点剪力V-剪切角γ曲线对比如图7所示.由图7可知,随着柱壁厚度的增加,节点域的初期剪切刚度变化不大,进入弹塑性后节点的承载能力显著增加,并且最大承载力增幅达70%以上.
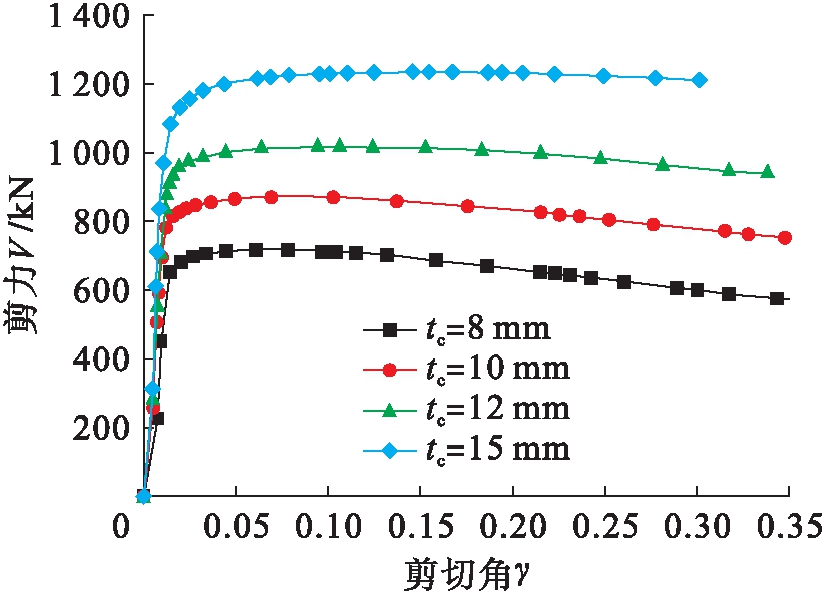
图7 柱壁厚度的影响
Fig.7 Effect of column wall thickness
2.3 梁翼缘板厚度对节点力学性能的影响
为了探明梁翼缘板厚度对节点域承载力的影响,其他参数不变,改变梁翼缘板厚度tb为10、12、15和18 mm,四种模型C系列节点剪力V-剪切角γ曲线对比如图8所示.由图8可知,随着梁翼缘板厚度的增加,节点域的初期剪切刚度变化不大,但是节点进入弹塑性后承载能力显著增加,最大增幅达30%以上.
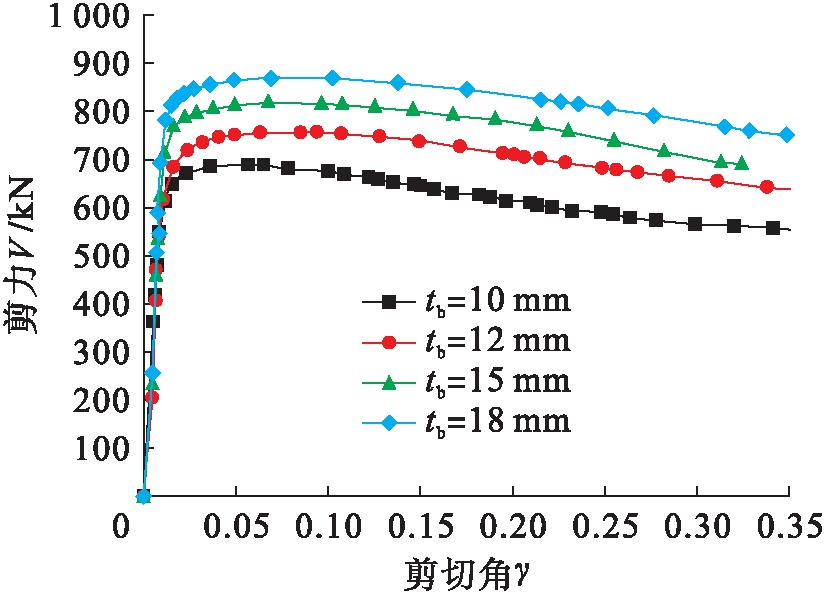
图8 梁翼缘板厚度的影响
Fig.8 Effect of beam flange thickness
2.4 柱轴压比对节点力学性能的影响
为了探明轴压比对节点域力学性能的影响,对轴压比η从0增加到0.4五种模型D系列节点剪力V-剪切角γ曲线进行比较分析,结果如图9所示.由图9可知,随着轴压比的增加,虽然初期剪切刚度变化较小,但最大抗剪承载力逐渐减小,减少约10%,并且达到最大抗剪承载力后,承载力下降速度随着轴压比的增加而变快.
2.5 节点域附近应力分布及变形
为了更详细了解外加强环式节点的应力分布及变形形态,以A系列左右梁高不同的四种模型节点为例,当节点域剪切角达到0.2时,应力分布和变形如图10所示.由图10可知,在外荷载作用下,梁与柱节点域附近产生了较高的应力,并且随着β的减小,高应力分布范围扩展到整个节点域以及上下柱的钢管壁.节点域的变形主要集中在下节点域核心区,随着β的减小,下节点域核心区的变形逐渐舒展.
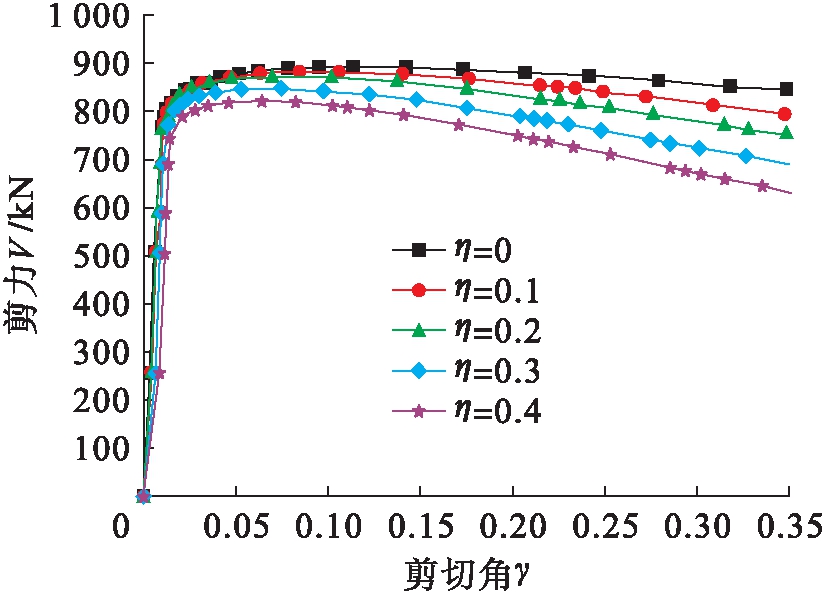
图9 轴压比的影响
Fig.9 Effect of axial compression ratio
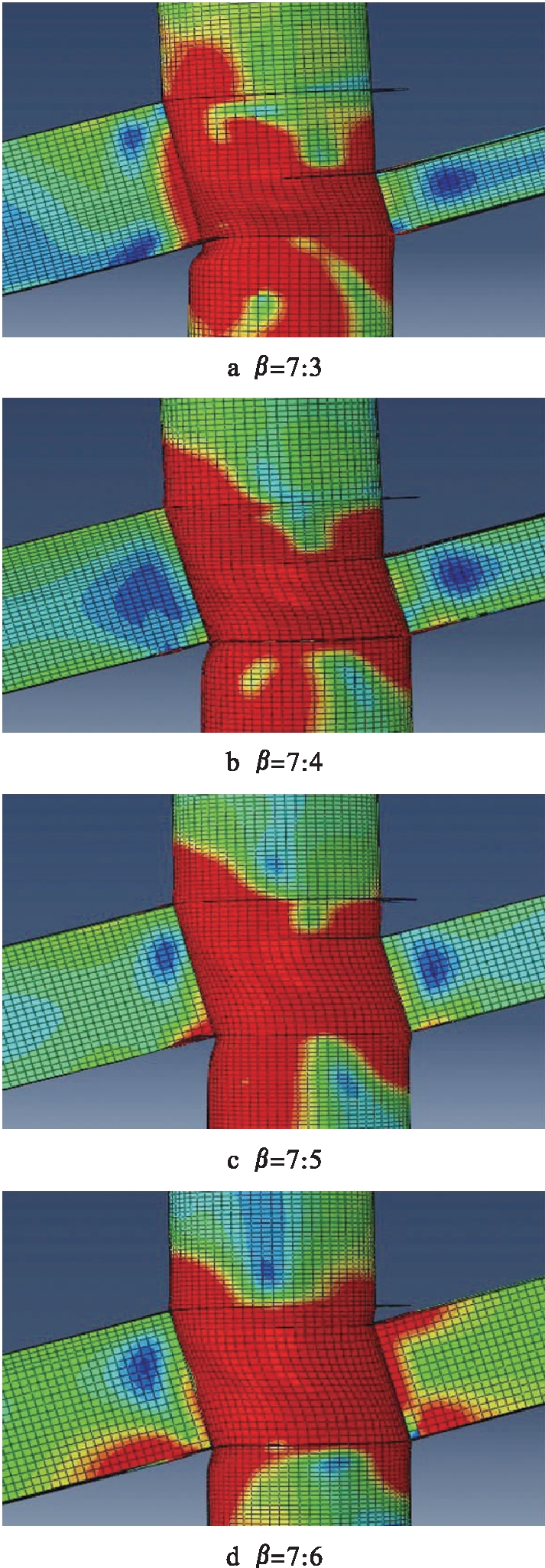
图10 剪切角为0.2时异形节点的应力分布及变形
Fig.10 Stress distribution and deformation of irregular joints with shear angle of 0.2
3 结 论
本文通过分析得出以下结论:
1) 随着左右梁高度比的增加,节点域的抗剪承载力降低,初期剪切刚度增加;
2) 增加柱壁厚度,节点域的初期剪切刚度变化较小,但抗剪承载力增加显著,最大增幅达70%;
3) 增加翼缘厚度,节点域的初期剪切刚度变化不大,但抗剪承载力增加显著,最大增幅达30%;
4) 随着轴压比的增加,节点域的抗剪承载力降低,但是刚度变化不大.
[1]Patel K V,Chen W F.Analysis of a fully bolted moment connection using NONSA P [J].Computers and Structures,1985(3):134-139.
[2]孙利骄.半刚性钢框架弱轴端板连接节点的性能分析 [D].广州:华南理工大学,2012.
(SUN Li-jiao.Connection performance research of semi-rigid beam-to-column weak axis end-plate connections in steel frames [D].Guangzhou:South China University of Technology,2012.)
[3]刘伟.半刚性连接钢框架设计理论与方法——面向直接分析设计 [D].南京:东南大学,2016.
(LIU Wei.The design theory and method of semi-rigid steel frame-based on the direct analysis design [D].Nanjing:Southeast University,2016.)
[4]孙建鹏,李青宁.半刚性连接钢框架静力分析的精细传递矩阵法 [J].沈阳工业大学学报,2012,34(5):596-600.
(SUN Jian-peng,LI Qing-ning.Mechanical transfer matrix method for static analysis of semi-rigid steel frames [J].Journal of Shenyang University of Technology,2012,34(5):596-600.)
[5]杨璐,陈虹.梁端翼缘扩大型梁柱节点受力性能 [J].沈阳工业大学学报,2017,39(4):459-463.
(YANG Lu,CHEN Hong.Mechanical performance of beam-column joint with widened beam flange [J].Journal of Shenyang University of Technology,2017,39(4):459-463.)
[6]韩明岚,王燕,董建莉.梁翼缘削弱式钢框架考虑节点域剪切变形的力学性能 [J].建筑钢结构进展,2013,15(1):22-28.
(HAN Ming-lan,WANG Yan,DONG Jian-li.Study on mechanical behavior of steel frames with reduced beam flanges considering shear deformation of panel zones [J].Progress in Steel Building Structures,2013,15(1):22-28.)
[7]狄思凡.半刚性节点刚度及对钢框架结构性能的影响研究 [D].南京:南京林业大学,2013.
(DI Si-fan.Semi-rigid joint stiffness of influence study on the structure properties of the steel frame [D].Nanjing:Nanjing Forestry University,2013.)
[8]王秀丽,邹磊.带支撑的钢框架梁柱节点的力学性能研究 [D].兰州:兰州理工大学,2012.
(WANG Xiu-li,ZOU Lei.Study on seismic design method and dynamic performance of space steel pipe truss structure [D].Lanzhou:Lanzhou University of Techonogy,2012.)
[9]王灿.半刚性连接钢框架结构动力特性与地震响应研究 [D].石家庄:石家庄铁道大学,2015.
(WANG Can.The dynamic and seismic analysis of steel frame with semi-rigid connections [D].Shijia-zhuang:Shijiazhuang Tiedao University,2015.)
[10]杨卫忠,王茜.钢结构半刚性连接弯矩![]() 转角关系模型研究 [J].郑州大学学报,2015,47(1):115-118.
转角关系模型研究 [J].郑州大学学报,2015,47(1):115-118.
(YANG Wei-zhong,WANG Qian.The analysis of entire elastic plastic process of a beam with one degree of indeterminacy under uniformly-distributed load [J].Journal of Zhengzhou University,2015,47(1):115-118.)
[11]翁庆莲.钢框架梁柱T型钢连接节点的本构模型研究 [D].南宁:广西大学,2014.
(WENG Qing-lian.Research on the constitutive mo-del of steel beam-to-column T-sub connections [D].Nanning:Guangxi University,2014.)
[12]汲小娟.半刚性连接钢框架的受力性能研究 [D].邯郸:河北工程大学,2013.
(JI Xiao-juan.Research on mechanical properties of semi-rigid connected steel frame [D].Handan:Hebei University of Engineering,2013.)
[13]孙希.左右梁高不同的钢结构异形节点抗震性能研究 [D].沈阳:沈阳建筑大学,2013.
(SUN Xi.Study on seismic performance of steel panel zones at the connection of steel column and beams with different depth [D].Shenyang:Shenyang Jianzhu University,2013.)
[14]孙章腾,雷劲松.半刚性节点连接钢框架的抗震性能研究 [J].平顶山学院学报,2016,31(2):34-38.
(SUN Zhang-teng,LEI Jin-song.The research on seismic performance of semi-rigid nodes connection in steel frame structure [J].Journal of Pingdingshan University,2016,31(2):34-38.)
[15]隋伟宁,王占飞,白雪,等.外加强环式箱型截面钢柱-H型钢梁异型节点抗震性能研究 [J].世界地震工程,2016,32(4):17-24.
(SUI Wei-ning,WANG Zhan-fei,BAI Xue,et al.Study on seismic behavior of steel ring-H-beam girder with special reinforced annular box cross section [J].World Earthquake Engineering,2016,32(4):17-24.)