长期以来，复杂、非线性且具有不确定性的摩擦环节是众多机械、控制界学者研究伺服系统的一大障碍.对于高速高精度数控机床进给伺服系统而言，摩擦环节成为了提高系统性能的瓶颈，其使系统响应出现爬行现象，产生极大的跟踪误差，从而降低了伺服系统的性能.研究表明，交流伺服系统的动态性能与采用的控制策略有直接关系.传统控制策略、智能控制策略之间组合形成的复合控制以其良好的控制性能和易于实现的特点，为进一步提高伺服系统性能和寻求具有更强鲁棒性的控制策略提供了一条崭新的途径.本文结合PID控制技术和模糊控制技术，以期改善与提高伺服系统对外界干扰、参数动态变化的自调整适应能力.同时，利用遗传算法与模糊控制复合技术补偿数控交流伺服系统的摩擦，使系统的稳态跟踪精度和动态特性能够保持良好状态[1-3].
1 数控进给伺服系统数学模型
根据数控进给伺服系统结构特点，将系统分为伺服控制系统和机械进给传动系统.为了降低建模的复杂程度，先将两系统分别建模，通过转角将二者形成一种串联而又相对独立的关系，最后再组合成伺服进给模型.
1.1 伺服控制系统建模
在数控机床进给控制中，大多采用永磁同步电机.永磁同步伺服控制系统由伺服电机和伺服驱动器组成，伺服电机的主体是永磁同步电机，伺服驱动器由脉宽调制(PWM)三相逆变器和电流环、速度环(内环)、位置环(外环)多环控制系统组成[2].
伺服系统位置环可保证系统静态精度和动态跟踪性能，使整个伺服系统稳定高效运行.位置调节器采用模糊PID控制器，电流环和速度环均采用PI调节器[3]，可使数控伺服系统无超调、快速地控制位置.伺服控制系统图如图1所示.
1.2 机械进给传动系统建模
常见的数控机床进给传动系统结构[4]如图2所示，其中，J1、k1、Tm、θm分别为电机轴的转动惯量、扭转刚度、输出转矩和输出转角；J2、k2分别为滚珠丝杠的转动惯量和扭转刚度；m、c、k3、x(t)分别为工作台的质量、工作台与导轨和滚珠丝杠之间的移动阻尼系数、滚珠丝杠副的拉压刚度和工作台的位移；F为切削力、摩擦力及干扰等.
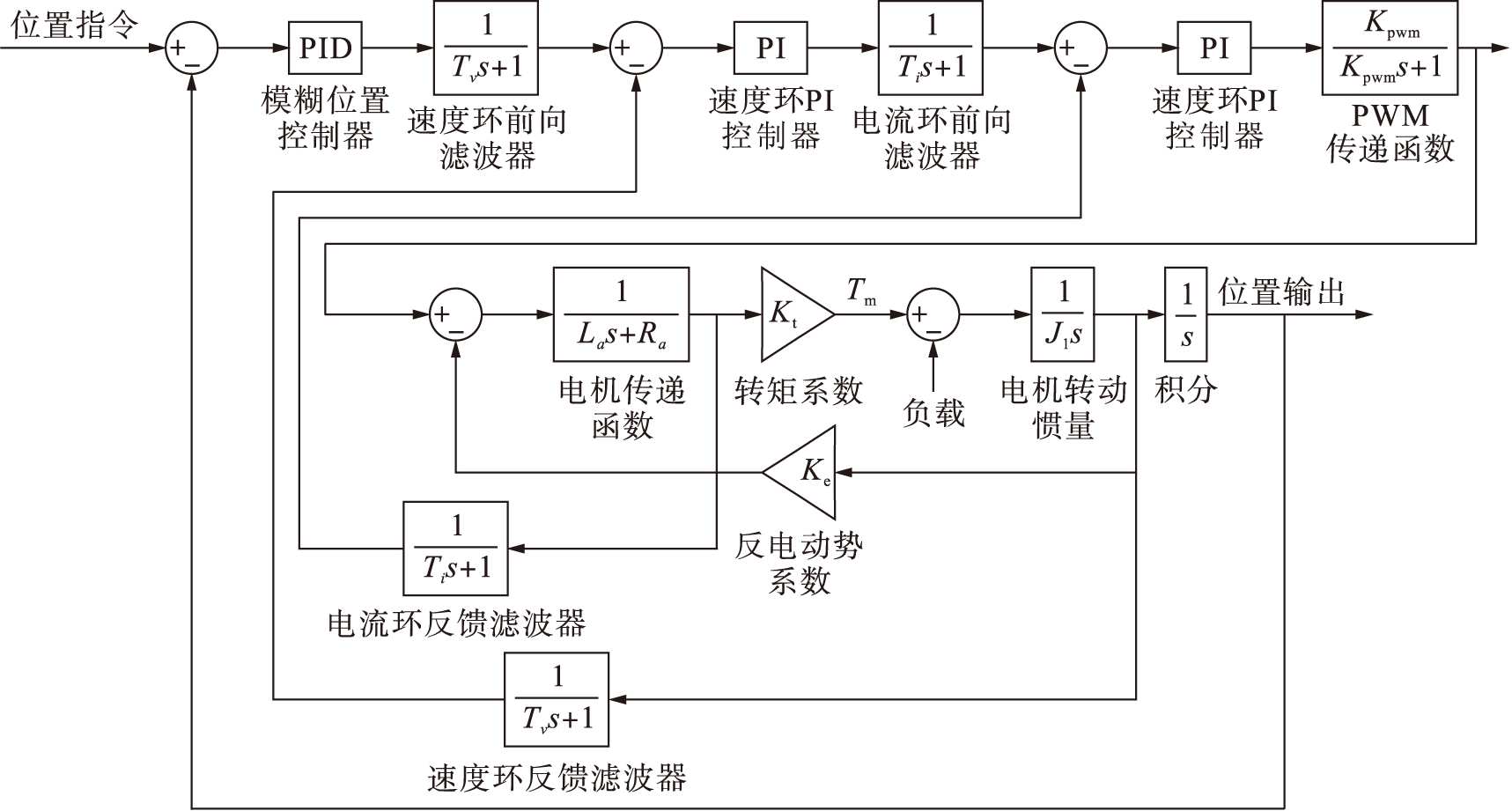
图1 伺服控制系统图
Fig.1 Servo control system diagram
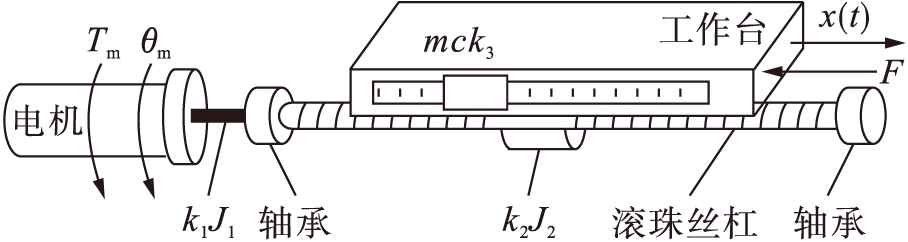
图2 机械进给机构
Fig.2 Mechanical feed mechanism
将系统向电机轴转化，根据等效原理得到系统的动力学方程为
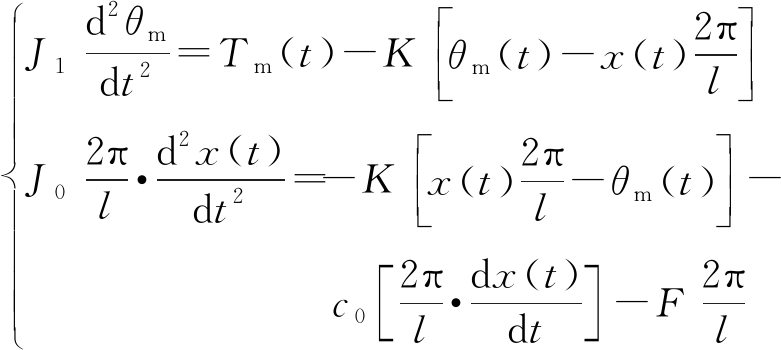
(1)
式中：K为系统等效扭转刚度，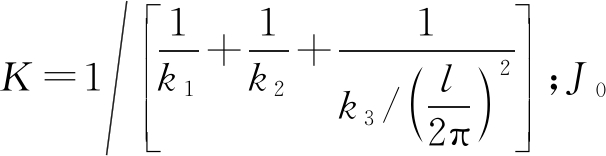
为工作台与滚珠丝杠向滚珠丝杠转化的等效转动惯量，
为等效转动阻尼系数，
为滚珠丝杠导程，导程系数
对式(1)进行拉普拉斯变换，得到进给伺服系统机械部分的系统框图如图3所示.
以θ为输入，x为输出时，机械传动系统是一个二阶振荡环节，其传递函数为
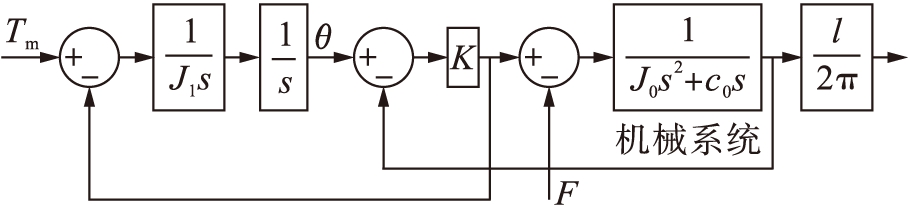
图3 机械进给系统图
Fig.3 Mechanical feed system diagram
(2)
式中：
为机械系统的固有频率；
为机械系统的相对阻尼比.
2 数控进给伺服系统的模糊PID控制
2.1 模糊PID控制器设计
进给伺服系统的模糊PID控制器结构如图4所示，由PID控制器和模糊参数调节器两部分组成.控制器可根据系统误差大小，自适应地调节PID控制器的3个参数，从而实现参数整定的智能化.
图4 模糊PID控制器结构
Fig.4 Fuzzy-PID controller structure
2.2 基于遗传算法的模糊控制器设计
基于遗传算法(GA)的模糊控制器结构如图5所示.将模糊控制器的模糊规则编码成遗传算法的染色体，用GA在线优化控制规则，使模糊控制器具有自学习功能.这种控制算法结合了GA和模糊控制各自的优点，且不依赖于精确的系统模型[5].
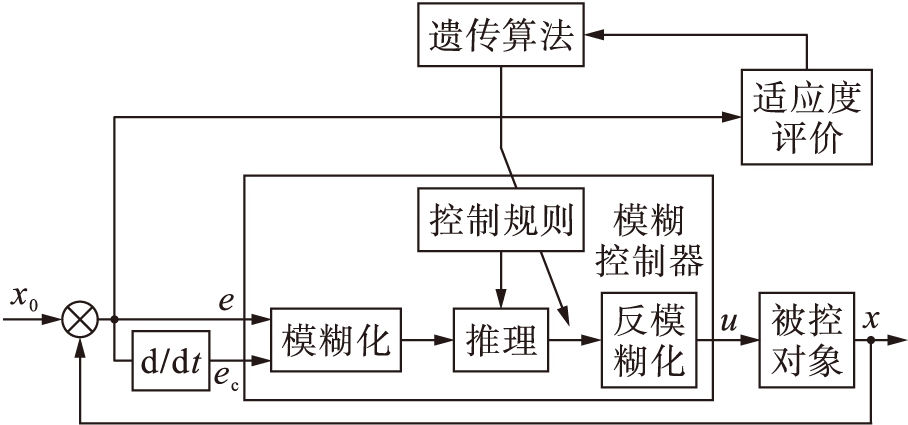
图5 基于GA的模糊控制器结构
Fig.5 Fuzzy controller structure based on GA
2.3 伺服系统仿真
本文以数控高速铣齿机床Z向进给的位置伺服系统为研究对象，电机型号为1FK6102，其参数[6]见表1.
表1 电机参数
Tab.1 Parameters for motor
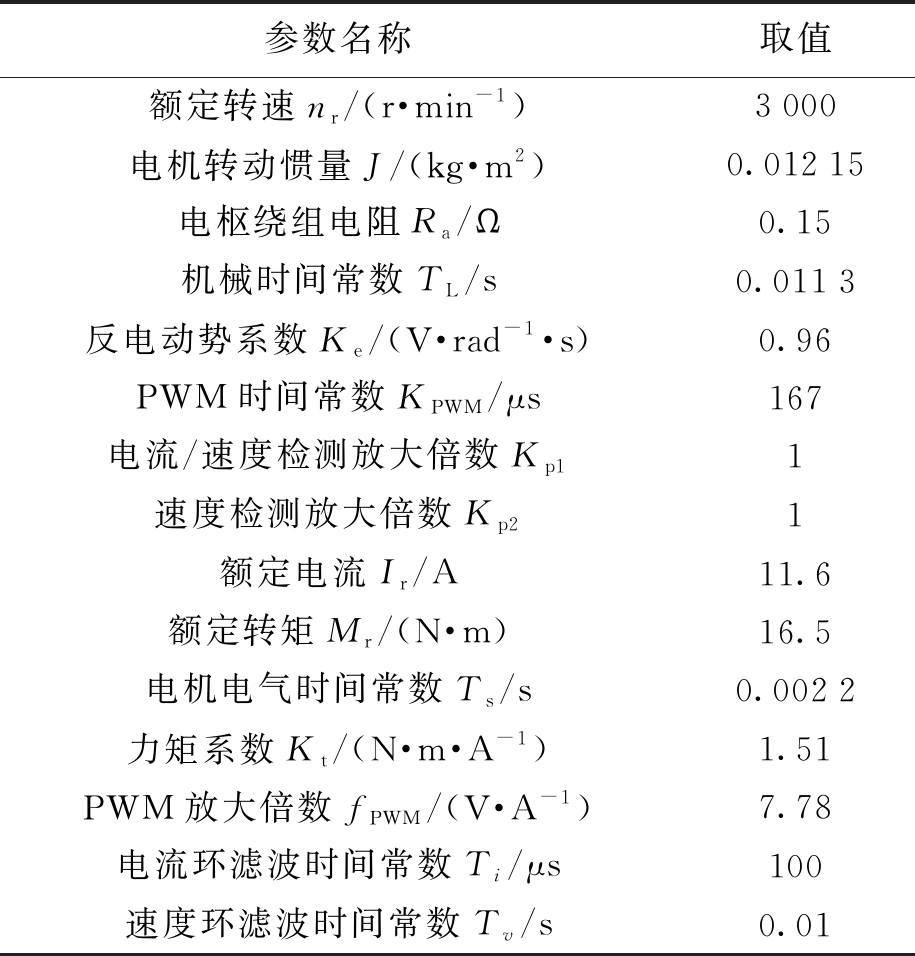
参数名称取值额定转速nr/(r·min-1)3000电机转动惯量J/(kg·m2)0.01215电枢绕组电阻Ra/Ω0.15机械时间常数TL/s0.0113反电动势系数Ke/(V·rad-1·s)0.96PWM时间常数KPWM/μs167电流/速度检测放大倍数Kp11速度检测放大倍数Kp21额定电流Ir/A11.6额定转矩Mr/(N·m)16.5电机电气时间常数Ts/s0.0022力矩系数Kt/(N·m·A-1)1.51PWM放大倍数fPWM/(V·A-1)7.78电流环滤波时间常数Ti/μs100速度环滤波时间常数Tv/s0.01
建立如图6所示的进给伺服系统仿真模型，其中PIDsimf函数实现了PID控制.函数PIDsimf共有5个输入参数，分别为时间t，误差e，参数kp，ki，kd(对应于u1，u2，u3，u4，u5).
将采样周期T设定为1 ms，在系统位置控制中分别使用常规PID和模糊PID控制器(F-PID)，并进行对比分析.PID控制器调节时间为0.6 s，F-PID控制器调节时间为0.25 s.F-PID控制器比常规PID控制器调节时间短、动态响应性能和跟踪性能好，抗干扰能力强.
3 数控进给伺服系统的摩擦补偿
3.1 摩擦建模
为克服摩擦进给伺服系统带来的危害，提高伺服系统的性能，建立一个加入Stribeck速度的Stribeck摩擦模型，其表达式[7]为
F=Fcsgn(v)+bv+(Fs-Fc)-(v/vstr)δs
(3)
式中：F为摩擦力；Fc为库仑摩擦力；Fs为滑动摩擦力；b为黏滞摩擦系数；vstr为Stribeck速度；δs为经验参数，本文取2，它和vstr一起决定部分液体润滑时摩擦曲线的形状.Stribeck模型是非线性模型，取决于伺服系统的瞬时速度值，更符合实际摩擦，既能体现Stribeck现象，又能体现静摩擦力作用.本文选取Stribeck+静摩擦力模型，其表达式为
当v=0 m/s时，
(4)
式中，Fe为摩擦力输出值.
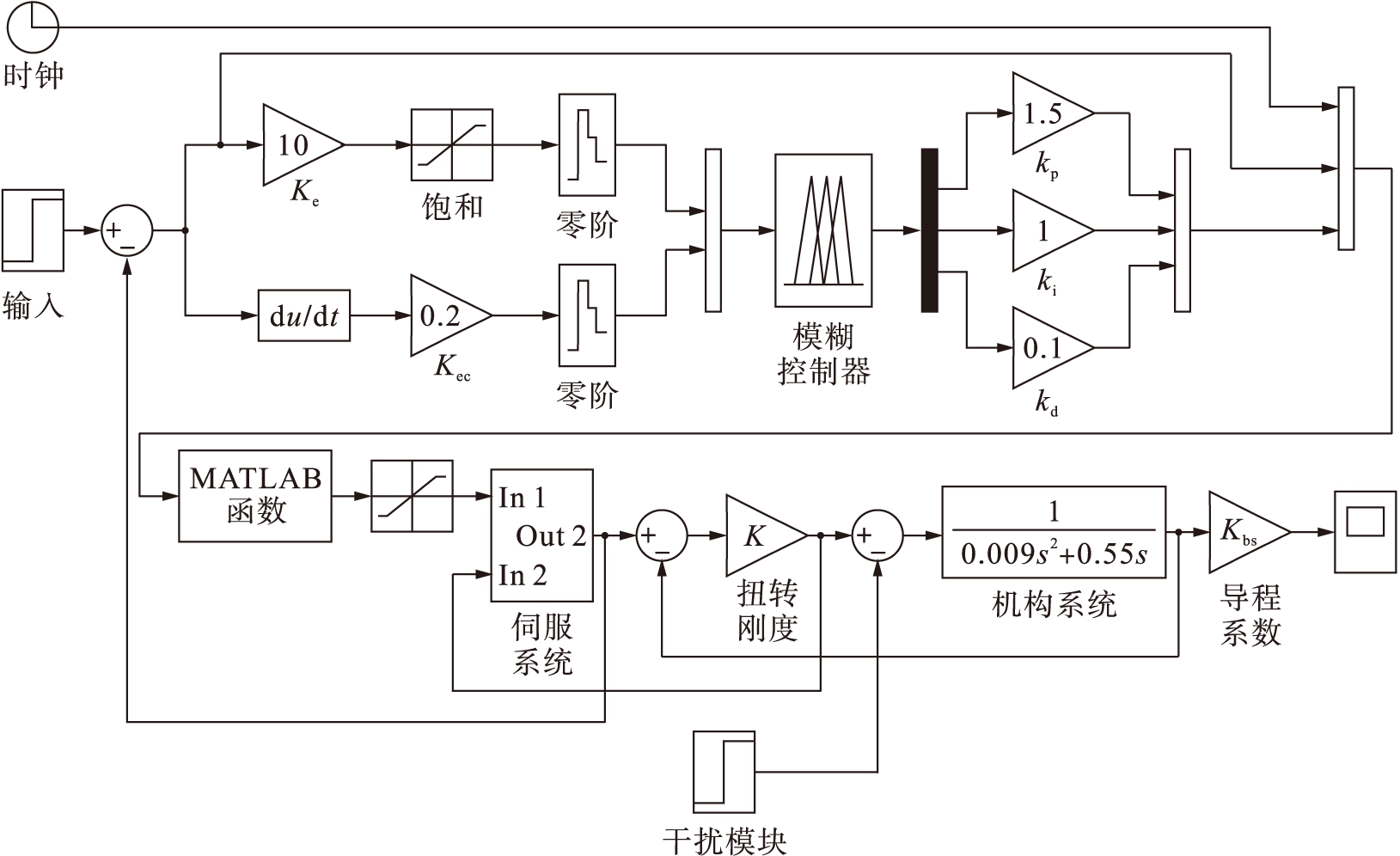
图6 进给伺服数控系统仿真模型
Fig.6 Simulation model for feed servo NC system
当v≠0 m/s时，计算表达式同式(3).
3.2 摩擦补偿仿真
3.2.1 摩擦仿真模型建立
处于静摩擦力阶段时速度为零，而此阶段的摩擦力随外力的变化而变化.为了表达此阶段的静摩擦力现象，将前馈通道加入摩擦仿真模型中，摩擦力输出值为Fe，此时系统的合力为零[8]，这一作用在Simulink中通过逻辑运算模块实现.设-v0<v<+v0时，v=0 m/s，取v0=1×10-5 m/s.摩擦仿真模型如图7所示.
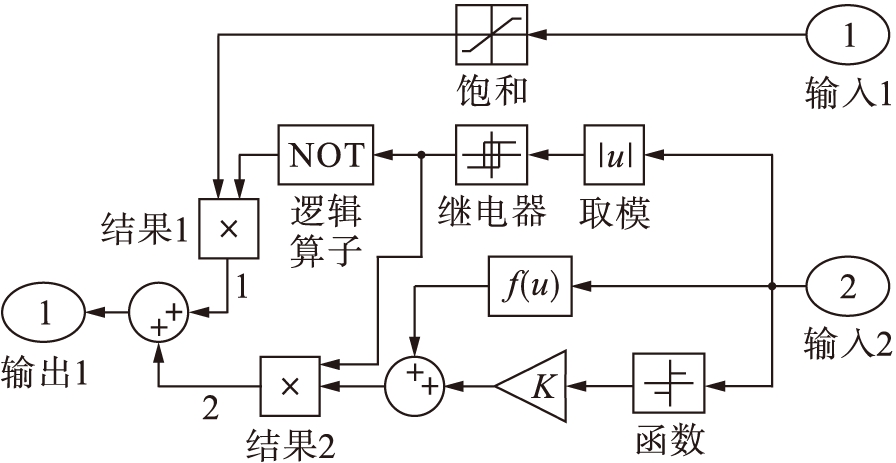
图7 摩擦仿真模型
Fig.7 Friction simulation model
图7中，输入1、2分别为Fe和v，当|v|<v0时，通道1接通，摩擦力输出值为Fe，v=0 m/s时的摩擦力等于外力；|v|≥v0时，通道2接通，输出为Stribeck摩擦力.摩擦模型的仿真参数为：最大静摩擦力Fs=2.6 N，库仑摩擦力Fc=1.8 N，黏滞摩擦系数b=5.7，Stribeck临界速度vstr=0.001 m/s.
3.2.2 仿真分析
将单纯的PID控制器和模糊PID控制器(F-PID)分别应用于位置控制中，并设定采样周期T为1 ms.当输入信号为单位阶跃信号时，则阶跃响应曲线如图8所示.
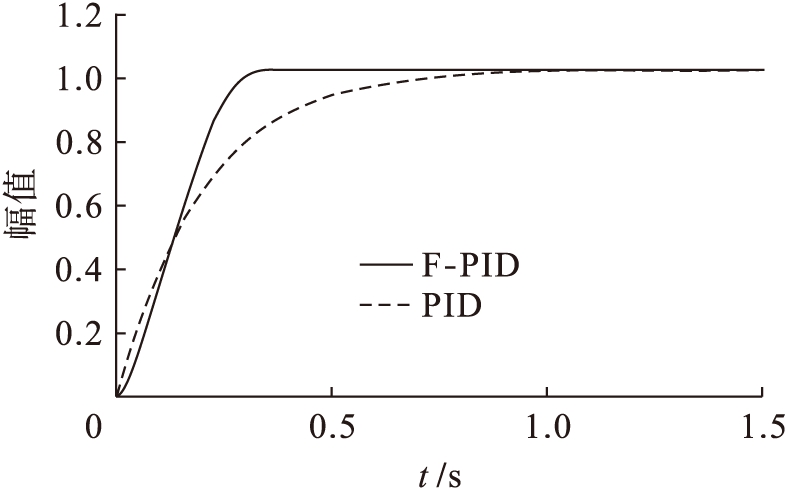
图8 单位阶跃响应
Fig.8 Unit step response
在阶跃输入条件下，1 s时刻加入0.2倍阶跃干扰，获得的响应曲线如图9所示.
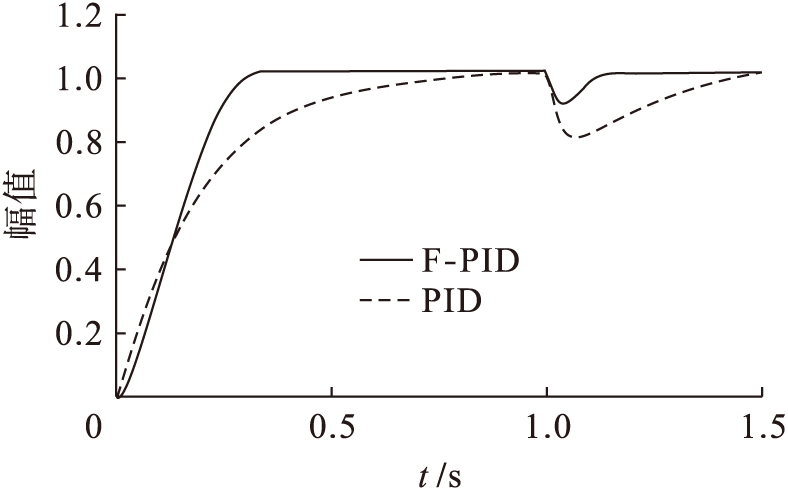
图9 干扰响应
Fig.9 Disturbance response
从图9可以看出，PID控制器的调节时间为0.6 s，F-PID控制器的调节时间为0.25 s，F-PID控制策略响应速度更快，调节时间更短，具有良好的动态性能.采用F-PID控制策略时，系统很快将干扰减小，并在较短的时间内跟踪了给定信号.因此，当系统采用F-PID控制策略时，能够获得更好的响应性能和跟踪性能，并且具有更强的鲁棒性和抗干扰能力.
4 结 论
在伺服控制和机械进给综合模型的基础上，采用模糊PID和遗传算法优化模糊规则策略，对数控进给伺服系统的整体性能进行仿真研究.仿真结果表明，模糊PID控制器比常规PID控制器抗干扰能力强，跟踪误差小，数控伺服系统的低速爬行现象得到有效抑制.实际应用中，需进行试验比较来确定合适的算法初始值，以达到预期的补偿效果.
[1]郑子文.超精密机床伺服控制技术研究 [D].长沙：国防科学技术大学，2002.
(ZHENG Zi-wen.Study on servo control technology of ultra-precision machine tool [D].Changsha：University of National Defense Science and Technology，2002.)
[2]白传栋，王德义.交流位置伺服系统非线性摩擦补偿控制研究 [J].太原理工大学学报，2015，46(4)：430-434.
(BAI Chuan-dong，WANG De-yi.Study on nonlinear friction compensation control of ac position servo system [J].Journal of Taiyuan University of Technology，2015，46(4)：430-434.)
[3]王丽梅，武琳，刘春芳.永磁直线同步电动机自适应摩擦补偿控制 [J].沈阳工业大学学报，2009，31(3)：252-256.
(WANG Li-mei，WU Lin，LIU Chun-fang.Adaptive friction compensation control for permanentmagnet linear synchronous motor [J].Journal of Shenyang University of Technology，2009，31(3)：252-256.)
[4]孙宜标，王亚朋，刘春芳.永磁直线电机自适应区间二型模糊滑模控制 [J].沈阳工业大学学报，2017，39(6)：601-606.
(SUN Yi-biao，WANG Ya-peng，LIU Chun-fang.Adaptive interval type-2 fuzzy sliding mode control for permanent magnet linear motor [J].Journal of Shen-yang University of Technology，2017，39(6)：601-606.)
[5]韩秋奎，张金宝.基于 RLS 的 KV800 数控机床伺服控制系统设计与研究 [J].制造技术与机床，2017(5)：62-66.
(HAN Qiu-kui，ZHANG Jin-bao.Design and research of servo control system of KV800 CNC machine tool based on RLS [J].Manufacturing Technology & Machine Tool，2017(5)：62-66.)
[6]王勇，郑昊.基于模糊 PID 的数控折弯机比例伺服控制系统 [J].锻压技术，2016，41(11)：98-103.
(WANG Yong，ZHENG Hao.Proportional servo control system of CNC bending machine based on fuzzy PID [J].Forging and Stamping Technology，2016，41(11)：98-103.)
[7]沙丰永，高军，李学伟，等.数控机床多惯量伺服系统控制仿真研究 [J].计算机仿真，2016，33(8)：197-200.
(SHA Feng-yong，GAO Jun，LI Xue-wei，et al.Research on simulation of CNC multi-inertia servo control system of machine tools [J].Computer Simulation，2016，33(8)：197-200.)
[8]史晓娟，杨紫艳.基于模糊滑模控制的数控机床位置伺服系统 [J].制造技术与机床，2017(3)：64-68.
(SHI Xiao-juan，YANG Zi-yan.CNC machine tool position servo system based on fuzzy sliding mode control [J].Manufacturing Technology & Machine Tool，2017(3)：64-68.)