混沌，作为非线性现象，广泛存在于各个研究领域，如医学、化学、生物学和经济学等，其研究方式也从最初的消除混沌变为研究混沌[1]和应用混沌[2]，通常先通过计算机软件调试出混沌系统，再将其应用到用电预测[3]、图像加密和安全通信[4]等领域.在这样的背景下，许多特殊的混沌系统[5]不断被提出，如变换参数会呈现不同类型平衡点的多特征混沌系统、分数阶导数的混沌系统[6]、具有无穷多平衡点或者没有平衡点的混沌系统[7]、轮胎形和喇叭形的混沌系统、切换混沌系统[8]、平移混沌系统等.很多学者也致力于混沌同步的研究，目前，在许多系统上，不仅实现了两个或三个系统之间的自适应同步[9]、反同步、广义同步、投影同步、混合同步[10]，而且完成了不同维数系统间的同步.其中，在自适应同步中，自适应同步器能够不断读取驱动系统的信息，使得响应系统能够逐渐调整，最终与驱动系统同步.本文提出的带有立方项的分段切换混沌系统，由一个混沌系统和一个非混沌系统切换生成，该切换混沌系统呈锥形，在x1-x2平面上的投影为苹果形.
1 带立方项混沌系统
1.1 混沌系统概述
本文提出一种新的带立方项的混沌系统，其由两个系统切换产生.第1个系统的表达式为
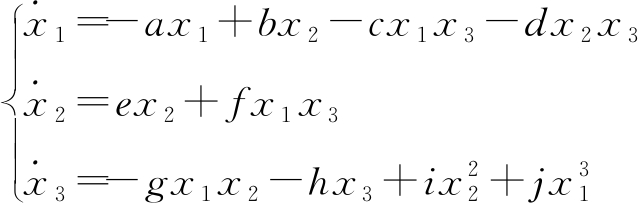
(1)
式中，a、b、c、d、e、f、g、h、i、j为系统中的未知参数.每个参数都在一定的范围内使得系统是混沌的，并且系统的相图在参数不同时，往往也有较大的变化.系统(1)中一共有10项，其中，二次交叉项、平方项、立方项和线性项的个数分别为4、1、1、4个.
1.2 混沌系统的相图及Lyapunov指数谱
通过计算机仿真，当a=15，b=12，c=1，d=2，e=10，f=8，g=7，h=9，i=2.8，j=0.5时，系统呈混沌态，如图1所示.
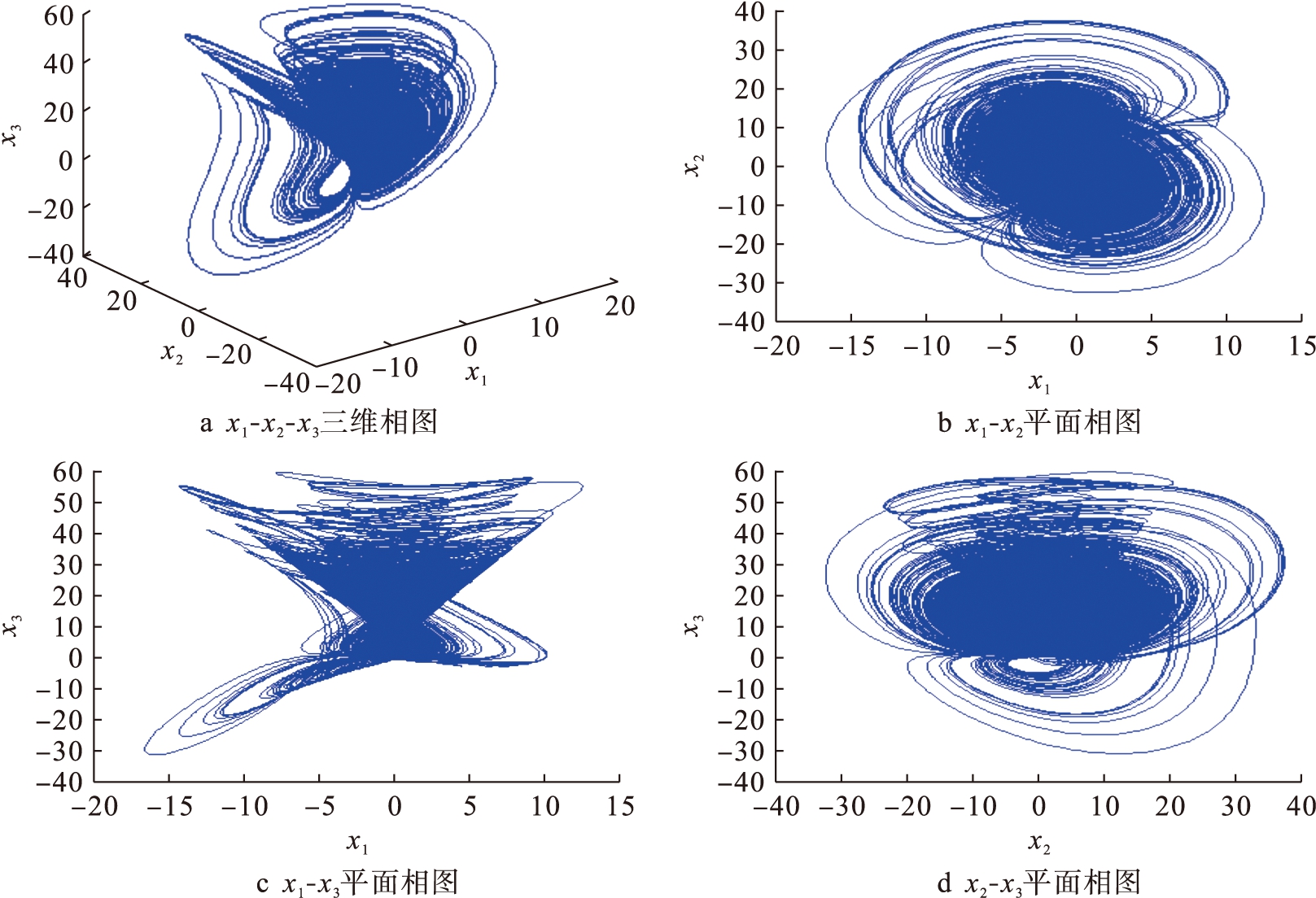
图1 系统(1)的相图
Fig.1 Phase diagram of system(1)
Lyapunov指数谱是一种定量分析的方法，系统(1)的Lyapunov指数谱如图2所示.
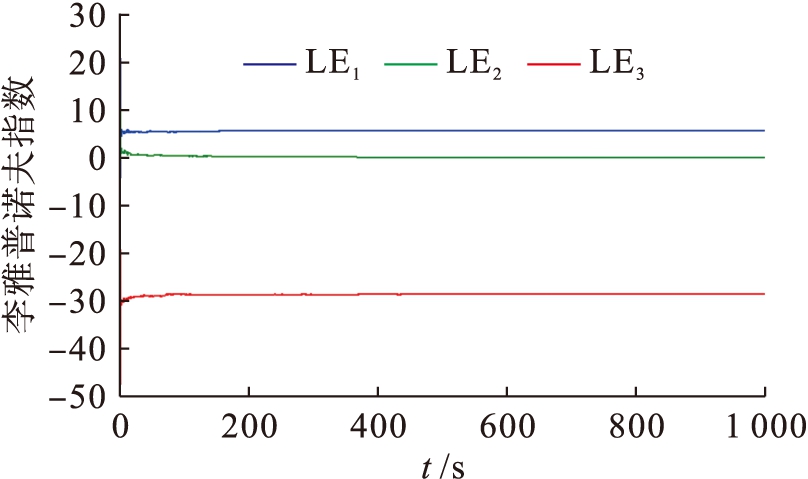
图2 系统(1)的Lyapunov指数谱
Fig.2 Lyapunov exponent spectrum of system(1)
LE1、LE2、LE3为随时间t变化的李雅普诺夫指数，LE1>0，LE2=0，LE3<0，LE1+LE2+LE3<0，系统混沌.
2 加入线性项的非混沌系统
第2个系统的表达式为
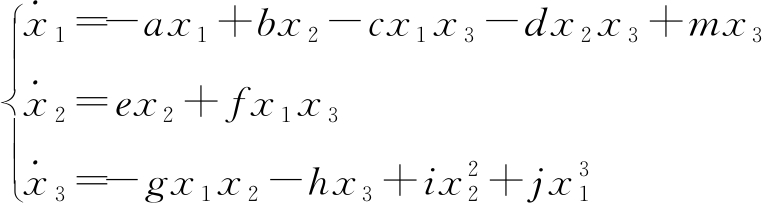
(2)
式中，a、b、c、d、e、f、g、h、i、j、m为与系统(1)相同的未知参数.系统(2)比系统(1)多一项，共11项，其中，非线性项和线性项的个数分别为6、5个，当a=15，b=12，c=1，d=2，e=10，f=8，g=7，h=9，i=2.8，j=0.5，m=6时，相图如图3所示.
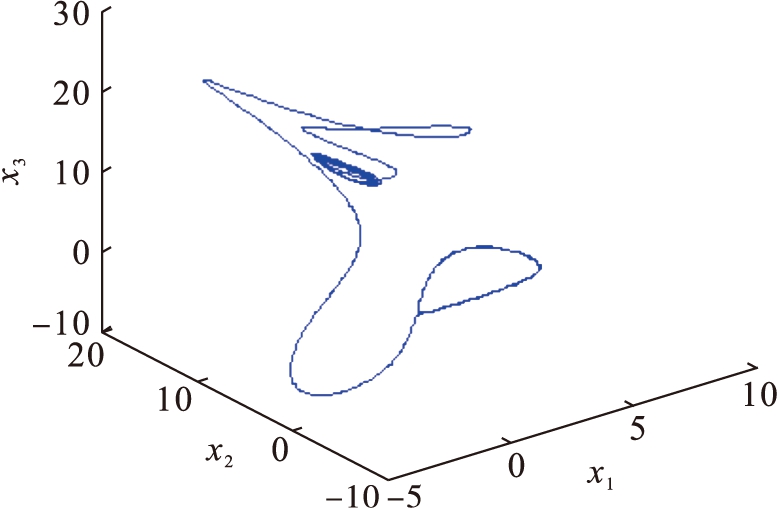
图3 系统(2)的三维空间相图
Fig.3 3D spatial phase diagram of system(2)
系统(2)的Lyapunov指数谱如图4所示.由图4可知，系统(2)是非混沌的.
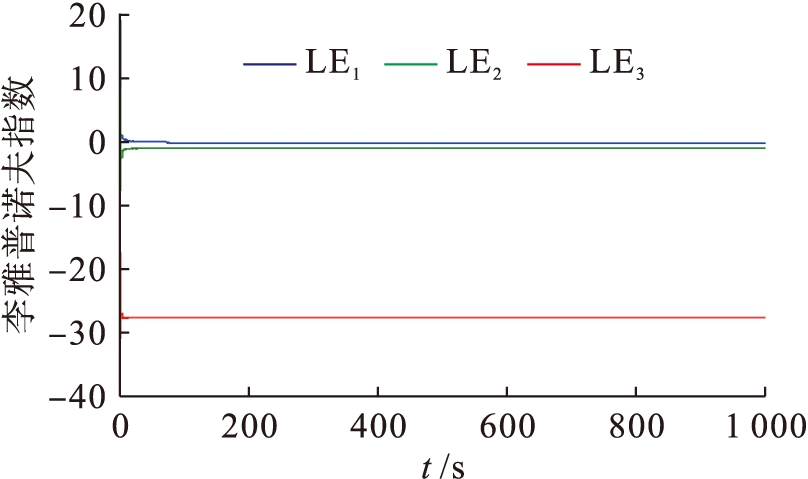
图4 系统(2)的Lyapunov指数谱
Fig.4 Lyapunov exponent spectrum of system(2)
3 带立方项切换混沌系统
3.1 切换混沌系统概述
当x2>0时，运行系统(1)，当x2≤0时，运行系统(2)，得到带立方项的切换混沌系统，其表达式为
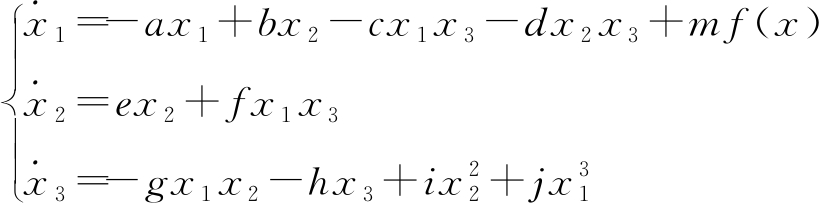
(3)
式中，
3.2 切换混沌系统的相图及庞加莱映射图
当a=15，b=12，c=1，d=2，e=10，f=8，g=7，h=9，i=2.8，j=0.5，m=6时，系统(3)的相图如图5所示.系统(3)的相图形状经过折叠和旋转，最后大致呈锥面，且在x1-x2面上的投影为苹果形状.
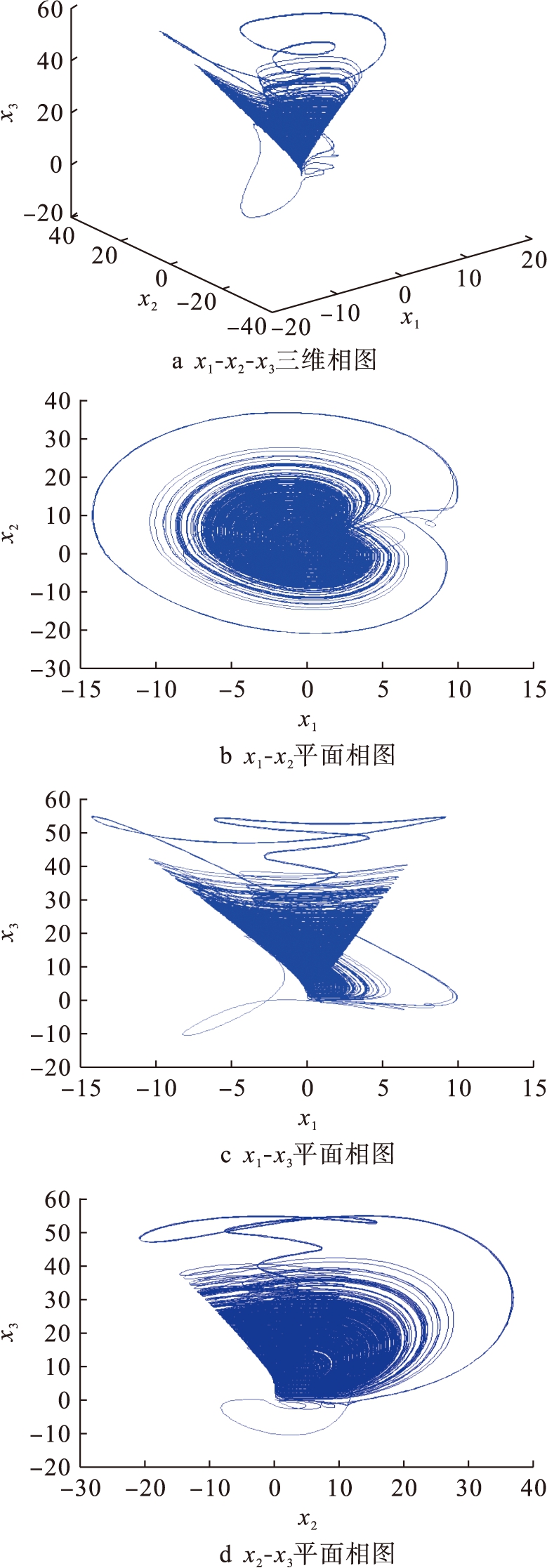
图5 系统(3)的相图
Fig.5 Phase diagram of system(3)
本文采用庞加莱截面法讨论动力系统(3)的性态，图6为在x3=32截面上，用计算机模拟出的庞加莱映射，图中呈现出成片密集的点，且富有层次性，进一步说明该系统的吸引子具有复杂的折叠行为.
3.3 切换混沌系统平衡点
系统(3)的雅克比矩阵为
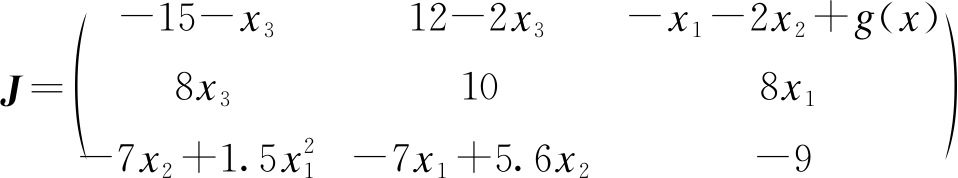
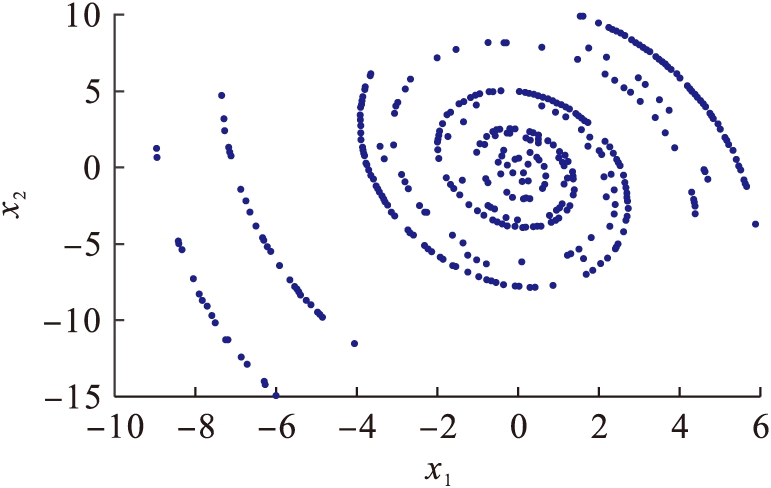
图6 x3=32截面上的庞加莱映射
Fig.6 Poincare mapping on cross section with x3=32
其中，
令
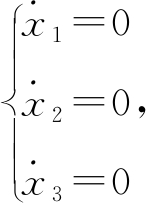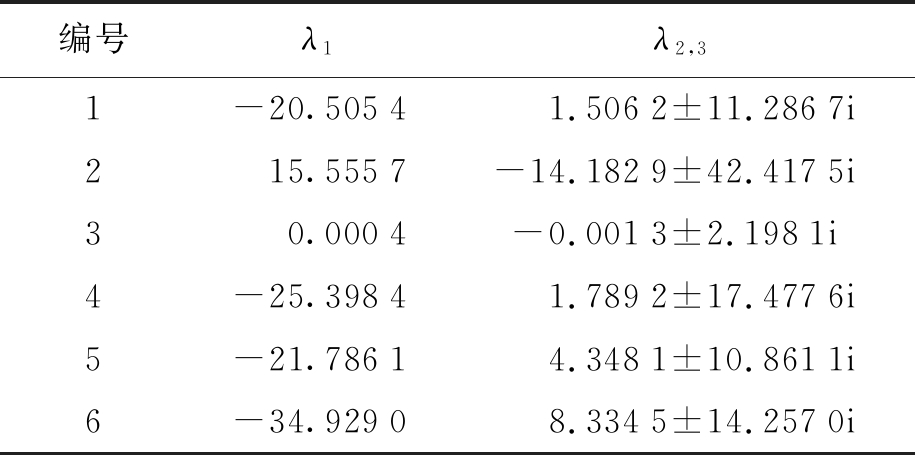
可得系统(3)的平衡点S1=(1.83，1.75，-1.19)，S2=(7.93，7.60，-1.19)，S3=(-306.98，1 921.27，7.82)，S4=(-0.68，4.24，7.82)，S5=(-1.38，-1.01，-0.91)，S6=(0.82，-2.8，4.26)，再由|JE-λ|Si=0，可得系统(3)的特征值如表1所示.
表1 系统(3)的特征值
Tab.1 Eigenvalues of system(3)
编号λ1λ2,31-20.5054 1.5062±11.2867i215.5557-14.1829±42.4175i30.0004-0.0013±2.1981i4-25.39841.7892±17.4776i5-21.78614.3481±10.8611i6-34.92908.3345±14.2570i
因此，系统(3)的诸多平衡点均为不稳定的鞍焦点，具备产生涡卷的条件.
4 自适应控制器的设计与仿真实验
4.1 自适应控制器的设计
本文令系统(3)为驱动系统，系统(4)为响应系统，其中，u1、u2、u3为控制器，则有
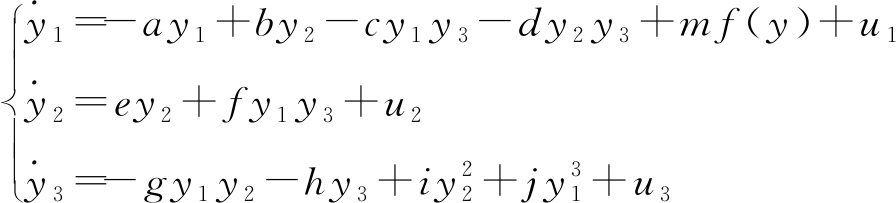
(4)
令e1=y1-x1，e2=y2-x2，e3=y3-x3，由式(4)减去式(3)可得
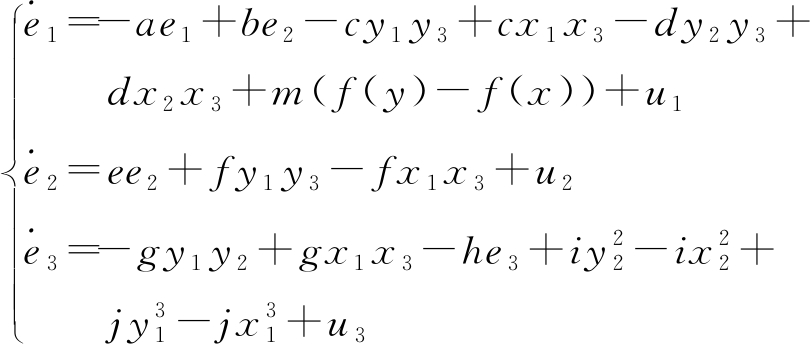
(5)
令
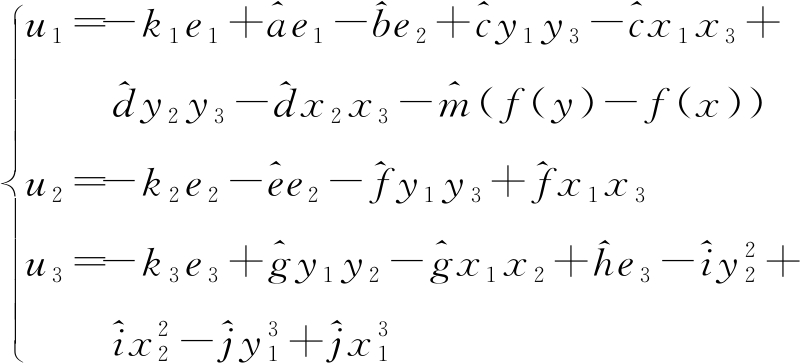
(6)
将式(6)代入式(5)，则有
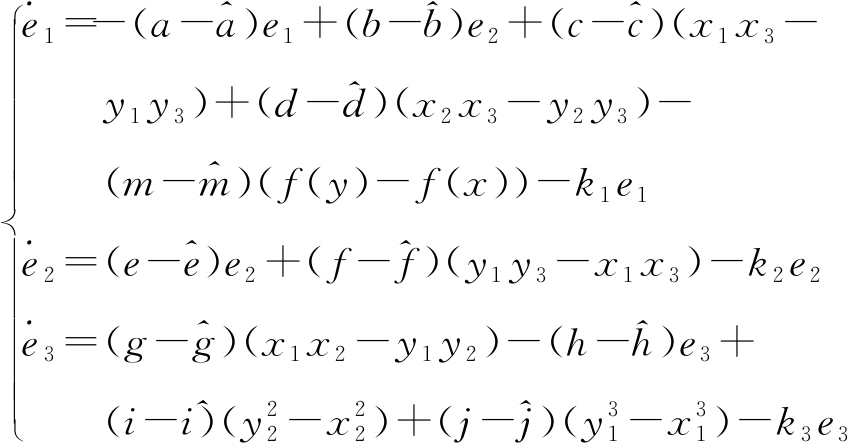
(7)
令
式(7)可转换为
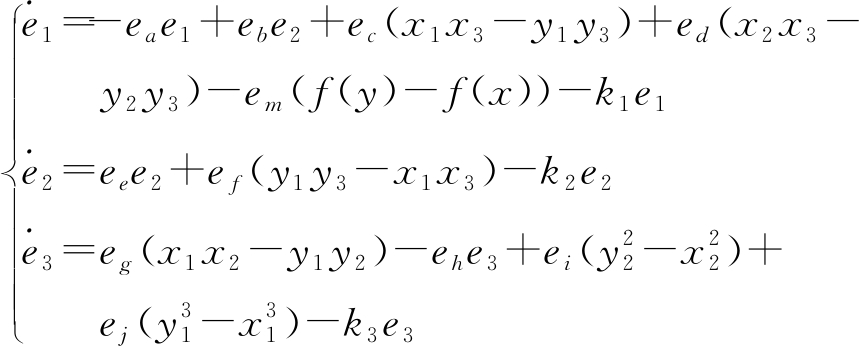
(8)
由此可知，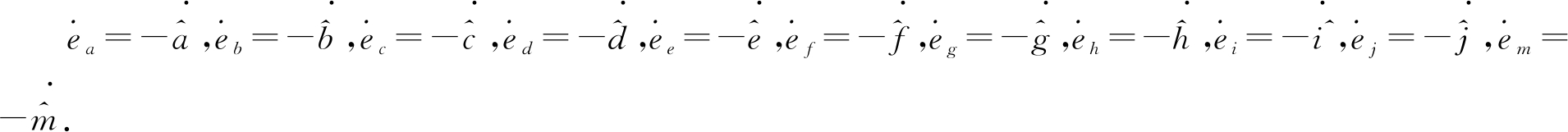
取Lyapunov函数为
该函数在R6上是正定函数，即
=e1[-eae1+ebe2+ec(x1x3-y1y3)+ed(x2x3-
y2y3)-em(f(y)-f(x))-k1e1]+e2[eee2+
ef(y1y3-x1x3)-k2e2]+e3[eg(x1x2-y1y2)-
=
取更新规则为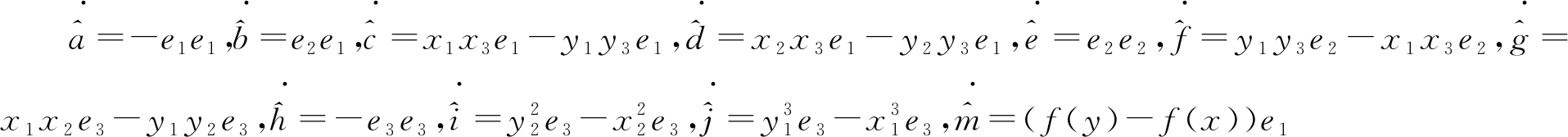
时，
根据Lyapunov函数稳定性定理，经一段时间后，系统(3)、(4)随时间t的运动轨线将一致.
4.2 仿真实验
图7为计算机模拟出的误差曲线随时间t的变化轨线，可以看出，在很短的时间内，误差即稳定为0.
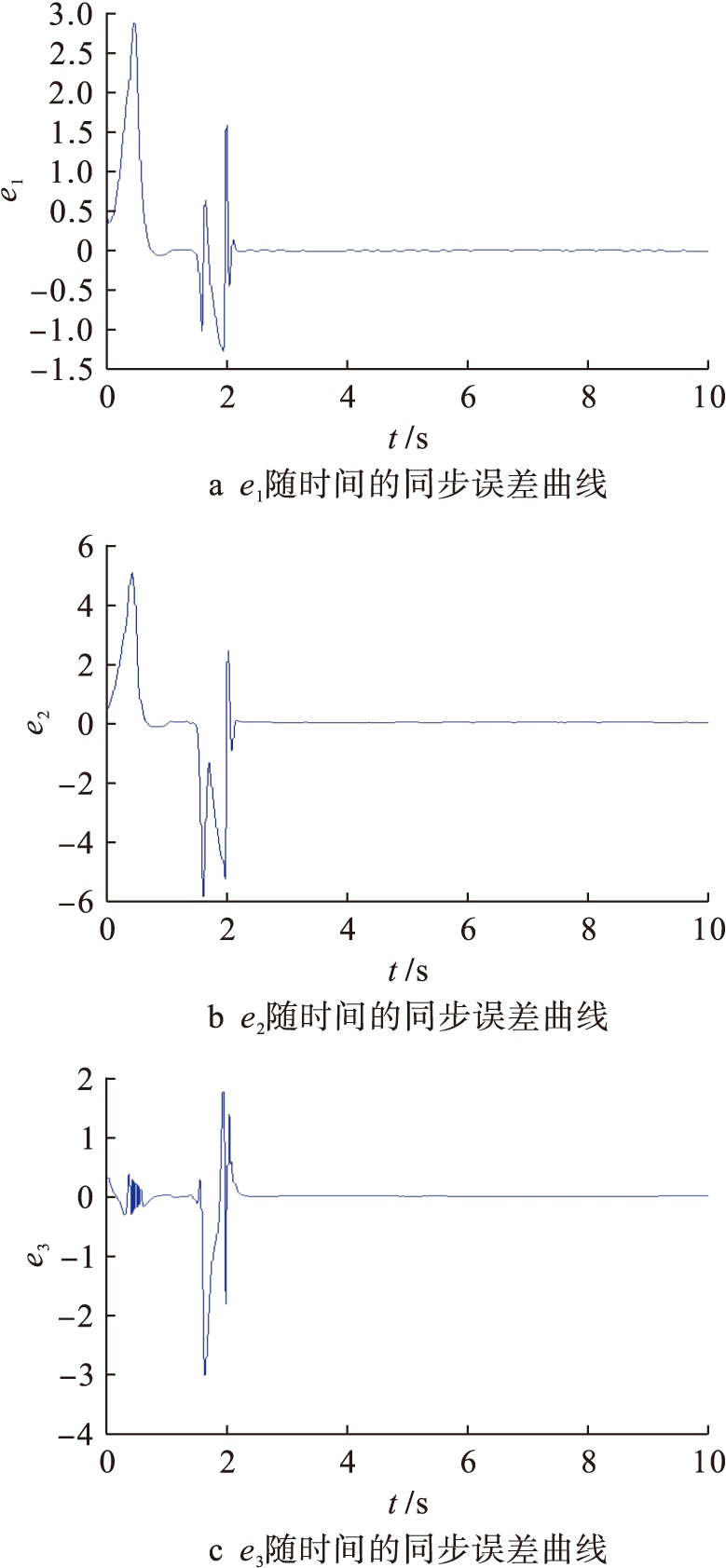
图7 加入控制器时系统(3)、(4)的同步误差曲线
Fig.7 Synchronization error curves of systems (3) and (4) with action of controllers
5 结 论
本文在提出的带三次项三维混沌系统中加入了简单的线性切换项后，其吸引子的图像更为特殊和新颖.采用的自适应控制器及更新规则设计方案，对具有高次项和切换项的混沌系统均适用，且在易于实现的基础上，同步速度也非常快.
[1]赵柏山，刘晓晓，张学松.一种限定混沌状态变量运动区域的方法 [J].沈阳工业大学学报，2019，41(1)：62-67.
(ZHAO Bo-shan，LIU Xiao-xiao，ZHANG Xue-song.A method of limiting motion area of chaotic state varia-bles [J].Journal of Shenyang University of Techno-logy，2019，41(1)：62-67.)
[2]Han C Y，Yu S M.Generating chaos via nonlinear system switching anti-control and circuit implementation [J].International Journal for Light and Electron Optics，2014，125(14)：3491-3498.
[3]李媛，武岩岩，王思琪.基于混沌时间序列的Elman神经网络工业用电预测 [J].沈阳工业大学学报，2016，38(2)：196-199.
(LI Yuan，WU Yan-yan，WANG Si-qi.Elman neural network for forecasting industrial electricity consumption based on chaotic time series [J].Journal of Shenyang University of Technology，2016，38(2)：196-199.)
[4]Israr A，Muhammad S，Mossa A S.Globally exponential multi switching-combination synchronization control of chaotic systems for secure communications [J].Chinese Journal of Physics，2018，56(3)：974-987.
[5]Wu J N，Wang L D，Chen G R，et al.A memristive chaotic system with heart-shaped attractors and its implementation [J].Chaos，Solitons and Fractals，2016，92：20-29.
[6]Zambrano S E，Mu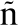
oz P E，Campos C.Chaos generation in fractional-order switched systems and its digital implementation [J].International Journal of Electro-nics and Communications，2017，79：43-52.
[7]Viet T P，Sajad J，Christos V，et al.A gallery of chao-tic systems with an infinite number of equilibrium points [J].Chaos，Solitons and Fractals，2016，93：58-63.
[8]Ayub K，Mridula B，Aysha I.Multi-switching dual compound synchronization of chaotic systems [J].Chinese Journal of Physics，2018，56(1)：171-179.
[9]Viet T P，Sundarapandian V，Christos V，et al.A no-equilibrium hyperchaotic system with a cubic nonlinear term [J].International Journal for Light and Electron Optics，2016，127(6)：3259-3265.
[10]Viet T P，Adel O，Christos V，et al.A simple fractional-order chaotic system without equilibrium and its synchronization [J].International Journal of Electro-nics and Communications，2018，86：69-76.