随着我国经济的高速发展，电力系统网络的规模不断扩大，结构也日益复杂，因此对电力系统运行的稳定性和可靠性提出了更高的要求.通常情况下认为电力系统中的发电、输电、配电等环节在运行时都应处于三相对称状态，但事实上，随着发电容量的增大，输电电压等级的升高，以及用电负荷多样化，电力系统在实际运行中很难达到严格对称的理想状态[1].
输电线路参数不对称这一现象在目前的高压输电线路中是比较常见的，主要是由于在高压输电网中，为保证线路的机械及电气强度，往往不再对线路进行换位处理[2]，同塔双回甚至多回线路中复杂的电磁耦合[3-4]以及在线路架设施工和运行中的各种因素，都会使输电线路三相参数间存在差异，无法满足对称的条件.不对称线路参数会在线路上产生很大的不对称电压及电流，这不仅会在电能传输过程中产生更大的损耗，而且可能会影响线路两端电气设备的正常运行[5]，因此在电能质量国家标准GB/T15543-2008中规定，电网在正常运行时负序电压不平衡度不得超过2%，短时不得超过4%[6].目前对于线路参数不对称问题的研究，主要集中在同塔双回或多回线路中相序的排列方式上，文献[7-9]针对不同类型及电压等级的输电线路提出了不同的线路相序排列方式，可以有效降低线路上的不平衡电压及电流.这对于还未建成的输电线路具有一定的指导意义，但对于已经建成并投入运行的线路来说，若三相导线采用垂直排列的方式架设还有可能改变其相序排列方式，若是采用水平或三角形排列的方式架设，则不可再改变它的相序排列方式，并且改变运行线路的排列方式既不安全也不经济.文献[10]探讨了通过在线路中合理接入无源元件以修改线路互感矩阵参数来减小负序电流分量的可行性，但未考虑三相线路自阻抗不等对于线路不平衡度的影响.
本文提出将首端电源的三相输电线路看作一个含源多口网络的线路模型，根据广义诺顿定理写出模型的诺顿等值电路，通过调节线路末端变电站中静止无功补偿设备的投切量，使其端口电压接近三相对称，从而达到降低线路上不对称电压的效果.
1 广义诺顿定理
根据含源多口网络不同描述方式，可以得到不同的等值电路.对于端口施加电压源激励的含源网络，如果该网络具有唯一解，则该含源多口网络可表示为
I=YscU+Isc
(1)
式中：Ysc为短路导纳矩阵；Isc为短路导纳电流.图1为广义诺顿电路图，图1b方框内为非含源多口网络，每一端口并联一个电流源I1sc、I2sc、、Imsc.可见，一个含源多口网络N可用一个每一端口并联电流源的非含源多口网络N0等效替代.这一结论是含源单口网络诺顿定理的推广，故称为广义诺顿定理[11].
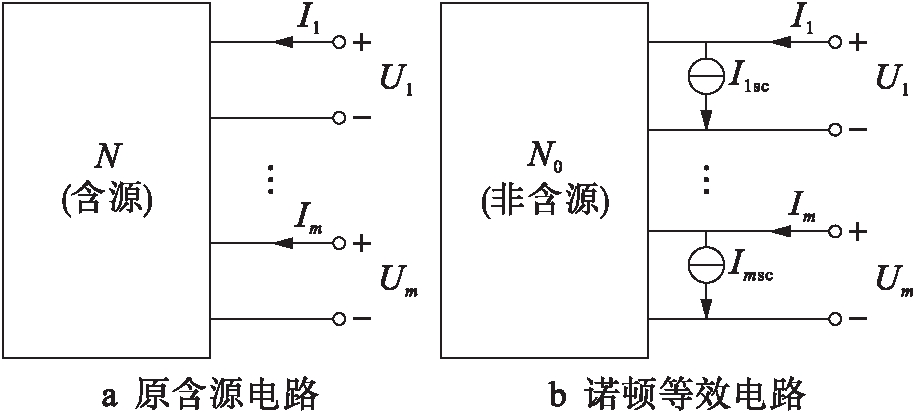
图1 广义诺顿电路图
Fig.1 Generalized Norton circuit diagram
对于诺顿等值电路中的短路导纳矩阵Ysc中的元素，其列写准则为当每个电压源单独作用时其余端口均短路，每一端口电流与该电压源电压的比值，即
(2)
当j=k时，可得
(3)
式(2)、(3)表明，Ykk是其余端口短路情况下第k个端口的输入导纳，Yjk(j≠k)相当于j短路时在端口k处的转移导纳.
2 参数不完全对称的输电线路模型
本文采用集中参数表示三相输电线路模型，将线路首端的母线电压看作电压源，因在高压输电线路中，线路的阻抗参数具有R≪X的特点，其中，R为电路电阻参数，X为测量阻抗参数，同时本文主要研究的是互感与电抗部分不完全相等造成的影响，并且接入的电容元件主要是用来调节线路的互感及电抗参数不对称问题，因此在线路模型中忽略电阻参数的影响.三相输电线路具体模型如图2所示(B为压控转换导纳).
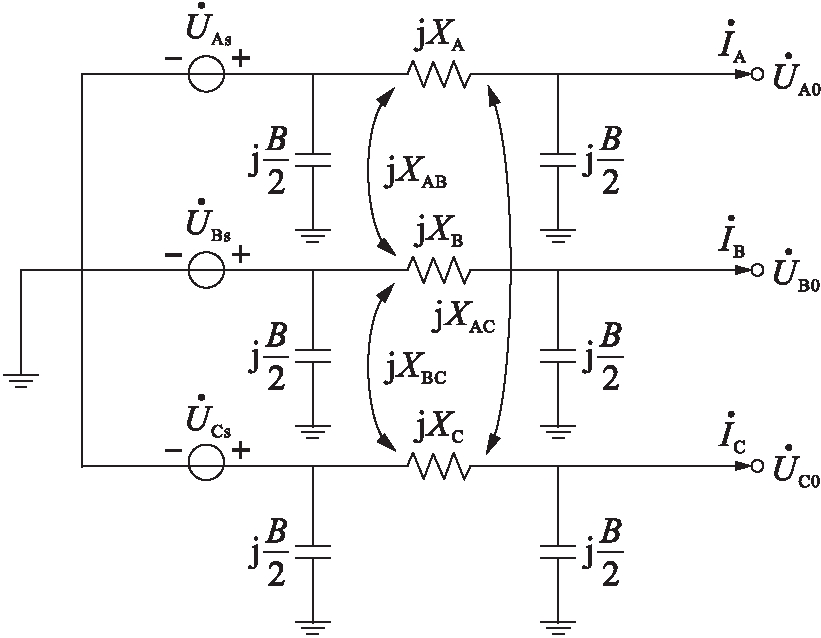
图2 三相输电线路模型
Fig.2 Model for three-phase transmission line
依照广义诺顿定理可写出其诺顿等值电路表达式为
(4)
对于短路导纳矩阵Ysc，首先看在A端口接入电压源，B、C两相短路的情况，其电路结构如图3所示，被短路的元件已略去.
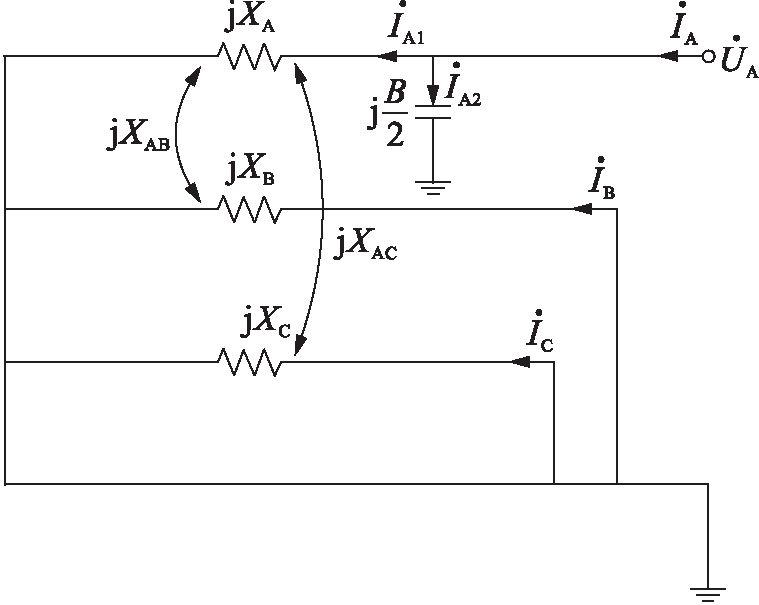
图3 B、C相短路时的电路图
Fig.3 Short circuit diagram of B and C phases
端口B短路时，在端口A的转移导纳为YBA，由B端口的KVL方程
可得
(5)
同理，由C端口的KVL方程
可得
(6)
对于A端口的输入导纳YAA，首先由A端口串联阻抗部分的KVL方程可得
(7)
将式(5)、(6)代入式(7)可得
(8)
表示成压控型伏安关系式为
(9)
式中，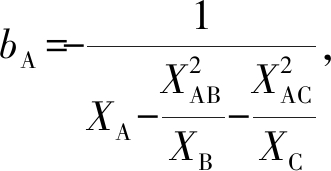
由此可得A端口的输入导纳YAA的表达式为
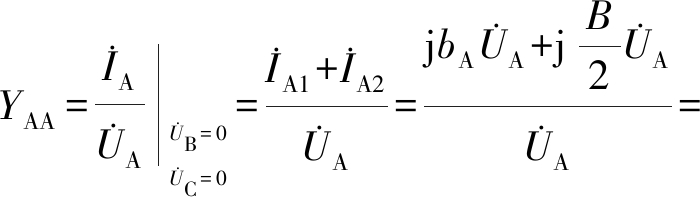
(10)
B、C端口短路时，在A端口的转移导纳为
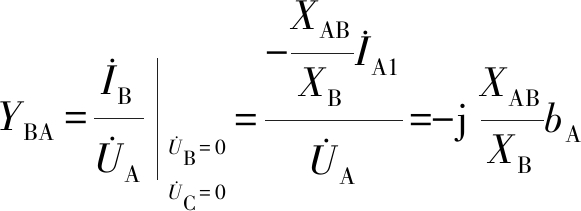
(11)
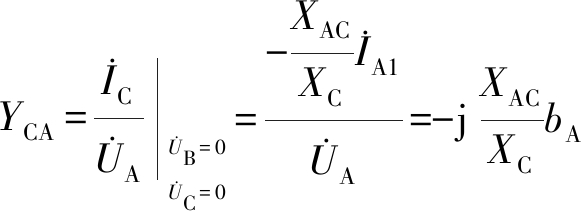
(12)
对于B、C端口可利用同样的方法写出其输入导纳和转移导纳，由此可得出诺顿等值电路中的短路导纳矩阵Ysc为
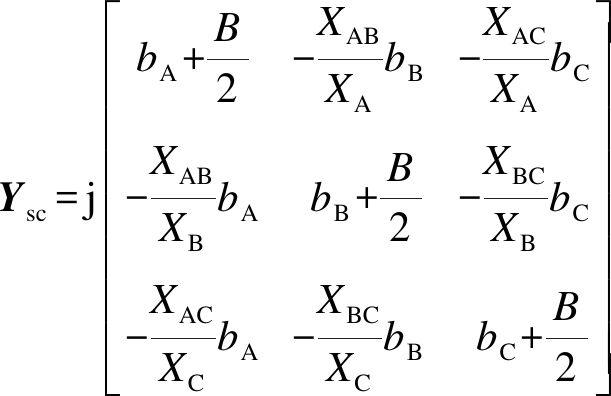
式中：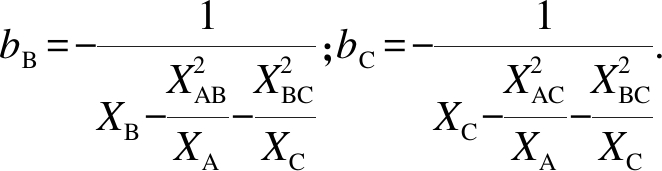
为后续推导方便，将其简记为
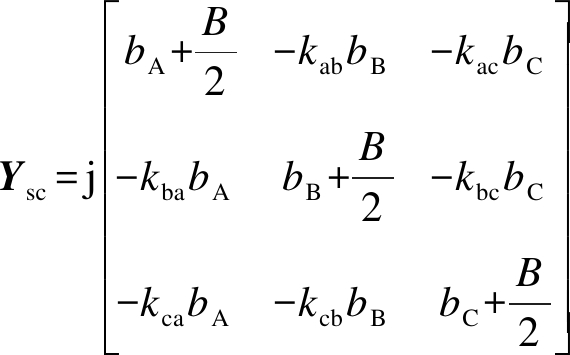
(13)
式(4)中，三相均接地时的短路电流向量
为
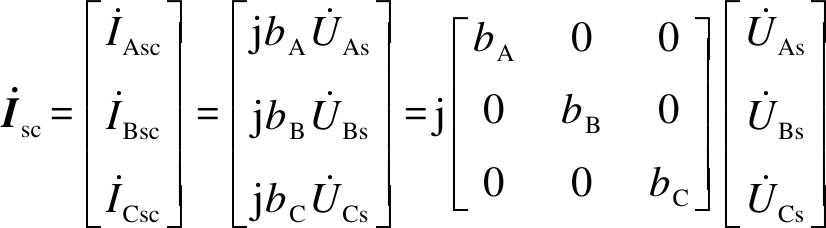
当线路空载时，由式(4)可得
(14)
因此，线路末端空载电压表达式为
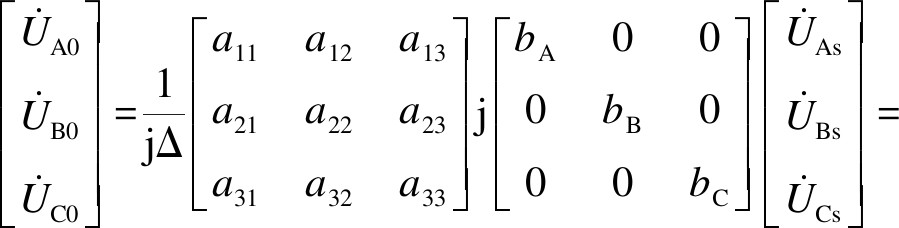
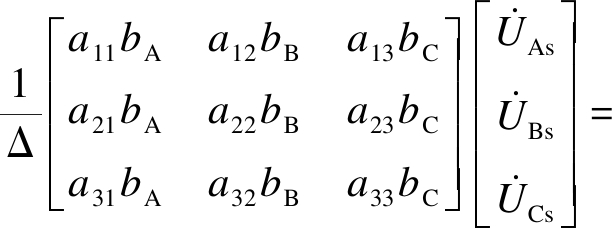
(15)
式中：Δ=|Ysc|；A为Ysc转换矩阵.
由式(15)可知，当线路参数不完全对称，自感与互感部分均不相等，这就导致式(13)中kab、kba、kac、kca、kbc、kcb、bA、bB、bC这些参数都不相等，因此这种不对称经过公式传递将被扩大，进而造成线路电压出现更为严重的不对称现象.此时线路中出现的不对称电压、电流会在线路上产生附加的损耗，并且可能会导致某相线路出现过负荷等问题，严重时还会影响线路两端的发电机和变压器等电气设备.
3 调整线路电压不对称性方法
为改善由于线路参数不对称造成的线路电压不对称的现象，现对线路末端无功补偿的投切量进行适当调节.根据无功补偿设备中电容元件的接入方式，可以得到如图4所示的输电线路模型.三角形接线的无功补偿电容器不仅补偿效果好，而且不受三相电容器容抗不平衡的影响，可对不对称的参数进行调节.
根据图4同样可得出其诺顿等效电路的表达式为
式(16)中，三相均接地时的短路电流向量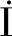
′sc为
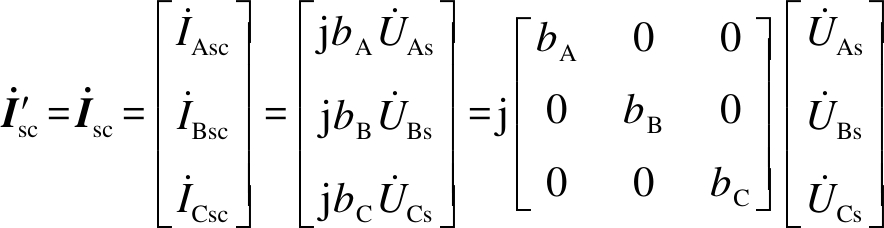
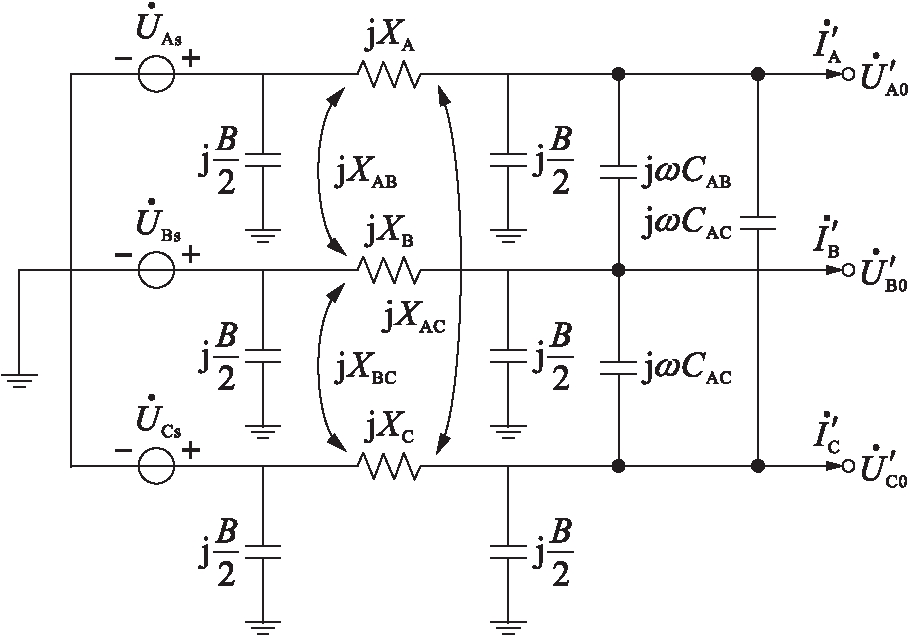
图4 接入并联电容后的输电线路模型
Fig.4 Model for transmission line after parallel capacitor accessing
对于接入了并联电容后的诺顿等值电路中的短路导纳矩阵Y′sc，同样可依照第2节中介绍的方法得出，即
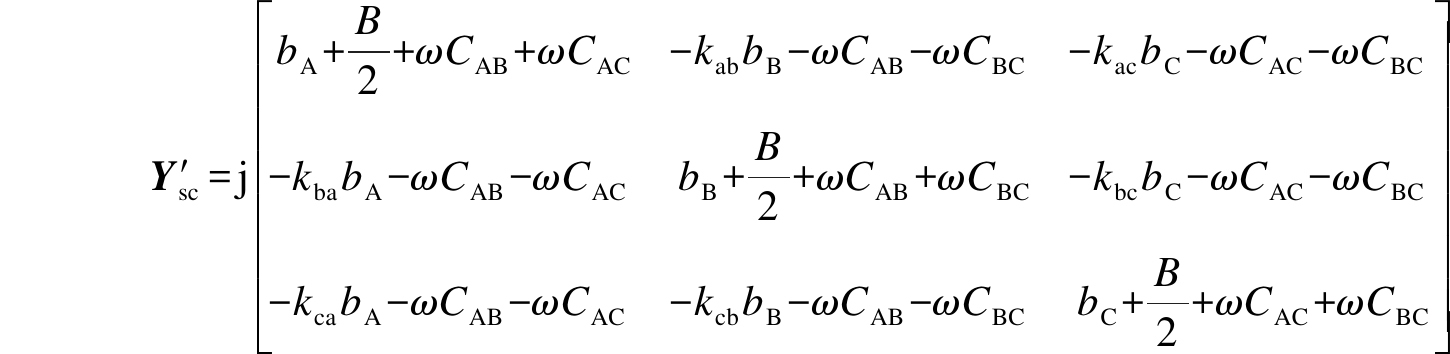
(17)
令C1=ωCAB+ωCAC，C2=ωCAB+ωCBC，C3=ωCAC+ωCBC，则式(17)可化简为
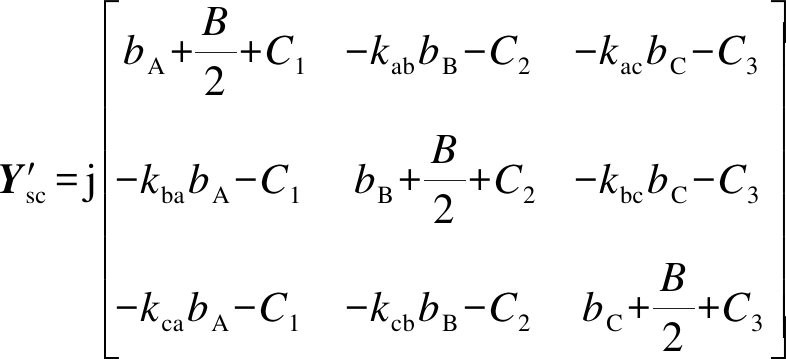
(18)
同理，在线路空载时，可推出线路末端电压的表达式为
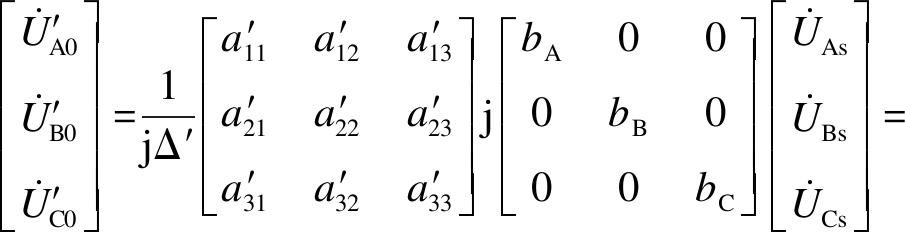
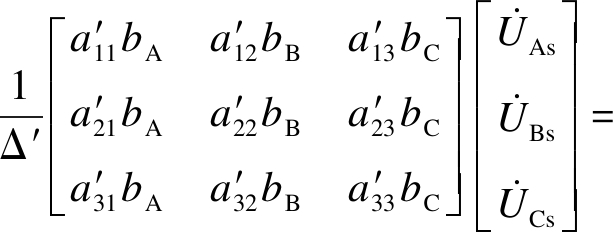
(19)
式中，Δ′=|Y′sc|.由式(19)可以看出，在三相电源对称或不对称度很小的情况下，若要使端口电压接近对称，则需使矩阵A′中主对角元素及非主对角元素分别接近相等，当矩阵A′满足主对角线元素与非主对角线元素分别相等这一条件时，在三相电源对称的情况下，线路末端的电压也将实现完全对称.但通过调节CAB、CAC、CBC的大小可能无法同时满足上述条件.通过对A′中各元素表达式的分析，本文在此选择令A′中主对角线相等来确定CAB、CAC、CBC的大小.
以青海电网月石Ⅰ线的停运测量参数为例，测量参数中R=0.042 5 Ω/km，X=0.452 4 Ω/km，
令XA=0.352 4 Ω/km，XB=0.452 4 Ω/km，XC=0.552 4 Ω/km，同时，根据卡松公式可知，同型号导线同一条件下的自感抗参数大约是互感参数的2～3倍，因此取XAB=0.226 2 Ω/km，XBC=0.226 2 Ω/km，XAC=0.150 8 Ω/km，取线路长度为100 km，由此计算可得
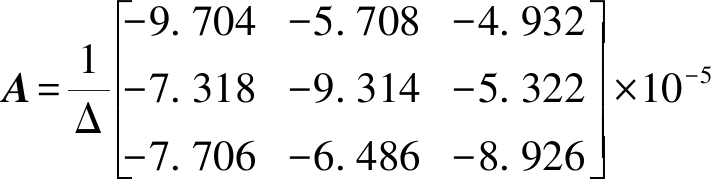
为确定CAB、CAC、CBC的大小，使矩阵A′中的主对角元素接近相等，即a′11bA=a′22bB=a′33bC，解得
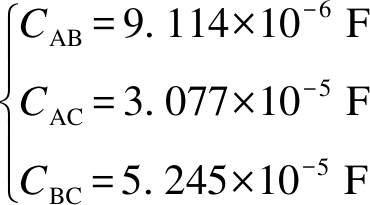
当线路末端变电站内配备有静止无功补偿设备时，假设晶闸管投切电容器TSC每组投切最小容量为3 Mvar，其电容大小约为27.5 μF，因此，在AB相间投入0组电容器，即取CAB=0 F，在AC相间投入1组电容器，即取CAC=27.5 μF，在BC相间投入2组电容器，即取CBC=55 μF.此电容投切值是指在变电站内正常无功补偿投入量的基础上的增加值，所以AB相间的补偿容量并非为零.将其代入矩阵A′，可得
单从矩阵A和A′可以看出，A′中主对角元素和非主对角元素各自间的差异较A中已经小了很多，至于其对线路末端电压不平衡度的改善情况，将通过Matlab仿真结果来验证.
4 仿真验证
在Matlab/Simulink中搭建高压输电线路的仿真模型，其中线路部分采用分布式线路模型，利用其中N×N阶矩阵设定线路的不对称参数.线路中的各相参数值按照第3节中的算例进行设定，线路末端带有三相对称负载.通过PSB模块库中的测量模块和正负零序分量分析模块计算线路末端的正、负、零序电压值，并计算末端电压的负序及零序不平衡度，即
(20)
(21)
当线路首端电源完全对称时，首先在线路负荷为200+j40 MW时，分别对无功补偿投入量调节前后的情况进行仿真，并观察线路末端电压波形，仿真结果如图5所示.
从图5a可以看出，线路参数的不对称已导致线路末端电压波形出现了较为明显的不平衡现象，而进行适当电容补偿调整后，这一不平衡现象可以得到明显的改善，改善后的波形如图5b所示.
逐渐改变线路所带负荷的大小，使线路从接近空载到重载，并分别计算电容补偿调节前后线路末端电压的负序及零序不平衡度，结果如图6、7所示.图6显示随着负荷的增加，线路末端电压负序不平衡度的变化情况；图7显示随着负荷的增加，线路末端电压零序不平衡度的变化情况.
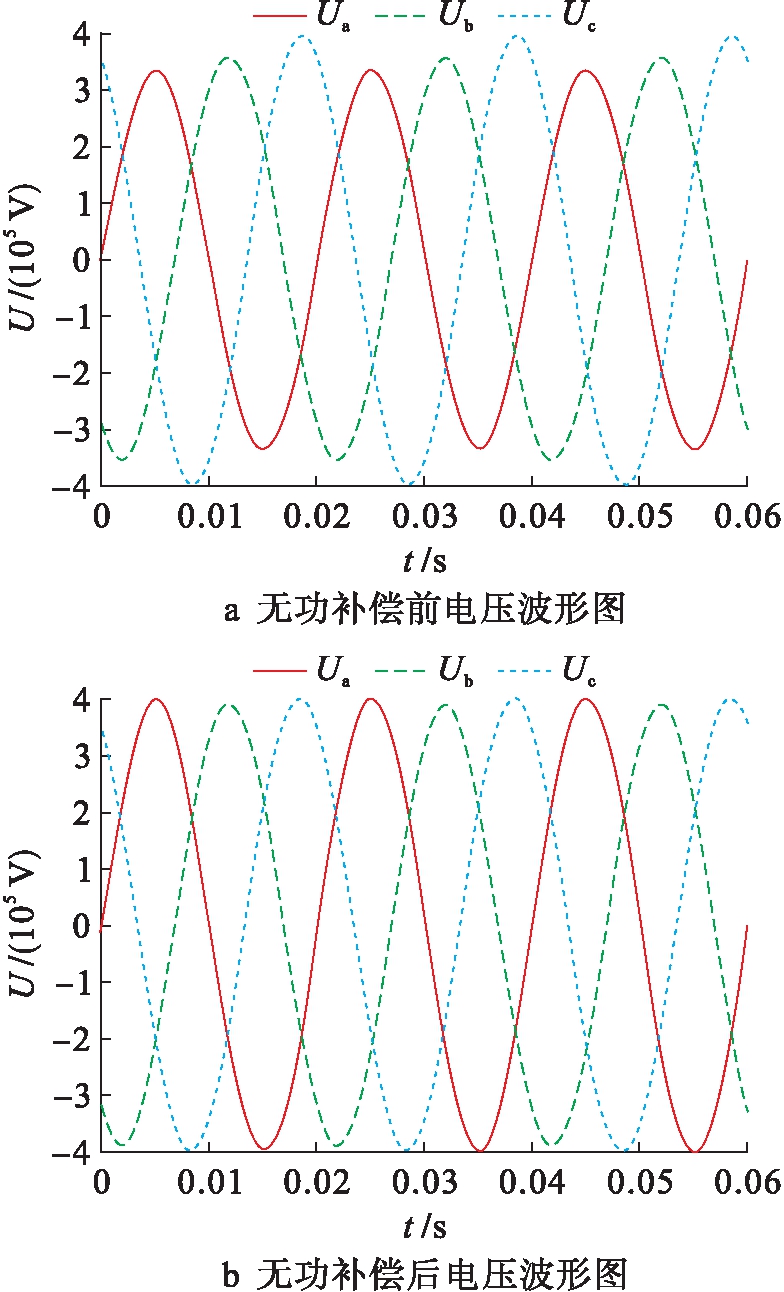
图5 线路电压波形图
Fig.5 Waveform diagram of line voltage
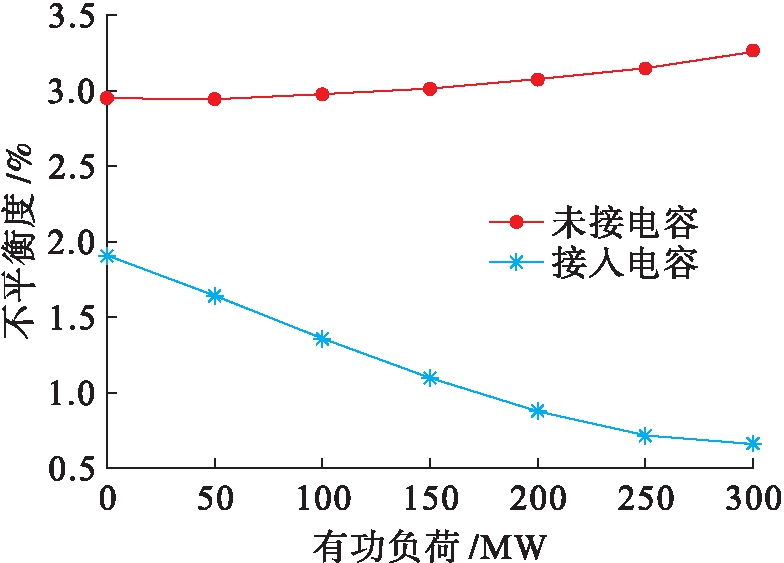
图6 线路电压负序不平衡度
Fig.6 Negative sequence unbalance degree of line voltage
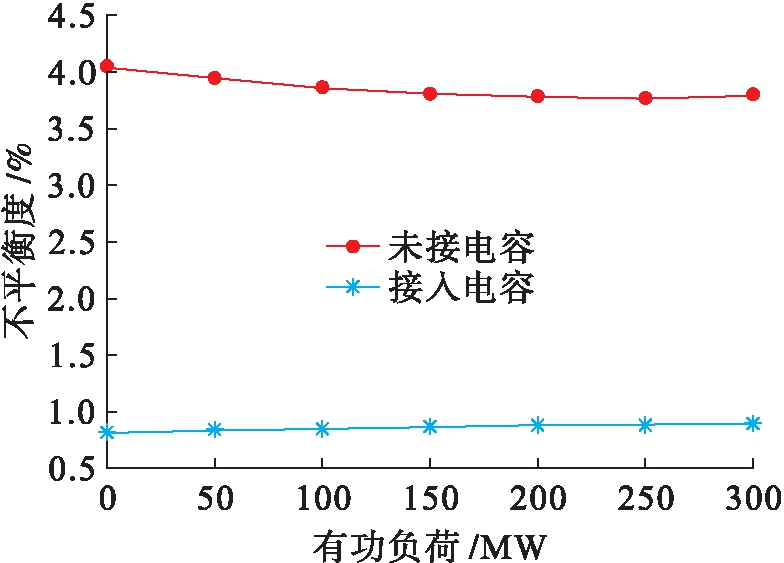
图7 线路电压零序不平衡度
Fig.7 Zero sequence unbalance degree of line voltage
由图6、7可以看出，在未进行电容补偿调节时，线路末端电压的负序不平衡度会随着负荷的增加而增大，零序不平衡度则随负荷的增加呈现基本持平的趋势，并且负序和零序不平衡度均已超过电能质量国标中2%的限值.而进行电容补偿调节后，末端电压的负序和零序不平衡度的数值明显降低，达到国标中规定的电压不平衡度不得超过2%的标准，并且随着负荷的增加，当线路消耗的无功逐渐超过对地导纳发出的无功时，调节效果会更好.其中，对于负序不平衡度的改善程度最大可达79.40%，对于零序不平衡度的改善程度最大可达58.14%，这说明，通过调节无功补偿电容的大小可以降低线路上的不平衡电压，其中负序电压的降低效果更为明显.
5 结 论
本文在广义诺顿定理的基础上，分析了线路参数不对称对线路末端电压的影响，推导出当线路阻抗参数及相间互感参数均不对称时线路首末端电压的关系.
通过调节线路末端变电站内无功补偿电容投切量的大小，使得线路末端电压的不平衡度降到最低，从而改善整条线路的不对称状况.此方法尤其适用于已建成并投入运行后无法改变其相序排列方式的线路.通过Matlab仿真验证了此方法可改善由于线路参数不对称导致的线路电压不平衡状况，在线路轻载和重载时都可有效降低线路末端的不平衡电压.尤其是在线路重载，对地导纳发出的无功小于线路消耗的无功时，此方法的调节效果更好.
[1]林海雪.电能质量指标的完善化及其展望 [J].中国电机工程学报，2014，34(29)：5073-5079.
(LIN Hai-xue.Perfecting power quality indices and prospect [J].Proceedings of the CSEE，2014，34(29)：5073-5079.)
[2]刘前进，朱庆钢，罗龙波.750 kV同塔双回不换位线路电流不平衡度研究 [J].电力系统保护与控制，2013，41(18)：105-110.
(LIU Qian-jin，ZHU Qing-gang，LUO Long-bo.Ana-lysis on current imbalance of un-transposed 750 kV double-circuit lines on the same tower [J].Power System Protection and Control，2013，41(18)：105-110.)
[3]李斌，李学斌，丁茂生，等.特高压同杆双回线的环流不平衡及其影响 [J].电工技术学报，2012，27(4)：202-208.
(LI Bin，LI Xue-bin，DING Mao-sheng，et al.Circulating unbalanced current and its influence of double-circuit UHV transmission lines [J].Transactions of China Electrotechnical Society，2012，27(4)：202-208.)
[4]王晓彤，班连庚，项祖涛，等.换位形式对1 000 kV同塔双回线路感应电压和电流的影响 [J].电力建设，2015，36(5)：37-44.
(WANG Xiao-tong，BAN Lian-geng，XIANG Zu-tao，et al.Influence of transposing form on induced voltage and current in 1 000 kV double-circuit transmission lines [J].Electric Power Construction，2015，36(5)：37-44.)
[5]靳希，吴文辉，吴世敏.基于戴维南等值的输电线路不平衡度分析新方法 [J].电力系统保护与控制，2011，39(21)：7-11.
(JIN Xi，WU Wen-hui，WU Shi-min.New methods of analysis of the unbalanced degree of the transmission line based on Thevenin equivalent [J].Power System Protection and Control，2011，39(21)：7-11.)
[6]全国电压电流等级和频率标准化技术委员会.GB/T 15543-2008电能质量三相电压允许不平衡度标准 [S].北京：中国电力出版社，2008.
(National Voltage Current Grade and Frequency Standar-dization Technical Committee.GB/T 15543-2008 Power quality three-phase voltage unbalance [S].Beijing：China Electric Power Press，2008.)
[7]高岩，尹建华，陈晓科，等.基于环型电网的输电线路相序排列方法研究 [J].电力系统保护与控制，2017，45(14)：92-97.
(GAO Yan，YIN Jian-hua，CHEN Xiao-ke，et al.Research of phase sequence arrangement of transmission lines in the loop network [J].Power System Prote-ction and Control，2017，45(14)：92-97.)
[8]周冠波，李晓华，蔡泽祥，等.同杆多回线路不平衡问题分析与对策 [J].电力系统自动化，2010，34(16)：58-63.
(ZHOU Guan-bo，LI Xiao-hua，CAI Ze-xiang，et al.Analysis and countermeasures for the unbalance prob-lem of multi-parallel line on the same tower [J].Automation of Electric Power Systems，2010，34(16)：58-63.)
[9]陶凯，刘明波.输电线路不换位引起的不对称问题及其改进方法 [J].电力系统保护与控制，2010，38(16)：39-43.
(TAO Kai，LIU Ming-bo.Asymmetric issues caused by un-transposed transmission lines and its solution [J].Power System Protection and Control，2010，38(16)：39-43.)
[10]李永坚，黄绍平，许志伟，等.不换位高压线路分相建模研究及其不平衡性分析 [J].电力系统自动化，2010，34(19)：75-80.
(LI Yong-jian，HUANG Shao-ping，XU Zhi-wei，et al.Research of individual phase modeling of un-transposed high voltage transmission lines and analysis of its unbalanced operation [J].Automation of Electric Power Systems，2010，34(19)：75-80.)
[11]梁贵书.电网络分析选论 [M].保定：华北电力大学，2005：113-114.
(LIANG Gui-shu.Analysis of network analysis [M].Baoding：North China Electric Power University，2005：113-114.)