环境污染、能源危机成为人类亟待解决的问题，大力发展风电成为缓解这一问题的有效途径.但受研发水平和机械传动损失等因素的影响，目前风力机发电效率远没有达到Betz理论的极限值.风轮作为实现风能
机械能转换的关键环节，其风能捕获能力决定了风力发电机组输出功率，除翼型外，桨距角、转速、锥角等因素均对风轮风能捕获能力产生显著影响.由于风力机翼型起源于航空翼型，因此风力机翼型设计一直沿用航空翼型的设计理念.受该设计理念影响，对风力机叶片攻角的传统设计也普遍采用航空器设计攻角，即采用最大升阻比攻角[1-2].目前针对风力机叶片攻角的研究虽有报道[3-5]，但尚未对是否风力机叶片同航空器一样在最大升阻比攻角时具有最大的能量利用效率进行论证.而通过调节风轮锥角来提高风轮风能捕获能力的研究国内外均未见报道.
本文对风力机叶片攻角α及风轮锥角β进行优化，并对α与β之间的相关性做进一步研究，为进一步设计新型更高效风力机提供最佳的优化方案.采用两套优化方案对NACA0012翼型的1.5 MW风力机α、β角进行实例优化，方案1对α、β进行独立优化：首先应用传统叶素动量(BEM)理论对叶片攻角α进行优化，确定α的最佳工作点，再在该最佳工作点处，应用对β锥角修正所得的β-BEM理论进一步对锥角β进行优化，计算优化后风能利用系数Cp1.方案2对α、β角进行统一优化：应用β-BEM理论同时对α、β角进行优化，计算优化后风能利用系数Cp2.通过对Cp1与Cp2进行对比分析，研究α、β之间相关性，并确定最佳优化方案.
1 传统叶素动量理论
1.1 贝茨理论模型
图1为Betz理论的气流图.在风轮上游远端处，风速为υ0，气流截面积为S0；风轮处，风速为υ，气流截面积为S；风轮下游远端处，风速为υ1，气流截面积为S1.由Betz理论[6]可知，当满足式(1)，即
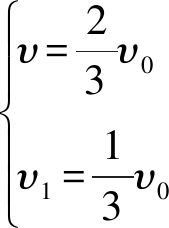
(1)
风轮吸收功率达到最大值
风能利用系数Betz极限为
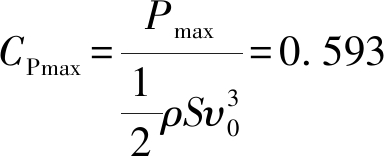
(2)
式中，ρ为空气密度.风力机工作于低风速环境下，此时气流视为不可压缩流体，式(1)结合连续性方程S0υ0=Sυ=S1υ1得
S0∶S∶S1=1∶2∶3
(3)
式(3)说明风轮上、中、下游的气流截面积逐渐增大，表明在风轮处气流除具有平行于风轮旋转轴的轴向速度外，同时具有垂直于旋转轴的径向速度分量，这为进一步引入风轮锥角β提供了依据.
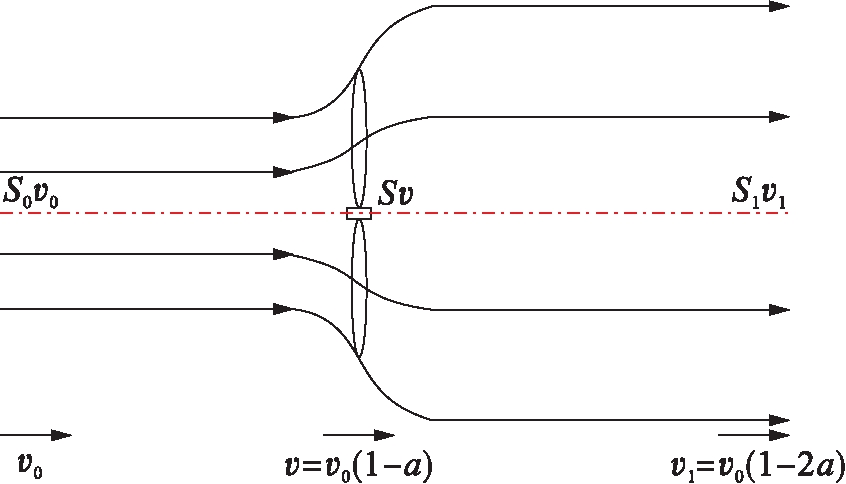
图1 贝茨理论风轮气流图
Fig.1 Airflow of wind wheel in Betz theory
1.2 传统叶素动量理论
叶素动量理论一直是研究风力机气动特性的有效方法，相关研究在文献中多有报道[7-9].传统的叶素动量理论采用零锥角模型(β=0°)，即风轮旋转面与旋转轴垂直，此时风轮处气流的径向速度分量与旋转面平行，对风轮不产生转矩作用，因此只考虑气流轴向速度对风轮产生的转矩作用.
由动量理论可知，气流作用在风轮根部距离r处时叶素的轴向推力dFn和转矩dM分别为
(4)
dM=4πρωυ0a′(1-a)r3dr
(5)
式中：a为轴向诱导因子；a′为周向诱导因子；ω为转速.同时，由叶素理论可得到
(6)
(7)
式中：Nb为叶片数；c为叶素弦长；CL、CD为风力机翼型升力、阻力系数；φ为入流角，其表达式为
(8)
式中，λ为当地速度比，其表达式为
(9)
对于某确定的翼型，CL、CD主要由攻角α决定，其表达式为
α=φ-θ
(10)
式中，θ为节距角.
分别将式(4)、(6)及式(5)、(7)建立等量关系，并引入普朗特叶尖损失因子f，可计算出轴向诱导因子a及周向诱导因子a′为
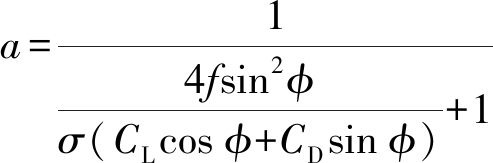
(11)
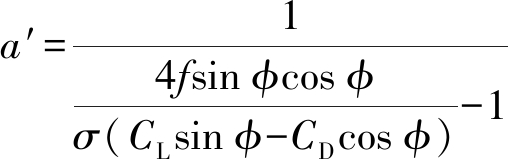
(12)
式中，σ为实度，其表达式为
(13)
进一步结合式(2)、(7)计算出风能利用系数为
Cp=σλ[(1-a)2+λ2(1+a′)2]·
(CLsin φ-CDcos φ)
(14)
给定当地速度比λ及节距角θ，通过迭代式(8)～(13)计算出a、a′的收敛值，并进一步由式(14)计算出风能利用系数Cp.
2 基于锥角β的BEM修正理论
传统BEM理论模型中没有涉及到锥角β，因此，若要对β实现优化，须对传统BEM理论进行β修正.图2为将β引入到传统叶素动量理论后的气流分布示意图，此时风轮旋转面为圆锥面，气流在与旋转轴垂直平面内的径向速度分量与风轮旋转圆锥面不平行，因此，径向速度分量亦将对风轮产生转矩作用，进而转换为风轮输出功率.
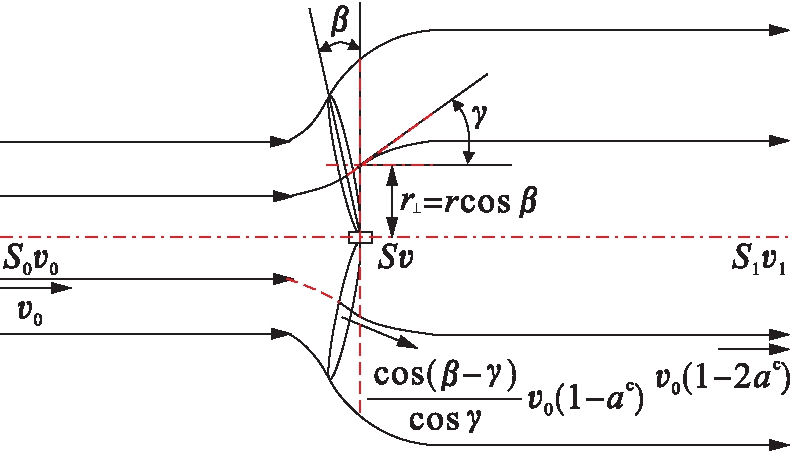
图2 β锥角时风轮气流分布
Fig.2 Airflow distribution of wind wheel with cone angle β
如图2所示，取与叶根距离为r的风轮叶素，其距离旋转轴的垂直距离为
r⊥=rcos β
(15)
气流速度与风轮旋转锥面垂直的速度分量υ⊥为
(16)
式中：γ为气流发散角，表示气流流线与旋转轴夹角；ac为对轴向诱导因子a的修正值.
将修正式(15)、(16)及β代入传统BEM理论表达式(4)～(14)中，得到修正后β-BEM理论表达式为
(17)
dMc=4πρωυ0a′c(1-ac)r3cos4βdr
(18)
CDsin φc)cos βdr
(19)
CDcos φc)rcos2βdr
(20)
(21)
(22)
αc=φc-θ
(23)
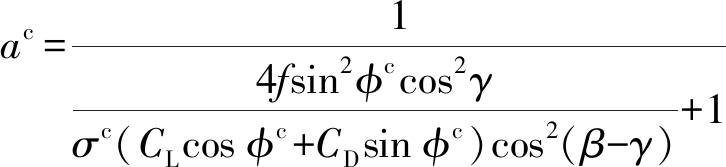
(24)
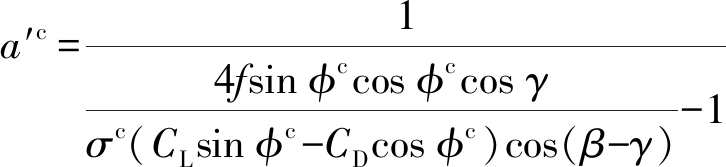
(25)
(26)
(CLsin φc-CDcos φc)
(27)
β-BEM理论表达式(17)～(27)在风轮锥角β=0°时与修正前表达式(4)～(14)完全一致，说明β-BEM理论表达式具有较强的通用性.
3 α、β独立优化
3.1 NACA0012翼型风力机的α优化
为实现方案1中对α的优化，采用BEM理论对NACA0012翼型的1.5 MW风力机CP值进行数值计算.该翼型为NACA经典翼型，低风速时，该翼型的特性曲线如图3所示，在小攻角段，CL与α几乎成正比关系，在12°攻角时翼型发生失速，通常情况下，翼型均工作在失速点之前.
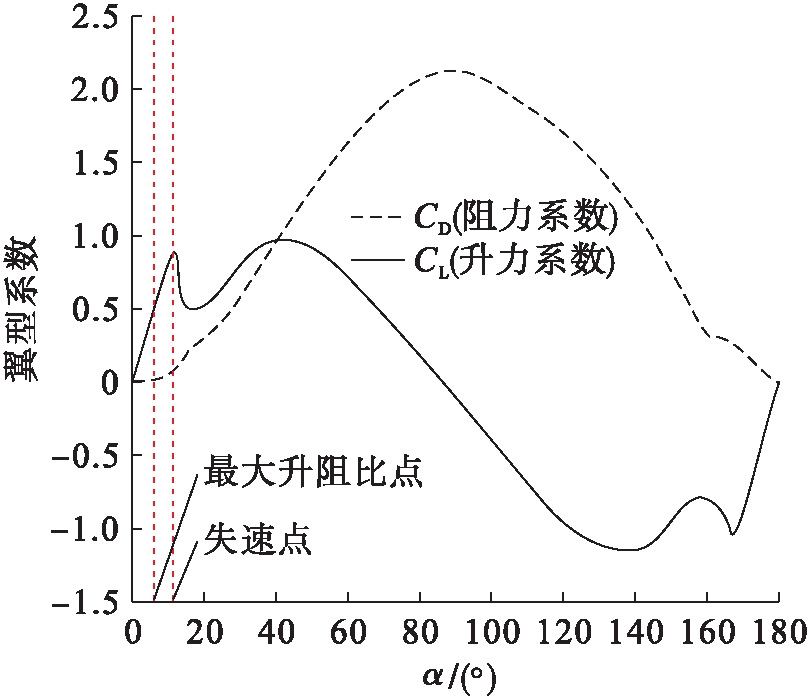
图3 NACA0012翼型特性曲线
Fig.3 Characteristic curves of NACA0012 airfoil
选取翼型中部叶素作为计算区域时，不涉及叶尖损失，因此叶尖损失因子f取1.将λ、θ做为循环变量，对于每一组λ、θ，通过式(8)～(13)迭代求解各参数，进一步代入式(14)计算CP，最终得到CP随λ、θ变化的曲面图.使用C++语言编写该迭代程序，对6万组λ、θ点的CP值进行计算，近似得到了CP与λ、θ之间的连续变化关系如图4所示.曲面最高点处λopt=4.02，θopt=4.0°，CP-opt=0.482，攻角αopt=5.9°，该点即为最佳工作点，αopt即为最佳攻角(opt下标表示最佳工作点).
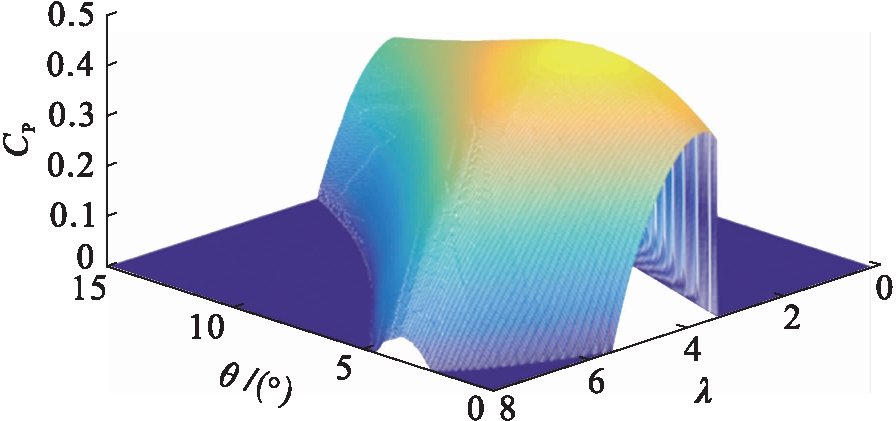
图4 CP、λ、θ曲面图
Fig.4 Surface diagram of CP，λ and θ
进一步将采用最佳工作点与采用最大升阻比工作点的CP值做比较.在图4中分别提取攻角α等于最佳攻角(α=αopt=5.9°)和最大升阻比攻角(α=αmldr=4.2°)的各数据点，构成两条等攻角曲线，分别称之为最佳攻角曲线和最大升阻比攻角曲线，两者对比图如图5所示.
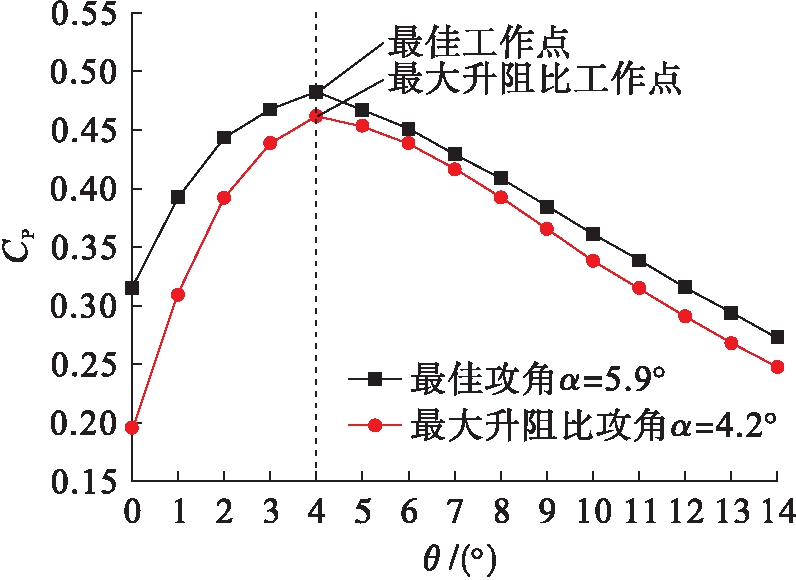
图5 最佳攻角与最大升阻比攻角时CP对比
Fig.5 Comparison of CP at optimum attack angle andattack angle with maximum lift-drag ratio
由图5可见，在其它因素相同的条件下，采用最佳攻角比采用最大升阻比攻角的CP值显著提高.两曲线CP值均在θ=4°时达到极大值，两极值点分别称为最大升阻比工作点和最佳工作点，对应CP值分别为0.462 0和0.482 1.可见最佳工作点比采用最大升阻比工作点时，CP提高了4.3%.
计算结果同时表明，采用最佳工作点时，当地速度比λ由原采用最大升阻比工作点时的4.7降为4.0，减小15%.这说明在不改变风轮其它运行参数的条件下，转速降低15%，可使风力机由最大升阻比工作点调整到最佳工作点.
3.2 NACA0012翼型风力机的β优化
对锥角β的优化须使用β-BEM理论，在攻角优化所确定的最佳工作点处(θ=4.0°，λ=4.0)，进一步通过β-BEM对风轮锥角β进行优化.同样选取翼型中部叶素作为计算区域，对多组锥角β、发散角γ对应的风能利用系数修正值
进行数值计算.将(β，γ)作为循环变量，通过式(21)～(25)迭代确定诱导因子修正值ac及a′c，进一步通过式(27)计算出风能利用系数修正值
遍历(β，γ)结束后，得到随(β，γ)的变化关系，进一步通过CFD仿真确定出发散角γ，从而得到随β的单变量变化关系，最终确定极大值点及β最优值.
使用C++语言编写迭代程序，β取值范围为[0°，30°]，γ取值范围为[0°，20°]，步长均为1°，迭代后得到
随着β的变化曲线如图6所示.
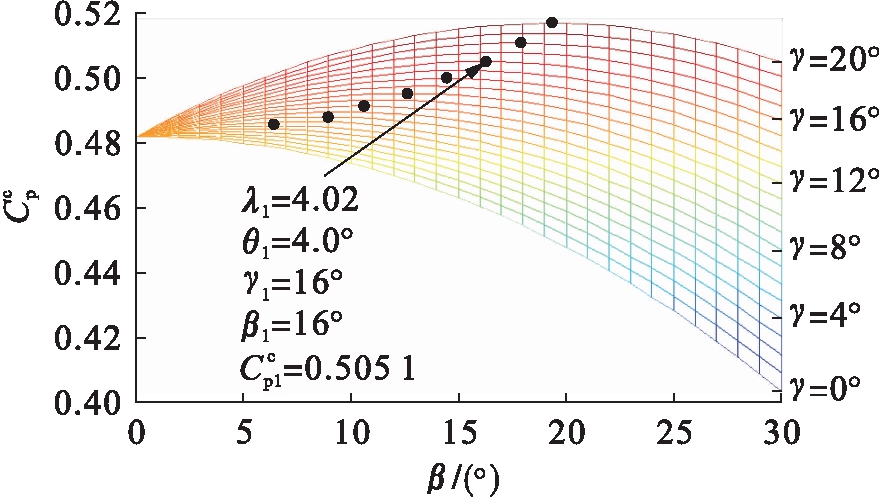
图6 α、β独立优化
曲线簇
Fig.6 Curve cluster of after independent optimization of α and β
由图6可见，每个确定的气流发散角γ对应一条
曲线，所有的γ取值对应一组曲线簇.曲线簇中各曲线的共同特点为：随着β增加均呈现先增加后减小的变化特征.
各曲线在β=0°处汇聚于一点，该点值为0.482 1，与α的优化结果一致，这与传统BEM理论风轮旋转面为平面时的计算结果相符，从侧面证明了该修正后β-BEM理论的正确性.
为确定该风力机具体工作于图6中哪一条曲线，采用CFD仿真确定发散角γ.CFD作为流体力学仿真软件在风力发电领域得到广泛应用[10-11].仿真结果表明，叶片中部气流发散角γ=16°.可知该曲线在β=16°时取得极值
与β优化前的0.482 1相比，提升4.8%，而与α优化前的传统最大升阻比工作点的Cp值0.462 0相比，提升9.3%.可见，对α、β进行独立优化极值点处各参数分别为：
4 α、β的统一优化
为实现优化方案2中对α、β的统一优化，将β、γ、λc、θ四参数在迭代程序中进行统一考虑.程序流程图如图7所示.
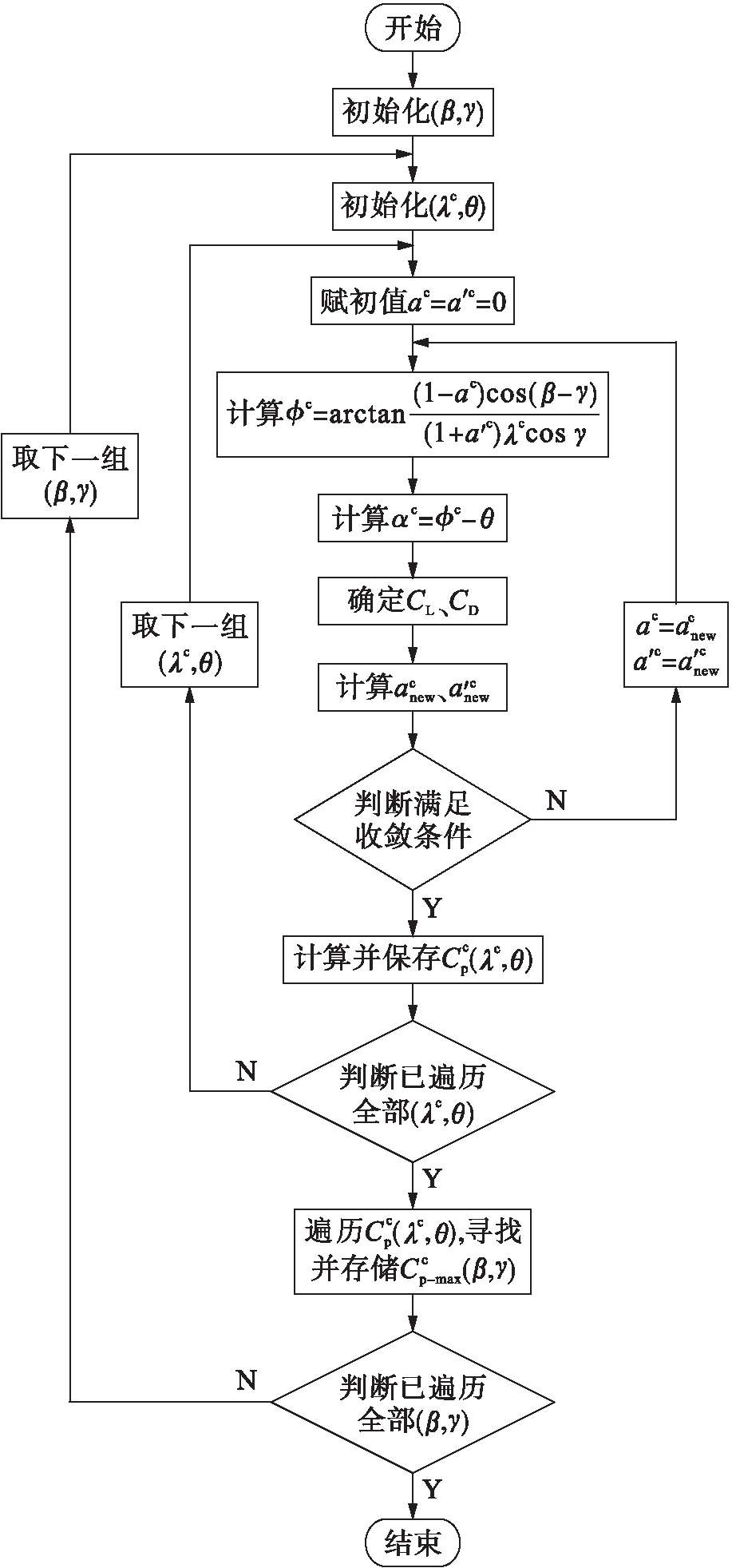
图7 α、β统一优化程序流程图
Fig.7 Flow chart of procedure for unified optimization of α and β
将(λc，θ)参数组作为内层循环变量，将(β，γ)参数组作为外层循环变量.通过式(21)～(25)迭代确定诱导因子修正值ac及a′c，并通过式(27)计算出风能利用系数修正值
内层循环(λc，θ)每遍历一次，搜寻该次遍历所得风能利用系数最大值
其为关于(β，γ)的函数.当外层循环遍历(β，γ)全部结束后，得到
随β变化曲线簇.进一步通过CFD仿真确定处发散角γ，从而得到随β的单变量变化关系，最终在极大值点处取得β最优值.
使用C++语言编写该迭代程序，θ取值范围[0°，30°]，步长1°，λc取值范围[0.1，8]，步长0.25，β取值范围[0°，30°]，步长为1°，γ取值范围[0°，30°]，步长为1°，迭代后得到
曲线如图8所示.
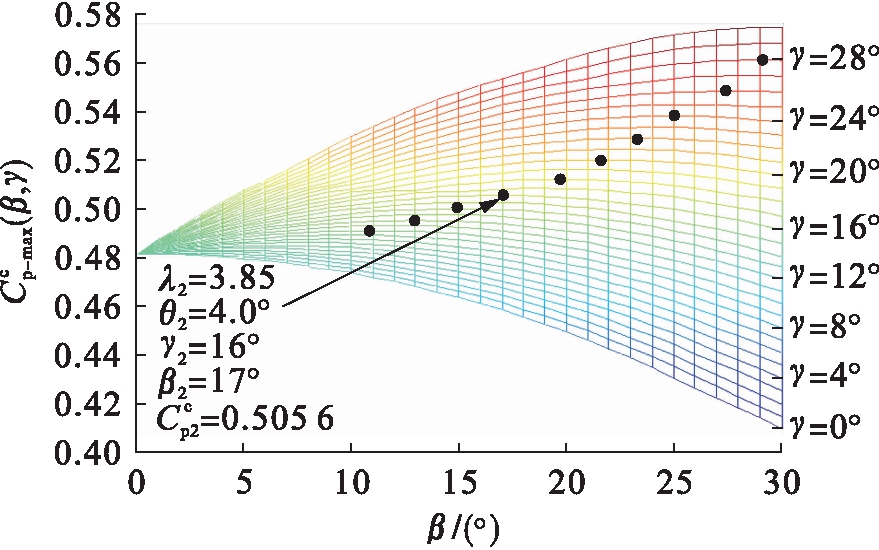
图8 α、β统一优化
曲线簇
Fig.8 Curve cluster of after unified optimization of α and β
由图8可见，对α、β进行统一优化极值点处各参数分别为：
比优化前采用传统最大升阻比工作点Cp提升9.4%.
5 结 论
分别采用对α、β的独立优化方案和统一优化方案对NACA0012翼型的1.5 MW风力机α、β角进行实例优化，结果表明：
1) 采用α最佳工作点攻角与采用最大升阻比工作点攻角相比，在其它因素相同的情况下，风力机Cp提高4.3%；在α最佳工作点处继续对β优化，Cp再提高4.8%.
2) 对α、β进行独立优化，极值点处各参数分别为：
提升9.3%.
3) 对α、β进行统一优化，极值点处各参数分别为：
提升9.4%.
α、β具有弱相关性，理论上宜采用统一优化方案，但由于Cp提升率差异不大，故从工程方便角度考虑，仍可以采取独立优化方案.
[1]程江涛，陈进，沈文忠，等.基于最大风能利用系数的风力机翼型设计 [J].机械工程学报，2010，46(24)：111-117.
(CHENG Jiang-tao，CHEN Jin，SHEN Wen-zhong，et al.Design of wind turbine airfoils based on maximum power coefficient [J].Journal of Mechanical Engineering，2010，46(24)：111-117.)
[2]Rajakumar S，Ravindran D.Iterative approach for optimising coefficient of power coefficient of lift and drag of wind turbine rotor [J].Renewable Energy，2012，38：83-93.
[3]汪泉，陈进，王君，等.基于连续攻角的风力机翼型整体气动性能提高的优化设计 [J].机械工程学报，2017，53(13)：143-149.
(WANG Quan，CHEN Jin，WANG Jun，et al.Wind turbine airfoil optimal design with high whole aerodynamic performance considering continuous angle of attack [J].Journal of Mechanical Engineering，2017，53(13)：143-149.)
[4]Thumthae C，Chitsomboom T.Optimal angle of attack for untwisted blade wind turbine [J].Renewable Energy，2009，34：1279-1284.
[5]杨志强，殷明辉，谢云云，等.面向风力机变速运行的叶素运行攻角分布的影响因素分析 [J].中国电机工程学报，2015，35(增刊1)：162-169.
(YANG Zhi-qiang，YIN Ming-hui，XIE Yun-yun，et al.Analysis on factors affecting the distribution of operational angle of attack of blade element for variable-speed operation of wind turbines [J].Proceeding of the CSEE，2015，35(Sup1)：162-169.)
[6]贺德馨.风工程与工业空气动力学 [M].北京：国防工业出版社，2006：80-91.
(HE De-xin.Wind engineering and industrial aerodynamics [M].Beijing：National Defense Industry Press，2006：80-91.)
[7]李德源，池志强，汪显能，等.10 MW风力机叶片设计与动力特性 [J].沈阳工业大学学报，2016，38(3)：241-246.
(LI De-yuan，CHI Zhi-qiang，WANG Xian-neng，et al.Design and dynamic characteristics of blade of 10 MW wind turbine [J].Journal of Shenyang University of Technology，2016，38(3)：241-246.)
[8]de Freitas Pinto R L U，Alves B P F.A revised theo-retical analysis of aerodynamic optimization of horizontal-axis wind turbines based on BEM theory [J].Renewable Energy，2017，105：625-636.
[9]Belloni C S K，Willden R H J，Houlsby G T.An investigation of ducted and open-centre tidal turbines employing CFD-embedded BEM [J].Renewable Energy，2017，108：622-634.
[10]Liu Y C，Xiao Q，Incecik A，et al.Establishing a fully coupled CFD analysis tool for floating offshore wind turbines [J].Renewable Energy，2017，112：280-301.
[11]Giahi M H，Dehkordi A J.Investigating the influence of dimensional scaling on aerodynamic characteristics of wind turbine using CFD simulation [J].Renewable Energy，2016，97：162-168.