随着高速列车技术的兴起,满足人机工程学和空气动力学的流线型列车外形愈来愈受到人们的重视.列车头部外形尺寸的精确性直接影响到列车的速度与安全性,为了精确检测车头外形尺寸,可以把可视化技术应用于标测过程中,从而使动车车头的测量及制造更为精准.在车头标测系统中,散乱点云的三维重建是关键,也是测量系统的基础.
随着激光和结构光的广泛应用,物体的三维点云数据可以通过三维扫描等方式来获得.通过点云数据可以获取被测物体曲面的坐标等相关信息,使得三维曲面重建的过程更加简单,隐函数曲面重建算法[1-3]能更好地根据三维点云数据的特点来重建高精度、高质量的物体模型.
当前的三维重建可以分为三类:1)参数曲面重建;2)变形重建;3)网格重建.高速列车车头的表面结构不是规则的曲面,很难用原有的方法对其进行三维重建.隐函数曲面重建仅仅根据被测物体的三维坐标便能较好地拟合出被测物的三维模型,其中,泊松曲面重建[4-6]可以把点云数据的曲面重构转化为求解泊松方程的问题.泊松曲面重建算法可以很好地运用被测物的整体三维点云数据,从而更好地过滤掉一些与重建计算无关的信息,比较适用于解决数据量较大的离散数据.但是由于车头测量环境限制的原因,采集到的点云样本中含有大量的异常点,现有的泊松曲面算法很难解决车头测量实际应用中去噪的问题,本文对原有方法进行改进,从而有效解决了此问题.原有泊松曲面算法还存着空洞性的问题,本文采取改变罚函数的方法来改进现有的泊松曲面重建方法,从而更好地解决了曲面收缩和曲面空洞等问题,使其表面更加光顺.针对提取等值面时曲面连接的不唯一性,本文提出一种改进算法来消除其二义性.
1 泊松算法
首先要找到一个合适的泊松方程,将这个方程作为求取曲面的隐式函数[7-9],然后再求取点云数据最佳等值面,运用插值的方法去逼近被测物表面,图1为具体的求解示意图.具体步骤如下:1)求取一个最佳的指数函数φM,如果目标点不在曲面内,则该指示函数值就为0;如果目标点在曲面内,则该指示函数值就为1.2)计算指示函数梯度,指示函数的梯度为被测物表面在其中一点的法矢,仅在所求曲面内的法矢可能有非零值,所以通过梯度值[10-11]的计算可以准确定位一点在坐标系中的相对位置.3)运用插值法使指示函数梯度最佳逼近点云的向量场.4)求取所求指示函数相应的等值面即为模型表面.
求取模型表面∂M的最终目标是求取指示函数φM,若点在∂M内,则φM=1;若点在∂M外,则φM=0.若要获得指示函数φM,只要解出![]() 有向点云数据样本中每点的内法线是指示函数的梯度,即
有向点云数据样本中每点的内法线是指示函数的梯度,即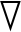 φ=V,解决泊松曲面重建问题的关键就是获取一个指示函数,使该函数的梯度值与三维点云数据的向量场相匹配.
φ=V,解决泊松曲面重建问题的关键就是获取一个指示函数,使该函数的梯度值与三维点云数据的向量场相匹配.
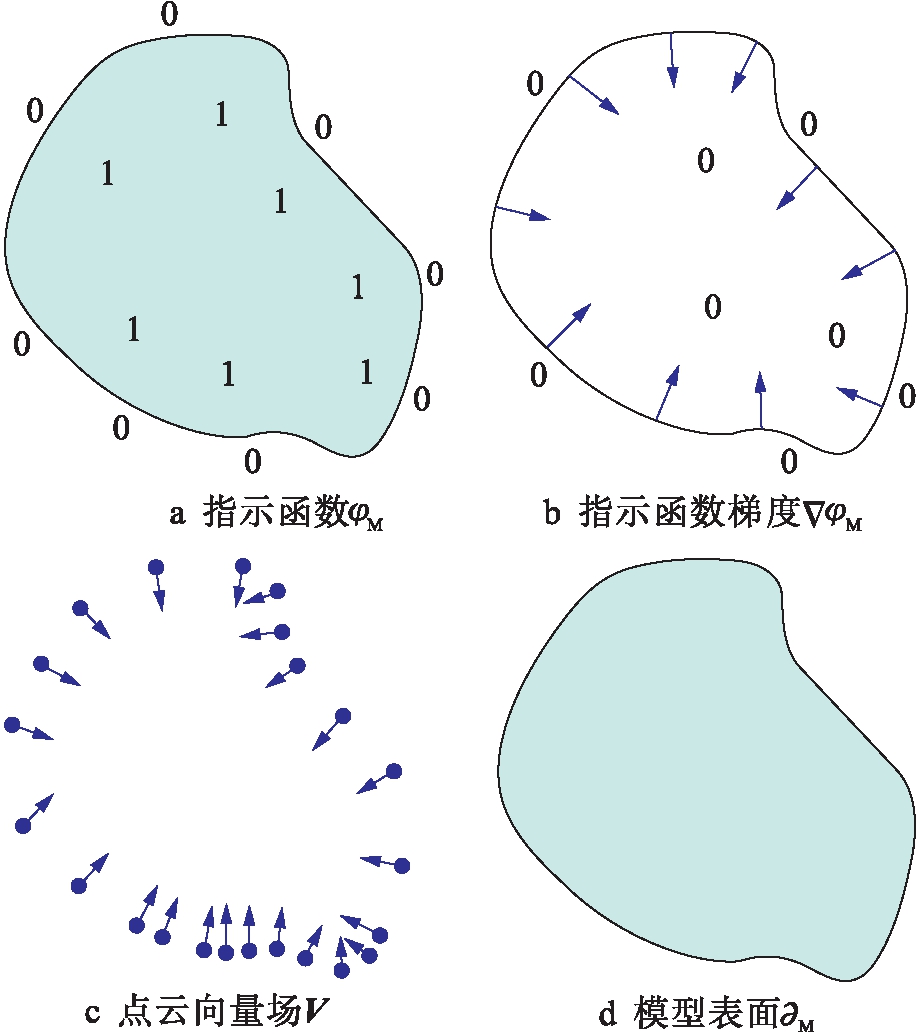
图1 泊松曲面求解示意图
Fig.1 Schematic diagram of Poisson surface solution
2 改进的泊松曲面重建算法
本文基于泊松曲面重建算法,在其点云数据预处理问题、最小化问题与提取等值面问题方面提出了不同的解决方法.在点云数据预处理方面,本文采用一种混合滤波器来去除点云数据的噪声,有效地提高了重建的精度和效率;在最小化问题方面,现有方法基本使用最小二乘罚常数,本文则利用平方范数作为罚常数,有效地控制了重建时间和曲面精度;在提取等值面方面,本文对原有算法[12]进行了改进,消除了原有算法中二义性对提取等值面的影响,获得了比较精确的车头表面三维模型.改进后的重建算法流程如图2所示.
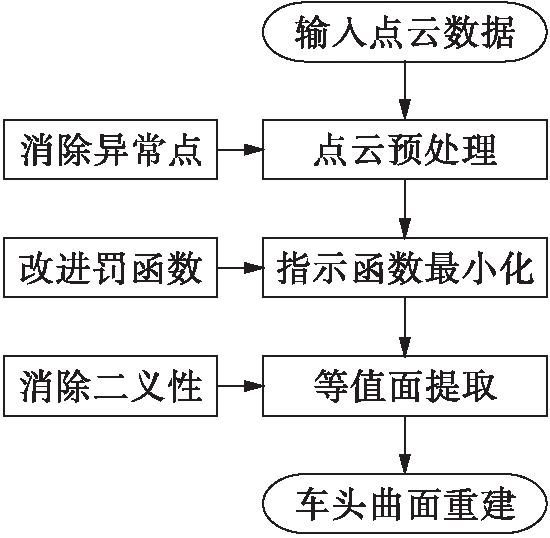
图2 改进算法流程图
Fig.2 Flow chart of improved algorithm
2.1 点云数据预处理改进
现有的泊松曲面重建算法多是采用一些较小的三角面片去拼接被测物的曲面,三维曲面重建模型是由若干个小面片拼接而成,在此模型中,由于测量条件的限制,有很多面片与实际被测物曲面不符.这些面片的顶点对于三维重建模型的精度有着至关重要的作用,这些与被测物原始表面不符的面片散落在车头模型的外部,与被测模型表面相聚较远,不符合点云的正态分布,所以对于原始点云的预处理是很有必要的.
由于车头外形尺寸比较大,点云数据量较大,点云数据的噪声种类也比较多,一般的滤波器很难满足预处理要求.本文将高斯滤波器与中值滤波器相结合,可以更好地对原始点云进行预处理,提高重建模型精度,减少点云的数据量,从而加快处理速度.该种混合型滤波器结合了两种滤波器的优点对原始数据进行去噪,高斯滤波器能最大限度地保持原始点云中各点之间的差异,使得重建车头模型最大限度地保持原貌.中值滤波器可以对测量到的三维点云数据进行较好的平滑处理,大量减少离散点,将不符合被测曲面的点对重建效果的影响降到最低.
解决噪声点的关键是根据所测点云中每一个点的三维坐标值去滤除那些不符合正态分布的点.本文采用的混合滤波器表达式为![]() 其中:d为点云数据中点到X轴的距离;δ为标准方差;w为半峰宽度值.然后利用该滤波器对每一个邻域内的点进行输出,所得点的纵坐标即为输出结果.
其中:d为点云数据中点到X轴的距离;δ为标准方差;w为半峰宽度值.然后利用该滤波器对每一个邻域内的点进行输出,所得点的纵坐标即为输出结果.
2.2 最小化问题的算法改进
改进的泊松曲面重建算法主要为求解指示函数φM的最小化问题,即
式中:x为任意点云;α为正值模型参数;n为点云相关法线;f为可微罚函数,其表达式为
其中:ε为阈值;v为罚函数的自变量.
现有方法多采用最小二乘法进行处理,但最小二乘法需要对较小结构进行收缩,并对较为尖锐的边缘进行平滑处理.而采用平方范数当作罚函数相比于最小二乘法可省去上述过程,该方法可以改善其他罚常数所产生的不稳定性,从而提高了算法效率与重建精度.
2.3 提取等值面问题的算法改进
在泊松重建算法中,如果值为1的角点和值为0的角点位于对角线的两端,则会产生二义性的问题,本文提出一种解决此问题的算法,算法流程图如图3所示.
图3 消除二义性流程
Fig.3 Flow chart for elimination of ambiguity
利用泊松曲面重建算法提取等值面时,需逐点判断各个面片是否存在两种连接方式.将各个顶点函数值与等值面阈值进行比较,大于阈值的点记为1,小于阈值的点记为0.在同一个小面片中,若值为1和0的点分别位于对角线的两端,则存在两种连接方式,存在二义性的可能.图4为两种连接方式产生的二义性示意图.
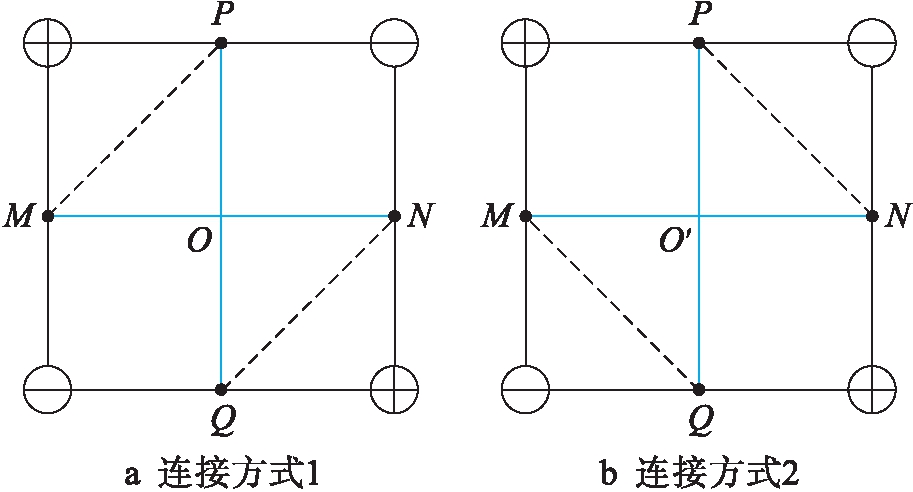
图4 二义性示意图
Fig.4 Schematic diagram of ambiguity
设点P、Q、M、N为等值面与二义性面的交点,直线PQ和MN的交点为O.计算并比较交点处的函数值与等值面阈值的数值关系,若大于等值面阈值,记为1,反之为0.若为1,该面片与标记为1的顶点在一个区域;反之,与为0的两个顶点在一个区域,这样,可以确定唯一一个等值面连接方式,从而消除了二义性的问题.
通过拼接获取曲面重建后的车头三维表面模型,并把面片拟合起来并将其曲面化,从而将抽象的车头点云数据转化为可视化的三维模型,形成光滑的三维曲面并进行测量等操作.
3 实验结果及分析
为了验证本文算法的可行性和有效性,将本文算法与现有算法进行对比.实验平台为Windows 10 64位系统,在Visual Studio 2010与PCL点云库1.6.0环境下进行实验.采用实验室已有扫描获得的车头点云数据进行验证,实验结果表明,本文算法对于高速列车车头表面重建取得了较好的结果,算法具有鲁棒性和高效性.
图5为通过机器视觉方法得到的车头三维点云模型(stl文件),图6为采用改进方法对其进行重建的三维模型.实验结果表明,通过改进算法重建得到的三维模型虽然在一些较小的细节上不清晰,但是对车头外形曲面的拟合精度高,并且重构曲面广顺度好.

图5 车头的点云数据
Fig.5 Point cloud data of locomotive

图6 重建的模型曲面
Fig.6 Reconstructed model surface
图7a为采用现有泊松曲面重建得到的车头三维曲面模型;图7b为采用本文方法获得的曲面模型.通过对比不难看出,采用本文方法处理过的数据经三维曲面重建后得到的车头模型与现有算法相比有明显差别,其还原效果更为真实,表面更为光滑,重建效果更好.
图8为采用现有算法与本文算法的细节放大对比图.采用本文方法重建后的模型光顺性较好,通过对点云数据的预处理与对提取等值面方法的改进,滤除了大量异常点,减少了错误拼接的可能,各个小面片之间的拼接更为合理,使得整个重建曲面更加光滑,较好地还原了原始车头模型.
表1为改进算法与现有算法各项相关数据的对比,通过预处理点云数据,删除了大量异常点,提高了重建效率.改进算法通过对提取等值面时二义性的消除,减少了小面片错误拼接而导致的空洞性问题,拼接的小面片数量显著增加,拼接更规则,使得重建车头三维模型表面更光滑,重建效果有很大提高.通过对两种算法所得的三维模型与车头原始数据进行表面轮廓度误差计算而得出的数据可以看出,改进算法的轮廓度误差相较于现有算法显著降低,重建精度更高,对车头模型的还原度更好.改进算法通过对大量异常点的滤除与对最小化问题的改进,减少了数据处理量,简化了函数最小化的过程,从而有效缩短算法的运行时间,提高了车头曲面重建的运行效率.

图7 车头外形曲面重建对比
Fig.7 Comparison in reconstructed surfaces of locomotive

图8 车头外形曲面重建细节对比
Fig.8 Detailed comparison in reconstructed surfaces of locomotive
通过对实验数据的分析不难看出,改进算法较现有方法的时间复杂度低,算法效率高.表2为改进算法与现有算法在处理不同规模的点云数据时所用的时间与空间对比.通过表2可以看出,改进算法虽然在内存占用上有时稍高于现有算法,但在处理相同规模点云时,改进算法相较于原有算法所用时间有着显著的差别,且当点云规模越大时,所用时间差别越明显.
表1 算法相关数据对比
Tab.1 Comparison in related data from different algorithms

算法点云数量重采样点数面片数误差/%现有算法1755430175543035118640.1087改进算法1755430175384035106940.0145
表2 时间空间对比
Tab.2 Comparison in time and space
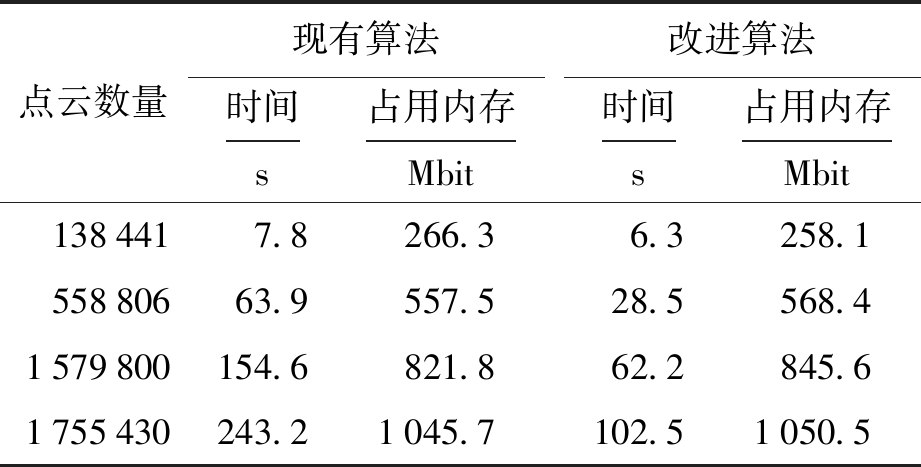
点云数量现有算法时间s占用内存Mbit改进算法时间s占用内存Mbit 138441 7.8266.3 6.3258.155880663.9557.528.5568.41579800154.6821.862.2845.61755430243.21045.7102.51050.5
通过上述实验可以看出,采用本文方法对现有泊松曲面重建算法进行改进后,在噪声点滤除、曲面光滑性与重建效率方面均优于现有泊松曲面重建算法.
4 结 论
本文提出了一种改进的泊松算法并对采集到的车头点云数据进行三维重建.该方法可以使重建的车头模型广顺性更好,减少了异常点对重建精度与效率的影响,省去了最小二乘法的收缩过程,从而提高了重建效率.另外,针对提取等值面时出现的二义性问题,本文采用了一种简化改进方法来解决此问题,提高了重建精度和速度,获得了更加准确的车头模型,为车头测量提供了一种新的方式,也对大尺寸工件的检测起到了推动性的作用.下一步将重点研究如何提高重建精度,以满足更高精度的车头测量要求.
[1]Liu P,Liu D.Filter-based compounded delay estimation with application to strain imaging [J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2011,58(10):2078-2095.
[2]Cheng Y J,Cui S G,Liu D C.Frequency compounding for ultrasound freehand elastography [C]//International Conference on Bioinformatics and Biomedical Engineering (ICBBE) 2010 4th.Chengdu,China,2010:112-117.
[3]Buhmann M D.Radial basis functions [J].Acta Numerica,2000,38(1):25-29.
[4]Hoppe H.Poisson surface reconstruction and its applications [C]//Proceedings of the ACM Symposium on Solid and Physical Modeling.New York,USA,2008:450-457.
[5]Bolitho M,Kazhdan M,Burns R,et al.Parallel poisson surface reconstruction [C]//Advancesin Visual Computing.Berlin,Germany,2009:678-689.
[6]Michael K,Hugues H.Screened poisson surface reconstruction [J].ACM Transactions on Graphics (TOG),2013,32(3):1-13.
[7]刘金玲,唐棣.基于泊松方程实现点云的表面重构 [J].计算机应用与软件,2009,26(4):227-228.
(LIU Jin-ling,TANG Di.The surface reconstruction of point cloud based on poisson equation [J].Computer Application and Software,2009,26(4):227-228.)
[8]朱德海.点云库PCL学习教程 [M].北京:北京航空航天大学出版社,2012:359-361.
(ZHU De-hai.PCL learning tutorial of point cloud library [M].Beijing:Beijing University of Aeronautics and Astronautics Press,2012:359-361.)
[9]Li X L,An T Q,Lu H S,et al.Poisson reconstruction algorithm for scale-varying DEM with features preservation [J].Journal of Lanzhou University of Techno-logy,2014,40(3):135-140.
[10]同济大学数学系.高等数学 [M].北京:高等教育出版社,2007:101-106.
(Mathematics Department of Tongji University.Advanced mathematics [M].Beijing:Higher Education Press,2007:101-106.)
[11]Antonin C,Thomas P.A first-order primal-dual algorithm for convex problems with applications to imaging [J].Journal of Mathematics,2010,40(1):120-145.
[12]杨品林.彩色图像数据库中目标特征数据挖掘方法 [J].沈阳工业大学学报,2018,40(1):60-64.
(YANG Pin-lin.Mining method for target feature data in color image database [J].Journal of Shenyang University of Technology,2018,40(1):60-64.)