聚类是将物理或者抽象的对象集合分成若干个类,使得同一个类中的对象具有较高相似度,不同类中的对象具有较低相似度[1],聚类分析技术在图像处理、模式识别、生物学等诸多领域有着广泛的应用[2-4].在实际生活中的各个方面比如医疗卫生教育、社交网站、商场和购物网站等领域每时每刻都会产生大量的数据,这些数据大多是由连续的数值属性和代表类别的分类属性所构成的混合属性数据,所以混合属性数据聚类算法的研究成为聚类分析领域的一个热点问题.目前,许多学者对混合属性数据聚类进行研究,并提出了一些相关算法.Huang结合k-means和k-modes算法的思想提出了k-prototypes算法[5],该算法实现简单,易操作,能够有效聚类混合数据,但其对初始聚类中心和聚类数目过于依赖,使得聚类结果容易陷入局部最优,并且在计算分类属性之间的相异度时,简单采用数值0和1不能客观地体现数据对象与类之间的相异度,从而导致聚类结果不理想.针对k-prototypes算法存在的问题,欧阳浩等提出了基于信息熵的粗糙k-prototypes聚类算法[6],利用信息熵的概念,为每个数据对象的分类属性赋予权重,并且引入粗糙集的理论来计算各数据对象与粗糙中心之间的差异度,提高了聚类结果的准确率.Chatzis提出了一种新的FCM算法[7],对Gath-Geva算法进行了扩展,该算法假设簇中的数据对象符合高斯分布,主要对高斯多项分布数据进行聚类.Zheng等利用进化算法(EA)具有全局搜索能力的特点,将其引入到k-prototypes算法中,提出EKP算法[8],算法中令k-prototypes算法作为局部搜索策略,并在EA框架的控制下运行.钱潮恺等[9]针对k-prototypes算法分辨率低,聚类结果的随机性较大等问题,提出基于维度频率相异度的方法来计算分类属性,并且对预聚类产生的子簇构造连通图,分析其之间的连通关系,用强连通融合方法进行聚类.陈晋音等提出了基于混合属性距离度量公式的密度聚类算法[10],将数据对象分为分类占优、数值占优和均衡型,对于不同情况的特征,分别选择不同的距离度量方式,通过预先设定的参数寻找数据密度最大的区域,选定核心点,再根据核心点将密度相连的数据对象划分为一类,最后得到聚类结果.
上述处理混合属性数据的算法虽然在不同程度上提高了聚类效果,但大都采取了随机选择初始聚类中心的方式,给算法的执行效率带来了很大的不确定性[11].为了解决这个问题,已有学者提出一些改进算法,文献[12]在考虑数据对象在类归属上不确定的同时,利用均值和分布质心表示类中心;文献[13]提出了基于密度聚类中心自动确定的聚类算法.实际上,聚类中心点的分布比较疏散,不会局限在一个小的范围区域内.本文利用平均差异度方法选取初始聚类中心点,并用这些点进行聚类,可以得到较好的效果.为进一步提高算法质量,利用信息熵确定数值属性权重,并对分类属性度量公式进行改进,给出了一种混合属性数据度量公式.
1 k-prototypes聚类算法
k-prototypes算法能够聚类由数值属性和分类属性组成的混合数据集,该算法将k-means算法与k-modes算法相结合,在聚类过程中引入参数γ来控制分类属性数据对聚类结果的影响程度.设X={x1,x2,,xn}表示由n个数据对象组成的数据集,其中xi(1≤i≤n)具有m个属性A1,A2,,Ap,Ap+1,,Am,其中,A1,A2,,Ap为数值属性,Ap+1,Ap+2,,Am为分类属性,用Dom(Aj)来表示属性Aj的值域,数值属性值域用连续值表示,分类属性值域用有限的、无任何自然顺序的集合表示,如颜色、血型、性别等,通常用Dom(Aj)=![]() 来表示,其中nj为属性Aj的数目.数据集中对象xi∈X可以用m维向量来表示,即xi={xi1,xi2,,xip,xi(p+1),,xim},其中xij∈Dom(Aj).
来表示,其中nj为属性Aj的数目.数据集中对象xi∈X可以用m维向量来表示,即xi={xi1,xi2,,xip,xi(p+1),,xim},其中xij∈Dom(Aj).
设k∈N+,k-prototypes算法聚类是将数据集划分成k个不同的类,使得目标函数值最小,即
(1)
式中:vl为类cl的聚类中心,cl为聚类集;μil为数据对象xi对类cl的隶属度,0≤μil≤1;d(xi,vl)为混合属性数据度量公式,即
(2)
其中:![]() 为类中分类属性的权重;当xij为数值属性时,vlj为类cl中第j个数值属性的平均值;当xij为分类属性时,vlj为类cl中第j个分类属性中出现概率最大的值.k-prototypes算法的流程如下:
为类中分类属性的权重;当xij为数值属性时,vlj为类cl中第j个数值属性的平均值;当xij为分类属性时,vlj为类cl中第j个分类属性中出现概率最大的值.k-prototypes算法的流程如下:
1) 在数据集中任选k个初始聚类中心点;
2) 根据式(2)计算对象与初始聚类中心的距离,按照最小距离原则分到离其最近的中心所在的类中;
3) 更新聚类中心,对数值属性数据求平均值,对分类属性数据求属性中出现次数最多的值;
4) 重复步骤2)和3),直到目标函数F不再发生变化为止.
2 改进k-prototypes聚类算法
k-prototypes算法虽实现了混合属性数据的有效聚类,但在聚类过程中仍存在一些问题,随机选取初始聚类中心导致聚类结果具有不确定性和随机性.采用式(2)计算数据对象间的相似度,忽略了数值属性数据对聚类结果的影响.同时分类属性采用简单匹配度量计算数据与类中心的相似度有两个缺点:1)不能准确地描述数据对象与类中心对应的簇中其他数据的相似度,数据对象是否被划分到一个簇中,不仅依赖于与聚类中心的相似度,还依赖于与类内已有对象的总体相似度;2)当数据对象与多个聚类中心的相似度相同时,算法往往会随机将此数据加入到一个聚类集中,从而不能准确地划分到相似性更大的聚类集中.
2.1 改进的混合属性数据度量公式
针对k-prototypes算法存在的问题,利用信息熵Ej的概念对数值属性进行加权,并对分类属性度量公式进行改进,给出混合属性数据度量公式.
对于数据对象X={x1,x2,,xn},xi具有p个数值属性,![]() 表示数据对象xi的第j维属性值比重,xij为属性值,则第j维属性的信息熵为
表示数据对象xi的第j维属性值比重,xij为属性值,则第j维属性的信息熵为
(3)
权值表示为![]() 其中
其中![]() 1,0≤ωij≤1.基于信息熵加权的数值属性距离度量公式如定义1所示.
1,0≤ωij≤1.基于信息熵加权的数值属性距离度量公式如定义1所示.
定义1 数值属性度量采用加权曼哈顿距离公式,数据对象xi与xj之间的度量计算定义为
(4)
由于数值属性的取值范围不同,在进行聚类之前需要消除属性之间的量纲,利用文献[14]中的公式![]() 对数值属性数据进行标准化处理.
对数值属性数据进行标准化处理.
定义2 设cl表示聚类过程中的一个类,则分类属性度量公式定义为
(5)
式中:![]() 为分类属性数据到聚类集cl的距离;clsj为类cl中第s个数据对象的第j个属性值;|cl|为类cl中已有数据对象的个数.利用定义1和定义2确定混合属性数据度量公式.
为分类属性数据到聚类集cl的距离;clsj为类cl中第s个数据对象的第j个属性值;|cl|为类cl中已有数据对象的个数.利用定义1和定义2确定混合属性数据度量公式.
定义3 设cl为聚类过程中的一个类,![]() 表示聚类中心,其中
表示聚类中心,其中![]() 为数值属性数据的平均值,
为数值属性数据的平均值,![]() 为分类属性部分各属性值中出现次数最多的值,则混合属性数据度量公式为
为分类属性部分各属性值中出现次数最多的值,则混合属性数据度量公式为
(6)
将定义3应用到k-prototypes算法的目标函数中,即
(7)
2.2 初始聚类中心选取
为了克服随机选择初始聚类中心导致聚类结果不稳定的问题,借鉴文献[15]中选择初始聚类中心点的思想,并且利用平均差异度选取初始聚类中心.基于的原则是:初始聚类中心应具有较大的平均差异度,且聚类中心之间的差异度要大于总体平均差异度.
对于任意一个数据对象xi,需要计算两个量,即每个数据对象的平均差异度![]() 和数据对象的总体平均差异度
和数据对象的总体平均差异度![]()
平均差异度的计算依赖于数据对象两两之间的距离d(xi,xj),本文采用混合属性数据距离代替原方法中的欧式距离,其中数值部分为由定义1给出的数值属性度量公式,分类属性部分采用简单匹配度量,从而扩展了原方法只能处理数值属性数据的限制,使其能够更好地解决混合属性数据聚类问题.
2.3 算法描述
综上得到基于平均差异度的改进k-prototypes聚类算法的步骤如下:
1) 给定聚类个数k,计算每个数据对象的平均差异度和总体平均差异度,将平均差异度进行排序,并把平均差异度最大的数据对象作为第1个初始聚类中心v1,同时将该数据从数据集中删除;
2) 寻找其余数据对象中平均差异度最大的数据,计算其与已有聚类中心的距离;
3) 若计算其与已有聚类中心的距离均不小于总体平均差异度,则可作为聚类中心,否则,返回步骤2),重复步骤2)和3),直到初始聚类中心的个数达到k,并输出初始聚类中心;
4) 根据定义3计算数据对象到各聚类集的距离,按照就近原则将数据分配到离其最近的聚类集中;
5) 更新每个类的中心,对数值属性数据计算平均值,对分类属性数据取属性中出现概率最大的值;
6) 重复步骤4)和5),直到各个聚类中心稳定,目标函数值不再发生变化,结束.
3 仿真试验与结果分析
3.1 试验环境
本文仿真试验采用Matlab R2012a开发环境,Intel(R) Core(TM) i3-4005U CPU 1.70 GHz,4 GB内存,在Windows7操作系统上运行.试验数据采用UCI机器学习数据库中的4个真实数据集,数据集描述如表1所示.
表1 试验数据集描述
Tab.1 Description of experiment data sets

数据集数据量数值属性数分类属性数类别数Iris150403Soybean470354Credit690682Heart270582
以上4个数据集包括3种数据类型,其中Iris为数值型数据,Soybean为分类型数据,Credit和Heart为混合型数据.
为了评估聚类质量,采用文献[10]中的公式![]() 作为评价标准,其中,ai为每个聚类被正确分类的数据对象个数,k为聚类个数,n为数据集的总数.按照该评价指标,r取值越大,得到的聚类结果越理想.
作为评价标准,其中,ai为每个聚类被正确分类的数据对象个数,k为聚类个数,n为数据集的总数.按照该评价指标,r取值越大,得到的聚类结果越理想.
3.2 试验结果
为了验证本文算法的有效性和可行性,分别用k-prototypes算法、EKP算法、KL-FCM-GM算法、文献[12]算法、文献[13]算法和本文算法对上述数据进行聚类分析,试验结果如图1所示.
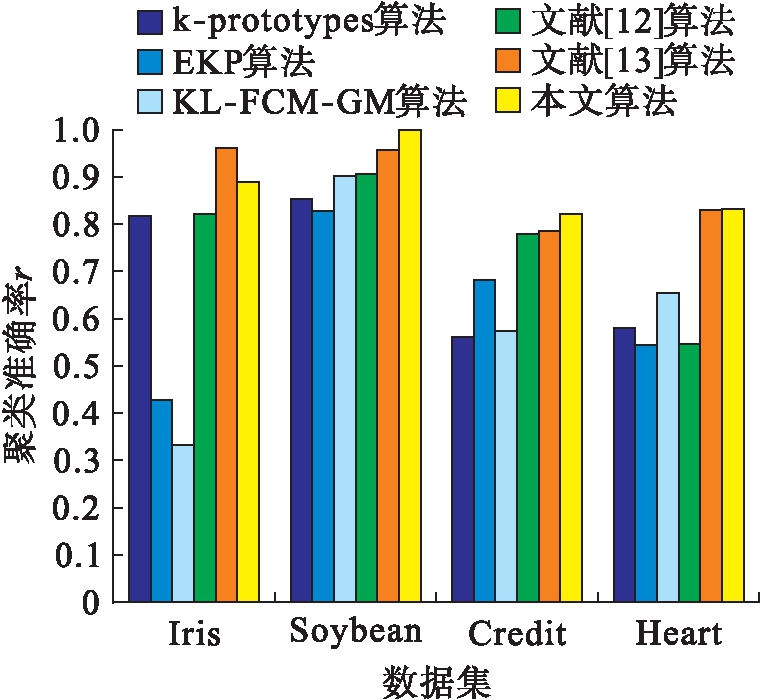
图1 各种算法的聚类准确率
Fig.1 Clustering accuracy of various algorithms
从图1可以看出,本文算法在处理Soybean数据集、Credit数据集和Heart数据集时,聚类准确率都高于其他算法,只有在处理Iris数据时,低于文献[13]算法,但优于其他算法.这说明本文算法在处理混合型数据和分类型数据时有效性更高,而处理数值型数据有待提高.
为了进一步验证本文算法的聚类质量,比较本文算法与k-prototypes算法的聚类精度,利用Credit数据集的聚类结果,根据数据集依次迭代不同次数所对应的目标函数值,生成的对比结果如图2所示.
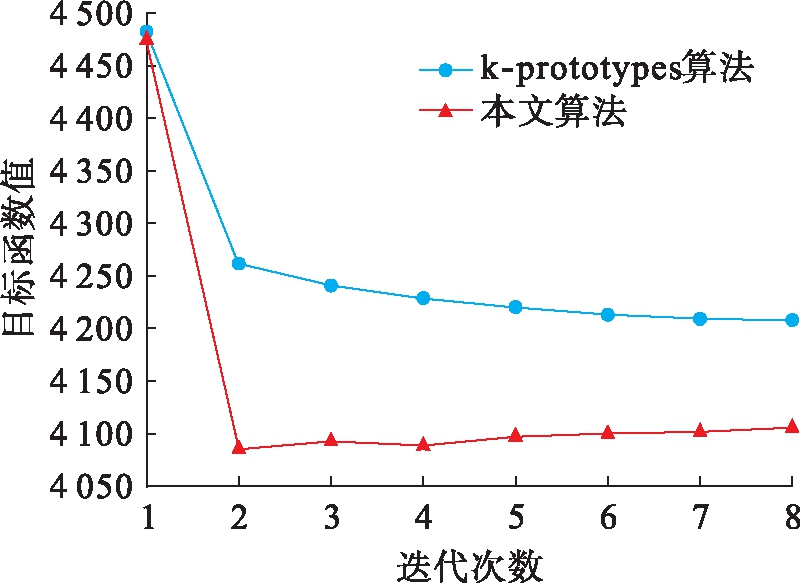
图2 迭代次数与目标函数曲线
Fig.2 Curves of iteration number and objective function
从图2可以看出,目标函数值均随着迭代次数的增高而降低,但是在相同条件下,本文算法的目标函数值比k-prototypes算法低,说明本文算法的聚类精度比k-prototypes算法高.
3.3 算法复杂度分析
本文算法主要由初始聚类中心的选取和聚类迭代两部分构成,其中选取初始聚类中心要计算数据对象之间的距离和寻找聚类中心,该过程的计算代价分别为O(n2)和O(kn),确定聚类中心后,算法需要进行迭代划分,其计算代价为O(tkn),因此,总的时间复杂度变为O(n2+kn+tkn),其中,t为迭代次数,k≪n.本文算法和其他算法的时间复杂度比较如表2所示.
表2 算法的时间复杂度统计
Tab.2 Statistics results of time complexity for various algorithms

算法时间复杂度k-prototypesO((t+1)kn)EKPO(nkt)KL-FCM-GMO(t(dlk+n(c+2)))文献[12]O(k(m+p+Nm-Np)nl)文献[13]O(n2+(n2-n)/2+n-k)本文算法O(n2+kn+tkn)
从表2中分析可以得出,本文算法的时间复杂度比k-prototypes、EKP、KL-FCM-GM及文献[12]要高,主要消耗在选取初始聚类中心的环节上,但是确定了较优的聚类中心点之后,会减少迭代次数,并得到较满意的聚类结果,从而在一定程度上可以弥补时间复杂度较高的不足.
4 结 论
本文提出的基于平均差异度的改进k-prototypes聚类算法,是在传统k-prototypes聚类算法基础上进行的扩展.通过利用平均差异度确定初始聚类中心,考虑了数据的空间分布信息,使得聚类中心更符合实际情况,避免了对初始中心选择所带来的不确定性.改进的分类属性数据度量公式,不仅考虑了数据对象与类中心的距离,还有效利用了数据与类中已有对象之间的总体相异性,使得在迭代过程中,对聚类集中已有对象的信息进行了统计参考,从而获得更好的聚类结果.但该算法中聚类数目的选择会影响聚类结果,因此,下一步将研究聚类数目的确定方法,寻找能够自动选取合理聚类数目的方法.
[1]Han J W,Kamber M.Data mining concepts and techniques [M].Beijing:Mechanical Industry Press,2014.
[2]杨品林.彩色图像数据库中目标特征数据挖掘方法 [J].沈阳工业大学学报,2018,40(1):60-64.
(YANG Pin-lin.Mining method for target feature data in color image database [J].Journal of Shenyang University of Technology,2018,40(1):60-64.)
[3]Bishnu P S,Bhattacherjee V.Software fault prediction using quad tree-based K-means clustering algorithm [J].IEEE Transactions on Knowledge & Data Engineering,2012,24(6):1146-1150.
[4]Oyelade J,Isewon I,Oladipupo F,et al.Clustering algorithms:their application to gene expression data [J].Bioinformatics & Biology Insights,2016,10:237-253.
[5]Huang Z X.Clustering large data sets with mixed numeric and categorical values [C]//The First Pacific Asia Conference on Knowledge Discovery and Data Mining.Singapore,Singapore,1997:21-34.
[6]欧阳浩,戴喜生,王智文,等.基于信息熵的粗糙K-prototypes聚类算法 [J].计算机工程与设计,2015,36(5):1239-1243.
(OUYANG Hao,DAI Xi-sheng,WANG Zhi-wen,et al.Rough K-prototypes clustering algorithm based on entropy [J].Computer Engineering and Design,2015,36(5):1239-1243.)
[7]Chatzis S P.A fuzzy c-means-type algorithm for clustering of data with mixed numeric and categorical attributes employing a probabilistic dissimilarity functional [J].Expert Systems with Applications,2011,38(7):8684-8689.
[8]Zheng Z,Gong M G,Ma J J,et al.Unsupervised evolutionary clustering algorithm for mixed type data [C]//Proceedings of the IEEE Congress on Evolutionary Computation (CEC).Barcelona,Spain,2010:1-8.
[9]钱潮恺,黄德才.基于维度频率相异度和强连通融合的混合数据聚类算法 [J].模式识别与人工智能,2016,29(1):82-89.
(QIAN Chao-kai,HUANG De-cai.Clustering algorithm for mixed data based on dimensional frequency dissimilarity and strongly connected fusion [J].Pattern Recognition and Artificial Intelligence,2016,29(1):82-89.)
[10]陈晋音,何辉豪.基于密度和混合距离度量方法的混合属性数据聚类研究 [J].控制理论与应用,2015,32(8):993-1002.
(CHEN Jin-yin,HE Hui-hao.Density-based clustering algorithm for numerical and categorical data with mixed distance measure methods [J].Control Theory & Applications,2015,32(8):993-1002.)
[11]庞天杰,赵兴旺.一种基于先验信息的混合数据聚类个数确定算法 [J].计算机科学,2016,43(2):101-104.
(PANG Tian-jie,ZHAO Xing-wang.Algorithm to determine number of clusters for mixed data based on prior information [J].Computer Science,2016,43(2):101-104.)
[12]Ji J C,Bai T,Zhou C G,et al.An improved K-prototypes clustering algorithm for mixed numeric and categorical data [J].Neurocomputing,2013,120:590-596.
[13]Chen J Y,He H H.A fast density-based data stream clustering algorithm with cluster centers self-determined for mixed data [J].Information Sciences,2016,345:271-293.
[14]常茜茜,张月琴.一种基于划分的混合数据聚类算法 [J].计算机应用与软件,2014,31(6):154-157.
(CHANG Xi-xi,ZHANG Yue-qin.A partition-based clustering algorithm for mixed data [J].Computer Applications and Software,2014,31(6):154-157.)
[15]李武,赵娇燕,严太山.基于平均差异度优选初始聚类中心的改进K-均值聚类算法 [J].控制与决策,2017,32(4):759-762.
(LI Wu,ZHAO Jiao-yan,YAN Tai-shan.Improved K-means clustering algorithm optimizing initial clustering centers based on average difference degree [J].Control and Decision,2017,32(4):759-762.)