脉冲信号检测在目标探测、定位、跟踪、识别中起着不可替代的作用,尤其是对未知脉冲信号检测[1-4]方面.对未知脉冲信号检测常用的方法有瞬时频率方差法[5-8]和能量累积法[9-12]等,而瞬时频率方差法实现对未知脉冲信号检测的基础为瞬时频率估计.为了提高瞬时频率方差法对未知脉冲信号瞬时频率的估计精度,本文提出了一种瞬时频率高精度估计方法.该方法采用快速傅里叶变换(FFT)与陷波滤波器相结合,实现对未知脉冲信号瞬时频率高精度估计.首先利用FFT分析实现对信号频率粗略估计,然后采用多次迭代陷波滤波器提高对信号瞬时频率的估计精度,最后对估计偏差进行修正,保证频率估计的无偏性.本文需设置陷波滤波器迭代次数,可通过瞬时频率估计差值进行判断设置.同时,为了提高对未知脉冲检测的鲁棒性和普适性,在未知脉冲信号检测中,本文提出一种基于瞬时频率高精度估计的联合检测方法.
理论分析和实验结果表明,一定信噪比条件下,该方法可以实现对未知脉冲信号瞬时频率的高精度估计,估计方差接近克拉美罗下界(Cramer-Rao lower bound,CRLB).同时,由于本文在对未知脉冲检测过程中,综合了瞬时频率方差检测器和能量累积检测器的优势,可有效克服瞬时频率方差检测器对宽带脉冲信号检测的不足和能量累积检测器对窄带脉冲信号检测的不足,突破常规检测方法采用单一方式对未知脉冲信号实现检测所存在的弊端,提高对未知脉冲检测的鲁棒性和普适性,为未知脉冲检测与瞬时频率高精度估计在实际中的应用提供了一个新思路.
1 高精度频率估计方法
陷波滤波器常用于对已知信号瞬时频率和相位的高精度估计.对于未知脉冲信号瞬时频率估计需要借助其他信息处理得到频率估计初始值,否则可能得不到收敛的瞬时频率估计结果.因此,本文提出一种未知脉冲信号瞬时频率高精度估计方法.
1.1 算法原理
为了便于分析,文中阵元采集数据用x(t)表示,即x(t)=s(t)+n(t),数据长度为L.其中,s(t)=Acos(2πfct+φ0)为单频信号,A为单频信号幅度,φ0为初相位,两者均为常量,fc为频率估计值;n(t)为宽带噪声;xc(t)和xs(t)为两路正交参考输入;wc(t)和ws(t)为权值输出;ε(t)为残差输出;y(t)为信号输出.
本文所述未知信号瞬时频率高精度估计方法可通过以下几个步骤实现:
1) 对采集信号阵元采集数据x(t)进行FFT分析,得到频率估计初始值f0,并将初始值赋予单频信号载频估计值fc=f0.
2) 采用陷波滤波器实现高精度瞬时频率估计.令两路正交参考输入为
(1)
式中,A1为参考信号的幅度.设自适应学习步长为常量μ,采用LMS算法,递推公式为
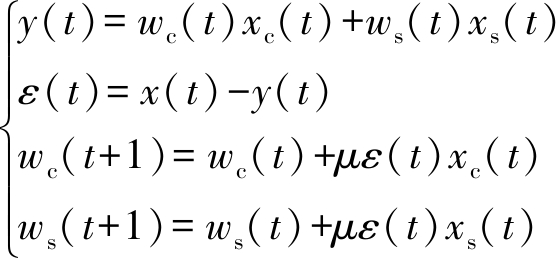
(2)
根据得到的输出信号y(t),可得到输出信号相位,瞬时频率前后差值Δf(t),瞬时频率值,以及本次输出信号和误差信噪比SNRout(m),即
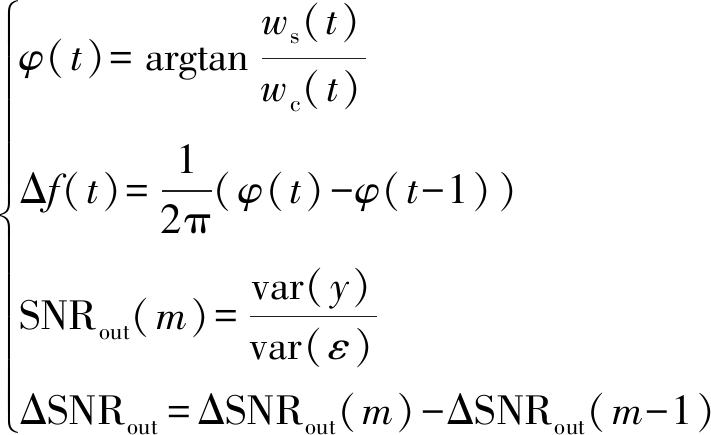
(3)
式中,var()为估计精度.若信号频率稳定,可以取瞬时频率的平均值为信号载频的估计值.
3) 根据步骤2)所得结果,利用瞬时频率前后差值Δf(t)可得均值![]() 即
即
(4)
4) 将步骤2)、3)所得信息与所设置的门限值α、β进行比较,若![]() 或ΔSNRout≤β,可得信号载频为
或ΔSNRout≤β,可得信号载频为![]() 否则设置计数器m=m+1,判断当前计数器值是否达到所设定值M,若m>M,可得信号载频为
否则设置计数器m=m+1,判断当前计数器值是否达到所设定值M,若m>M,可得信号载频为![]() 否则,令
否则,令![]() 并重复执行步骤2)~4).
并重复执行步骤2)~4).
1.2 性能分析
由上述方法可知,该方法等同于相位差分频率估计器,文献[1]已对其性能进行了详细描述,在一定信噪比下,该方法为近似无偏估计,其估计精度为
(5)
式中:T为采样点数;P为功率信噪比;ρ为数据样本首尾噪声的相关系数,对于白噪声则有ρ=0.而频率估计的CRLB为
(6)
在一定信噪比下,相位差分频率估计器的测频方差与CRLB之比为
(7)
2 未知脉冲检测方法
在平稳高斯白噪声背景下检测窄带脉冲信号时,瞬时频率序列方差检测器的性能接近于最佳检测器——匹配滤波器(或相关器).在非平稳干扰背景下,瞬时频率方差检测器的性能稳定,检测能力优于各种常规检测器,如匹配滤波器、相关器、能量检测器,且对多普勒频移引起的失配不敏感.瞬时频率方差检测器与能量检测器结合起来构成的联合检测器可以显著改善在干扰背景中对窄带脉冲的检测能力.因此,为了提高对未知脉冲检测的鲁棒性和普适性,在未知脉冲信号检测中,本文提出一种基于瞬时频率高精度估计的联合检测方法.图1为未知脉冲信号检测流程图.
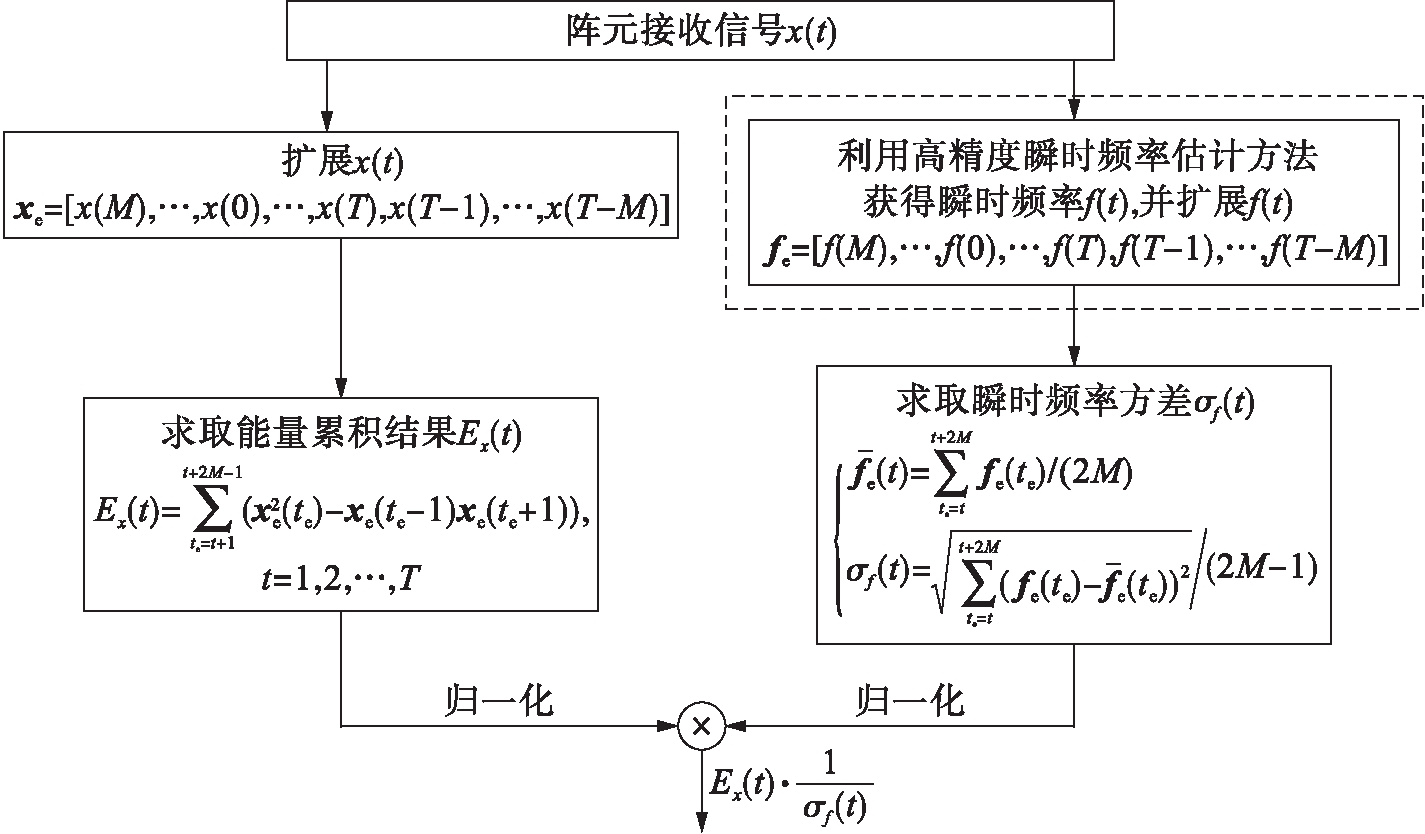
图1 未知脉冲信号检测流程图
Fig.1 Flow chart of unknown pulse signal detection
2.1 瞬时频率方差法
根据未知信号瞬时频率高精度估计方法可得信号瞬时频率f(t),为了充分利用信号瞬时频率信息,文献[1]分析了信号瞬时频率二阶矩特性,并将其应用于窄带信号脉冲检测中.本文为了利用瞬时频率二阶矩信息,首先对信号瞬时频率进行扩展,即
fe=[f(M),,f(0),,f(T),
f(T-1),,f(T-M)]
(8)
式中,2M为计算瞬时频率二阶矩所需数据长度.采用式(9)可得信号瞬时频率方差,即
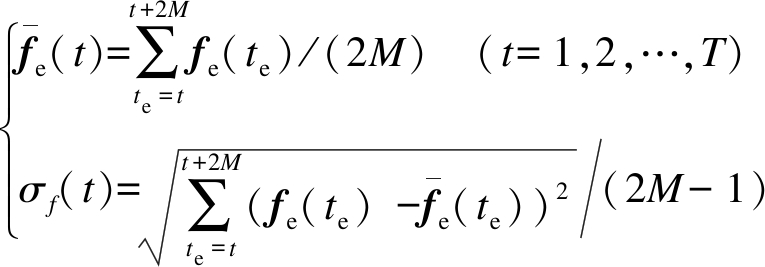
(9)
2.2 能量累积法
能量累积是从高斯背景噪声中检测宽带信号的最佳检测器.首先对阵元采集信号进行扩展,可得
xe=[x(M),,x(0),,x(T),
x(T-1),,x(T-M)]
(10)
式中,2M-1为计算能量累积所需数据长度.根据式(11)可得信号能量累积,即
![]()
(t=1,2,,T)
(11)
2.3 本文方法
为了提高不同方法对未知脉冲信号检测的鲁棒性和普适性,本文将能量累积法和瞬时频率方差法相结合,依据不同方法在信号检测中适应范围的不同,可进一步提高本文方法在未知脉冲信号检测中的鲁棒性.新的检测统计量可表示为
(12)
式中:σf(t)为瞬时频率方差检测器所得瞬时频率方差(已归一化);Ex(t)为能量累积检测器所得能量累积结果(已归一化).
1) 窄带脉冲信号.当脉冲信号中只存在窄带信号时,如果采用能量累积法对其实现检测,则脉冲处累积幅度增益为
(13)
而本文方法所得脉冲处累积幅度增益为
(14)
由此可知,在一定信噪比下,本文方法在脉冲处累积幅度增益远大于能量累积法.
2) 宽带脉冲信号.当脉冲信号为宽带信号时,如果采用瞬时频率方差法对其实现检测,则脉冲处累积幅度增益为
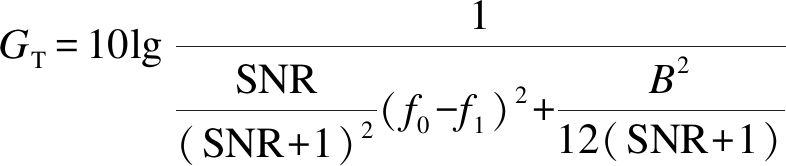
(15)
式中:B为参考信号的幅度;f1为幅度为B的参考信号的频率.而本文方法所得脉冲处累积幅度增益为
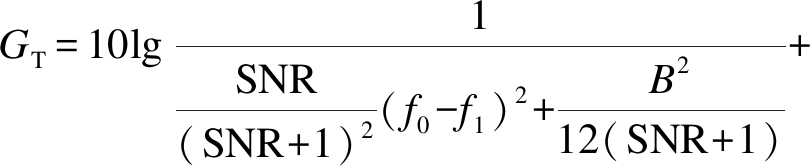
(16)
由此可知,在一定信噪比下,本文方法在脉冲处累积幅度增益远大于瞬时频率方差法.该方法综合了两种方法的优势,克服了瞬时频率方差检测器对宽带脉冲信号检测的不足和能量累积检测器对窄带脉冲信号检测的不足,突破了常规检测方法采用单一方式对窄带或宽带未知脉冲信号实现检测所存在的弊端,提高了对未知脉冲检测的鲁棒性和普适性,可对窄带或宽带未知脉冲信号实现有效检测.
3 数值仿真分析
3.1 高精度瞬时频率估计
MATLAB数值仿真条件为:单频信号中心频率fc=999.856 Hz,背景噪声带宽f=100~500 Hz,系统采样频率fs=20 kHz,样本长度L=1 s,单频信号与背景噪声信噪比为SNR.图2为FFT分析法(一次FFT分析点数为16 384)和本文方法所得瞬时频率估计结果,每次估计结果是由500次蒙特卡罗统计平均所得,μ=0.025.
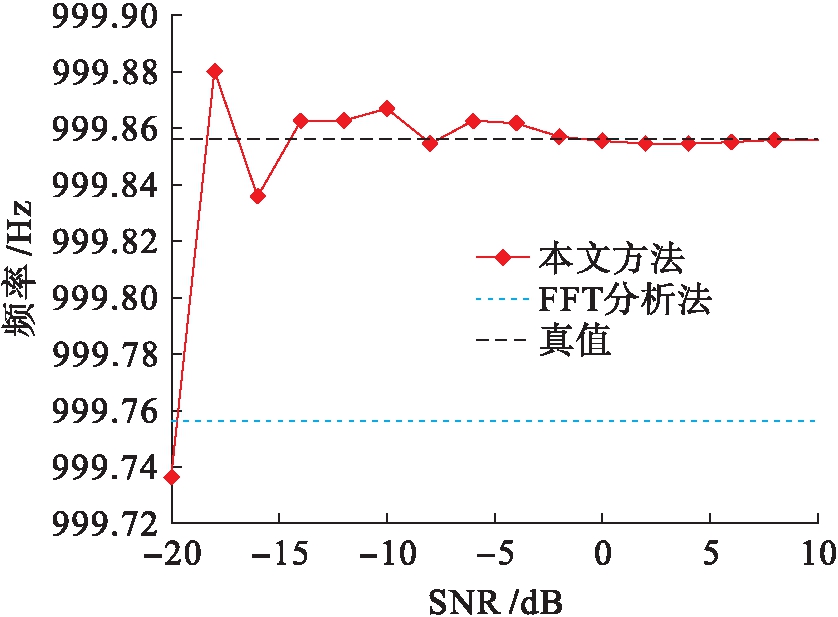
图2 不同方法所得频率估计结果
Fig.2 Frequency estimation results obtained with different methods
由图2可知,本文方法在一定信噪比条件下,瞬时频率估计结果相比FFT分析法更接近于真值,具有较高的频率估计精度,瞬时频率估计方差更接近克拉美罗下界,估计精度提高了0.1%,数值仿真结果与理论分析相符合.
3.2 窄带未知脉冲检测
MATLAB数值仿真条件为:窄带脉冲信号中心频率fc=159.856 Hz,脉冲长度为0.1 s,占空比为10%,背景噪声带宽f=100~500 Hz,系统采样频率fs=20 kHz,样本长度L=1 s,窄带脉冲信号与背景噪声信噪比SNR=-12 dB.图3为窄带脉冲信号时频域波形.图4为瞬时频率方差法、能量累积法和本文方法对窄带未知脉冲所得检测结果.
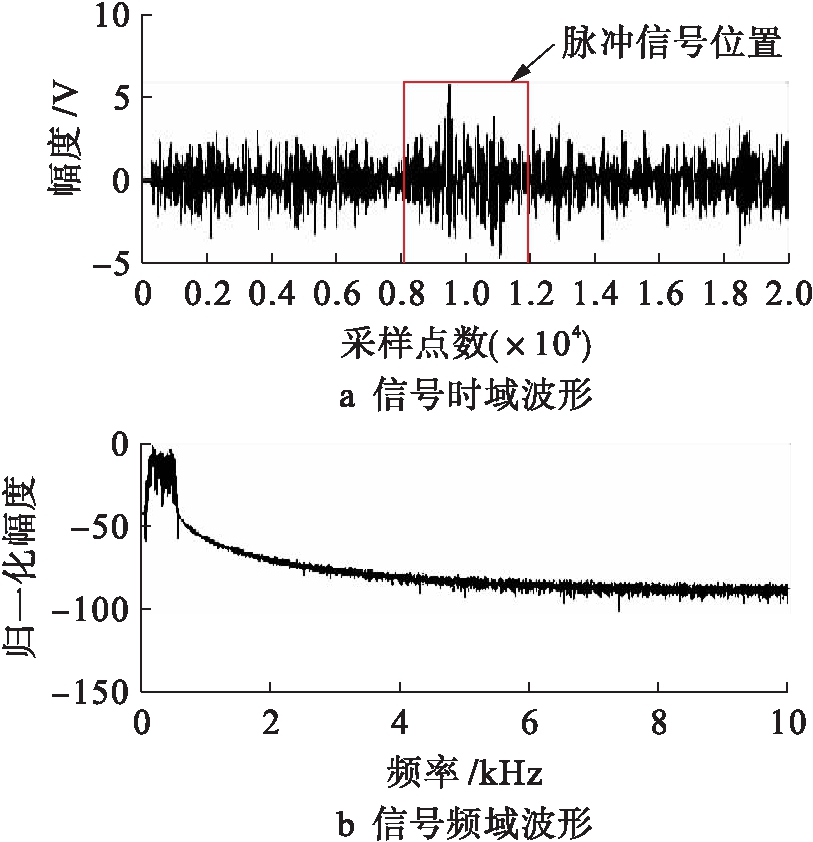
图3 窄带脉冲信号时频域波形
Fig.3 Time-frequency domain waveform of narrow band pulse signal
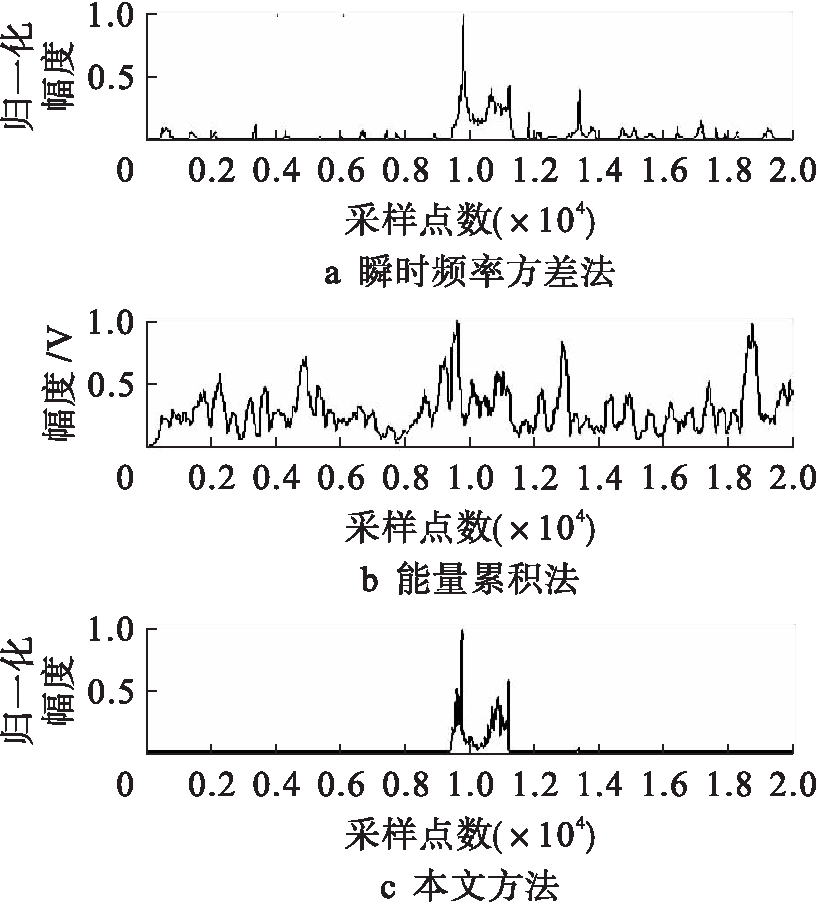
图4 不同方法所得窄带未知脉冲检测结果
Fig.4 Detection results of narrow band unknownpulse obtained with different methods
3.3 宽带未知脉冲检测
MATLAB数值仿真条件为:脉冲信号为宽带信号,脉冲长度为0.1 s,占空比为10%,脉冲信号与背景噪声带宽f=100~500 Hz,系统采样频率fs=20 kHz,样本长度L=1 s,脉冲信号与背景噪声信噪比SNR=5 dB.图5为宽带脉冲信号时频域波形.图6为瞬时频率方差法、能量累积法和本文方法对宽带未知脉冲所得检测结果.
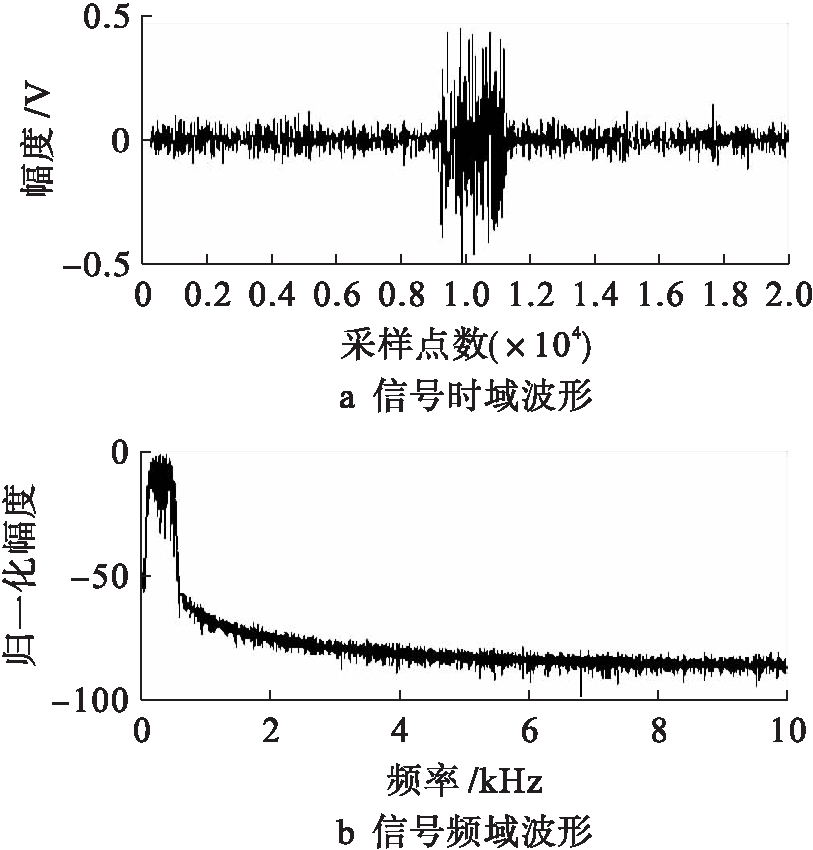
图5 宽带脉冲信号时频域波形
Fig.5 Time-frequency domain waveform of broad band pulse signal
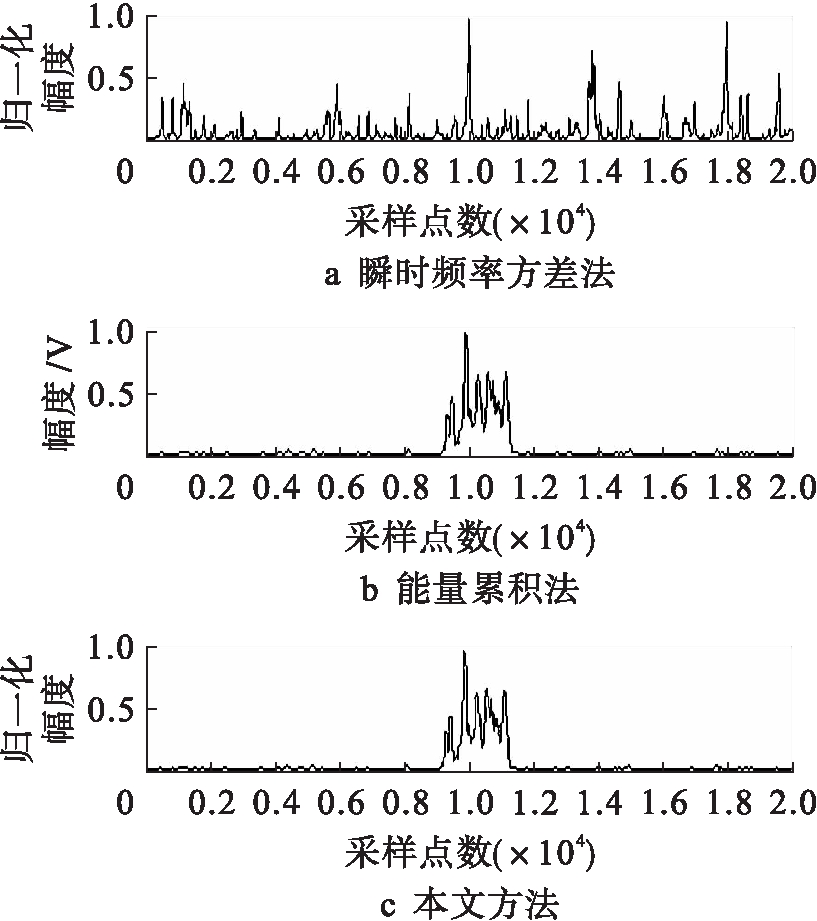
图6 不同方法所得宽带未知脉冲检测结果
Fig.6 Detection results of broad band unknown pulse obtained with different methods
由图4、6可知,在一定信噪比条件下,当脉冲信号为窄带信号时,采用瞬时频率方差法和本文方法可以对未知脉冲实现有效检测,而采用能量累积法并不能对窄带未知脉冲实现有效检测;当脉冲信号为宽带信号时,采用能量累积法和本文方法可以对宽带未知脉冲实现有效检测,而采用瞬时频率方差法并不能对宽带未知脉冲实现有效检测.而本文方法在两种情况下,均可对未知脉冲信号实现有效检测,可知本文方法的鲁棒性和普适性最好,数值仿真结果符合理论分析.
4 结 论
针对未知脉冲信号检测与瞬时频率估计问题,本文提出了一种瞬时频率高精度估计方法.该方法采用快速傅里叶变换(FFT)分析与陷波滤波器相结合,实现了对未知信号瞬时频率高精度估计.理论分析和实验结果表明,在一定信噪比条件下,本文方法可以实现对未知信号瞬时频率的高精度估计,瞬时频率估计方差接近克拉美罗下界,估计精度提高了0.1%.
同时,为了提高对未知脉冲检测的鲁棒性和普适性,在未知脉冲信号检测中,本文提出一种基于瞬时频率高精度估计的联合检测方法.对比图4、6结果可知,该方法可实现对窄带或宽带未知脉冲信号的有效检测,克服了瞬时频率方差检测器对宽带脉冲信号检测的不足和能量累积检测器对窄带脉冲信号检测的不足,即该方法突破了常规检测方法采用单一方式对窄带或宽带未知脉冲信号实现检测所存在的弊端,提高对窄带或宽带未知脉冲检测的鲁棒性和普适性,为未知脉冲检测与瞬时频率高精度估计在实际中的应用提供了一个新思路.
[1]梁国龙,杨春,王德俊.频点自跟踪自适应频率估计器性能研究 [J].电子学报,2005,33(7):1204-1208.
(LIANG Guo-long,YANG Chun,WANG De-jun.Research on properties of frequency auto-tracking adaptive frequency estimator [J].ACTA Electronica Sinica,2005,33(7):1204-1208.)
[2]王燕,邹男,付进,等.基于局部瞬时能量密度级的瞬态信号检测方法 [J].电子与信息学报,2013,35(7):1720-1724.
(WANG Yan,ZOU Nan,FU Jin,et al.Transient signal detection method based on partial instantaneous energy density level [J].Journal of Electronics & Information Technology,2013,35(7):1720-1724.)
[3]陈川,陈韶华,李琪.基于自适应 Notch 滤波器的矢量阵多目标分辨研究 [J].兵工学报,2011,32(9):1131-1135.
(CHEN Chuan,CHEN Shao-hua,LI Qi.Multi-sources distinguishing with acoustic vector sensor array based on adaptive Notch filter [J].ACTA Armamentarii,2011,32(9):1131-1135.)
[4]付彦,刘劲军.一种基于Notch 滤波器的恒定束宽波束形成技术 [J].声学技术,2013,32(1):50-53.
(FU Yan,LIU Jin-jun.Constant beamwidth beamforming based on adaptive filter [J].Technical Acoustics,2013,32(1):50-53.)
[5]郑恩明,陈新华,孙长瑜.基于频率方差加权的时延差估计方法 [J].系统工程与电子技术,2014,36(2):224-229.
(ZHENG En-ming,CHEN Xin-hua,SUN Chang-yu.Time delay difference estimation weighted method based on frequency variance [J].Systems Engineering and Electronics,2014,36(2):224-229.)
[6]梁国龙,惠俊英.瞬时频率方差检测器(VIFD)及其性能评价 [J].声学学报,1999,24(2):183-190.
(LIANG Guo-long,HUI Jun-ying.Variance-of-instantaneous-frequency detector and its performance evaluation [J].ACTA Acustica,1999,24(2):183-190.
[7]魏振坤,冯海泓,黄敏燕,等.瞬时频率方差检测器的实际性能分析 [J].声学技术,2010,29(5):533-537.
(WEI Zhen-kun,FENG Hai-hong,HUANG Min-yan,et al.Analysis of practical performance of the variance-of-instantaneous-frequency detector [J].Technical Acoustics,2010,29(5):533-537.)
[8]郑恩明,余华兵,陈新华,等.一种基于瞬时相位方差加权的线谱检测器 [J].电子与信息学报,2015,37(7):1763-1768.
(ZHENG En-ming,YU Hua-bing,CHEN Xin-hua,et al.Weighted line spectrum detector based on instantaneous phase variance [J].Journal of Electronics & Information Technology,2015,37(7):1763-1768.)
[9]李启虎,李敏,杨秀庭.水下目标辐射噪声中单频信号分量的检测:理论分析 [J].声学学报,2008,33(3):193-196.
(LI Qi-hu,LI Min,YANG Xiu-ting.The detection of single frequency component of underwater radiated noise of target:theoretical analysis [J].ACTA Acoustica,2008,33(3):193-196.)
[10]郑恩明,陈新华,孙长瑜.基于幅值加权的未知线谱目标检测方法 [J].振动与冲击,2014,33(16):160-165.
(ZHENG En-ming,CHEN Xin-hua,SUN Chang-yu.Unknown target detection method based on weighted amplitude [J].Journal of Vibration and Shock,2014,33(16):160-165.)
[11]郑恩明,孙长瑜,陈新华.基于主副瓣比加权的未知线谱目标检测方法研究 [J].应用声学,2015,34(4):311-319.
(ZHENG En-ming,SUN Chang-yu,CHEN Xin-hua.Unknown target detection weighted method based on the main side lobe ratio [J].Applied Acoustics,2015,34(4):311-319.)
[12]郑恩明,田甜,陈新华,等.基于波束域相位稳定性的目标检测方法研究 [J].电子学报,2016,44(9):2033-2039.
(ZHENG En-ming,TIAN Tian,CHEN Xin-hua,et al.Target detection method based on the stability of beam domain phase [J].ACTA Electronica Sinica,2016,44(9):2033-2039.)