近年来,优化问题在很多行业越来越受到关注和重视,同时也发挥着重要作用.目前,优化对象变得越来越复杂,传统优化方法在解决这些问题时显得很困难,甚至无能为力.因此,越来越多的研究人员将思路转变到群智能算法中,从自然界中生物的群体行为得到启发,提出将新型智能算法(如遗传算法、细菌算法,狼群算法和粒子群算法等[1-2])应用在函数优化中,并得到了一定效果.上述算法在解决函数优化问题时表现出强大的能力和优势,但仍有不足,因此,人们仍在继续探索研究新的启发式智能优化算法或混合算法等.
粒子群算法被广泛应用的原因是相较于其他群智能算法,粒子群算法具有结构简单,参数易调整,优化结果明显等优点.当然,粒子群搜索算法也存在一些不足,如PSO算法易进入早熟和局部最优等[3].然而由于PSO算法在很多领域内总体上都表现出了强大能力,其理论和应用方面受到国内外许多学者的重视和进一步研究.文献[4]采用新的粒子编码方式与位置更新方式,提高了标准粒子群算法的收敛速度;文献[5]更改了传统惯性权重,依据粒子本身的进化经验,实现自适应调整,提高了算法的多样性和算法的寻优能力;文献[6]有效改变了粒子数目和算法中的速度位移方程,使得改进算法的收敛速度和收敛精度都得到了明显改善和提高.随着多种群智能算法的不断发展,由两种或多种算法的相结合达到相互取长补短的混合算法得到广泛应用.文献[7]将量子行为思想引入到PSO系统中,通过改变粒子更新方式,改进了PSO算法.改进PSO算法虽能在一定程度上改善标准粒子群算法的不足,但效果仍不理想,为了能够进一步提高PSO算法的收敛精度,本文在对粒子群算法和模拟退火算法进行了进一步研究后,提出了基于模拟退火的粒子群算法,该算法具有较强的全局搜索能力,在接受新解时既可以接受好解又可以接受差解.将本文算法应用到标准粒子群算法中,可以保证种群的多样性,有利于跳出局部最优解,提高算法的收敛速度和寻优精度,并避免“早熟”现象的发生.
1 基本粒子群算法
粒子群(PSO)算法是应用较广的一种算法,最早是在1995年由Kennedy和Eberhart提出来的,该算法是一种对自然界鸟群、鱼群等在群体生活中的捕食与移动过程的一种近似模拟[2].粒子群算法通过不断迭代来搜寻目标函数的最优值,初始化一组随机解,而每个粒子都可看成是问题的潜在解.鸟群能否成功捕获到食物不仅与过去积累的经验和认知有关,同时还和群体中的其它个体之间存在联系[8].在粒子群算法中粒子在解空间追随最优粒子进行搜索,在搜索过程中速度和位置信息是在不断调整改变的,其主要依据是粒子过去积累的经验和群体中的其它个体信息等.在PSO算法初始化过程中随机产生粒子群的种群,其中每个粒子都是目标函数的解,为了寻找函数的最优解,每个粒子会根据个体历史最优位置和种群的最优位置来多次调整自身的速度和位置更新策略,并经多次迭代寻优最终找到问题的最优解.
在PSO算法中,每个粒子都可以看作多维搜索空间中优化问题的解.假设在一个D维搜索空间中某群体中共有n个粒子,第i个粒子在D维搜索空间中的位置向量Xi=(xi1,xi2,…,xiD),每个粒子的位置代表一个潜在解,代入目标函数就可以计算其适应度值.第i个粒子的速度向量为Vi=(vi1,vi2,…,viD),利用目标函数求解其适应度值,确定个体最优位置向量Pi=(pi1,pi2,…,piD)与当前情况下群体所经历的历史最优位置向量Pg=(pg1,pg2,…,pgD).粒子群算法对粒子操作时涉及的更新公式[9]为
vij(t+1)=ωvij(t)+c1r1(pij(t)-xij(t))+
c2r2(pgj(t)-xij(t))
(1)
xij(t+1)=xij(t)+vij(t+1)
(2)
式中:c1和c2为加速常数,分别调节粒子向自身最优位置与向全局最优位置飞行的步长,通常c1+c2≤4;r1和r2为两个相互独立的随机函数;ω为惯性常数,可以平衡全局与局部搜索能力;xij(t)为第i个粒子在t时刻的第j维位置分量;vij(t)为第i个粒子在t时刻的第j维速度分量;pij(t)为第i个粒子的第j维分量更新前的历史最优位置;pgj(t)为t时刻种群所经历的最优位置.
式(1)由三项组成:第一项为粒子的当前速度,即现在状态部分;第二项为粒子从自身出发的自我认知部分;第三项为粒子在整个群体中与其它粒子间进行协调的社会部分.通过公式(1)、(2)不断更新,粒子不断向全局最优解靠拢,寻找搜索空间中的最佳值.基本粒子群算法需要用户确定的参数并不多,而且操作简单,故使用比较方便.但是它的缺点是易陷入局部极值点,搜索精度不高,因此,人们提出了许多改进算法,从而在一定程度上改进了基本粒子群算法的性能[10].
2 模拟退火算法
模拟退火(SA)算法不仅是一种统计优化方法,还是一种全局优化算法.该算法从物理退火原理得到启发,最早由Metropolis提出.当固体物质不断升温时,随着温度的增加,物质内部的粒子变得活跃起来并处于不稳定状态;与之相反,当温度不断降低时,物质内部粒子的活跃度又在不断下降,从不稳定状态变成稳定状态.依照固体物质退火过程和组合优化问题的共性特点,将模拟退火算法应用于各种组合优化问题中.
SA算法在对目标问题进行迭代优化寻找最优解时,首先需要确定一个初始温度,并在问题解空间上生成一个初始状态作为初始解,然后对当前初始状态进行干扰,模拟固体内部粒子在一定温度下的状态转移过程.之后评估由干扰得出的新解,将新解和当前解进行比较并根据Metropolis准则进行替换.SA算法以概率1来接受最优解,以某种概率来接受较差解.正因为具有这种能力,所以该算法不易陷入局部最优陷阱,从而可以跳出局部最优解.Metropolis准则定义了物体在某一温度T下从状态i转移到状态j的内能概率,其表达式为
(3)
式中:E(i)和E(j)分别为固体在状态i和j下的内能;ΔE为内能增量;K为波尔兹曼常数.
由式(3)可知,当E(j)
3 模拟退火粒子群算法
粒子群算法在函数优化过程中主要依赖粒子之间的信息不断更新粒子的位置和速度,使其不断向最优解方向靠拢.PSO算法存在易早熟,易陷入局部最优,后期收敛速度较慢,搜索精度较差等缺点.模拟退火算法具有很强的全局搜索能力,存在接受较差解的可能,在运算时遇到较差解能够以一定的概率接受,从而可以跳出局部最优解陷阱,收敛于全局最优解区域,拥有较高的搜索精度.但在算法运算时,因其需要非常高的退火温度,故收敛速度十分缓慢.
PSO算法和SA算法各具优缺点,结合SA算法中的Metropolis准则并与PSO算法相互融合形成一种模拟退火粒子群混合优化(SAPSO)算法.该混合算法以基本粒子群算法运算流程作为主体流程,把模拟退火机制引入其中并实现取长补短,明显克服PSO算法早熟收敛的弊端,改善SA算法收敛速度慢的缺点,从而提升了算法的整体性能.模拟退火粒子群算法流程如图1所示.
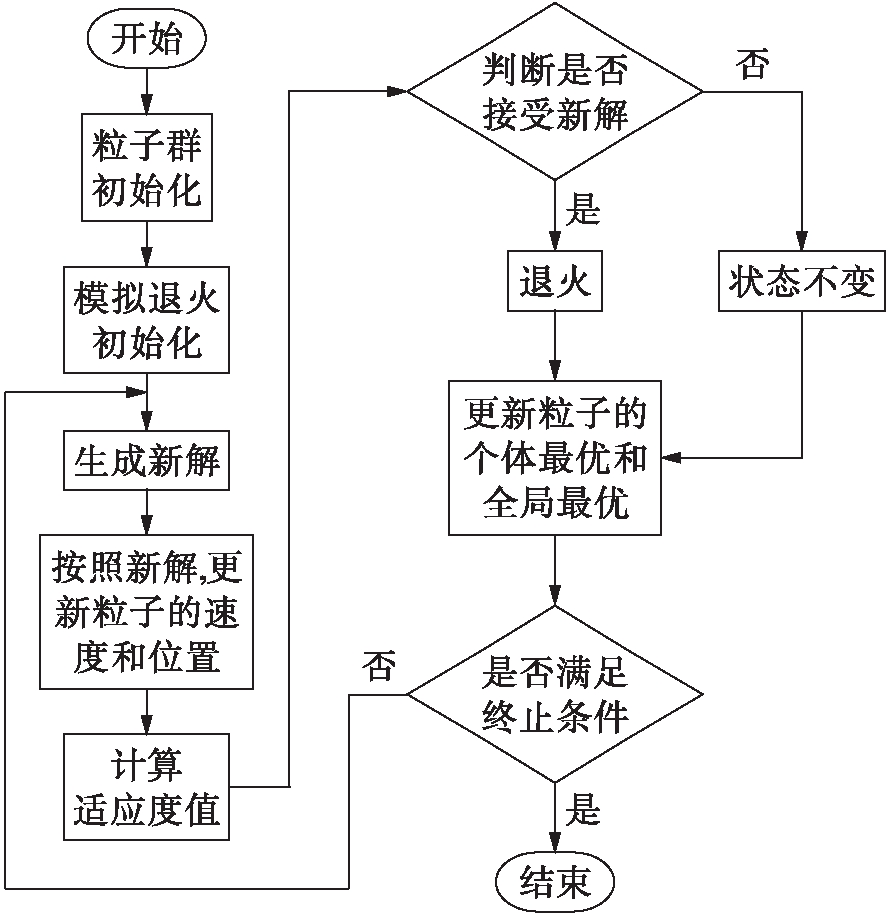
图1 模拟退火粒子群算法流程
Fig.1 Flow chart of SAPSO algorithm
利用模拟退火粒子群算法进行函数优化时的具体步骤为:
1)对粒子群里的相关参数进行初始化,如种群、迭代次数、粒子维度、粒子速度和位置等,并计算初始粒子群的适应度及相关参数.
2)模拟退火初始化过程,设置初始温度,生成初始解S,求出评价函数C(S),并令C(S)为全局最优解.
3)生成新解S′.
4)按照式(1)、(2)更新粒子的速度和位置,并计算适应度值.
5)求得C(S′)=min{f(xi)},ΔC=C(S′)-C(S),其中,f(xi)为最小适应度值.若ΔC<0或exp(-ΔC/T)>rand(0,1),C(S)=C(S′),S=S′,并接受由S′所更新的速度和位置;否则将拒绝S′的值,采用当前时刻值来更新速度和位置,并计算适应度值.
6)根据适应度值来更新全局最优解和局部最优解.
7)判断是否满足结束条件,若满足,输出最优值;若不满足,转到步骤3).
4 仿真实验
4.1 测试函数
为了检验SAPSO混合算法的优化效果,选取了PSO和GA算法进行对比实验,并引入5个非线性函数进行测试.5个测试函数分别为Sphere、Rosenbrock、Ackley、Griewank和Rastrigrin函数.除了Rosenbrock函数在全局最优解[1,1,…,1]处具有极小值外,其余测试函数均在全局最优解[0,0,…,0]处具有极小值,且极小值均为0,函数最优值也均为0.测试函数具体表达式如表1所示.
表1 测试函数
Tab.1 Test functions

函数表达式定义域Spheref1(x)=∑ni=1x2i[-100,100]Rosenbrockf2(x)=∑n-1i=1(100(xi+1-x2i)2+(xi-1)2)[-10,10]Ackleyf3(x)=-20exp(-0.21n∑ni=1x2i)-exp(1n∑ni=1cos(2πxi))+20+e[-5,5]Griewankf4(x)=∑ni=1x2i/4000-∏ni=1cos(xi/i)+1[-10,10]Rastrigrinf5(x)=∑ni=1(x2i-100cos(2πxi)+10)[-10,10]
4.2 结果与分析
利用SAPSO、PSO和GA算法对上述5个测试函数进行数值模拟来验证本文算法可行性.主要参数设置为:种群规模40;最大迭代次数1 000;函数维度30.PSO算法中惯性权重初始最大值为0.9,惯性权重初始最小值为0.4;c1=1.49,c2=1.49.退火算法中K=0.7,初始温度为10 000 ℃;遗传算法中交叉概率为0.7,变异概率为0.3.
为了验证模拟退火粒子群混合算法的优越性和可行性,通过对表1中的5个非线性测试函数进行对比分析,得出Sphere、Griewank、Rosenbrock、Ackley和Rastrigrin函数的优化曲线,结果如图2~6所示.
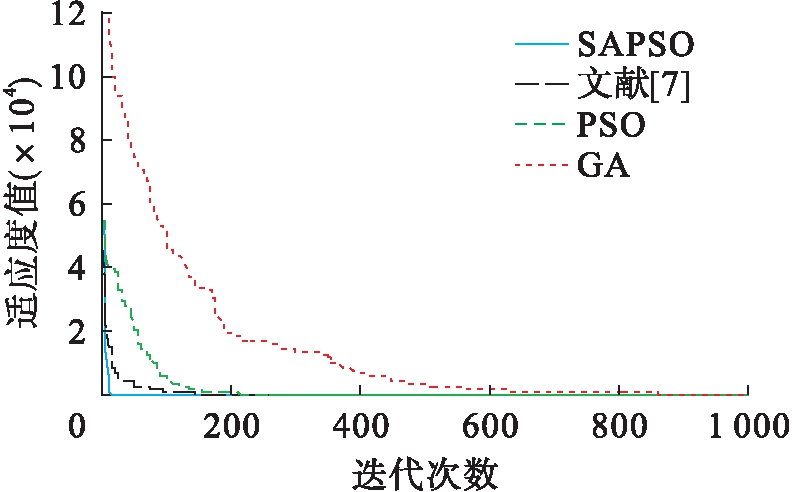
图2 Sphere函数优化曲线
Fig.2 Optimization curves of Sphere function
由图2~6可见,与粒子群算法和遗传算法相比,基于模拟退火的粒子群混合算法在高维函数优化中具有明显优势,混合算法易跳出局部最优解,避免“早熟”现象且具有收敛速度快等优点,克服了传统PSO算法和GA算法中出现的不足和缺点.
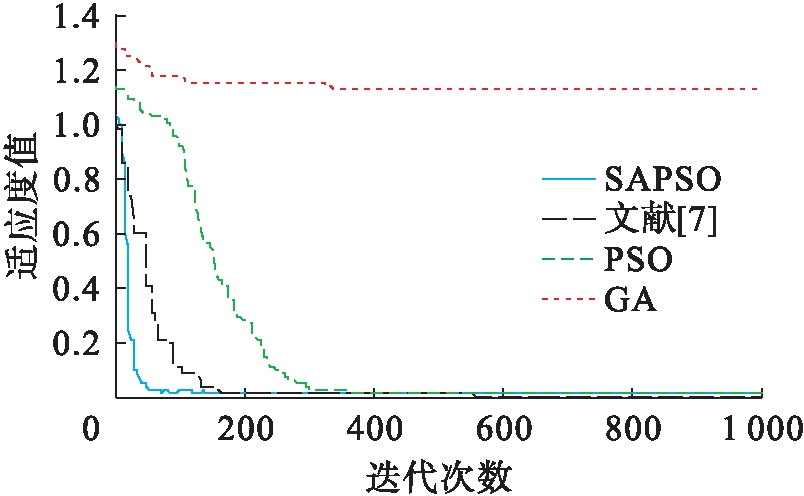
图3 Griewank函数优化曲线
Fig.3 Optimization curves of Griewank function
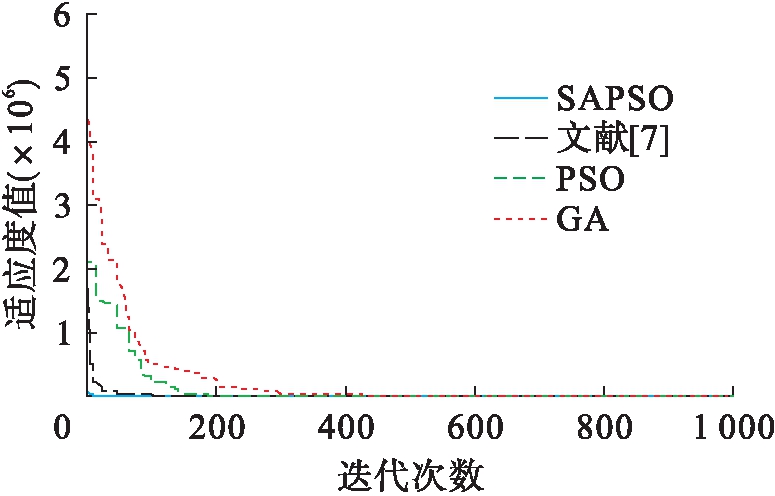
图4 Rosenbrock函数优化曲线
Fig.4 Optimization curves of Rosenbrock function
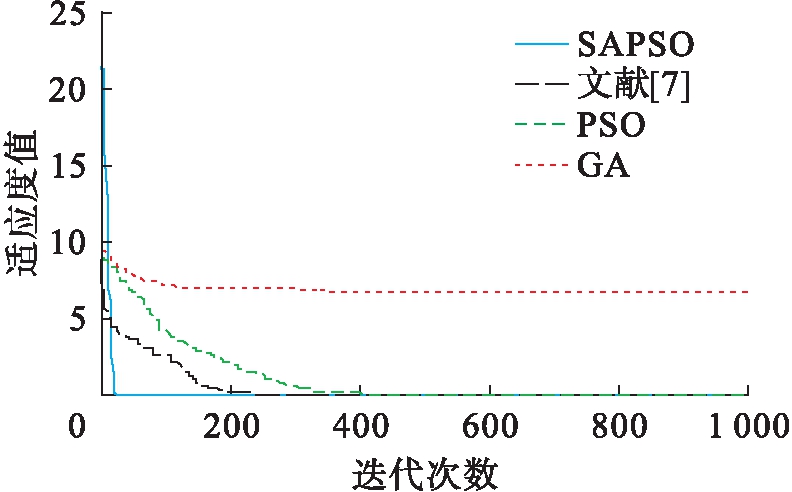
图5 Ackley函数优化曲线
Fig.5 Optimization curves of Ackley function
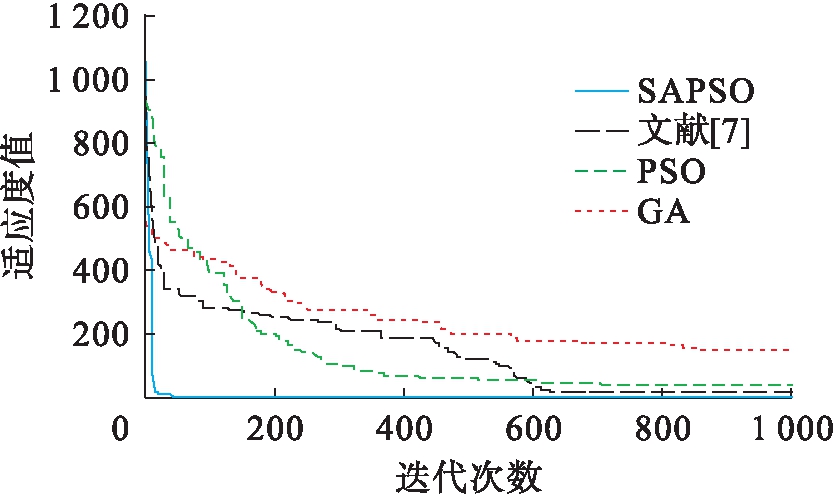
图6 Rastrigrin函数优化曲线
Fig.6 Optimization curves of Rastrigrin function
5 结 论
针对传统PSO算法易出现局部最优等缺点,在标准粒子群算法的基础上引进模拟退火算法思想,提出了模拟退火粒子群混合算法.该混合算法利用模拟退火算法的概率突变能力,不仅能接受最优解,还能以某种概率来接受较差解.因此,混合算法不易陷入局部最优的陷阱,从而具有跳出局部最优解的能力.该混合算法不仅基本保持了粒子群优化算法简单易实现的特点,而且能够增强粒子群算法的全局寻优能力,加快了算法的进化速度,提高了算法的收敛精度.利用5个测试函数对模拟退火粒子群混合算法进行测试后发现,与PSO和GA算法相比,本文算法具有较快的收敛性和较好的稳定性,从而验证了本文算法的有效性.
[1] 高鹰,谢胜利.基于模拟退火的粒子群优化算法 [J].计算机工程与应用,2004(1):47-50.
(GAO Ying,XIE Sheng-li.Particle swarm optimization algorithm based on simulated annealing [J].Computer Engineering and Application,2004(1):47-50.)
[2] 马松涛.复杂优化问题中小生境粒子群优化算法的改进及研究 [D].郑州:郑州大学,2013.
(MA Song-tao.Improvement and research of niche particle swarm optimization algorithm for complex optimization problems [D].Zhengzhou:Zhengzhou University,2013.)
[3] 池元成,方杰,魏鑫,等.基于小生境和交叉选择算子的改进粒子群优化算法 [J].系统仿真学报,2010,22(1):111-114.
(CHI Yuan-cheng,FANG Jie,WEI Xin,et al.Improved particle swarm optimization algorithm system simulation based on niche and cross selection [J].Journal of System Simulation,2010,22(1):111-114.)
[4] 于琳,孙莹,徐然,等.改进粒子群优化算法及其在电网无功分区中的应用 [J].电力系统自动化,2017,41(3):89-95.
(YU Lin,SUN Ying,XU Ran,et al.Improved particle swarm optimization algorithm and its application in power grid reactive power division [J].Automation of Electric Power Systems,2017,41(3):89-95.)
[5] 杨智,陈颖.改进粒子群算法及其在PID整定中的应用 [J].控制工程,2016,23(2):161-166.
(YANG Zhi,CHEN Ying.Improved particle swarm optimization algorithm and its application in PID tuning [J].Control Engineering,2016,23(2):161-166.)
[6] 吴辰斌,李海明,刘栋,等.一种改进型粒子群优化算法在电力系统经济负荷分配中的应用 [J].电力系统保护与控制,2016,44(10):44-48.
(WU Chen-bin,LI Hai-ming,LIU Dong,et al.An im-proved particle swarm optimization algorithm for power system economic load allocation [J].Power System Protection and Control,2016,44(10):44-48.)
[7] 王锦坤,邱碧丹.基于量子粒子群算法的主动配电网优化调度研究 [J].机电信息,2016,38(24):142-143.
(WANG Jin-kun,QIU Bi-dan.Research on optimal dispatching of active distribution network based on quantum particle swarm optimization algorithm [J].Electromechanical Information,2016,38(24):142-143.)
[8] 郑申海,胡小兵,郑满满,等.改进粒子群和模拟退火混合算法及其应用 [J].计算机技术与发展,2013,23(7):26-30.
(ZHENG Shen-hai,HU Xiao-bing,ZHENG Man-man,et al.Improved particle swarm optimization and simulated annealing hybrid algorithm and its application [J].Computer Technology and Development,2013,23(7):26-30.)
[9] 王杰,李慧慧,彭金柱.一种拟随机初始化模拟退火粒子群算法 [J].郑州大学学报(理学版),2016,48(3):75-81.
(WANG Jie,LI Hui-hui,PENG Jin-zhu.Quasi random initialization simulated annealing particle swarm optimization [J].Journal of Zhengzhou University (Science Edition),2016,48(3):75-81.)
[10] 周利军,彭卫,邹芳,等.自适应变异粒子群算法 [J].计算机工程与应用,2016,52(7):50-55.
(ZHOU Li-jun,PENG Wei,ZOU Fang,et al.Adaptive mutation particle swarm optimization algorithm [J].Computer Engineering and Application,2016,52(7):50-55.)