自由场地的动力响应计算问题一直是岩土地震工程中具有理论和实际意义的研究课题[1-2].通过自由场地的震动响应分析研究可以指导地下结构和临近建筑物地基等抗震设防措施,为安全抗震技术提供可靠数据[3].其中,1995年日本阪神地震中,大开车站由于场地液化发生严重破坏,车站中柱发生垮塌,地表沉陷2.5 m以上,并存在大量积水.由于可液化场地动力特性的复杂性,目前针对可液化地基场地震害破坏机理研究还不是很成熟,因此,开展可液化自由场地震动研究是有必要的.
在可液化自由场地动力特性研究方面,凌贤长和苏栋等[4-5]开展了自由场地振动台试验对场地震动特性的研究;高孟潭和杨繁等[6-7]基于等效线性化方法对自由场地震动特性进行了研究.由于地震动力特性研究的复杂性,采用简化方法进行评估不能真实反映土体非线性对地震反应的实际影响,而普通(离心机)振动台试验具备重力失真(科里奥利现象)等不足,因此,数值分析方法是重要关键的研究手段.其中,董云[8]、邹炎[9]、刘涛[10]、崔春义[11]等基于动力非线性有限元数值方法对自由场地震动特性进行了研究.
由于问题自身的复杂性及计算理论、硬件限制,在自由场地地震动力特性研究中,关于综合考虑饱和土多孔介质性和土动力本构非线性的研究较少.因此,本文将结合开源有限元程序OpenSEES计算平台,基于Biot动力固结方程,采用固液两相介质有效应力完全耦合的数值计算方法,建立饱和可液化自由场地数值计算模型,进行饱和可液化自由场地地震动作用下动力响应特性分析.
1 有限元模型
1.1 砂土本构模型
参考由Yang等[12]修正的多屈服面塑性本构模型,其屈服面方程为
M2(p′+p′0)2
(1)
式中:s为偏应力张量,s=σ′-p′δ,σ′为有效应力张量,δ为克朗内克符号;α为偏应力空间中屈服面在π偏应力平面上的中心点坐标;M为屈服面大小,M=6sin φ/(3-sin φ),φ为摩擦角;p′为有效应力;p′0=-c/tan φ,c为粘聚力;“∶”为张量双点积运算.主应力空间和偏平面上的屈服面[12]如图1所示.
1.2 黏土本构模型
本文中黏土本构采用OpenSEES中的Pressure Independ Multi Yield,简称PIMY本构模型.该本构模型可模拟土体的弹塑性性质,塑性性质体现在偏应力-应变关系上,体积应力-应变关系为线弹性且与偏分量不相关[12].PIMY模型屈服面方程为
(2)
黏土多屈服面塑性本构强化法则采用偏量随动强化法则,屈服面位置可以在偏应力空间平移而大小不改变,对于屈服面运动规则,规定任意两个屈服面fm+1和fm只能相交于一点,且在该点具有相同的外法线,在此假设条件下,屈服面运动张量定义为
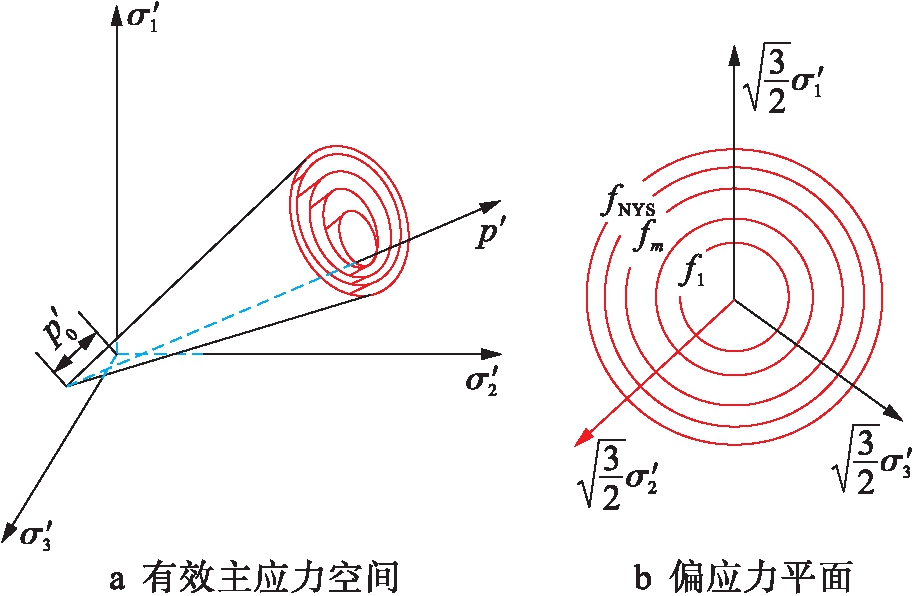
图1 主应力空间和偏平面上的屈服面
Fig.1 Principal stress space and yield plane on deviatoric plane
(3)
式中:sT为二阶偏应力张量,表示屈服面fm+1和fm交点T的偏应力张量;αm和αm+1分别为屈服面fm和fm+1中心点坐标;Mm和Mm+1为屈服面大小.
1.3 数值模型
在OpenSEES中建立70 m×20 m平面应变模型,网格尺寸1 m×1 m.土体采用土水完全耦合的quadUP单元,模型两侧边界采用捆绑边界,约束底部边界,地面为自由边界条件.土体采用5%的瑞利阻尼[13].自由场地土体网格数值模型如图2所示.土层基本物理力学参数如表1所示.

图2 数值模型
Fig.2 Numerical modelling
本文地震波选用El-Centro波,地震动时程曲线与傅氏谱曲线如图3所示,峰值强度为0.2g,地震波持续时间为30 s,计算过程分两步进行:先施加重力步进行静力计算,用来模拟初始地应力平衡;基岩输入水平地震动进行动力计算.
2 结果分析与讨论
2.1 可液化自由场地加速度及其频谱响应
选取场地中轴线为典型特征垂线,并取特征垂线上各土层分界点为特征点,其中特征点A、B、C、D处分别在特征垂线上土层20、13、6、2 m深度处.图4为特征垂线上加速度放大系数变化曲线.可以看出,靠近基岩处的硬质黏土层地震动加速度放大系数小于1.而在砂土层深度区域,加速度放大系数呈现出随深度减小而逐渐增大的变化规律.在土层深度约4 m深度范围内,由于该区域砂土层发生液化,而液化土体对剪切波传播作用极弱,因而此深度范围加速度放大系数发生突变.
表1 土层物理力学参数
Tab.1 Physical and mechanical parameters for soil
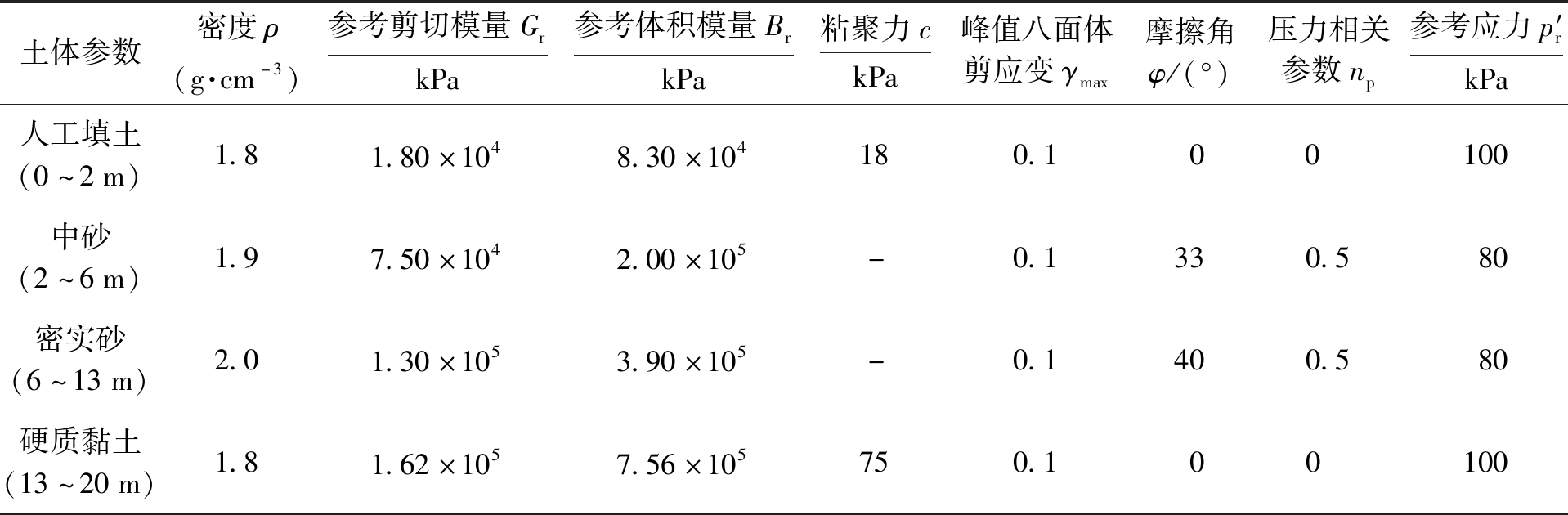
土体参数密度ρ(g·cm-3)参考剪切模量GrkPa参考体积模量BrkPa粘聚力ckPa峰值八面体剪应变γmax摩擦角φ/(°)压力相关参数np参考应力p′rkPa人工填土(0~2m)1.81.80×1048.30×104180.100 100中砂(2~6m)1.97.50×1042.00×105-0.1330.580密实砂(6~13m)2.01.30×1053.90×105-0.1400.580硬质黏土(13~20m)1.81.62×1057.56×105750.100100
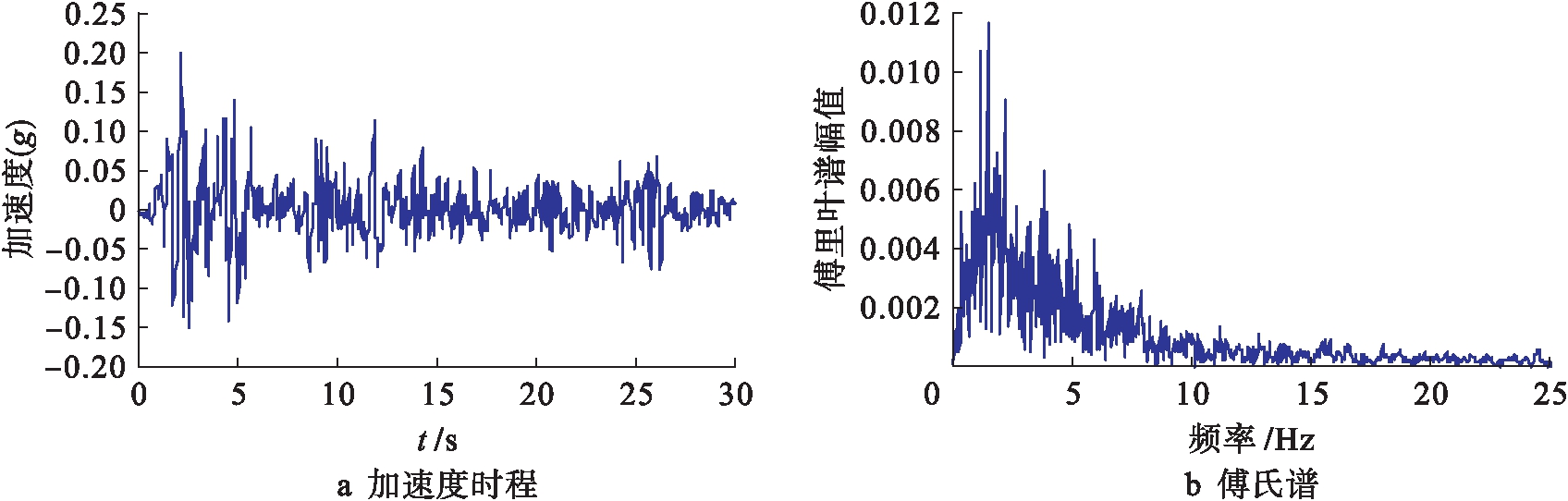
图3 El-Centro波时程曲线与傅氏谱
Fig.3 Time-history curve of El-Centro wave and Fourier spectrum
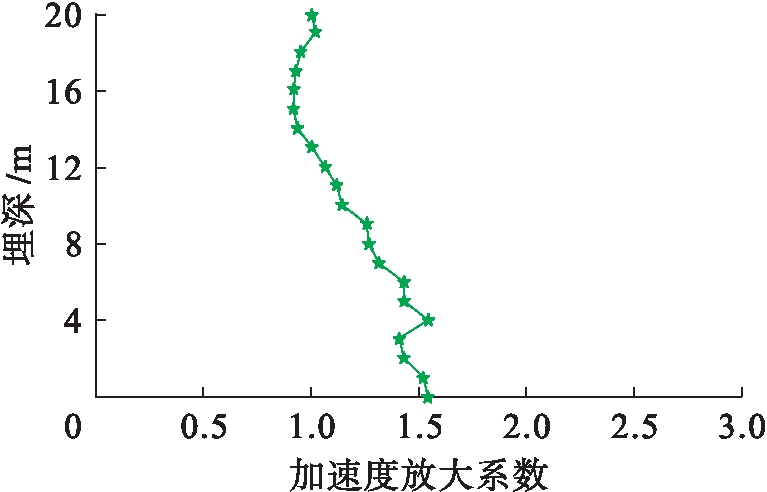
图4 特征线上加速度放大系数
Fig.4 Acceleration magnification coefficient on characteristic line
图5、6分别为特征垂线上各深度处傅里叶谱和功率谱变化曲线.由图5、6可知,由于可液化场地高频滤波作用,地震波由基岩沿特征线向上传播过程中,高频成分幅值逐渐减弱而低频成分幅值逐渐呈现增大趋势,且频带主要集中于0~5 Hz范围内.
图7为特征垂线上不同土层深度特征点处β谱曲线对比.由图7可知,土层沿深度变化情况对地震动β谱曲线具有显著影响.在埋深13~20 m(特征点A~B)的硬质黏土范围内,β谱极值由基岩部分的5.1增加到6.9,卓越周期平台双峰现象显著,主要集中在0.3~0.8 s周期范围内.
在埋深6~13 m(特征点B~C)范围内的密实砂土层内,卓越周期平台变窄,β谱双峰现象减弱,谱极值集中在0.5 s附近,相较于硬质黏土层,其更容易对低周期地震波产生放大效应.在埋深2~6 m(特征点C~D)范围内的砂土层,峰值平台主要集中于0.2~0.4 s周期范围内,且对低周期成分更为敏感.在埋深0~2 m(特征点D至地表)范围的人工填土层,土体对低周期成分反应更为明显,且相同周期对应的峰值水平,在地表处要大于埋深2 m(特征点D)处峰值.不难看出,该场地中土层分布情况呈现出典型的高频滤波、低频放大现象.即地震波由基岩沿特征线向上传播过程中,对应β谱曲线卓越平台呈现逐渐变窄的变化趋势.
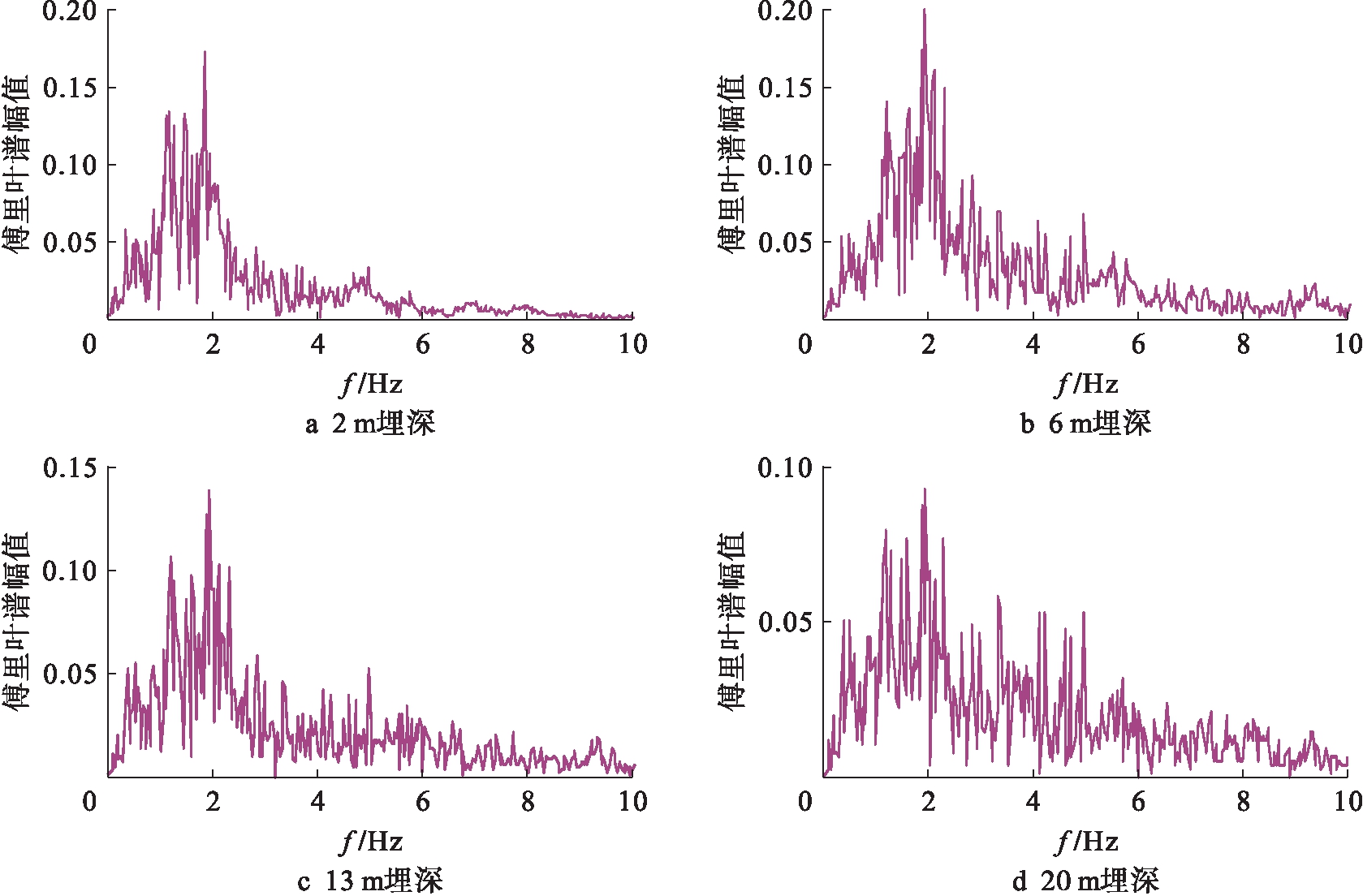
图5 特征线上各深度处傅里叶谱
Fig.5 Fourier spectrum on characteristic line at various depths
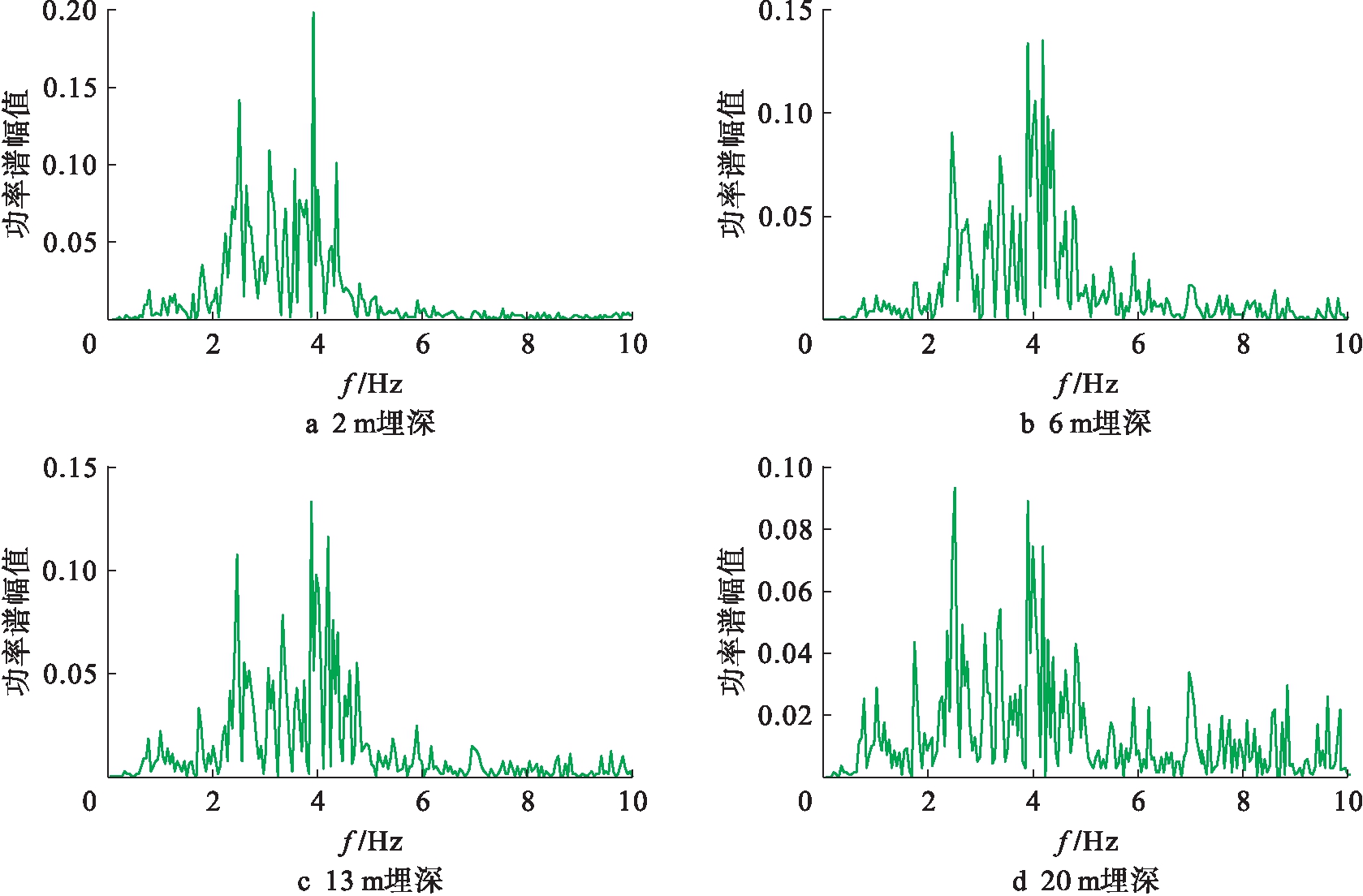
图6 特征线上各深度处功率谱
Fig.6 Power spectrum on characteristic line at various depths
2.2 可液化自由场地孔压动力响应分析
图8为特征点处动孔压比时程变化曲线.由图8可知,震动初期孔隙水压力快速增长,短时间内达到峰值水平后,动孔压幅值水平发生小幅震荡并趋于稳定.随着土层埋深和土层密实度增加,砂土层内的液化趋势明显减弱.其中,13 m深度处特征点动孔压比峰值水平仅约为0.35.
2.3 可液化自由场地地震位移响应分析
图9为特征垂线上不同土层深度特征点体应变时程曲线.由图9可知,埋深4~6 m的砂土层发生显著的负体应变,主要是由于地震荷载使饱和砂土发生剪缩,而黏土层的变化相对较小.
图10为特征垂线上各深度处竖向位移时程曲线对比.由于饱和砂土和黏土层在地震作用下会分别发生剪缩效应和循环软化效应,进而使得土体产生不可恢复的残余变形.由图10可知,场地各深度处均发生了一定程度的竖向变形.其中,地表在震后沉降约为13 mm.
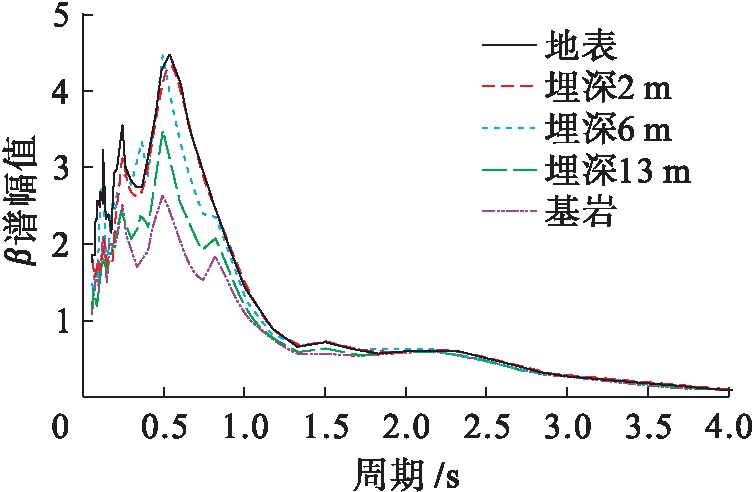
图7 特征线各深度处β谱
Fig.7 β-spectrum on characteristic line at various depths
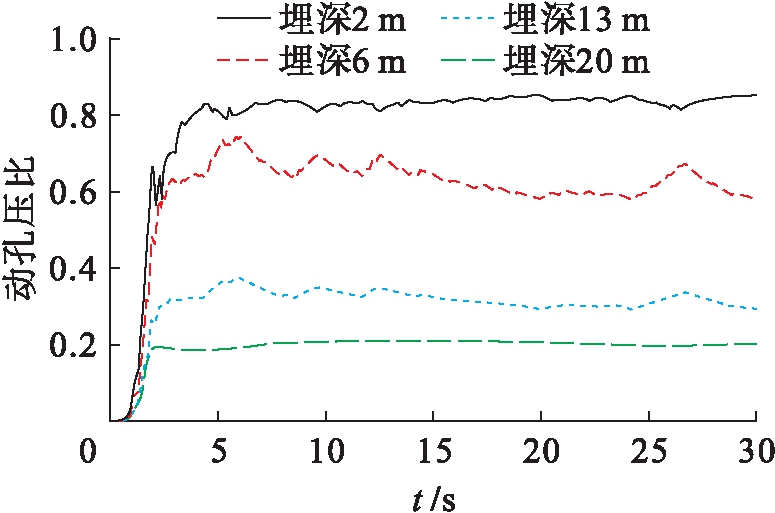
图8 特征线各深度处动孔压比时程曲线
Fig.8 Time-history curves of dynamic pore pressure ratio on characteristic line at various depths
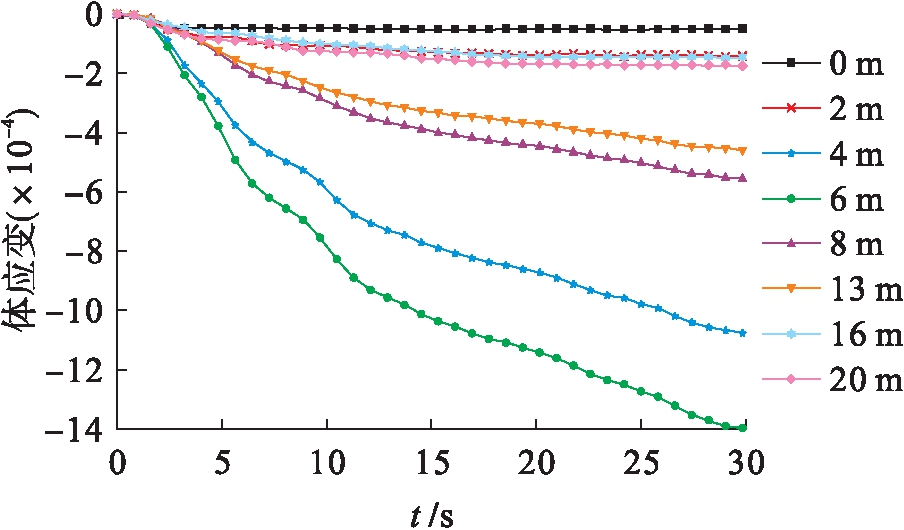
图9 特征线上体应变时程曲线
Fig.9 Time-history curves of body strain on characteristic line
3 结 论
本文基于饱和两相多孔介质耦合理论建立了饱和自由可液化场地动力分析有限元模型,研究了自由场不同土层特征点处地震加速度及其频谱、动孔压比、竖向位移等动力响应变化规律,研究结果表明:
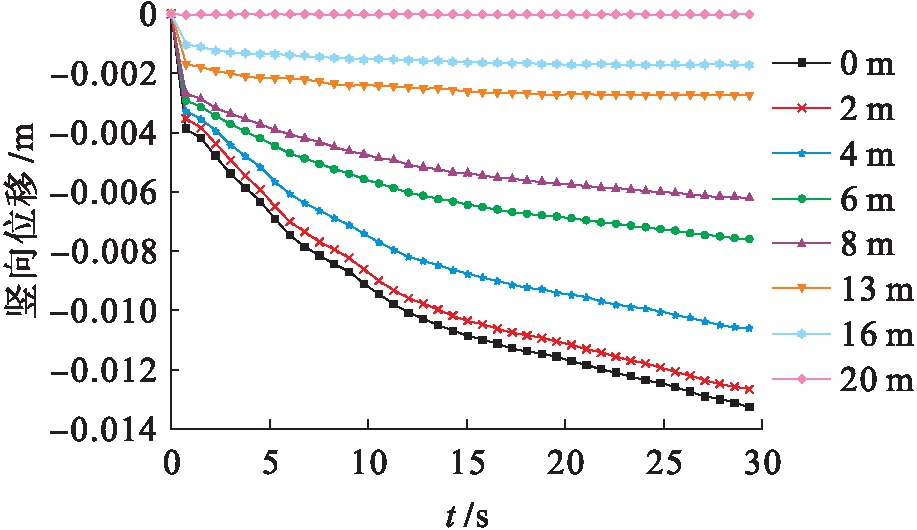
图10 特征垂线上竖向位移时程曲线
Fig.10 Time-history curves of vertical displacement on characteristic line
1)加速度放大系数随砂土层深度减小而增大,液化土体对剪切波传播作用较弱使得加速度放大系数在砂土层液化区深度处发生突变;
2)饱和可液化砂土场地β谱曲线卓越平台宽度随液化层深度的增加而逐渐变窄,土层存在典型的高频过滤、低频放大效应;
3)震动初期孔隙水来不及排出,动孔压短时间内迅速增大并达到峰值,且随着土层深度和密实度增加,其液化趋势明显减弱.
[1] 徐源,丛龙.考虑土-结构相互作用的框架结构地震时程分析 [J].沈阳工业大学学报,2014,36(5):596-600.
(XU Yuan,CONG Long.Seismic time history analysis for frame structure with considering soil-structure interaction [J].Journal of Shenyang University of Technology,2014,36(5):596-600.)
[2] Vessia G,Venisti N.Liquefaction damage potential for seismic hazard evaluation in urbanized areas [J].Soil Dynamic and Earthquake Engineering,2013,31(8):1094-1105.
[3] Sarah D,Soebowo E.Liquefaction due to the 2006 Yogyakarta Earthquake:field occurrence and geotechnical analysis [J].Procedia Earth and Planetary Science,2013,6:383-399.
[4] 凌贤长,王臣,王志强,等.自由场地基液化大型振动台模型试验研究 [J].地震工程与工程振动,2003,23(6):138-143.
(LING Xian-zhang,WANG Chen,WANG Zhi-qiang,et al.Study on large-scale shaking table proportional model test for free-ground liquefaction arisen from earthquake [J].Earthquake Engineering and Engineering Vibration,2003,23(6):138-143.)
[5] 苏栋,李相崧.地震作用下自由场中饱和砂土的应力-应变推导 [J].岩土力学,2010,31(1):277-281.
(SU Dong,LI Xiang-song.Derivation of stress and strain of saturated sand in free ground under seismic loading [J].Rock and Soil Mechanics,2010,31(1):277-281.)
[6] 高孟潭,陈学良,肖和平,等.湖南中强地震活动地区Ⅱ类场地放大效应研究 [J].中国地震,2009,25(2):140-150.
(GAO Meng-tan,CHEN Xue-liang,XIAO He-ping,et al.Study on amplification effect of type Ⅱ sites in moderate earthquake area of Hunan [J].Earthquake Research in China,2009,25(2):140-150.)
[7] 杨繁,王敏,王国波,等.自由场地土体非线性地震响应研究 [J].中国安全科学学报,2014,24(7):117-122.
(YANG Fan,WANG Min,WANG Guo-bo,et al.Research on nonlinear seismic response of free-field soil [J].China Safety Science Journal,2014,24(7):117-122.)
[8] 董云,楼梦麟.基于饱和多孔介质的复杂自由场地震响应分析 [J].同济大学学报(自然科学版),2014,42(2):199-203.
(DONG Yun,LOU Meng-lin.Seismic response analysis of complicated soil site based on saturated porous media [J].Journal of Tongji University (Natural Science),2014,42(2):199-203.)
[9] 邹炎,景立平,崔杰,等.基于可液化场地地震反应数值模拟的影响因素分析 [J].防灾减灾工程学报,2015,35(2):242-248.
(ZOU Yan,JING Li-ping,CUI Jie,et al.Factor analysis based on numerical simulation of liquefiable site’s seismic responses [J].Journal of Disaster Prevention and Mitigation Engineering,2015,35(2):242-248.)
[10] 刘涛.北部湾吹沙填海土动力特性与场地动力响应特征研究 [D].南宁:广西大学,2016.
(LIU Tao.Research of dynamic response and dynamic characteristics of soil in field of blowing sand reclamation of beibu gulf area [D].Nanning:Guangxi University,2016.)
[11] 崔春义,孟坤,梁志孟,等.深圳老街地铁车站自由场地地震动力特性数值分析 [J].沈阳建筑大学学报(自然科学版),2016,32(6):1008-1016.
(CUI Chun-yi,MENG Kun,LIANG Zhi-meng,et al.Seismic numerical analyses of free field around Shenzhen Laojie subway station [J].Journal of Shenyang Jianzhu University (Natural Science),2016,32(6):1008-1016.)
[12] Yang Z H,Elgamal A,Parra E.Computational model for cyclic mobility and associated shear deformation [J].Journal of Geotechnical and Geoenvironmental Engineering,2003,129(12):1119-1127.
[13] 李培河,戚承志.成层地基中不同土层分布对地下结构的抗震影响 [J].解放军理工大学学报(自然科学版),2014,15(5):457-461.
(LI Pei-he,QI Cheng-zhi.Effect of different soil layer distribution on seismic response of underground structure in layered foundation [J].Journal of PLA University of Science and Technology(Natural Science Edition),2014,15(5):457-461.)