地震中城市桥梁的破坏一般为桥墩的破坏,抗震安全性评估很大程度上是对桥墩的抗震安全性进行评估.对现有桥墩进行抗震性能评估是为了能估算出在常遇地震作用下桥墩构件的损失,或罕遇地震作用下发生严重损坏或倒塌的风险程度[1-7].只有对此有了明确的认知才能对桥墩整体性能的完整性和安全度做出合理的评估,对于危险程度高的桥墩构件采取相应的加固或减震措施.近年来,国内外学者对钢筋混凝土Y型桥墩抗震性能未有明确的评估措施,Y型桥墩的受弯性能和延性能力的研究尚未清楚[8-11].如何确保Y型桥墩在地震作用下的安全性是一个亟待解决的问题,因此,钢筋混凝土Y型桥墩的科学性和实用性评估对我国桥梁基于性能的抗震设计有着重要意义和参考价值.
1 有限元模型建立
运用有限元软件ABAQUS对钢筋混凝土结构模型进行受力分析时,必须首先确定材料的本构关系,即钢筋和混凝土材料的应力应变关系.材料的应力应变关系模型有很多,根据材料特性及荷载加载机制不同有所差异,但基本形状相似.
1.1 本构选择
钢筋本构选取经典的三折线模型,此模型省去了钢筋的二次塑流段,本文模拟的钢筋模型即是采用三折线模型.上世纪90年代由Lee、Fenves和Lubliner所创立的混凝土塑性理论是目前有限元分析软件ABAQUS所采用的塑性损伤模型的基础,混凝土的塑性损伤模型除了用于多种加载场合,例如单向加载、循环加载以及动态加载等,还具有较好的收敛性.
1.2 模型建立
假定混凝土和钢筋之间是理想粘结,选用ABAQUS有限元软件对钢筋混凝土Y型桥墩进行弹塑性模型模拟,并采用ABAQUS/Standard隐式分析模块进行求解,混凝土构件取20节点六面体单元C3D20R,钢筋选用桁架单元T3D2,图1为所建立的有限元模型.
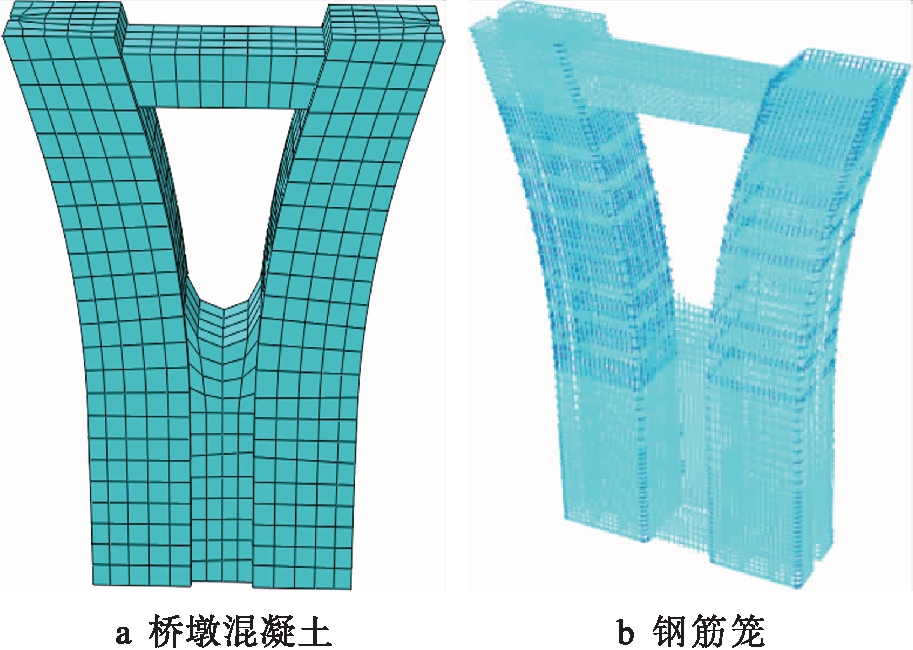
图1 Y型桥墩的有限元模拟模型
Fig.1 Finite element simulation model of Y-shaped pier
1.3 模型加载和边界条件
在ABAQUS软件中采用施加位移荷载方法分析非线性问题,此方法可以降低收敛的难度.具体的做法为:将位移荷载加载到参考点上,把参考点与桥墩的有效截面耦合.桥墩的墩底限制6个自由度,模拟整体现浇桥墩底部和承台之间采用刚接的连接形式,墩顶自由无约束,墩顶的截面处施加轴向压强.图2为模型的边界条件及加载示意图.
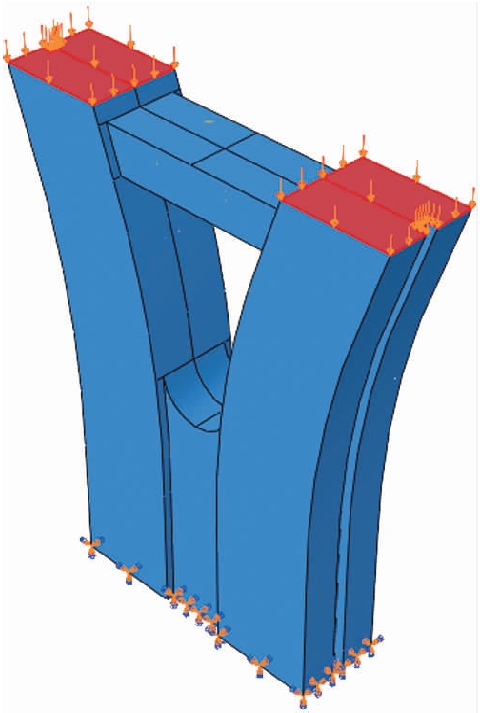
图2 模型的边界条件及加载示意图
Fig.2 Boundary condition and loading diagram of as-proposed model
2 桥墩截面抗震性能评估
2.1 桥墩截面弯矩-曲率分析
借助ABAQUS有限元分析软件对Y型桥墩模拟后,提取弯矩和曲率的关系曲线,如图3所示.对桥墩截面的弯矩-曲率曲线进行研究,进而从截面的层次对桥墩做一个初步简单的评估分析.假定两节点之间柱段内各截面的曲率线性变化如图3所示,可求得节点的曲率半径、转角和侧移,即可得到水平力、轴压力与节点曲率关系,考虑平截面假定及材料本构关系,可以确定出截面应变和应力分布.
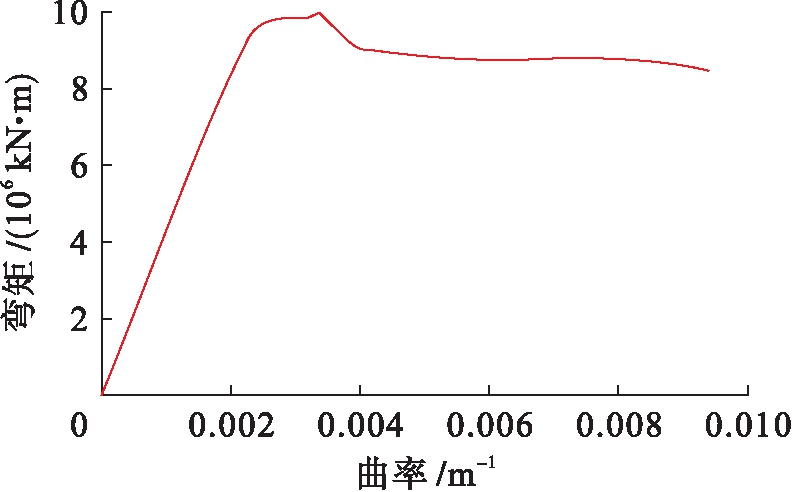
图3 杆件分段及曲率分布假定
Fig.3 Rod subsection and assumed curvature distribution
Y型桥墩两肢臂的截面分别为矩形截面,桥墩U形槽以下至墩底的截面是三个矩形截面,在顺桥向进行push-over推拉过程中,Y型桥墩截面相当于普通的矩形桥墩.令εy为纵筋的屈服曲率,对于常用的Ⅱ级钢筋,取εy=0.001 94,矩形截面的屈服曲率公式为
φyH=1.957εy
(1)
矩形截面的极限曲率公式为
(2)
式中:φy为截面屈服曲率;H为矩形截面计算方向的截面高度;φu为截面极限曲率;εs为钢筋极限拉应变,可取εs=0.09;P为截面所受到的轴力;f ′c为混凝土抗压强度标准值;Ag为混凝土截面面积.得到截面的屈服曲率和极限曲率之后,可以计算得到截面的曲率延性系数,即μφ=φu/φy.
2.2 轴压比对桥墩截面弯矩-曲率的影响
桥墩的抗震性能水平主要取决于桥墩截面的变形能力,本文对墩底矩形截面在不同轴力作用下的弯矩-曲率关系进行了分析,结果如图4所示.分析采用控制位移方法,在钢筋达到屈服强度时,截面也达到屈服曲率,所对应的弯矩即为屈服弯矩.
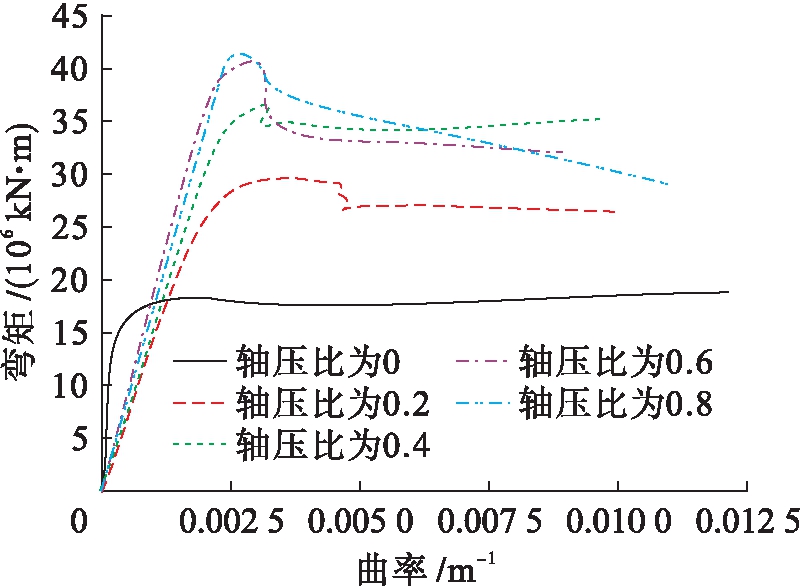
图4 Y型桥墩截面弯矩-曲率关系
Fig.4 Bending moment-curvature relationship for section of Y-shaped pier
由Y型桥墩截面弯矩-曲率关系曲线可知,墩底矩形截面的弯矩-曲率关系与轴压力的大小密切相关,轴压比为0时弯矩在很小的曲率变形下达到极限17×106 kN·m,表现出最陡峭的二折线属性,而后桥墩构件性能下降得很快直到破坏.轴压比为0.2时截面弯矩-曲率关系表征为三折线属性.曲率在0.004时弯矩有个骤降过程,这一过程桥墩的截面发生破坏,可能是因为受压区最大应变超过混凝土的极限压应变,或者拉压区钢筋破坏.轴压比为0.4时弯矩骤变,曲率相对轴压比为0.2时要小,前者的极限弯矩比后者大,此时轴压比对桥墩的变形产生了负面影响,但对桥墩的延性能力还未产生明显影响.轴压比大于0.6时,桥墩开始出现延性下降的情形.因此,轴压比在较小范围内时,轴压比的增大对桥墩的延性能力具有积极的影响,而超过一定值(约0.5)时,轴压比的增大开始产生负面的影响.
对曲线进行定量分析时不难看出,随着轴压比的增加,极限弯矩递增;极限弯矩在轴压比为0~0.4的过程中递增,在轴压比为0.4~0.8的过程中缓慢递减,其中0.4~0.6的极限弯矩很接近,轴压比约为0.5时可看作是极限弯矩的拐点;屈服弯矩和屈服曲率的变化趋势均递增.这表明随着轴压比的增大,其截面曲率延性系数在轴压比超过0.5之后随着轴向压力的增加会较慢递减,即轴压比约为0.5时,桥墩截面的延性能力最好.因此,桥墩上部合理的配重对提高桥墩的抗震性能意义重大.
2.3 桥墩截面抗震性能评估公式
1)强度提高系数.若考虑箍筋对受压构件截面核心区混凝土的约束作用,直接在模型中建立箍筋的方法显然是不经济的,可以通过混凝土的应力-应变全曲线方程来反应箍筋的作用,即采用约束混凝土本构模型,其中最常用的是Mander约束混凝土模型,其表达式为
(3)
(4)
式中:kc为混凝土强度提高系数;f ′l为有效约束应力;fco为混凝土单轴抗压强度;fcc为约束混凝土抗压强度.矩形截面x、y方向的约束混凝土有效约束应力为
f ′lx(y)=keρx(y)fyh
(5)
式中:fyh为横向钢筋屈服强度;ke为有效约束系数,对于矩形截面取ke=0.75~0.85;ρx(y)为x、y方向的配筋率,一般情况下,桥墩的力学配筋率在0.02~0.15之间.桥墩截面的抗弯性能和强度提高系数密切相关,对于约束混凝土的峰值应力受箍筋、拉筋、外包钢壁等约束性材料的影响较大,一般在计算中将强度提高系数取为1.1~1.3.Y形桥墩的矩形截面系数取值为1.13.
2)实际受压区高度系数.Y形桥墩是对称构件,其受压钢筋的面积必然等于受拉钢筋的面积.对于矩形截面,由混凝土规范可得
As fy-A′s fy-βξnfcbh0+p=0
(6)
式中:As为纵向受拉钢筋面积;A′s为纵向受压钢筋面积;fy为普通钢筋抗拉强度设计值;fc为混凝土抗压强度设计值;b为矩形截面宽度;h0为矩形截面有效高度;p为轴力;β为等效受压区高度系数;ξn为实际受压区高度系数,其表达式为
(7)
其中,ηk′为轴压比.
3)截面屈服曲率.由钢筋混凝土截面的几何关系和曲率相关公式可得
εcu=(c-d′)φu≈cφu=cμφφy=ξnh0μφφy
(8)
式中:c为极限拉应变;μφ为曲率延性系数;d′为受压端钢筋的保护层厚度.
另有国外学者Priestley等提出损伤控制极限状态下的混凝土极限压应变,其表达式为
(9)
式中:εsu为极限拉应变;ρs为约束钢筋的体积含筋率.
4)截面曲率延性系数.结合式(9),由矩形截面对应的截面参数,得到矩形截面钢筋混凝土桥墩的变形能力计算表达式为
(10)
由此可以看出,配筋率ωw一定时,只有受压区高度系数ξn与曲率延性系数μφ是不确定的.假设不考虑箍筋率参数的影响,即桥墩构件唯一时,式(10)可用于指导截面变形需求和截面几何尺寸.图5为μφ与ηk′的关系曲线,可知计算得到的曲线与有限元软件模拟出的曲率延性系数-轴压比曲线基本上是吻合的.
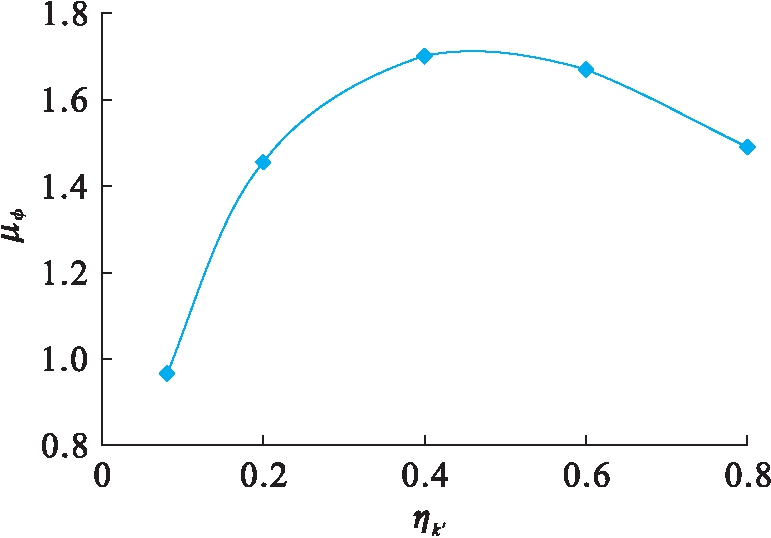
图5 轴压比与曲率延性系数关系曲线
Fig.5 Relationship curve for axial compression ratio and curvature ductility coefficient
3 桥墩构件抗震性能评估
3.1 桥墩位移延性能力
位移延性系数可以反映出结构或构件的变形能力.一般来说,延性系数越高的试件延性越好,位移延性系数越低的试件延性越差.为了了解桥墩模型的延性水平,采用位移延性系数表征试件的延性性能,并且定义位移延性系数为μ=Δu/Δy,其中,Δy为屈服位移,Δu为极限位移.由有限元模拟结果得到对比试验模型组的位移延性系数,如表1所示.
表1 轴压比和加载方向对位移延性系数的影响
Tab.1 Influence of axial compression ratio and loading direction on displacement ductility coefficient
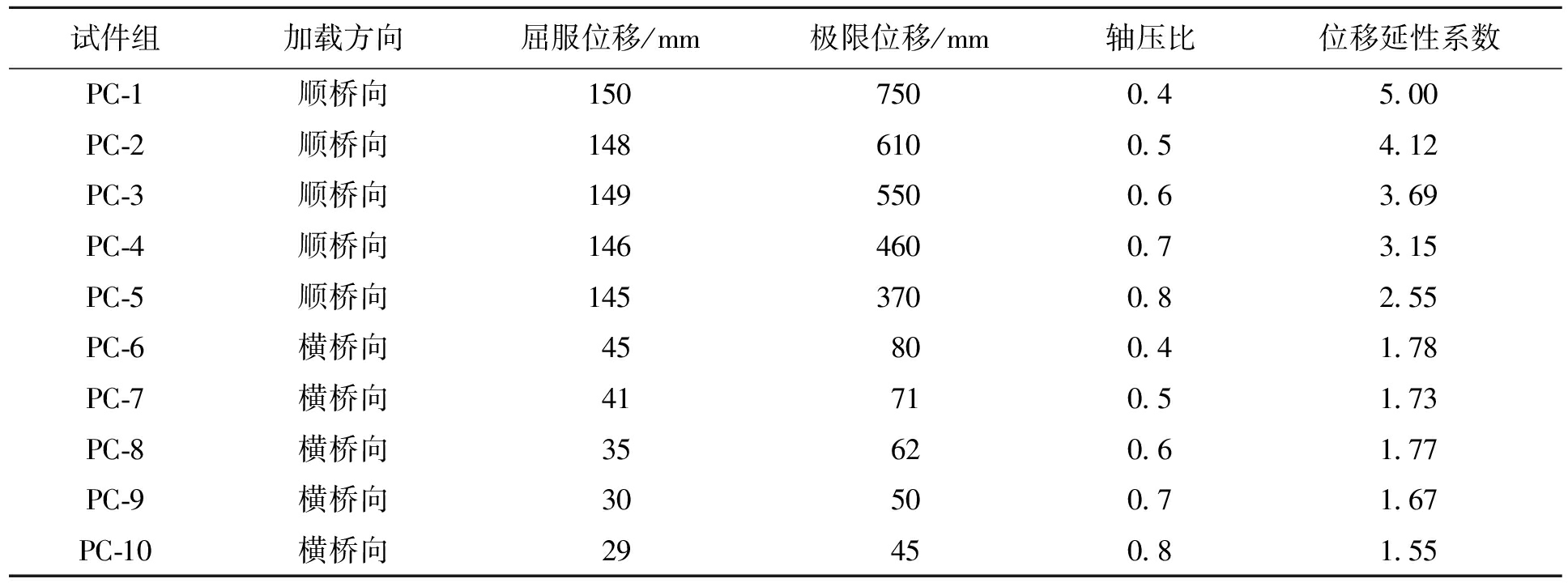
试件组加载方向屈服位移/mm极限位移/mm轴压比位移延性系数PC-1顺桥向1507500.45.00PC-2顺桥向1486100.54.12PC-3顺桥向1495500.63.69PC-4顺桥向1464600.73.15PC-5顺桥向1453700.82.55PC-6横桥向45800.41.78PC-7横桥向41710.51.73PC-8横桥向35620.61.77PC-9横桥向30500.71.67PC-10横桥向29450.81.55
轴压比亦是影响桥墩位移延性的一个重要参数,比较顺桥向和横桥向的加载可以看出顺桥向的屈服位移要大于横桥向的屈服位移,而且顺桥向的屈服位移随轴压比的变化不大,说明弱轴方向容易进入屈服.把PC-1~PC-5和PC-6~PC-10按加载方向分成两类,比较轴压比对其位移延性系数的影响,可以看出,无论是横桥向加载还是顺桥向加载,其位移延性系数都会随着轴压比的增大而减小,说明轴压比越大,构件的位移延性能力越小,反之越好.
3.2 桥墩构件整体耗能能力评估
结构或构件的耗能能力是指在地震作用下结构或构件吸收和消耗地震能量的能力.耗能能力表现为在经历反复塑性变形后结构或构件仍具有一定的承载能力,结构或构件在往复荷载作用下的滞回曲线所围成的面积大小也能代表其耗能能力强弱.为了更好地评估钢筋混凝土Y型桥墩构件的整体耗能性能,选取墩高和轴压比为控制变量来进行对比分析.图6、7分别为轴压比ηk为0.8时不同墩高和墩高H为13 m时不同轴压比的桥墩整体构件的耗能系数曲线.
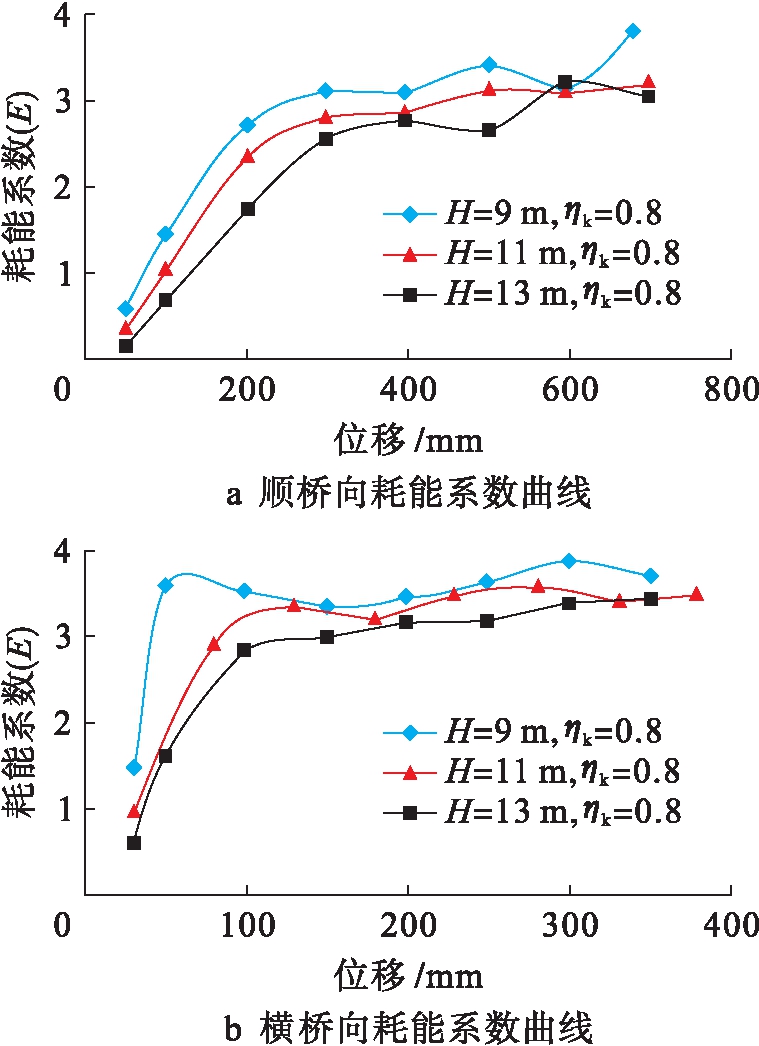
图6 轴压比为0.8时桥墩模型的耗能系数曲线
Fig.6 Energy dissipation coefficient curves of pier model with axial compression ratio of 0.8
从图6、7可以看出,各试件的等效黏滞阻尼系数随着墩顶位移的增加而增大,说明随着桥墩塑性变形的不断发展其耗能能力随之增加.在轴压比相同的情况下,无论是顺桥向加载还是横桥向加载,较矮桥墩具有较高的等效黏滞阻尼系数,说明降低桥墩高度能显著提高桥墩的耗能能力.在墩高相同的情况下,对于顺桥向加载来说,轴压比越小,桥墩的耗能能力越好,但轴压比为0.2和0.4时的耗能能力远远大于轴压比为0.6和0.8的情况,横桥向加载时轴压比的变化对桥墩耗能能力的影响不大.因此,横桥向的耗能能力要大于顺桥向.总体来说,Y型桥墩构件的耗能能力为桥墩越低其耗能能力越强,轴压比在一定范围内减小时其耗能能力显著降低,桥墩在横桥向有着较好的耗能能力.
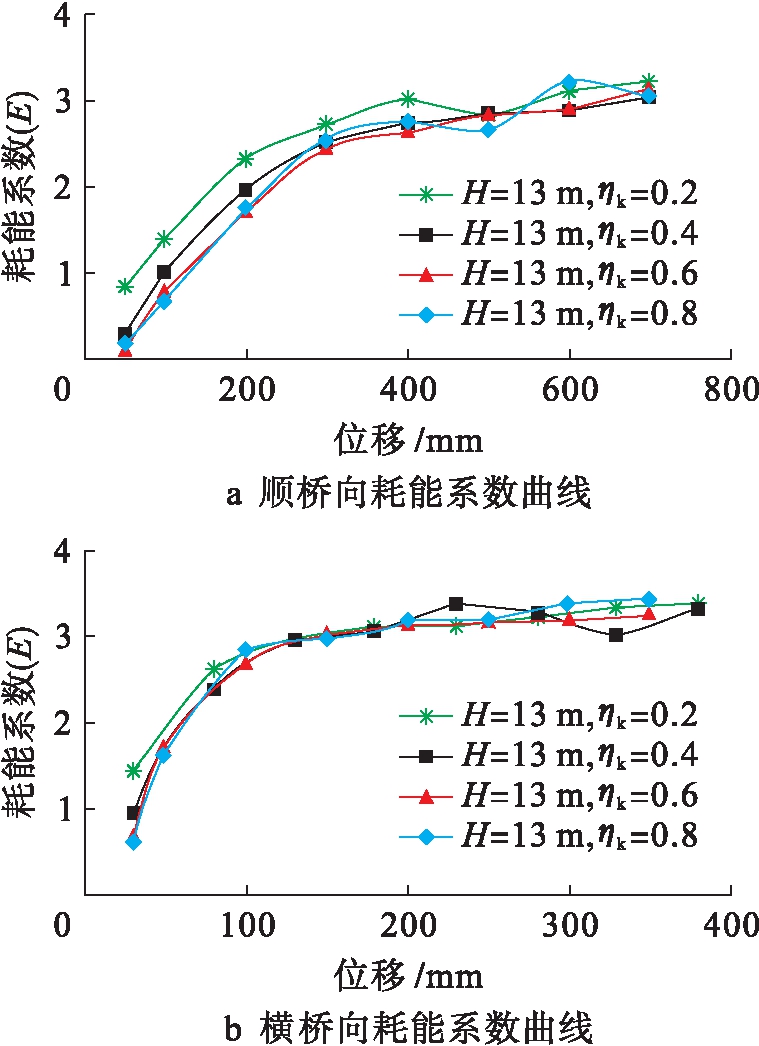
图7 墩高为13 m时桥墩模型的耗能系数曲线
Fig.7 Energy dissipation coefficient curves of pier model with pier height of 13 m
4 结 论
影响桥墩抗震性能的因素有很多,弯矩-曲率曲线反映了构件的受弯性能,对于分析预测其弹塑性变形能力有巨大作用.位移延性系数可以反映出结构或构件的变形能力.对于Y型桥墩分别从截面和构件上进行了评估,可以得出以下结论:
1)对桥墩截面的弯矩-曲率分析可知,轴压比在较小范围内(轴压比小于0.5)时,轴压比增大对桥墩延性能力起着积极影响,而超过一定值(轴压比大于0.5)时,轴压比的增大开始起负面影响.轴压比约为0.5时,桥墩截面的延性能力最好.桥墩截面抗震性能评估公式也验证了合适的轴压比对提高桥墩延性能力至关重要.
2)对Y型桥墩的变形能力而言,轴压比增大,桥墩的屈服位移减小,横桥向加载在29~45 mm内就会达到屈服,其允许的变形量很难抵御强震的作用,受拉区钢筋的屈服和受压区混凝土的压坏是其主要原因.
3)Y型桥墩构件整体的耗能能力为桥墩越低其耗能能力越强,轴压比在一定范围内减小时,其耗能能力显著降低,桥墩在横桥向有较好的耗能能力,但对于横桥向的地震作用,依然存在一些不足,两肢臂的抗剪能力不足以抵抗强震,Y形截面形式导致其横向吸收地震的能力不强.
[1] 李宏男.结构多维抗震理论[M].北京:科学出版社,2006.
(LI Hong-nan.Structure multidimensional seismic theory[M].Beijing:Science Press,2006.)
[2] 范立础.桥梁工程[M].上海:同济大学出版社,2012.
(FAN Li-chu.Bridge engineering[M].Shanghai:Tongji University Press,2012.)
[3] Kwasniewski L.Nonlinear dynamic simulations of collapse for a multistory building[J].Engineering Structures,2010,32:1223-1235.
[4] 于琦,孟少平,吴京.基于变形与能量双重准则的钢筋混凝土结构地震损伤评估[J].土木工程学报,2011,44(5):16-23.
(YU Qi,MENG Shao-ping,WU Jing.Deformation and energy-based seismic damage evaluation of reinforced concrete structures[J].Chinese Journal of Civil Engineering,2011,44(5):16-23.)
[5] 丁阳,伍敏,徐龙河,等.钢柱考虑损伤累积效应的强震下损伤演化规律[J].建筑结构学报,2011,32(7):112-117.
(DING Yang,WU Min,XU Long-he,et al.Seismic damage evolution of steel columns considering da-mage accumulation[J].Journal of Building Structures,2011,32(7):112-117.)
[6] 唐代远,陆新征,叶列平,等.柱轴压比对我国RC框架结构抗地震倒塌能力的影响[J].工程抗震与加固改造,2010,33(5):26-35.
(TANG Dai-yuan,LU Xin-zheng,YE Lie-ping,et al.Influence of axial compression ratio to the seismic collapse resistance of RC frame structures[J].Earthquake Engineering and Reinforcement,2010,33(5):26-35.)
[7] 陆新征,唐代远,叶列平,等.我国7度设防等跨RC框架抗地震倒塌能力研究[J].地震工程与工程振动,2011,31(5):13-20.
(LU Xin-zheng,TANG Dai-yuan,YE Lie-ping,et al.Study on the seismic collapse resistance of RC frame structures with equal spans in zones with seismic in-tensity Ⅶ[J].Earthquake Engineering and Engineering Vibration,2011,31(5):13-20.)
[8] 丁阳,刘碧文,葛金刚.地震作用下单层柱面网壳倒塌机理分析与试验研究[J].地震工程与工程振动,2013,33(2):68-73.
(DING Yang,LIU Bi-wen,GE Jin-gang.Collapse mechanism analysis and experiment study of single-layer cylindrical reticulated shells under earthquake action[J].Earthquake Engineering and Engineering Vibration,2013,33(2):68-73.)
[9] Haselton C B,Liel A B,Deierlein G G,et al.Seismic collapse safety of reinforced concrete buildingsⅠ:assessment of ductile moment frames[J].Journal of Structural Engineering,2010,137(4):481-491.
[10] Liel A B,Haselton C B,Deierlein G G.Seismic collapse safety of reinforced concrete buildings Ⅱ:comparative assessment of nonductile and ductile moment frames[J].Journal of Structural Engineering,2010,137(4):492-502.
[11] Zareian F,Krawinkler H.Structural system parameter selection based on collapse potential of buildings in earthquakes[J].Journal of Structural Engineering,2013,236(8):933-943.